Какими свойствами обладает сумма произведение частное рациональных чисел
1. Сложение рациональных чисел обладает переместительным и сочетательным свойствами.
Иными словами, если a, b и с — любые рациональные числа, то а + b = b + a, а+(b + с) = (а + b) + с.
Прибавление нуля не изменяет числа, а сумма противоположных чисел равна нулю.
Значит, для любого рационального числа имеем: а + 0 = а, а + ( — а)=0.
Умножение рациональных чисел тоже обладает переместительным и сочетательным свойствами. Другими словами, если а, b и с — любые рациональные числа, то ab — ba, a(bc) — (ab)c.
Умножение на 1 не изменяет рационального числа, а произведение числа на обратное ему число равно 1.
Значит, для любого рационального числа а имеем:
Умножение числа на нуль дает в произведении нуль, т. е. для любого рационального числа а имеем:
а • 0 = 0.
Произведение может быть равно нулю лишь в том случае, когда хотя бы один из множителей равен нулю: если а • b = 0, то либо а = 0, либо b = 0 (может случиться, что и а = 0, и b=0).
Умножение рациональных чисел обладает и распределительным свойством относительно сложения. Другими словами, для любых рациональных чисел a, b и с имеем: (a+b)• c = ac+bc.
С рациональными числами люди, как вы знаете, знакомились постепенно. Вначале при счете предметов возникли натуральные числа. На первых порах их было немного. Так, еще недавно у туземцев островов в Торресовом проливе (отделяющем Новую Гвинею от Австралии) были в языке названия только двух чисел: «урапун» (один) и «оказа» (два). Островитяне считали так: «оказа-урапун» (три), «оказа-оказа» (четыре) и т. д. Все числа, начиная с семи, туземцы называли словом, обозначавшим «много».
Ученые полагают, что слово для обозначения сотни появилось более 7000 лет назад, для обозначения тысячи — 6000 лет назад, а 5000 лет тому назад в Древнем Египте и в Древнем Вавилоне появляются названия для громадных чисел — до миллиона. Но долгое время натуральный ряд чисел считался конечным: люди думали, что существует самое большое число.
Величайший древнегреческий математик и физик Архимед (287—212 гг. до н. э.) придумал способ описания громадных чисел. Самое большое число, которое умел называть Архимед, было настолько велико, что для его цифровой записи понадобилась бы лента в две тысячи раз длиннее, чем расстояние от Земли до Солнца.
Но записывать такие громадные числа еще не умели. Это стало возможным только после того, как индийскими математиками в VI в. была придумана цифра нуль и ею стали обозначать отсутствие единиц в разрядах десятичной записи числа.
При разделе добычи и в дальнейшем при измерениях величин, да и в других похожих случаях люди встретились с необходимостью ввести «ломаные числа» — обыкновенные дроби. Действия над дробями еще в средние века считались самой сложной областью математики. До сих пор немцы говорят про человека, попавшего в затруднительное положение, что он «попал в дроби».
Чтобы облегчить действия с дробями, были придуманы десятичные дроби. В Европе их ввел в Х585 г. голландский математик и инженер Симон Стевин.
Отрицательные числа появились позднее, чем дроби. Долгое время такие числа считали «несуществующими», «ложными» прежде всего из-за того, что принятое истолкование для положительных и отрицательных чисел «имущество — долг» приводило к недоумениям: можно сложить или вычесть «имущества» или «долги», но как понимать произведение или частное «имущества» и «долга»?
Однако несмотря на такие сомнения и недоумения, правила умножения и деления положительных и отрицательных чисел были предложены в III в. греческим математиком Диофантом (в виде: «Вычитаемое, умноженное на прибавляемое, дает вычитаемое; вычитаемое на вычитаемое дает прибавляемое» и т. д.), а позже индийский математик Б х а с к а р а (XII в.) выразил те же правила в понятиях «имущество», «долг» («Произведение двух имуществ или двух долгов есть имущество; произведение имущества и долга есть долг». То же правило и при делении).
Было установлено, что свойства действий над отрицательными числами те же, что и над положительными (например, сложение и умножение обладают переместительным свойством). И наконец с начала прошлого века отрицательные числа стали равоправными с положительными.
В дальнейшем в математике появились новые числа — иррациональные, комплексные и другие. О них вы узнаете в старших классах.
Источник
Ниже рассмотрим правила основных математических действий над рациональными числами: сложение, вычитание, умножение и деление. Разберем теорию на практических примерах.
Действие сложения рациональных чисел
Рациональные числа содержат натуральные, тогда смысл действия сложения рациональных чисел сопоставим со смыслом сложения натуральных. Например, сумму рациональных чисел, записанную как 5+1 4возможно описать следующим образом: к 5 целым предметам добавили четверть такого предмета, после чего полученное количество рассматривается совместно.
Сформулируем правила сложения рациональных чисел:
Сложение нуля с отличным от него рациональным числом
Определение 1
Прибавление нуля к любому числу дает то же число. Данное правило возможно записать в виде равенства:a + 0 = a (для любого рационального числа а). Используя переместительное свойство сложения, получим также верное равенство: 0 + a = a.
Пара простых примеров: сумма рационального числа 2,1 и числа 0 равно 2,1 и: 645+0 = 645.
Сложение противоположных рациональных чисел
Определение 2
Сумма противоположных чисел равна нулю.
Данное правило можно записать в виде: a+(-a)=0 (для любого рационального числа a).
К примеру, числа 45,13 и -45,13 являются противоположными, т.е. их сумма равно нулю: 45,13+(-45,13) = 0.
Сложение положительных рациональных чисел
В виде обыкновенной дроби возможно представить любое положительное рациональное число и использовать далее схему сложения обыкновенных дробей.
Пример 1
Необходимо произвести сложение рациональных чисел: 0,6 и 59.
Решение
Выполним перевод десятичной дроби в обыкновенную и тогда: 0,6 + 59 = 610 + 59.
Осуществим сложение дробей с разными знаменателями:
610+59= 5490+ 5090= 10490=1745
Ответ: 0,6 + 59= 1745.
Рациональные числа, которые подвергают действию сложения, возможно записать в виде конечных десятичных дробей или в виде смешанных чисел и, таким образом, осуществить сложение десятичных дробей и смешанных чисел соответственно.
Сложение рациональных чисел с разными знаками
Определение 3
Для того, чтобы осуществить сложение рациональных чисел с разными знаками, необходимо из бОльшего модуля слагаемых вычесть меньший и перед полученным результатом поставить знак того числа, модуль которого больше.
Пример 2
Необходимо осуществить сложение рациональных чисел с разными знаками 8,2 и -234 .
Решение
Согласно исходным данным, необходимо произвести сложение положительного числа с отрицательным. Придерживаясь вышеуказанного правила, определим модули заданных чисел: |8,2| = 8,2 и|-234|=234. Проведя сравнение модулей – рациональных чисел, получим: 8,2 > 234 и соответственно поймем, какое число из заданных станет уменьшаемым, а какое – вычитаемым. Произведем вычитание смешанных чисел, т.е.: 8,2-234= 8210- 234= 59 20.
Полученному результату присваивается знак плюс, т.к. бОльшее из слагаемых по модулю – положительное число. Ответ: 8,2 +(-234)= 5920.
Сложение отрицательных рациональных чисел
Определение 4
Для того, чтобы произвести сложение отрицательных рациональных чисел, необходимо сложить модули заданных слагаемых, затем полученному результату присвоить знак минус.
Пример 3
Необходимо произвести сложение чисел: -4,0203 и -12,193.
Решение
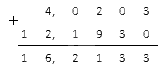
Модули заданных чисел соответственно равны: 4,0203 и 12,193. Сложим их:

Полученному результату присваиваем знак минус: -16,2133.
Ответ: (-4,0203)+(-12,193) =-16,2133.
Действие вычитания рациональных чисел
Вычитание – действие, обратное сложению, в котором мы находим неизвестное слагаемое по сумме и известному слагаемому. Тогда из равенства c+b=a следует, чтоa-b=cи a-c=b. И наоборот: из равенств a-b =c и a-c=bследует, что c+b=a.
Определение 5
При вычитании из бОльшего положительного рационального числа мы либо производим вычитание обыкновенных дробей, либо, если это уместно, вычитание десятичных дробей или смешанных.
Пример 4
Необходимо вычислить разность рациональных чисел: 4,(36)– 15.
Решение
Сначала переведем периодическую десятичную дробь в обыкновенную: 4,(36) = 4+(0,36 + 0,0036 +…)= 4+0,361-0,01=4 + 3699=4+ 411= 4411
Далее переходим к действию вычитания обыкновенной дроби из смешанного числа: 4, (36)-15= 4411- 15=4 + 411-15=4+2055- 1155=4+955=4955
Ответ: 4,(36)-15= 4955
Определение 6
В прочих случаях вычитание рациональных чисел необходимо заменить сложением: к уменьшаемому прибавить число, противоположное вычитаемому:a–b=a+(-b).
Указанное равенство можно доказать, опираясь на свойства действий с рациональными числами. Они дают возможность записать цепочку равенств: (a+(-b))+b=a+((-b)+b)=a+0=a. Отсюда в силу смысла действия вычитания следует, что сумма a+(-b) есть разность чисел a и b.
Пример 5
Необходимо из рационального числа 27 вычесть рациональное число 537
Решение
Согласно последнему указанному правилу используем для дальнейших действий число, противоположное вычитаемому, т.е. -537. Тогда: 27-537=27+-537
Далее произведем сложение рациональных чисел с разными знаками: 27+-537=-537-27=-537-27= -517
Ответ:27+-537=-517
Действие умножения рациональных чисел
Общее понятие числа расширяется от натуральных чисел к целым, так же как от целых к рациональным. Все действия с целыми числами имеют те же свойства, что и действия с натуральными. В таком случае, и действия с рациональными числами также должны характеризоваться всеми свойствами действий с целыми числами. Но для действия умножения рациональных чисел присуще дополнительное свойство: свойство умножения взаимообратных чисел. Вышесказанному соответствуют все правила умножения рациональных чисел. Укажем их.
Умножение на нуль
Определение 7
Произведение любого рационального числа a на нуль есть нуль.
Т.е. a·0=0.
Используя переместительное свойство умножения, получим: 0·а=0.
К примеру, умножение рационального числа 713 на 0 даст 0. Перемножив отрицательное рациональное число -718и нуль, также получим нуль. В частном случае, произведение нуля на нуль есть нуль: 0·0=0.
Умножение на единицу
Определение 8
Умножение любого рационального числа a на 1 дает число a.
Т.е. a·1=a или 1 · a = a (для любого рационального a). Единица здесь является нейтральным числом по умножению.
К примеру, умножение рационального числа 5,46 на 1 даст в итоге число 5,46.
Умножение взаимообратных чисел
Определение 9
Если множители есть взаимообратные числа, то результатом их произведения будет единица. Т.е. : а·а-1=1.
К примеру, результатом произведения чисел 56 и 65 будет единица.
Умножение положительных рациональных чисел
В общих случаях умножение положительных рациональных чисел сводится к умножению обыкновенных дробей. Первым действием множители представляются в виде обыкновенных дробей, если заданные числа таковыми не являются.
Пример 6
Необходимо вычислить произведение положительных рациональных чисел 0,5 и 625.
Решение
Представим заданную десятичную дробь в виде обыкновенной 0,5 = 510= 12.
Далее произведем умножение обыкновенных дробей: 12 · 625= 650= 325.
Ответ: 0,5 ·625= 325
Можно также работать и с конечными десятичными дробями. Удобнее будет в данном случае не переходить к действиям над обыкновенными дробями.
Пример 7
Необходимо вычислить произведение рациональных чисел 2,121 и 3,4.
Решение
Перемножим десятичные дроби столбиком:
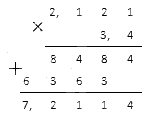
Ответ: 2,121 · 3,4 = 7,2114
В частных случаях нахождение произведения рациональных чисел представляет собой умножение натуральных чисел, умножение натурального числа на обыкновенную или десятичную дробь.
Умножение рациональных чисел с разными знаками
Определение 10
Чтобы найти произведение рациональных чисел с разными знаками, необходимо перемножить модули множителей и полученному результату присвоить знак минус.
Пример 8
Необходимо найти произведение чисел: -338и 212
Решение
Согласно вышеуказанному правилу получим: -338·212=-338·212=-338·212
Заменим смешанные дроби неправильными и найдем искомое произведение: -338·212=-278·52=-13516=-8716
Ответ: -338·212=-8716
Умножение отрицательных рациональных чисел
Определение 11
Для того, чтобы найти произведение отрицательных рациональных чисел, необходимо перемножить модули множителей.
Пример 9
Необходимо найти произведение отрицательных рациональных чисел -3,146 и -56.
Решение: модули заданных чисел соответственно равны 3,146 и 56.
Перемножим их столбиком:
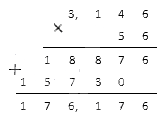
Полученный результат и будет являться искомым произведением.
Ответ: (-3,146) · (-56) = 176,176
Деление рациональных чисел
Деление – действие, обратно умножению, в ходе которого мы находим неизвестный множитель по заданному произведению и известному множителю. Смысл действия деления можно записать так: из равенстваb·c =a следует, что a:b =c и a:c=b. И наоборот: из равенств a:b=c и a:c=b следует, чтоb·c=a.
На множестве рациональных чисел деление не считается самостоятельным действием, поскольку оно производится через действие умножения. Собственно, этот смысл заложен в правило деления рациональных чисел.
Определение 12
Разделить число а на число b, отличное от нуля – то же самое, что умножить число a на число, обратное делителю. Т.е., на множестве рациональных чисел верно равенство: a:b=a·b-1.
Указанное равенство доказывается просто: на основе свойств действий с рациональными числами справедливой будет цепочка равенств (a·b-1)· b=a·(b-1·b)=a·1=a, которая и доказывает равенство a : b = a · b-1.
Таким образом, деление рационального числа на другое рациональное число, отличное от нуля, сводится к действию умножения рациональных чисел.
Пример 10
Необходимо выполнить действие деления 313:-116
Решение
Определим число, обратное заданному делителю. Запишем заданный делитель в виде неправильной дроби: -116= -76.
Число, обратное этой дроби, будет: -67. Теперь, согласно вышеуказанному правилу, произведем действие умножения рациональных чисел: 313-116=313·-67=103·(-67) =-(103·67)=-207= -267
Ответ: 313:-116=-267
Источник
