Какими свойствами обладает сумма

Отношение равенства является отношением эквивалентности на множестве дробей, поэтому оно порождает на нём классы эквивалентности. В каждом таком классе содержатся равное между собой дроби. Например, множество дробей {, , , , …} – это один класс, множество дробей {, , , , …} – это другой класс и т.д.
Дроби одного класса выражают длину одного и того же отрезка. Но длина отрезка должна представляться единственным числом. Поэтому считают, что равные дроби – это различные записи одного и того же положительного рационального числа.
Положительным рациональным числом называется класс дробей, а каждая дробь, принадлежащая этому классу, есть запись (представление) этого числа.
Например, о дроби мы должны говорить, что она является записью некоторого рационального числа. Однако часто для краткости говорят: – это рациональное число.
Множество всех положительных рациональных чисел принято обозначать символом Q+. Определим на это множество отношение равенства.
Если положительное рациональное число a представить дробью , а положительное рациональное число b – другой дробью , то a = b тогда и только тогда, когда mq=np.
Из данного определения следует, что равные рациональные числа представляются равными дробями. Среди всех записей любого положительного рационального числа выделяют дробь, которая является несократимой, и доказывают, что любое рациональное число представимо единственным образом несократимой дробью (мы это доказательство опускаем). Для того чтобы рациональное число представить несократимой дробью, достаточно числитель m и знаменатель n разделить на их наибольший общий делитель.
Выяснить теперь, как определяются арифметические действия с положительными рациональными числами.
Пусть при некотором единственном отрезке e длина отрезка x выражается дробью , а длина отрезка у – дробью , и пусть отрезок z состоит из отрезков x и y. Такая n-ая часть отрезка e укладывается в отрезок z m+p раз, т.е. длина отрезка z выражается дробью . Поэтому полагают, что .
Если положительное рациональное число a представить дробью , а положительное рациональное число b – дробью , то их суммой называется число a+b, которое представляется дробью .
Таким образом по определению
. (1)
Можно доказать, что при замене дробей и , представляющих числа а и b, равными им дробями, дробь заменяется равной ей дробью. Поэтому сумма рациональных чисел не зависит от выбора представляющих их дробей.
В определении суммы рациональных чисел мы использовали их представления в виде дробей с одинаковыми знаменателями. Если же числа а и b представлены дробями с различными знаменателями, то сначала надо привести их к одному знаменателю, а затем применить правило (1).
Сложение положительных рациональных чисел коммутативно и ассоциативно,
( Q+) a + b = b + a;
( Q+) (a + b) + c = a + (b + c).
Докажем, например, коммутативность сложения. Представим числа а и b дробями и . Тогда сумма a+b представляется дробью , а сумма b+a – дробью . Так как m, p, n – натуральные числа, то m+p = p+m и, следовательно, a+b = b+a. Таким образом, коммутативность сложения положительных рациональных чисел вытекает из коммутативности сложения натуральных чисел.
Если положительное числа а представлено дробью , а положительное рациональное число b – дробью , то их произведением называется число ab, которое представляет дробью .
Такимобразом, по определению,
. (2)
Можно доказать, что при замене дробей и , представляющих числа a и b, равными им дробями, дробь заменяется равной ей дробью. Поэтому произведение чисел a и b не зависит от выбора представляющих их дробей.
Умножение положительных рациональных чисел коммутативно, ассоциативно и дистрибутивно относительно сложения и вычитания. Доказательство этих свойств основывается на определении умножения исложения положительных рациональных чисел, а также на соответствующих свойствах сложения и умножения натуральных чисел.
Определение сложения положительных рациональных чисел дает возможность определить отношение «меньше» на множестве Q+.
Пусть a и b – положительные рациональные числа. Считают, что число b меньше числа а, если существует такое положительное рациональное число с, что а =b + с.
В этом же случае считают, что число а больше числа b. Пишут b < a,
a >b.
Так определенное отношение «меньше» обладает рядом свойств, которые мы приводим без доказательства.
1. Отношение «меньше» на множестве Q+ антисимметрично и транзитивно, т.е. является отношением порядка, а множество Q+ упорядоченным множеством.
2. Если рациональные числа a и b представлены дробями и (т.е. дробями, имеющими одинаковые знаменатели), то a <b в том и только в том случае, когда m < p.
3. Если рациональные числа aи bпредставлены дробями и (т.е. дробями, имеющими разные знаменатели), то a < b в том и только в том случае, когда mq < пр.
4. Во множестве положительных рациональных чисел нет наименьшего числа.
5. Между любыми двумя различными числами а и b из Q+ заключено бесконечно много чисел этого же множества. Это свойство называют свойством плотности множества Q+.
6. Во множестве положительных рациональных чисел нет наибольшего числа.
Вычитание положительных рациональных чисел определяется как операция, обратная сложению, т.е. это такая операция, которая удовлетворяет условию: a – b = c тогда и только тогда, когда a = b + c.
Разность а – b положительных рациональных чисел существует тогда и только тогда, когда b < а. Если разность а – b существует, то она единственна.
Используя определение и условие существования разности, можно получить правило вычитания положительных рациональных чисел, представленных дробями и , где т < р:
(3)
Деление положительных рациональных чисел определяется как операция, обратная умножению, т.е. это такая операция, которая удовлетворяет условию: тогда и только тогда, когда .
Из этого определения и правила нахождения произведения положительных рациональных чисел можно получить правило деления положительных рациональных чисел, представленных дробями и :
. (4)
Из этого правила следует, что частное положительных рациональных чисел всегда существует.
Источник
Ниже приведены характеристики чисел с примерами, которые рассматривает сайт aboutnumber.ru
Сумма цифр
Сумма цифр, из которых состоит число.
62316 → 6 + 2 + 3 + 1 = 18
Произведение цифр
Произведение цифр, из которых состоит число.
872 → 8 * 7 * 2 = 112
Количество цифр в числе
Отображение количества цифр в числе (если их больше 4-х). Это удобно, так как не всегда можно на глаз определить
порядок числа.
57348920572348 → 14
Все делители числа
Полный список делителей, на которые делится число без остатка.
2612 → 1, 2, 4, 653, 1306, 2612
Наибольший делитель из ряда степеней двойки
Ряд степеней двойки — это ряд вида 1, 2, 4, 8, 16, 32, 64, 128, 256 и т.д.
Эти числа являются основными числами в бинарной математике (в двоичной записи), так как ими можно охарактеризовать
объем
информации.
832 → 64
Количество делителей
Суммарное число делителей.
3638143886 → всего 32 делителя
Сумма делителей
Сумма всех делителей числа.
77432243032 → сумма делителей 145185455700
Простое число
Проверка на простое число. Простое число — это число, которое делится без остатка только на единицу и само себя.
Таким образом у простого числа может быть всего два делителя.
677 → 1 * 677
Полупростое число
Проверка на полупростое число. Полупростое число — число, которое можно представить в виде произведения двух простых чисел.
У полупростого числа два делителя — оба простые числа.
898 → 2 * 449
Обратное число
Два числа называются обратными если их произведение равно единице. Таким образом обратным к заданному числу N всегда
будет 1/N.
125 → 0.008
Проверка: 0.008 * 125 = 1
Факторизация
Факторизация числа — представление числа в виде произведения простых чисел.
220683351 → 3 * 7 * 953 * 11027
Двоичный вид
Двоичное, оно же бинарное представление числа. Это запись числа в системе счисления с основанием два.
72412810 → 101100001100101000002
Троичный вид
Троичное представление числа. Это запись числа в системе счисления с основанием три.
990418010 → 2001220112221113
Восьмеричный вид
Восьмеричное представление числа. Это запись числа в системе счисления с основанием восемь.
9788143604410 → 13312140276148
Шестнадцатеричный вид (HEX)
Шестнадцатеричное представление числа. Часто его пишут английскими буквами «HEX». Это запись числа в системе
счисления с основанием шестнадцать.
12444510 → 1E61D16
Перевод из байтов
Конвертация из байтов в килобайты, мегабайты, гигабайты и терабайты.
29141537 (байт) → 27 мегабайтов 810 килобайтов 545 байтов
Цвет
В случаем, если число меньше чем 16777216, то его можно представить в виде цвета. Шестнадцать миллионов цветов,
которые можно
закодировать стандартной цветовой схемой компьютера.
8293836 →
RGB(126, 141, 204) или #7E8DCC
Наибольшая цифра в числе (возможное основание)
Наибольшая цифра, встречающаяся в числе. В скобках указана система счисления, с помощью которой, возможно, записано
это число.
347524172 → 7 (8, восьмеричный вид)
Перевод двоичной/троичной/восьмеричной записи в десятичную
Число, записанное с помощью единиц и нолей — имеет бинарный вид, таким образом его можно перевести в
десятичную систему счисления.
Число, записанное с помощью единиц, нолей и двоек — имеет троичный вид.
Если с помощью цифр до семи (включая) — восьмеричный вид числа.
111010010010112 → 1492310
120201001200213 → 278227610
745312768 → 1590547010
Число Фибоначчи
Проверка на число Фибоначчи. Числа Фибоначчи — это последовательно чисел, в которых каждый последующий элемент равен
сумме двух предыдущих.
Ряд Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д.
Позиция в ряду Фиббоначчи
Характеризует порядковый номер числа в ряду Фибоначчи.
21 → 8-е число в ряду Фибоначчи
Нумерологическое значение
Нумерологическое значение вычисляется путем последовательного сложения всех цифр числа до тех пор, пока не
не получится цифра от 0 до 9. В нумерологии каждой цифре соответствует свой характер.
8372890 → 8 + 3 + 7 + 2 + 8 + 9 + 0 = 37 → 3 + 7 = 10 → 1 + 0 = 1
мужество, логика, независимость, самостоятельность, индивидуализм, смелость, решительность, изобретательность
Синус числа
Расчет тригонометрической функции синуса числа в радианах.
Sin(18228730686) = -0.20084127807633853
Косинус числа
Расчет тригонометрической функции косинуса числа в радианах.
Cos(792834113) = 0.6573990013186783
Тангенс числа
Расчет тригонометрической функции тангенса числа в радианах. Чтобы получить котангенс числа, надо единицу поделить на
величину тангенса.
Tan(651946045) = 2.5709703278560982
Натуральный логарифм
Это логарифм числа по основанию константы e ≅ 2,718281828459.
Ln(7788338399) = 22.77589337484777
Десятичный логарифм
Это логарифм числа по основания десять.
LOG(1010432) = 6.004507091707365
Квадратный корень
Квадратный корень из введенного числа.
8512326 → 2917.589073190397
Кубический корень
Кубический корень из введенного числа.
5834788 → 180.02867855810877
Квадрат числа
Число, возведенное в квадрат, то есть умноженное само на себя.
31203^2 = 973627209
Перевод из секунд
Конвертация числа секунд в дни, часы, минуты и секунды.
1805506 (секунд) → 2 недели 6 дней 21 час 31 минута 46 секунд
Дата по UNIX-времени
UNIX-время или UNIX-дата — количество секунд, прошедших с полуночи 1 января 1970 года (по UTC).
Таким образом введенное число можно преобразовать в дату.
5265079917115 → Sun, 04 Nov 2136 10:11:57 GMT
Римская запись
Римская запись числа, в том случае, если оно меньше чем максимальное для римской записи 3999.
2014 → MMXIV
Индо-арабское написание
Запись числа с помощью индо-арабских цифр. Они используются в арабских странах Азии и в Египте.
24579540882896 → ٢٤٥٧٩٥٤٠٨٨٢٨٩٦
Азбука морзе
Число, закодированное с помощью азбуки морзе, каждый символ которой представляется в виде последовательсти
коротких (точка) и длинных (тире) сигналов.
7282077 → –… ..— —.. ..— —– –… –…
MD5
Хэш-сумма числа, рассчитанная по алгоритму MD5.
4706204202547 → db2766a5747fd3f8c8c77a1ddd2e24d0
SHA1
Хэш-сумма числа, рассчитанная по алгоритму SHA-1.
345297 → 3855120d2f9d556544bbd24746d0877b79a023df
Base64
Представление числа в системе Base64, то есть в системе счисления с основанием 64.
78868 → SmF2YVNjcmlwdA==
QR-код числа
Двумерный штрих-код-картинка. В ней зашифровано введенное число.
969393779 →
Источник
Учебник-собеседник 5 кл. авт. Шеврин Л.Н., Гейн
А.Г., Коряков И.О., Волков М.В.
Цель урока: познакомить учащихся со
свойствами числа 1.
Задачи урока:
Обучающие:
- Обобщить знания учащихся о свойствах единицы.
- Получить свойство: “Степень числа 1”
- Выяснить вопрос: “Чему равно частное 1:а?”
Развивающие:
- Формировать навыки работы с книгой,
вычислительные навыки. - Формировать умения анализа и обобщения
математических высказываний; - Работать над развитием устной математической
речи.
Воспитательные: Воспитывать интерес к
урокам математики через межпредметные связи с
литературой.
Ход урока
Слово учителя: “Обратите внимание на
слова древнегреческого драматурга Эсхила,
взятые в качестве эпиграфа урока:
“Послушайте, что смертным сделал я – число им
изобрел”.
Сегодня на уроке вспомним все изученные
свойства единицы, еще узнаем что-то новое про
единицу, увидим, какое большое значение имеет
единица в математике.
Верно сказано:
“Твой ум без числа ничего не постигает”. И вы
докажете это на уроке.
План урока:
1. Работа по учебнику-собеседнику.
2. Обсуждение вопросов.
3. Устная работа
4. Введение свойства степени 1.
5. Работа в тетради.
6. Рефлексия урока.
Работаем по учебнику-собеседнику. Разбираем
самостоятельно урок 21. Читаем до первого
звоночка. Ваша задача: познакомиться с вопросами,
ответить на них. Обсуждаем прочитанное, затем вы
читаете далее.
Итак, стр.75, урок 21. Вопросы 1-2.
Обсуждение вопросов:
1. Чем знаменательно число единица в
натуральном ряду?
Ответ: С него начинается натуральный ряд.
2. Какие числа называем натуральными?
Ответ: Числа, которыми пользуемся для пересчета
предметов.
3. Каким свойством обладает число 1 при сложении?
При вычитании?
Ответ: Если к натуральному числу прибавить
единицу, то получится следующее натуральное
число: n+1.Применяя многократно действие сложения
числа 1, можно получить любое натуральное число.
Натуральный ряд бесконечен. Если из натурального
числа вычесть 1, то получится предыдущее число.
Существует ли самое маленькое число? А самое
большое натуральное число? Назовите последующее
и предыдущее числа 5178.
Далее читаете до второго звоночка материал
параграфа.
Обсуждение вопросов:
1. Каким свойством обладает число 1 при
умножении?
Ответ: Если один из множителей равен 1, то
произведение равно другому множителю.
а * 1=а , 1 * а = а
Что получится, если данное число разделить на 1?
а : 1= а. Доказать.
А если данное число разделить на себя?
Поработаем устно.
- 1+1 * 1-1:1+(1+1-1):1-1(1+1)
- 3208:3208 * 5628:5628
- 317 * 1+233:1
- (657-656) * 49-36
- 4506 * 0+6473:1
- 7218:7218+999 * 1
- 634:(1000-999)+66
Все ли действия мы с вами вспомнили? Существует
ещё одно свойство единицы. Послушайте мою сказку
и сформулируйте его.
Сказка.
Много лет прослужила Единица без единого
замечания, и нужно же было как-то отметить её
заслуги! Поэтому 1 решили возвести в степень.
Сначала возвели во вторую степень. Думали этим и
ограничиться, но опять Единица служит прилежно, а
замечаний хоть бы одно! Возвели 1 в третью
степень. И опять ни одного замечания. Возвели в
четвертую, ни одного замечания! Подумать только!
Возвели в 5-ю, в 6-ю, в 10-ю, в 100-ю. Нет замечаний!
Далеко пошла Единица. Теперь она Единица в 1000-ой
степени. А что изменилось от этого? Ничего –
ровным счетом. Ведь Единица в 1000=ой степени – та же
Единица. И на 1000-ю долю не больше!
1. А теперь сформулируйте ещё одно свойство
единицы.
Ответ: возведение в степень.
2. Что получим, если 1 возведем в любую степень?
Ответ: единица. Докажите.
3. А если любое число возвести в 1 степень?
Ответ: данное число. Докажите.
4. Вычислите устно (12000+ 1991) * 10
Работаем в тетради.
Выполняем задания:
1) Пользуясь тремя пятерками и какими угодно
знаками математических действий, напишите
выражение равное 1.
2) Между некоторыми цифрами 12345 поставьте знаки
действия и скобки так, чтобы получилась 1.
3) Из четырех двоек и любых знаков действия и
скобок напишите выражение, равное 1.
Рефлексия урока:
- Что нового узнали на уроке?
- Чему научились?
- Какими свойствами обладает единица?
Итог урока. Число 1 в математике играет, как
мы убедились, большую роль. Мы с вами разобрали
его свойства при действиях сложения, вычитания,
умножения, деления, возведения в степень, но не
ответили на вопрос: Чему равно частное 1:а?
Домашнее задание: Урок №21, №218(в; г),
сочинить математическую сказку, героем которой
может быть любое число или действие с числами.
Попытайтесь найти ответ на вопрос: “Чему равно
частное 1:а?”, пользуясь математическими
справочниками.
Источник
Таблица
2.2
Варианты задания
4
Вариант | | |
1 | Множество студентов ВУЗа | |
2 | Множество окружностей на плоскости | |
3 | Жители страны на начало этого года | |
4 | Жители страны на начало этого года | |
5 | Прямые в пространстве | |
6 | | |
7 | | |
8 | Читатели библиотеки вашего ВУЗа | |
9 | Множество теннисистов турнира, в | |
1)
Отношение
![]() не
не
является рефлексивным, так как не может
обыграть сам себя.
2)
Отношение
![]() является
является
антирефлексивным, так как каждый
теннисист не обыграл сам себя (не
выполняется рефлексивность).
3) Отношение
![]() не
не
является симметричным, так как найдется
пара теннисистов
![]() и
и![]() такая,
такая,
что![]() обыграл
обыграл![]() по
по
очкам в личных встречах, а![]() не
не
обыграл![]() .
.
4) Отношение
![]() является
является
антисимметричным, так как если
![]() обыграл
обыграл![]() ,
,
то![]() обязательно
обязательно
не обыграл![]() (не выполняется симметричность).
(не выполняется симметричность).
5) Отношение
![]() не
не
является транзитивным, так как может
сложиться ситуация, когда
![]() обыграл
обыграл![]() ,
,![]() обыграл
обыграл![]() ,
,
и в то же время![]() обыграл
обыграл![]() .
.
6) Отношение
![]() является
является
связным, так как любая пара спортсменов
должна сыграть между собой и выявить
победителя.
2. Построим на
конечном множестве отношение, обладающее
таким же набором
свойств, что и данное.
Пусть конечное
множество равно
![]() ,
,
а отношение![]() .
.
Изобразим это отношение в виде графа
(рис. 2. 8).
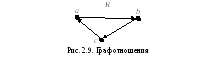
1) Это отношение не является рефлексивным, так как.
2) Отношение
антирефлексивно, так как
![]() ,
,![]() ,
,![]() .
.
3) Отношение не
симметрично, так как
![]() и
и![]() .
.
4) Отношение
антисимметрично, так как
![]() и
и![]() ,
,![]() и
и![]() ,
,![]() и
и![]() .
.
5) Отношение не
транзитивно, так как
![]() и
и![]() но
но![]() .
.
6) Отношение связно,
так как любая пара различных элементов
из множества
![]() вступает
вступает
в отношение
![]() в том или
в том или
ином порядке.
3.
Построим на бесконечном множестве
отношение, обладающее
набором свойств, противоположным
исходному, то есть рефлексивное и не
антирефлексивное, симметричное и не
антисимметричное, транзитивное и не
связное.
Пусть
![]() ,
,
и отношение![]() означает,
означает,
что![]() и
и![]() имеют
имеют
одинаковую дробную часть. Тогда это
отношение будет обладать следующими
свойствами.
1. Отношение
рефлексивно, так как любое число имеет
одинаковую дробную часть само с собой.
2. Отношение
не антирефлексивно, так как найдется
число, например, 2,34, имеющее одинаковую
дробную часть само с собой.
3.
Отношение
симметрично, так как если
![]() и
и![]() имеют
имеют
одинаковую дробную часть, то![]() и
и![]() также
также
имеют одинаковую дробную часть.
4. Отношение
![]() не
не
антисимметрично, так как, например,
числа 2,35 и 3,35 не равны, и в то же время
они находятся в отношении 2, 35![]() 3,
3,
35 и 3,35![]() 2,35.
2,35.
5. Отношение
является транзитивным, так как если
![]() и
и![]() имеют
имеют
одинаковую дробную часть,![]() и
и![]() имеют одинаковую дробную часть, то
имеют одинаковую дробную часть, то![]() и
и![]() также
также
имеют ту же самую дробную часть.
6.
Отношение не связно, так как, например,
числа 3,1 и 1,6 не равны, но
![]() и
и
![]() .
.
Это
отношение рефлексивно, симметрично и
транзитивно, значит, оно является
отношение эквивалентности.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
