Какими свойствами обладает статический момент
Меню сайта
Расчет геометрических характеристик сечений он-лайн NEW – считает любые сечения (сложные). Определяет: площадь сечения, моменты инерции, моменты сопротивления.
Расчет балок на прочность он-лайн – построение эпюр Mx, Qy, нахождение максимального изгибающего момента Mx, максимальной
сдвигающей силы Qy, расчет прогибов, подбор профиля и др. Все просто, все он-лайн.
+ Полное расписанное решение!
Теперь и для статически неопределимых балок!
Расчет рам, ферм балок он-лайн NEW – эпюры Q, M, N, перемещения узлов. Удобный графический интерфейс. Считает любые схемы.
Лекции – теория, практика, задачи…
Примеры решения задач
Справочная информация – ГОСТы, сортамент проката, свойства материалов и другое.
Программы по сопромату (построение эпюр, различные калькуляторы, шпоры и другое).
Форум сопромата и механики
Книги – разная литература по теме.
Заказать задачу
Друзья сайта (ссылки)
WIKIbetta
Разработчикам (сотрудничество)
Веб-мастерам (партнёрка)
О проекте, контакты
Подпроекты
Базовый курс лекций по сопромату, теория, практика, задачи.
::Оглавление::
:: Посмотреть новый вариант этой лекции::
:: Пример расчета ::
:: Расчет характеристик он-лайн (программа) ::
1. Геометрические характеристики сечений.
1.1. Статический момент сечения.
При дальнейшем изучении вопросов прочности, жесткости и устойчивости нам придется иметь дело с некоторыми геометрическими характеристиками сечения: статическими моментами, моментами инерции, моментами сопротивления.
Статическим моментом Sx сечения (фигуры) относительно какой-либо оси х (рис.1.1) называется геометрическая характеристика, определяемая интегралом вида
(1.1)
где y – расстояние от элементарной площадки dA до оси x.
Единицей измерения статического момента является единица длины в третьей степени, обычно см3(см в третьей степени). Статический момент может быть положительным, отрицательным и, в частности, равным нулю. Если отождествить площадь с силой, действующей перпендикулярно плоскости чертежа, то интеграл (4.1) можно рассматривать как сумму моментов сил относительно оси х. По известной из теоретической механике теореме о моменте равнодействующей можно написать
(1.2)
где А – площадь всей фигуры (равнодействующая); ус – расстояние от центра тяжести фигуры до оси х.
Из формулы (1.2) следует формула определения ординаты центра тяжести
ус = Sx/A. (1.3)
Аналогично, статический момент относительно оси у равен
(1.4)
Откуда
xс = Sy/A. (1.5)
Центр тяжести обладает тем свойством, что если тело опереть в этой точке, то оно будет находиться в равновесии.
Из формулы (1.2) и (1.4) следует, что если оси х и у проходят через центр тяжести фигуры, то статический момент относительно этих осей равен нулю. Такие оси называются центральными осями.
Если фигуру можно представить в виде отдельных простых фигур (квадратов, треугольников и т.д.), для которых известны положения центров тяжести, то в этом случае статический момент всей фигуры можно получить как сумму статических моментов этих простых фигурю Это непостредственно следует из свойств определенного интеграла.
Если фигура имеент ось симметрии, то последняя всегда проходит через центр тяжести фигуры, а потому статический момент фигуры относительно оси симметрии всегда равен нулю.
Во многих случаях вместо простых интегралов вида (1.1) и (1.4) удобнее иметь дело с двойными интегралами вида:
(1.1a)
(1.4a)
Здесь D – облать интегрирования.
Пример 1.1. Определить положение центра тяжести сечения, показанного на рис. 1.2, а.
Решение. Разбиваем сечение на два прямоугольника. Проводим вспомогательные оси х и у.
По формулам (1.3) и (1.5) получим:
По этим координатам находим точку С – центр тяести сечения. Она лежит на линии, соединяющей точки С1 и С2, ближе к фигуре, имеющей большую площадь.
Пример 1.2. Вычислить ординату центра тяжести половины круга (рис. 1.2, б).
Решение. Пользуемся формулой
Вычисляем числитель, используя уравнение окружности х2 + y2 = R2:
Вычисляем ус
Полезные ссылки
1. Пример расчета геометрических характеристик
2. Расчет характеристик он-лайн (программа)
::Оглавление::
Сообщество
Вход
Решение задач
Расчет редукторов
Для Android (рекомендую)
NEW Mobile Beam 2.0
Программа для расчета балок на прочность на Вашем Android устройстве…
Java 2 ME
Источник
Известны
три геометрические характеристики –
это длина, площадь, объем, которые имеют
определенный физический смысл. Рассмотрим
новые характеристики, которые будут
использоваться в расчетных формулах
сопротивления материалов: статические
моменты и моменты инерции площадей
сечений. Эти характеристики не имеют
прямого физического смысла. Их нельзя
измерить привычным путем. При выводе
формул сопротивления материалов иногда
случается, что их часть представляет
собой интегральное выражение, зависящее
только от формы и размеров сечения. Для
упрощения последующего использования
этих формул удобно такое выражение
подсчитать заранее для различных форм
сечений.
Статические
моменты площади сечений используются
при определении положения центра тяжести
сечения, при расчете касательных
напряжений при изгибе.
Моменты
инерции используются при расчете
напряжений и перемещений при изгибе,
кручении и т. д.
3.1. Статические моменты площади сечений
Статическими
моментами площади сечения называются
интегралы следующего вида:
![]() ,
,
![]()
В
целях их геометрической интерпретации
рассмотрим сечение произвольной формы
(рис. 3). Выделим в сечении элементарную
площадку dA
с координатами
y
и z.
Произведение
площади dA
на координату
y
есть элементарный
статический момент dSz
относительно
оси z.
Это понятие
аналогично моменту силы относительно
оси. Если предположить, что А
– это вес
пластины, имеющей форму нашего сечения,
то статический момент Sz
– это момент
силы тяжести пластины относительно оси
z.
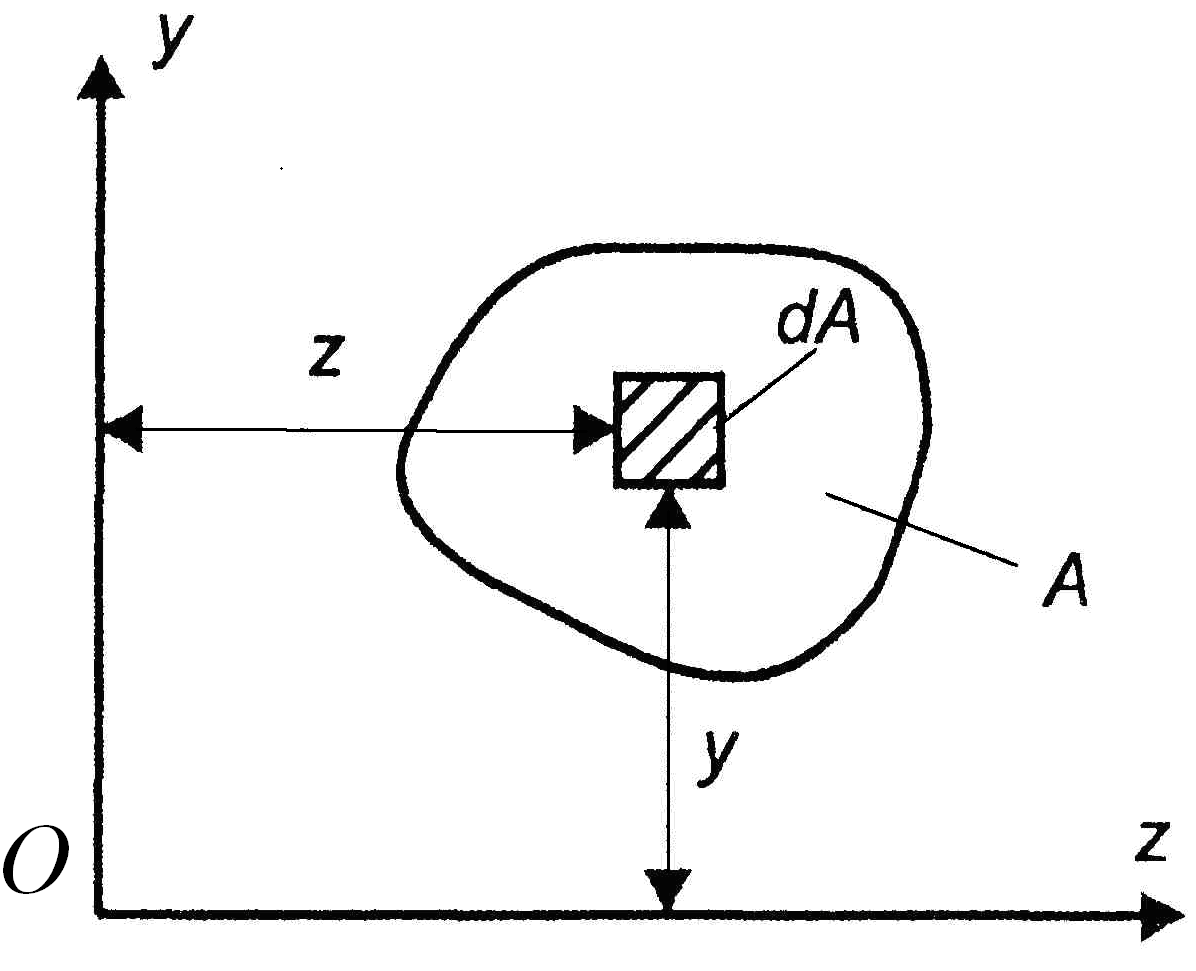
Рис.
3. Сечение произвольной формы в системе
координат z
О y
3.1.1. Свойства статических моментов площади сечения
Размерность статических моментов –
[длина3], обычно [м3] или
[см3].
Статические моменты могут быть
положительными, отрицательными или
равными нулю.
Ось, относительно которой статический
момент равен нулю, называется центральной.
Точка пересечения центральных осей
называется центром тяжести сечения.
Статический момент составного сечения
равен сумме статических моментов
элементов этого сечения. Это вытекает
из свойств определенного интеграла,
который можно вычислять по частям (в
нашем случае по частям площади А).
3.1.2. Определение положения центра тяжести
Рассмотрим
изменение статического момента при
параллельном переносе осей координат
(рис. 4). Расстояние между осями координат
обозначим а
и b.
Пусть известны статические моменты
относительно осей координат z,
y.
Найдем
статические моменты относительно
параллельных осей координат z1,
y1.

Рис.
4. Сечение произвольной формы в системах
координат с
параллельными
осями
По
определению: ![]() ,
,![]() .
.
Выделим
элементарную площадку dA
и запишем
связь между координатами площадки в
старой и новой системах координат: z1
= z
– b,
y1
= y
– a.
Тогда .
Аналогично
.
Найдем,
насколько надо сместить оси, чтобы они
стали центральными.
,
,
,
.
Здесь
ус
и zc
– координаты
центра тяжести.
При
их определении сечение разбиваем на
такие элементы, для которых эти координаты
известны (прямоугольник, круг, треугольник
и др.).
На
рис. 5 сечение разбито на три прямоугольника.
Статический момент каждого элемента
найдем формулам: Szi
= усi∙
Аi
и Syi
= zci
∙ Аi.

Рис.
5. Разбиение сложного сечения на простые
элементы
Суммарный
статический момент всего сечения, как
сказано выше, равен сумме статических
моментов элементов этого сечения:
Sz
= Sz1
+ Sz2
+ Sz3
= A1
∙ y1
+ A2
∙ y2
+ A3
∙ y3;
Sy
= Sy1
+ Sy2
+ Sy3
= A1
∙ z1
+ A2
∙ z2
+ A3
∙ z3,
а
площадь – сумме площадей элементов А
= A1
+ A2
+ A3.
Таким
образом, координаты центра тяжести
сечения можно представить в виде:
 ;
;
 .
.
где
Ai,
yi,
zi
– площади и координаты центра тяжести
элементов, на которые разбито сечение,
n
– количество
элементов.
Источник
Макеты страниц
Статическим моментом сечения относительно некоторой оси называется взятая по всей его площади F сумма произведений элементарных площадок на их расстояния от этой оси, т. е.
Статические моменты выражаются в и т. д.
Для сложного сечения, состоящего из частей, выражения (2.5) можно представить в виде
где — статические моменты части сечения относительно осей и у соответственно.
Итак, статический момент сложного сечения относительно некоторой оси равен сумме статических моментов всех частей этого сечения относительно той же оси.
Нельзя суммировать статические моменты частей сечения, вычисленные относительно различных осей.
Рис. 2.5
Рис. 3.5
Рассмотрим сечение, показанное на рис. 2.5. Очевидно, что статический момент части сечения, расположенной выше оси 2, положителен, так как для любой площадки этой части ординаты у положительны; для части же сечения, расположенной оси , статический момент отрицателен и меньше по абсолютной величине. Поэтому статический момент всего рассматриваемого сечения положителен.
Если за положительное для оси у выбрать направление вниз (а не вверх, как на рис. 2.5), то интеграл станет отрицательным, а интеграл — положительным; статический момент всего сечения, равный сумме этих интегралов, станет отрицательным.
Таким образом, изменение положительного направления оси у вызывает изменение знака статического момента аналогично изменение положительного направления оси вызывает изменение знака статического момента
Рис. 4.5
Рис. 5.5
Установим зависимость между статическими моментами одного и того же сечения относительно двух параллельных друг другу осей (рис. 3.5). Выражения статических моментов относи тельно этих осей на основании (2.5) имеют вид
но
и, следовательно,
Окончательно
и аналогично
Найдем теперь положение осей , и (рис. 4.5), относительно которых статические моменты равны нулю. Для этого приравняем нулю выражения (4.5) и (5.5):
откуда
Точка пересечения таких осей (точка С на рис. 4.5) называется центром тяжести сечения, а оси, проходящие через центр тяжести, — центральными осями. Относительно любой оси, проходящей через центр тяжести сечения (т. е. относительно любой центральной оси), статический момент равен нулю.
Формулы (6.5) используются для определения координат центра тяжести сечения.
Для случаев, когда положение центра тяжести сечения известно, а требуется определить статические моменты сечения относительно любых осей у и z (рис. 5.5), формулы (6.5) преобразуются к виду
Определим для примера положение центра тяжести сечения, показанного на рис. 6.5. Для этого разобьем сечение на две части: прямоугольник площадью и квадрат площадью Центры тяжести этих частей показаны на рис. 6.5.
Рис. 6.5
Проведем случайные оси у и . Вычислим статический момент сечения относительно оси :
В этом выражении — статические моменты частей сечения площадями относительно оси , равные [на основании выражения (7.5)]:
Следовательно,
и на основании выражения (6.5)
где
Аналогично
где
Следовательно,
По найденным значениям координат на рис. 6.5 установлено положение центра тяжести С заданного сечения.
Положение центра тяжести того же сечения (см. рис. 6.5) можно найти более просто, если случайные оси провести через центр тяжести одной из частей, на которые разбито сечение.
Рис. 7.5
Рис. 8.5
Будем, например, рассматривать площадь заданного сечения как разность площадей квадрата квадрата 2, 5, 6, 7, так как заданное сечение можно получить путем вычитания квадрата из квадрата (рис. 7.5). Тогда относительно осей у и z, показанных на рис. 7.5:
(здесь так как ось 2 проходит через центр тяжести квадрата
Найденное положение центра тяжести С заданного сечения показано на рис. 7,5; оно совпадает с полученным выше (см. рис. 6.5).
Заметим, что разбивку сечения на составные части несколькими способами или выбор различных координатных систем (или то и другое) надо широко использовать для контроля правильности определения положения центра тяжести.
Следует иметь в виду, что при вычислении статических моментов сечений необходимо учитывать знаки координат центров тяжести отдельных частей фигуры. Так, например, при вычислении статического момента сечения (рис. 8.5) относительно оси абсциссу следует взять со знаком «минус»:
На основании рассмотренных примеров можно установить следующий порядок определения положения центра тяжести сложного сечения.
1. Сложное сечение разбивается на части, имеющие вид простых фигур.
2. Определяются площади и положения центров тяжести каждой фигуры.
3. Выбираются случайные координатные оси у и 2.
4. По формулам (7.5) вычисляются статические моменты каждой фигуры относительно осей у и . Затем путем суммирования значений [в соответствии с выражениями (3.5)] определяется статический момент а значений – статический момент всего сечения.
5. По формулам (6.5) вычисляются координаты центра тяжести всего сечения.
В отдельных случаях, когда заданное сечение нельзя разбить на такие фигуры, положения центров тяжести которых известны, положение центра тяжести всего сечения необходимо определять путем непосредственного интегрирования. Такие случаи рассмотрены в примере 1.5.
Источник
Сопротивление материалов
При некоторых видах деформаций прочность и жесткость (способность противостоять деформации) элементов конструкций зависит не только от величины поперечного сечения, но и от формы этого сечения. 
Самый простой пример – обыкновенную школьную линейку можно легко изогнуть относительно широкой стороны поперечного сечения и совершенно невозможно изогнуть относительно его короткой стороны. При этом общая площадь сечения в обоих случаях одинакова. На основании этого примера становится очевидным, что на сопротивление некоторым видам деформации оказывает влияние (иногда – решающее) не только величина площади сечения бруса, но и его геометрическая форма.
При изучении деформаций изгиба и кручения нам потребуется знание некоторых геометрических характеристик плоских сечений, которые оказывают влияние на способность конструкций сопротивляться деформациям относительно той или иной оси либо полюса (точки).
Чтобы понять суть явления и влияния этих геометрических характеристик на сопротивление бруса, например, изгибу, следует обратиться к основополагающим постулатам сопромата. Как известно из установленного в 1660 году английским физиком Робертом Гуком закона, напряжение в сечениях бруса прямо пропорционально его относительному удлинению. Очевидно, что волокна, расположенные дальше от оси изгиба, растягиваются (или сжимаются) сильнее, чем расположенные вблизи оси. Следовательно, и напряжения возникающие в них будут бόльшими.
Можно привести условную сравнительную аналогию между напряжением в разных точках сечения бруса с моментом силы – чем больше плечо силы – тем больше ее момент (относительно оси или точки). Аналогично – чем дальше от какого-либо полюса (оси) отстоит точка в сечении, тем большее напряжение в ней возникает при попытке изогнуть или скрутить брус относительно этого полюса (оси).
***
Статический момент площади
Статическим моментом площади плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений элементарных площадок (Si) на расстояния (ri)от них до этой оси.

Если упростить это определение, то статический момент инерции плоской фигуры относительно какой-либо оси (лежащей в той же плоскости, что и фигура) можно получить следующим образом:
- разбить фигуру на крохотные (элементарные) площадки (рис. 1);
- умножить площадь каждой площадки на расстояние ri от ее центра до рассматриваемой оси;
- сложить полученные результаты.
Статический момент площади плоской фигуры обозначают S с индексом оси, относительно которой он рассматривается: Sx, Sy, Sz.
Примечание: в разных учебниках или других источниках информации обозначение тех или иных физических величин может отличаться от приведенных на этом сайте. Как вы понимаете, от условного обозначения величин суть описываемых явлений и закономерностей не изменяется.
Sx = Σ y dA; Sy = Σ x dA.
Анализ этих формул позволяет сделать вывод, что статический момент площади фигуры относительно оси, лежащей в этой же плоскости, равен произведению площади фигуры на расстояние от ее центра тяжести до этой оси.
Из этого вывода следует еще один вывод – если рассматриваемая ось проходит через центр тяжести плоской фигуры, то статический момент этой фигуры относительно данной оси равен нулю.
Единица измерения статического момента площади – метр кубический (м3).
При определении статического момента площади сложной фигуры можно применять метод разбиения, т. е. определять статический момент всей фигуры, как алгебраическую сумму статических моментов отдельных ее частей. При этом сложная геометрическая фигура разбивается на простые по форме составные части – прямоугольники, треугольники, окружности, дуги и т. п., затем для каждой из этих простых фигур подсчитывается статический момент площади, и определяется алгебраическая сумма этих моментов.
***
Полярный момент инерции
Полярным моментом инерции плоской фигуры относительно полюса (точки), лежащего в той же плоскости, называется сумма произведений элементарных площадок (Si) этой фигуры на квадрат их расстояний (r2i) до полюса.
Полярный момент инерции обозначают Iρ (иногда его обозначают Jρ), а формула для его определения записывается так:
Iρ = Σ ρ2 dA.
Единица измерений полярного момента инерции – м4, из чего следует, что он не может быть отрицательным.
Понятие полярного момента инерции понадобится при изучении деформаций кручения круглых валов, поэтому приведем формулы для определения полярного момента квадратного, круглого и кольцевого сечения.
Очевидно, что полярный момент инерции кольцевого сечения равен разности полярных моментов инерции большого и малого кругов, ограничивающих это сечение.
***
Осевой момент инерции
Осевым моментом инерции плоской фигуры относительно оси, лежащей в той же плоскости, называется взятая по всей площади сумма произведений площадей элементарных площадок на квадрат расстояний от них до этой оси (рис).

Осевой момент инерции обозначается I (иногда – J)с индексом, соответствующим оси:
Ix = Σ y2 dA; Iy = Σ x2 dA.
Если при этом площадь элементарных площадок принять стремящимися к минимуму, то можно использовать методы интегрального исчисления, заменив знак суммы Σ на знак интеграла ∫.
Очевидно, что осевой и полярный момент инерции выражаются в одинаковых единицах – м4. Осевой момент инерции величина всегда положительная и не равна нулю (м4 не может быть отрицательным, а площадь не может быть равной нулю, иначе пропадает и сама фигура, как площадка).
Если сложить осевые моменты инерции плоской фигуры относительно перпендикулярных осей, то получим полярный момент инерции этой фигуры относительно точки пересечения этих осей (начала координат), т. е. :
Ix + Iy = Iρ.
Так как интеграл суммы равен сумме интегралов, то момент инерции сложной фигуры можно вычислить как сумму моментов инерции простых фигур, на которые разбивают сложную фигуру.
Понятие осевого момента инерции понадобится при изучении теории изгиба.
Приведем формулы для определения осевых моментов инерции наиболее часто встречающихся при расчетах форм сечений:
Для прямоугольника размером b × h: | Ix = bh3 /12 | ||
Для квадрата со стороной а: | Ix = a4 / 12 | ||
Для круга диаметром d: | Ix = Iy≈ 0,05 d4 | ||
Для кольцевого сечения размером D × d: | Ix = Iy≈ 0,05 (D4 – d4) |

***
Момент инерции при параллельном переносе осей
Оси, проходящие через центр тяжести плоской фигуры, называют центральными осями.
Момент инерции относительно центральной оси называется центральным моментом инерции.
Теорема
Момент инерции относительно какой-либо оси равен сумме момента инерции относительно центральной оси, параллельной данной, и произведения площади фигуры на квадрат расстояния между осями.

Для доказательства этой теоремы рассмотрим произвольную плоскую фигуру, площадь которой равна А, центр тяжести расположен в точке С, а центральный момент инерции относительно оси x будет Ix.
Вычислим момент инерции фигуры относительно некоторой оси x1, параллельной центральной оси и отстоящей от нее на расстоянии а (рис. 2).
Ix1 = Σ y12 dA + Σ (y + a)2 dA =
= Σ y2 dA + 2a Σ y dA + a2 Σ dA.
Анализируя полученную формулу, отмечаем, что первое слагаемое – осевой момент инерции относительно центральной оси, второе слагаемое – статический момент площади этой фигуры относительно центральной оси (следовательно, он равен нулю), а третье слагаемое после интегрирования может быть представлено в виде произведения a2 A, т. е. в результате получим формулу:
Ix1 = Ix + а2 А – теорема доказана.
На основании теоремы можно сделать вывод, что из ряда параллельных осей осевой момент инерции плоской фигуры будет наименьшим относительно центральной оси.
***
Главные оси и главные моменты инерции
Представим себе плоскую фигуру, моменты инерции которой относительно осей координат Ixи Iy, а полярный момент инерции относительно начала координат равен Iρ. Как было установлено ранее,
Ix + Iy = Iρ.
Если оси координат поворачивать в своей плоскости вокруг начала координат, то полярный момент инерции останется неизменным, а осевые моменты будут изменяться, при этом их сумма останется величиной постоянной. Поскольку сумма переменных величин постоянна, то одна из них уменьшается, а другая увеличивается, и наоборот.
Следовательно, при определенном положении осей один из осевых моментов достигнет максимального значения, а другой – минимального.
Оси, относительно которых моменты инерции имеют минимальное и максимальное значения, называют главными осями инерции.
Момент инерции относительно главной оси называется главным моментом инерции.
Если главная ось проходит через центр тяжести фигуры, она называется главной центральной осью, а момент инерции относительно такой оси – главным центральным моментом инерции.
Можно сделать вывод, что если фигура симметрична относительно какой-нибудь оси, то эта ось всегда будет одной из главных центральных осей инерции этой фигуры.
***
Центробежный момент инерции
Центробежным моментом инерции плоской фигуры называют взятую по всей площади сумму произведений элементарных площадок на расстояние до двух взаимно перпендикулярных осей:
Ixy = Σ xy dA,
где x, y – расстояния от площадки dA до осей x и y.
Центробежный момент инерции может быть положительным, отрицательным и равным нулю.
Центробежный момент инерции входит в формулы для определения положения главных осей несимметричных сечений.
В таблицах стандартных профилей содержится характеристика, которая называется радиусом инерции сечения, вычисляемая по формулам:
ix = √ (Ix / A), iy = √ (Iy / A), (здесь и далее знак “√” – знак корня)
где Ix, Iy – осевые моменты инерции сечения относительно центральных осей; А – площадь сечения.
Эта геометрическая характеристика используется при изучении внецентрального растяжения или сжатия, а также продольного изгиба.
***
Материалы раздела “Сопротивление материалов”:
- Основные понятия и определения
- Растяжение и сжатие
- Смятие. Контактные напряжения
- Деформация сдвига (среза)
- Деформация кручения
- Деформация изгиба
Растяжение и сжатие
Правильные ответы на вопросы Теста № 2
№ вопроса | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
Правильный вариант ответа | 2 | 3 | 2 | 1 | 1 | 3 | 3 | 2 | 2 | 2 |
Источник
