Какими свойствами обладает средняя линия трапеции

Серединный отрезок
Трапеция — фигура (четырехугольник), что состоит из четырех сторон, две из которых лежат на параллельных прямых, а остальные нет. Параллельные — верхнее и нижнее основание, 2 другие имеют название боковых сторон. Из этого следует, что четырехугольник состоит из двух оснований.
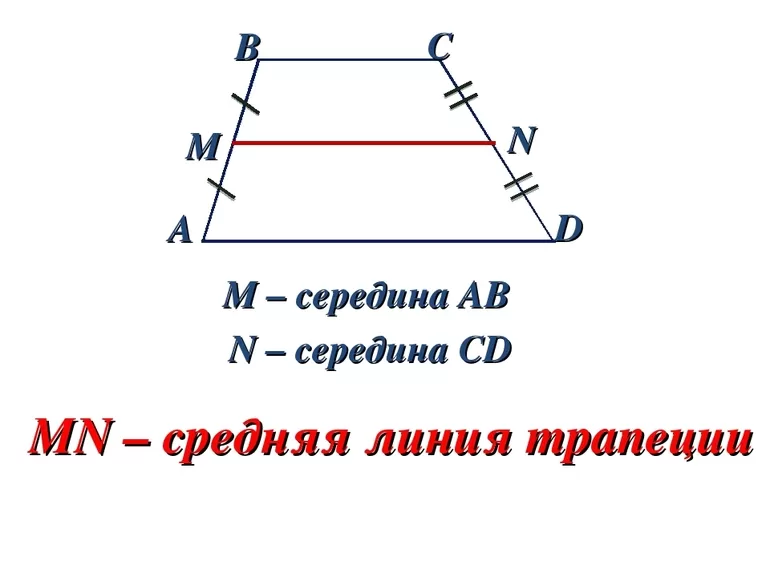
Средняя линия — отрезок, который соединяет середины боков фигуры и обозначается буквой m. Интересно, что если в треугольнике таких отрезков можно провести 3, то в таком четырёхугольнике исключительно одну.
Свойство и формулы
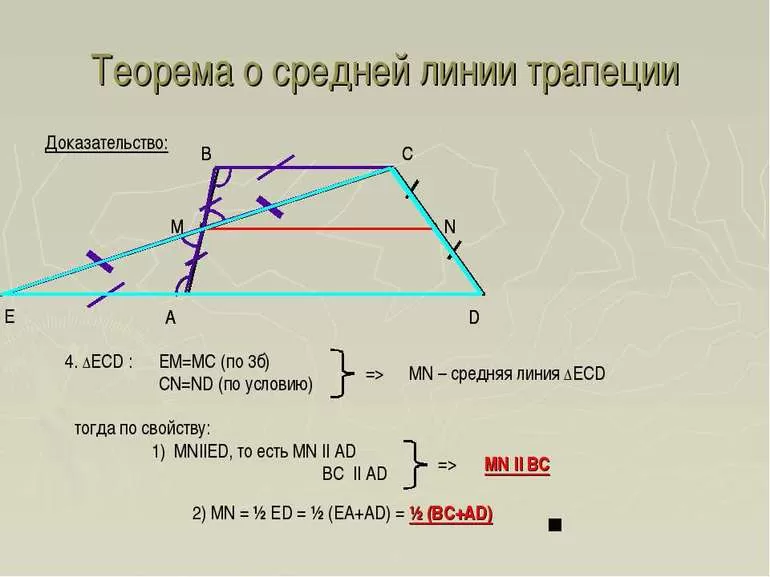
Серединная линия равняется половине сумм длины двух оснований. Это определение является теоремой, доказательство и для того чтобы его сформулировать, необходимо обратить внимание на свойство срединного отрезка в треугольнике.
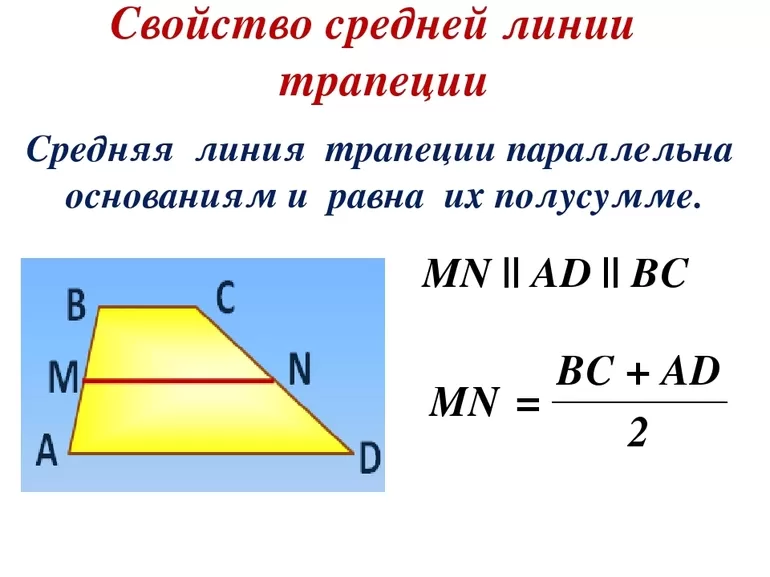
Доказать теорему просто. Для этого в трапеции проводят серединный отрезок так, чтобы он опускался с верхней точки фигуры и пересекался с продленным нижним основанием. Такая линия делит четырёхугольник на два треугольника. Причем средняя линия фигуры также принадлежит треугольнику и выполняет те же функции. Она равна половине нижней стороны, которая состоит из двух отрезков, равных основаниям трапеции.
Свойство такого отрезка — в четырехугольнике он параллелен основаниям. Учитывая эти данные, их можно использовать как признак при решениях различных заданий для выявления этого понятия.
Формула для нахождения записывается так:
m = (a + b) / 2, где a, b — обозначение длины оснований.
Тригонометрия углов применима в формуле:
- m = a — h (ctga +ctg b)/ 2;
- m = b — h (ctga +ctg b)/ 2.
Полусумма оснований трапеции вычисляется через диагонали и их угол пересечения и высоту. Итак, для этого находится:
- m = d 1 d 2 /2 h * sina;
- m = d 1 d 2 /2 h * sinb.
Углы а, b находятся при нижнем основании, а линия h является высотой, проведенной к этому отрезку.
Формула средней линии трапеции через площадь и высоту записывается так:
m = S / h.
Кроме этого, такой отрезок делит фигуру на две части и имеет место соотношение их площадей, которое выражается в виде:
S 1 /S 2 =3a+b/a+3b, где основания a<b.
Все эти формулы используются для решения задач и доказывания определённых утверждений.
Примеры заданий
Серединный отрезок трапеции равен 15 дм, а одно из оснований на 6 дм длиннее от другого. Определить длину параллельных сторон в трапеции.
Чтобы найти нужные стороны, нужно припустить, что на одну приходится х дм, соответственно на другую — (х+6) дм. Учитывая свойство серединного отрезка в этой фигуре, следует, что m = a + b /2.
m =2х+6/2=15, от сюда следует, что х=12 дм.
В результате a =12 дм, b =18 дм.
Следующее задание, где требуется искать стороны, что лежат на параллельных прямых. При этом дано их соотношения 4:7 средняя линия равна 55 дм.
Итак, пусть k — коэффициент пропорциональности, основания относятся как 4 k :7 k. Получается уравнение (4k +7k)/2=55. Отсюда следует, что k =10, то есть на нужные отрезки приходится по 40 и 70 дм.
Таким образом, средняя линия треугольника и трапеции имеет одинаковое свойство. Темы между собой очень похожи. Следовательно, средняя линия трапеции равна половине сумм двух оснований.
Источник
Привет!
Перед тобой лучший гид по трапеции! Только то, что нужно. Без воды.
Основные определения, формулы и свойства.
Помни о своей цели!
Тебе нужно подготовиться к ЕГЭ по математике так, чтобы поступить в ВУЗ мечты! Будь уверен!
Приступим!
НАЧАЛЬНЫЙ УРОВЕНЬ
Что такое трапеция?
![]()
Трапеция – такой четырехугольник, у которого две стороны параллельны, а две другие – нет.
Параллельные стороны называются – основания, а непараллельные стороны называются боковые стороны.
Вот, смотри:
![]()
Оказывается, трапеция (как и треугольник) бывает равнобедренная.
![]()
Если боковые стороны трапеции равны, то она называется равнобедренной (или равнобокой).
И тут возникает вопрос: а могут ли у трапеции быть равными ОСНОВАНИЯ?
А вот и нет. Тогда это получится не трапеция, а параллелограмм, потому что две стороны окажутся параллельны и равны (вспоминаем признаки параллелограмма)
Свойства трапеции
Итак, что ты должен знать о свойствах трапеции…
![]()
Сумма углов при каждой боковой стороне трапеции равна 180°.
(у нас на рисунке ( displaystyle angle 1+angle 2=180{}^circ ) и ( displaystyle angle 3+angle 4=180{}^circ ))
Почему так? Ну, конечно, просто потому, что основания – параллельны, а боковая сторона – секущая. Вот и получается, что ( displaystyle angle 1) и ( displaystyle angle 2) – внутренние односторонние углы при параллельных ( displaystyle AD) и ( displaystyle BC) и секущей ( displaystyle AB). Поэтому ( displaystyle angle 1+angle 2=180{}^circ ). И точно так же ( displaystyle angle 3) и ( displaystyle angle 4) – внутренние односторонние углы при тех же параллельных ( displaystyle AD) и ( displaystyle BC), но секущая теперь – ( displaystyle CD).
Видишь: главное, что играет роль – это параллельность оснований. Давай разберем еще некоторые свойства трапеции.
Как у всякого четырехугольника, у трапеции есть диагонали. Их две – посмотри на рисунки:
![]()
![]()
Снова порассуждаем об углах:
![]()
Опять ( displaystyle AD) и ( displaystyle BC) – параллельные, а диагональ ( displaystyle AC) – секущая. Поэтому ( displaystyle angle 1=angle 2).
А теперь рассмотрим сразу 2 диагонали и 4 угла:
![]()
( displaystyle angle 1=angle 2)
( displaystyle angle 3=angle 4)
Что из этого может следовать?
Очень важный факт:
Треугольники ( displaystyle BOC) и ( displaystyle AOD) – подобны по двум углам.
Их коэффициент подобия равен отношению оснований: ( displaystyle K=frac{a}{b}).
Средняя линия трапеции
Для начала – что же такое средняя линия трапеции?
![]()
Средняя линия трапеции – это отрезок, который соединяет середины боковых сторон трапеции.
Оказывается, длину этой средней линии можно выразить через длины оснований трапеции. А именно, имеет место такая формула:
![]()
( displaystyle m=frac{a+b}{2}), то есть:
Длина средней линии трапеции равна полусумме (то есть половине суммы) длин оснований.
А ещё:
Средняя линия трапеции параллельна ее основаниям.
Трапеция, вписанная в окружность
Даже если ты ещё не изучал темы «Окружность. Вписанный угол» и «Вписанный четырехугольник», тебе будет полезно (и, надеюсь, интересно) узнать следующий удивительный факт:
Это закрытый контент
Оставьте E-mail и получите доступ к нему
![]()
Если трапецию можно вписать в окружность, то она – равнобокая.
Доказывать это мы не будем (здесь, во всяком случае), а вот запомнить хорошо бы – пригодится!
Подведём итог – он короткий.
Самое важное, что есть в трапеции – две параллельные стороны и BCE свойства трапеции именно этим и определяются.
Так что, если у тебя в задаче трапеция, – используй параллельность и всё получится!
![]()
Трапеция – такой четырехугольник, у которого две стороны параллельны, а две другие – нет.
![]()
Параллельные стороны называются основаниями, а непараллельные – боковыми сторонами.
![]()
Если боковые стороны трапеции равны, то она называется равнобедренной (или равнобокой).
![]()
Сумма углов при каждой боковой стороне трапеции равна 180°.
(у нас на рисунке ( displaystyle angle 1+angle 2=180{}^circ ) и ( displaystyle angle 3+angle 4=180{}^circ ))
Почему? ( displaystyle AD) и ( displaystyle BC) – параллельны, а ( displaystyle AB) и ( displaystyle CD) – секущие, поэтому:
- ( angle 1+angle 2=180{}^circ );
- ( angle 3+angle 4=180{}^circ ).
![]()
Треугольники ( displaystyle BOC) и ( displaystyle AOD) подобны по двум углам.
(( displaystyle angle 1=angle 2) и ( displaystyle angle 3=angle 4) – как накрест лежащие)
Коэффициент подобия треугольников ( displaystyle BOC) и ( displaystyle AOD) равен отношению оснований:
( K=frac{a}{b})
Сначала сформулируем основное определение, которое тебе нужно знать для понимания этого свойства трапеции:
![]()
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
А теперь формула:
А вот и само третье свойство трапеции:
Средняя линия трапеции равна полусумме оснований и параллельна им.
А это почему? Ту чуть – чуть сложнее – потребуется провести аж одну лишнюю линию!
![]()
Итак, проведём ( displaystyle CEparallel AB). Тогда четырехугольник ( displaystyle ABCE) – параллелограмм.
Возьмём середину ( displaystyle M) стороны ( displaystyle AB) и середину ( displaystyle K) стороны ( displaystyle CE).
Оба: ( displaystyle MBCK) и ( displaystyle AMKE) – снова параллелограммы (( displaystyle MBparallel CK) и ( displaystyle MB=CK); ( displaystyle AMparallel KE) и ( displaystyle AM=KE)).
Ну вот, значит ( displaystyle MKparallel AD), да ещё ( displaystyle MK=BC=a).
Поедем дальше.
![]()
Проведём ( displaystyle KN) – среднюю линию в ( displaystyle Delta ECD).
Знаем, что ( displaystyle KNparallel ED) и ( KN=frac{1}{2}ED)
Что же из всего этого следует?
![]()
- ( displaystyle MNparallel AD) (так как через точку ( displaystyle K) можно провести лишь одну прямую параллельную ( displaystyle AD), поэтому ( displaystyle MK) и ( displaystyle KN) – одна прямая ( displaystyle MN))
- ( displaystyle MN=MK+KN=a+frac{b-a}{2})
( displaystyle MN=frac{a+b}{2})
Вот и доказали!
![]()
Если трапеция вписана в окружность, то она равнобокая.
Почему? Подробнее смотри в теме «Вписанный четырехугольник», а тут – двумя строчками:
( angle 1+angle 2=180{}^circ ) (трапеция же!)
( angle 3+angle 2=180{}^circ ) (вписанный четырехугольник)
( Rightarrow angle 1=angle 3). Ну, и так же ( angle 2=angle 4).
Это закрытый контент
Оставьте E-mail и получите доступ к нему
![]()
В любой трапеции следующие четыре точки лежат на одной прямой:
- ( displaystyle E) – точка пересечения продолжений боковых сторон;
- ( displaystyle F) и ( displaystyle H) – середины оснований;
- ( displaystyle G) – точка пересечения диагоналей.
Эту теорему доказывать не будем – не пугайся.
Заметим только, что ВЕРНО и ОБРАТНОЕ:
Если в каком-нибудь четырехугольнике какие-нибудь три из перечисленных четырёх точек окажутся на одной прямой, то четырёхугольник этот – ТРАПЕЦИЯ.
![]()
Биссектрисы углов при боковой стороне трапеции перпендикулярны.
( left{ begin{array}{l}angle 1+angle 2+angle 3+angle 4=180{}^circ -так, как, трапеция\angle 1=angle 2\angle 3=angle 4 -так, как, биссектрисаend{array} right.Rightarrow 2cdot angle 2+2cdot angle 3=180{}^circ Rightarrow )
( angle 2+angle 3=90{}^circ Rightarrow angle AEB =90{}^circ )
Здесь мы ещё раз увидим, как полезно в трапеции бывает провести линию, параллельную или боковой стороне, или диагонали – сразу появляется новый взгляд. Один раз мы уже так делали – в пункте про среднюю линию. А теперь ты узнал новый факт, который относительно часто встречается в задачах.
В трапеции с перпендикулярными диагоналями ( FH=frac{AD+BC}{2})
Давай докажем! Это уже целая задача, которая вполне может попасться прямо на экзамене!
Это закрытый контент
Оставьте E-mail и получите доступ к нему
Ну вот, и ты теперь старайся с помощью новых знаний и методов решать задачки про трапецию – они обычно не слишком сложные. Главное, твёрдо помнить все свойства трапеции и не забывать о параллельности оснований и иногда (в задачах посложнее) бывает полезно провести что-то параллельное или соединить боковые стороны.
![]()
Проведём ( displaystyle BKparallel AC) и ( displaystyle BLparallel FH).
Обозначим ( displaystyle BC=text{ }a); ( displaystyle AD=b).
Тогда:
- ( displaystyle Delta KBD) – прямоугольный
- ( begin{array}{l}left{ begin{array}{l}LD=frac{b}{2}+frac{a}{2}=frac{a+b}{2}\LK=a+frac{b}{2}-frac{a}{2}=frac{a+b}{2}end{array} right.Rightarrow BL-медиана~в~ Delta KBD.\end{array})
Значит, ( BL=frac{KD}{2}) (медиана, проведенная к гипотенузе, равна её половине).
То есть ( BL=frac{a+b}{2}).
Но ведь ( displaystyle FH=BL) (так как ( displaystyle BFHL) – параллелограмм)( Rightarrow ) ( FH=frac{a+b}{2}).
Трапеция – четырёхугольник, у которого две стороны параллельны (они называются основания), а две другие – нет (это боковые стороны).
![]()
- Сумма углов при каждой боковой стороне трапеции равна 180°
- ( displaystyle angle 1+angle 2=180{}^circ ) и ( displaystyle angle 3+angle 4=180{}^circ )
![]()
Средняя линия трапеции (( displaystyle MN)) – отрезок, соединяющий середины боковых сторон:
( displaystyle AM=MB, CN=ND).
- Средняя линия параллельна основаниям: ( displaystyle MNparallel BCparallel AD).
- Длина средней линии трапеции равна полусумме длин оснований: ( displaystyle MN=frac{BC+AD}{2}).
![]()
- Диагонали любой трапеции пересекаются в точке О.
- Треугольники, образованные основаниями трапеции и отрезками диагоналей
(( displaystyle BOC) и ( displaystyle AOD)) подобны по двум углам с коэффициентом подобия равным отношению оснований: ( displaystyle k=frac{BC}{AD}). - Площади треугольников, образованных боковыми сторонами и отрезками диагоналей трапеции, равны: ( displaystyle {{S}_{Delta AOB}}={{S}_{Delta COD}}).
![]()
Равнобедренная (равнобокая) трапеция – это трапеция, у которой боковые стороны равны:
( displaystyle AB=CD).
Свойства равнобедренной трапеции:
- диагонали равны: ( displaystyle AC=BD);
- углы при основании равны: ( displaystyle angle A=angle D,text{ }angle B=angle C);
- сумма противолежащих углов равна ( displaystyle 180{}^circ ): ( displaystyle angle A+angle C=angle B+angle D=180{}^circ ).
![]()
- Если трапецию можно вписать в окружность, то она – равнобокая.
- Стороны и диагональ равнобокой трапеции связаны соотношением: ( displaystyle A{{C}^{2}}=B{{D}^{2}}=ADcdot BC+A{{B}^{2}}).
Площадь трапеции равна полусумме оснований, умноженной на высоту: ( displaystyle {{S}_{ABCD}}=frac{BC+AD}{2}cdot h).
P.S. Последний бесценный совет ????
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
- проверить свою готовность к каждому типу задач на ЕГЭ (пройдя тест);
- подтянуть слабые места с помощью видеоуроков, вебинаров;
- понять тему с помощью статей учебника YouClever;
- набить руку, решая задачи и получая проверку и решения;
- сдать пробный ЕГЭ и получить сразу оценку и разбор ошибок.
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Скажи погромче!
Если умеешь решать задачи по свойствам трапеции об окружности и о сумме сторон, поздравляю, ты сделал шаг в олимпиадный уровень!
А еще задачи по этой теме встречаются особенно часто во второй части ОГЭ.
Понравилась ли тебе статья? Все ли было понятно?
Если есть вопросы или предложения, пиши нам внизу в комментариях! А еще пиши, что думаешь о статье в целом ????
Мы читаем все и будем очень рады узнать.
Удачи!
Источник
[{Large{text{Произвольная трапеция}}}]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна (180^circ).
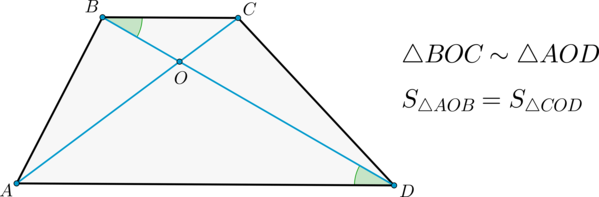
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
Доказательство
1) Т.к. (ADparallel BC), то углы (angle BAD) и (angle ABC) – односторонние при этих прямых и секущей (AB), следовательно, (angle
BAD
+angle ABC=180^circ).
2) Т.к. (ADparallel BC) и (BD) – секущая, то (angle DBC=angle
BDA) как накрест лежащие.
Также (angle BOC=angle AOD) как вертикальные.
Следовательно, по двум углам (triangle BOC sim triangle AOD).
Докажем, что (S_{triangle AOB}=S_{triangle COD}). Пусть (h) – высота трапеции. Тогда (S_{triangle ABD}=frac12cdot hcdot
AD=S_{triangle ACD}). Тогда: [S_{triangle AOB}=S_{triangle ABD}-S_{triangle AOD}=S_{triangle ACD}-S_{triangle AOD}=S_{triangle
COD}]
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
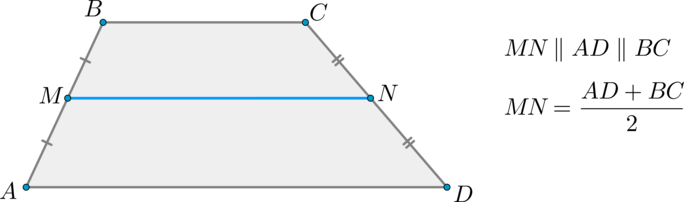
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем параллельность.
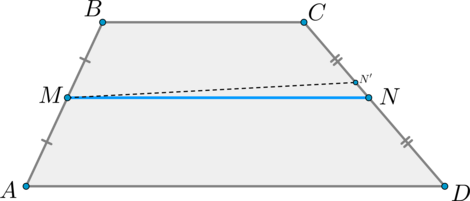
Проведем через точку (M) прямую (MN’parallel AD) ((N’in CD)). Тогда по теореме Фалеса (т.к. (MN’parallel ADparallel BC, AM=MB)) точка (N’) — середина отрезка (CD). Значит, точки (N) и (N’) совпадут.
2) Докажем формулу.
Проведем (BB’perp AD, CC’perp AD). Пусть (BB’cap MN=M’, CC’cap
MN=N’).
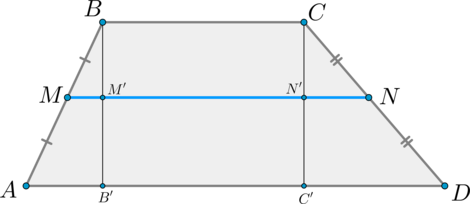
Тогда по теореме Фалеса (M’) и (N’) — середины отрезков (BB’) и (CC’) соответственно. Значит, (MM’) – средняя линия (triangle
ABB’), (NN’) — средняя линия (triangle DCC’). Поэтому: [MM’=dfrac12 AB’, quad NN’=dfrac12 DC’]
Т.к. (MNparallel ADparallel BC) и (BB’, CC’perp AD), то (B’M’N’C’) и (BM’N’C) – прямоугольники. По теореме Фалеса из (MNparallel AD) и (AM=MB) следует, что (B’M’=M’B). Значит, (B’M’N’C’) и (BM’N’C) – равные прямоугольники, следовательно, (M’N’=B’C’=BC).
Таким образом:
[MN=MM’+M’N’+N’N=dfrac12 AB’+B’C’+dfrac12 C’D=] [=dfrac12 left(AB’+B’C’+BC+C’Dright)=dfrac12left(AD+BCright)]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
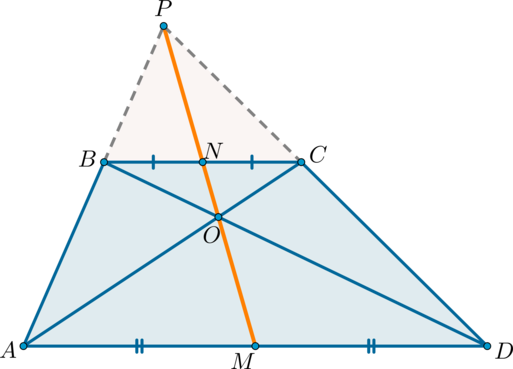
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки (P), (N) и (M) лежат на одной прямой.
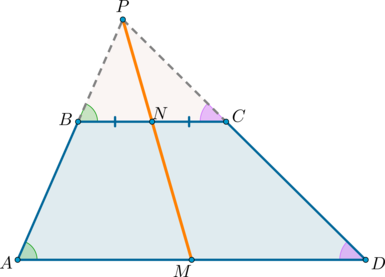
Проведем прямую (PN) ((P) – точка пересечения продолжений боковых сторон, (N) – середина (BC)). Пусть она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
Рассмотрим (triangle BPN) и (triangle APM). Они подобны по двум углам ((angle APM) – общий, (angle PAM=angle PBN) как соответственные при (ADparallel BC) и (AB) секущей). Значит: [dfrac{BN}{AM}=dfrac{PN}{PM}]
Рассмотрим (triangle CPN) и (triangle DPM). Они подобны по двум углам ((angle DPM) – общий, (angle PDM=angle PCN) как соответственные при (ADparallel BC) и (CD) секущей). Значит: [dfrac{CN}{DM}=dfrac{PN}{PM}]
Отсюда (dfrac{BN}{AM}=dfrac{CN}{DM}). Но (BN=NC), следовательно, (AM=DM).
2) Докажем, что точки (N, O, M) лежат на одной прямой.
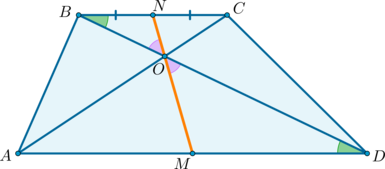
Пусть (N) – середина (BC), (O) – точка пересечения диагоналей. Проведем прямую (NO), она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
(triangle BNOsim triangle DMO) по двум углам ((angle OBN=angle
ODM) как накрест лежащие при (BCparallel AD) и (BD) секущей; (angle BON=angle DOM) как вертикальные). Значит: [dfrac{BN}{MD}=dfrac{ON}{OM}]
Аналогично (triangle CONsim triangle AOM). Значит: [dfrac{CN}{MA}=dfrac{ON}{OM}]
Отсюда (dfrac{BN}{MD}=dfrac{CN}{MA}). Но (BN=CN), следовательно, (AM=MD).
[{Large{text{Равнобедренная трапеция}}}]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию (ABCD).
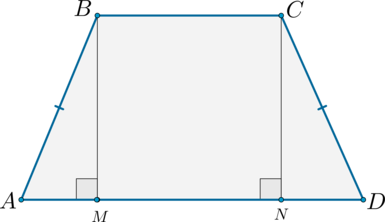
Из вершин (B) и (C) опустим на сторону (AD) перпендикуляры (BM) и (CN) соответственно. Так как (BM
