Какими свойствами обладает сила физика
 Механическое взаимодействие – один из видов взаимодействия материи, способный вызвать изменение механического движения материальных тел.
Механическое взаимодействие – один из видов взаимодействия материи, способный вызвать изменение механического движения материальных тел.
Сила характеризует количественную сторону механического взаимодействия. Таким образом, когда говорят, что на тело действуют силы, то это значит, что на него воздействуют другие тела (или физические поля). Не всегда, впрочем, сила действительно приводит к изменению движению тела; такое изменение может блокироваться действием других сил. С учетом сказанного запишем:
Сила (ньютонова) – мера механического воздействия на некото- рое материальное тело со стороны другого материального тела (или физического поля); она характеризует интенсивность и направление этого воздействия. Это, разумеется, не определение, а лишь пояснение к понятию силы. Поскольку понятие силы – фундаментальное, то его точный смысл раскрывается в аксиомах механики.
Пока же мы отметим вот что. Оговорка “ньютонова” сделана потому, что в динамике мы встретимся с другими величинами, также именуемыми силами, которые, однако, не являются мерами механического взаимодействия. В этом же семестре речь будет идти именно о ньютоновых силах, и мы для краткости будем называть их просто силами.
Далее, под словом “мера” в механике и в физике понимается физическая величина, которая служит для количественного описания какого-либо свойства или отношения. В данном случае речь идет об описании именно механического взаимодействия (а бывают еще, как Вы знаете, и другие взаимодействия – тепло- вые, химические и прочие).
В физике элементарных частиц выделяют четыре фундаментальных взаимодействия: сильное, электромагнитное, слабое и гравитационное. Эти четыре взаимодействия лежат в основе всех наблюдаемых явлений – относящихся как к механике, так и к другим разделам естествознания.
Однако в макромире фундаментальные взаимодействия проявляются, как правило, опосредованно, и нам приходится иметь дело со значительно более широким перечнем взаимодействий (уже не обязательно фундаментальных). Если говорить о механических взаимодействиях, то речь может идти о силах различного происхождения.
Примеры сил: силы тяжести, силы упругости, архимедовы силы, силы сопротивления среды и др. В большинстве задач механики, впрочем, физическая природа тех или иных сил обычно интереса не представляет.
Ещe мы, поясняя понятие силы, говорили об интенсивности и направлении воздействия. Это означает, что сила является векторной величиной. Именно, это – вектор, приложенный к определeнной точке материального тела. Поэтому можно говорить о таких характеристиках силы.
Сила характеризуется:
1) величиной (модулем);
2) направлением;
3) точкой приложения.
К сожалению, на экзамене нередко приходится встречаться с полным пренебрежением к этому правилу. В лучшем случае экзаменатор в этой ситуации поступит так: вздохнет и попросит студента быстренько проставить обозначения векторов в тексте ответа на поставленный вопрос. Если студент не сумеет правильно проставить обозначения – это первый шаг на пути к получению “двойки”. Поэтому, пожалуйста, не игнорируйте в своих конспектах черту, если она написана на доске.
Круглые скобки с запятой в середине обозначают скалярное произведение векторов (запятая при этом разделяет сомножители). Обратите внимание: во многих книгах скалярное произведение обозначается иначе – точкой между век- торами, причем точку обычно можно опустить.
Но мы будем придерживаться именно таких обозначений (они тоже достаточно распространены). Помимо всего прочего, они позволяют избежать путаницы (ведь скалярное произведение векторов нужно отличать от обычного произведения двух скаляров).
Пока мы говорили только о векторе силы. Но понятие силы не сводится к понятию ее вектора. Важна еще и точка приложения силы: ведь если тот же по величине и направлению вектор силы приложить в другой точке тела, то его движение может измениться.
В геометрии принята следующая терминология. Свободный вектор (или просто вектор) – вектор, характеризуемый только модулем и направлением. Связанный вектор – вектор, характеризуемый еще и точкой приложения. Иногда используют такие обозначения.
Через u—.A обозначается связанный вектор, получаемый, если свободный вектор u— приложить в точке A. Обратите внимание: здесь точка пишется не в середине строки (как при умножении чисел), а на ее нижней линии. Таким образом, можно сделать следующий вывод. Итак, сила – связанный вектор (полное обозначение: F—-.A).
Там, где нам потребуется подчеркнуть наличие у силы определенной точки приложения, мы будем пользоваться именно этим полным обозначением. Там, где точка приложения силы будет заранее оговорена, мы будем применять сокращенное обозначение, обозначая силу просто F—- (т.е. так же, как и вектор силы). О точке приложения силы нужно сказать следующее: Если сила действует на материальную точку, то точкой приложения служит сама эта точка.
Если сила действует на материальное тело, то точкой приложения служит точка тела (она может меняться с течением времени). В общем случае точка приложения силы не может лежать вне тела. Если тело – абсолютно твердое, то данное ограничение можно снять; но об этом мы будем говорить позже.
Возникает вопрос: а как можно на практике задать точку приложения силы? Любую точку можно задать, например, ее радиус-вектором, проведенным из некоторого полюса. Полюс – произвольно выделенная точка (положение которой обычно предполагается известным).
Раз здесь говорится “обычно”, то текст в скобках Вы вполне можете игнорировать. Часто бывает так: взяли некоторую точку и объявили ее полюсом (и будет она с этого времени считаться таковым). Но для задания положения точки приложения силы нам как раз нужно знать положение полюса. Можно – но не обязательно – принять за полюс начало системы координат.
Употребляют оба обозначения, но первое предпочтительнее: вектор обозначается одной буквой, а буква “r” напоминает, что речь идет именно о радиус- векторе, или шестью скалярами (Fx , Fy , Fz , xA , yA , zA ). Это – удобно, и так поступают часто. Но задать силу можно также иным способом, который мы рассмотрим в следующем пункте.
Источник
Тестирование онлайн
Что надо знать о силе
Сила – векторная величина. Необходимо знать точку приложения и направление каждой силы. Важно уметь определить какие именно силы действуют на тело и в каком направлении. Сила обозначается как , измеряется в Ньютонах. Для того, чтобы различать силы, их обозначают следующим образом
Ниже представлены основные силы, действующие в природе. Придумывать не существующие силы при решении задач нельзя!
Сил в природе много. Здесь рассмотрены силы, которые рассматриваются в школьном курсе физики при изучении динамики. А также упомянуты другие силы, которые будут рассмотрены в других разделах.
Сила тяжести
На каждое тело, находящееся на планете, действует гравитация Земли. Сила, с которой Земля притягивает каждое тело, определяется по формуле

Точка приложения находится в центре тяжести тела. Сила тяжести всегда направлена вертикально вниз.
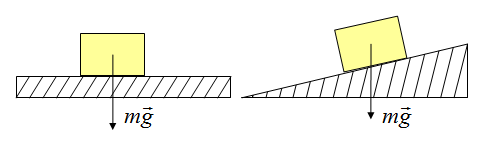
Сила трения
Познакомимся с силой трения. Эта сила возникает при движении тел и соприкосновении двух поверхностей. Возникает сила в результате того, что поверхности, если рассмотреть под микроскопом, не являются гладкими, как кажутся. Определяется сила трения по формуле:

Сила приложена в точке соприкосновения двух поверхностей. Направлена в сторону противоположную движению.
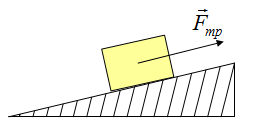
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила реакции опоры
Представим очень тяжелый предмет, лежащий на столе. Стол прогибается под тяжестью предмета. Но согласно третьему закону Ньютона стол воздействует на предмет с точно такой же силой, что и предмет на стол. Сила направлена противоположно силе, с которой предмет давит на стол. То есть вверх. Эта сила называется реакцией опоры. Название силы “говорит” реагирует опора. Эта сила возникает всегда, когда есть воздействие на опору. Природа ее возникновения на молекулярном уровне. Предмет как бы деформировал привычное положение и связи молекул (внутри стола), они, в свою очередь, стремятся вернуться в свое первоначальное состояние, “сопротивляются”.
Абсолютно любое тело, даже очень легкое (например,карандаш, лежащий на столе), на микроуровне деформирует опору. Поэтому возникает реакция опоры.
Специальной формулы для нахождения этой силы нет. Обозначают ее буквой , но эта сила просто отдельный вид силы упругости, поэтому она может быть обозначена и как
Сила приложена в точке соприкосновения предмета с опорой. Направлена перпендикулярно опоре.
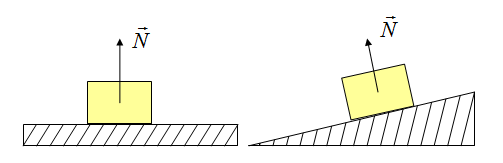
Так как тело представляем в виде материальной точки, силу можно изображать с центра
Сила упругости
Это сила возникает в результате деформации (изменения первоначального состояния вещества). Например, когда растягиваем пружину, мы увеличиваем расстояние между молекулами материала пружины. Когда сжимаем пружину – уменьшаем. Когда перекручиваем или сдвигаем. Во всех этих примерах возникает сила, которая препятствует деформации – сила упругости.
Закон Гука

Сила упругости направлена противоположно деформации.

Так как тело представляем в виде материальной точки, силу можно изображать с центра
При последовательном соединении, например, пружин жесткость рассчитывается по формуле

При параллельном соединении жесткость

Жесткость образца. Модуль Юнга.

Модуль Юнга характеризует упругие свойства вещества. Это постоянная величина, зависящая только от материала, его физического состояния. Характеризует способность материала сопротивляться деформации растяжения или сжатия. Значение модуля Юнга табличное.
Подробнее о свойствах твердых тел здесь.
Вес тела
Вес тела – это сила, с которой предмет воздействует на опору. Вы скажете, так это же сила тяжести! Путаница происходит в следующем: действительно часто вес тела равен силе тяжести, но это силы совершенно разные. Сила тяжести – сила, которая возникает в результате взаимодействия с Землей. Вес – результат взаимодействия с опорой. Сила тяжести приложена в центре тяжести предмета, вес же – сила, которая приложена на опору (не на предмет)!
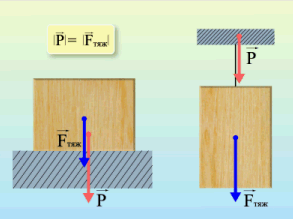
Формулы определения веса нет. Обозначается эта силы буквой .
Сила реакции опоры или сила упругости возникает в ответ на воздействие предмета на подвес или опору, поэтому вес тела всегда численно одинаков силе упругости, но имеет противоположное направление.

Сила реакции опоры и вес – силы одной природы, согласно 3 закону Ньютона они равны и противоположно направлены. Вес – это сила, которая действует на опору, а не на тело. Сила тяжести действует на тело.
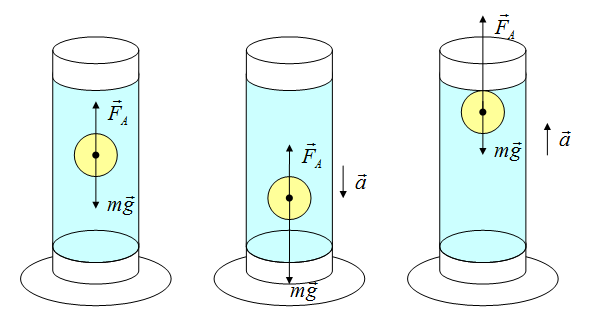
Вес тела может быть не равен силе тяжести. Может быть как больше, так и меньше, а может быть и такое, что вес равен нулю. Это состояние называется невесомостью. Невесомость – состояние, когда предмет не взаимодействует с опорой, например, состояние полета: сила тяжести есть, а вес равен нулю!

Определить направление ускорения возможно, если определить, куда направлена равнодействующая сила
Обратите внимание, вес – сила, измеряется в Ньютонах. Как верно ответить на вопрос: “Сколько ты весишь”? Мы отвечаем 50 кг, называя не вес, а свою массу! В этом примере, наш вес равен силе тяжести, то есть примерно 500Н!
Перегрузка – отношение веса к силе тяжести
Сила Архимеда
Сила возникает в результате взаимодействия тела с жидкость (газом), при его погружении в жидкость (или газ). Эта сила выталкивает тело из воды (газа). Поэтому направлена вертикально вверх (выталкивает). Определяется по формуле:
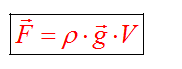
В воздухе силой Архимеда пренебрегаем.
Если сила Архимеда равна силе тяжести, тело плавает. Если сила Архимеда больше, то оно поднимается на поверхность жидкости, если меньше – тонет.
Электрические силы
Существуют силы электрического происхождения. Возникают при наличии электрического заряда. Эти силы, такие как сила Кулона, сила Ампера, сила Лоренца, подробно рассмотрены в разделе Электричество.
Схематичное обозначение действующих на тело сил
Часто тело моделируют материальной точкой. Поэтому на схемах различные точки приложения переносят в одну точку – в центр, а тело изображают схематично кругом или прямоугольником.
Для того, чтобы верно обозначить силы, необходимо перечислить все тела, с которыми исследуемое тело взаимодействует. Определить, что происходит в результате взаимодействия с каждым: трение, деформация, притяжение или может быть отталкивание. Определить вид силы, верно обозначить направление. Внимание! Количество сил будет совпадать с числом тел, с которыми происходит взаимодействие.
Главное запомнить
1) Силы и их природа;
2) Направление сил;
3) Уметь обозначить действующие силы
Силы трения*
Взаимосвязь силы тяжести, закона гравитации и ускорения свободного падения*
Источник
В инерциальной системе отсчета изменение скорости тела возможно только при взаимодействии его с другими телами. Для характеристики этого взаимодействия используют такую физическую величину как сила. Сила дает количественную меру взаимодействия тел.
Виды сил
По своей природе силы могут быть различными. Существуют гравитационные, электрические, магнитные и другие силы. При рассмотрении задач механики физическая природа сил, вызывающих ускорение тела, не является значимой и не рассматривается. При этом для всех видов взаимодействия количественная мера взаимодействия тел выбирается единым образом. Силы разной природы измеряют в одинаковых единицах, при помощи одних и тех же эталонов. В связи с такой универсальностью механика успешно описывает движение под воздействием сил любой природы.
Определение силы в механике отвечает на вопросы: как измерять силу, и какими свойствами она обладает?
Измерение сил
Результатом взаимодействия тел является деформация тела или его ускорение (или то и другое одновременно). Любе проявление силы можно использовать для ее измерения.
Существуют разные способы измерения сил. Например, на основе способности сил вызывать упругую деформацию твердых тел. Самый простой прибор для измерения силы – это пружинный динамометр. Такая модификация динамометра, как крутильные весы, имеют очень высокую чувствительность и являются одним из самых совершенных приборов в физике. При помощи крутильных весов равенство инертной массы и гравитационной было установлено с относительной погрешностью в ${10}^{-12}.$
Для измерения силы на основе явления упругой деформации выбирают, как эталон пружину, для которой известно, что при растяжении на заданную длину пружина действует на закрепленное на ней тело, силой$ F_0$, которая направлена по оси пружины. Считаем, что две любые силы равны и имеют противоположные направления, если они действуют одновременно, а тело в инерциальной системе отсчета находится в покое или равномерно и прямолинейно движется. Тогда такой эталон можно дублировать в любом количестве. Имея описанную выше пружину можно установить наличие силы, но для ее измерения наш динамометр следует градуировать.
Сила – вектор
Сила имеет модуль (величину), направление и точку приложения. Если на тело действуют несколько сил, то их можно заменять равнодействующей силой, которая находится как векторная сумма всех сил, приложенных к телу. И наоборот, любую силу можно разложить на составляющие, векторная сумма которых равна рассматриваемой силе.
Равнодействующую можно найти по правилу треугольника, параллелограмма или многоугольника. Если многоугольник сил будет замкнутым, значит, равнодействующая сила равна нулю.
Часть видов сил зависит от взаимного расположения тел при их взаимодействии, например, гравитационные силы, силы Кулона и т.д. Другие силы зависят от относительной скорости движения тел, находящихся во взаимодействии, например, сила трения. Не смотря на специфику разного рода сил, их общим свойством является то, что они сообщают телам, на которые действуют, ускорения.
Единица измерения силы в Международной системе единиц – ньютон.
[left[Fright]=frac{кгcdot м}{с^2}=Н.]
Основная задача динамики
Основной задачей динамики является изучение и описание движения тел в разных системах отсчета, объяснение причин, определяющих характер их движения. Взаимодействие тел, характеризуемое силами, ведет к изменению характера их движения, следовательно, сила, является важной составляющей большинства законов динамики. Базой классической динамики служат законы Ньютона.
- Первый закон Ньютона: В инерциальной системе отсчета, если на тело не действуют с другие тела или действие их взаимно компенсировано, скорость тела не изменяется ни по модулю, ни по направлению. Тело движется равномерно и прямолинейно.
- Второй закон Ньютона: если тело массы $m$ движется с ускорением $overline{a}$, по отношению к инерциальной системе отсчета, то на него действует сила:
[overline{F}=moverline{a}left(1right).]
Направление ускорения совпадает с направлением, действующей силы.
Закон (1) можно записать в другом виде:
[overline{F}=frac{dleft(moverline{v}right)}{dt}=frac{dleft(overline{p}right)}{dt}left(2right),]
где $overline{p}=moverline{v}$ – импульс тела. Это наиболее общая формулировка основного закона динамики.
Третий закон Ньютона: Если первое тело действует на второе тело с силой ${overline{F}}_{12}$, то в этот же момент тело 2 действует на тело 1 с силой ${overline{F}}_{21}$, при этом:
[{overline{F}}_{12}=-{overline{F}}_{21}left(3right).]
Примеры задач с решением
Пример 1
Задание. На материальную точку действует сила. Под воздействием этой силы точка перемещается по закону $x(t)=A+Bt+t^2-0,1t^3(м)$. В какой момент времени сила равна нулю?
Решение. Основой для решения задачи является второй закон Ньютона:
[overline{F}=moverline{a}left(1.1right).]
Так как уравнение движения тела в условии задачи задано для одной координаты $x$, то будем считать, что движение точки происходит по оси X. Тогда выражение (1.1) можно переписать в виде:
[F=mfrac{d^2x}{dt^2}left(1.2right).]
Вычислим первую, затем вторую производные от $xleft(tright):$
[v_x=frac{dx}{dt}=B+2t-0,3t^2left(1.3right),]
[a_x=frac{d^2x}{dt^2}=2-0,6t left(1.4right).]
Так как масса материальной точки отлична от нуля, для того, чтобы была равна нулю сила должно быть равно нулю ускорение точки. Приравняем полученное ускорение (1.4) к нулю, выразим время:
[a_x=frac{d^2x}{dt^2}=2-0,6t=0to t=3frac{1}{3}left(cright).]
Ответ. $F(t=3frac{1}{3}c)$=0
Пример 2
Задание. Каков коэффициент сопротивления ($mu $) движению материальной точки, массы $m$ в воздухе, если она движется горизонтально, начальная скорость равна $v_0$? Через время $t_1$ эта скорость стала $v_1.$ Силу сопротивления считать пропорциональной квадрату скорости движения точки. Действие силы тяжести не учитывать.
Решение. Запишем выражение силы сопротивления, основываясь на условиях задачи:
[F_s=-mu v^2left(2.1right).]
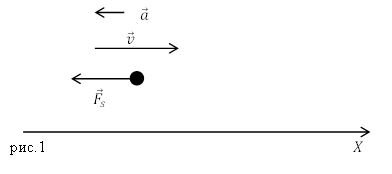
В соответствии с основным законом классической динамики имеем:
[{overline{F}}_s=moverline{a}left(2.1right).]
В проекции на ось X получим:
[F_s=ma=-mu v^2to mfrac{dv}{dt}=-mu v^2left(2.2right).]
мы получили дифференциальное уравнение, которое легко решается методом разделения переменных:
[frac{dv}{v^2}=-frac{mu }{m}dtto -left(frac{1}{v_1}-frac{1}{v_0}right)=-frac{mu }{m}t_1to mu =frac{mleft(v_0-v_1right)}{{t_1v}_1v_0}.]
Ответ. $mu =frac{mleft(v_0-v_1right)}{{t_1v}_1v_0}$
Читать дальше: примеры продольных и поперечных волн.
Источник
