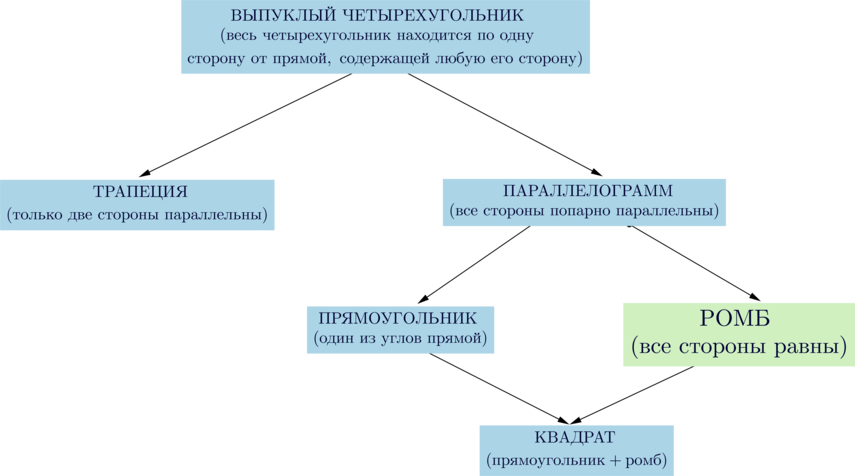
Какими свойствами обладает ромб
У этого термина существуют и другие значения, см. Ромб (значения).
Ромб (др.-греч. ῥόμβος, лат. rombus, в буквальном переводе: «бубен») — это параллелограмм, у которого все стороны равны[1].
Этимология[править | править код]
Термин «ромб» происходит от др.-греч. ῥόμβος — «бубен». Если сейчас бубны в основном делают круглой формы, то раньше их делали как раз в форме квадрата или ромба. Поэтому название карточной масти бубны, знаки которой имеют ромбическую форму, происходит ещё с тех времён, когда бубны не были круглыми.
Слово «ромб» впервые употребляется у Герона и Паппа Александрийского.
Свойства[править | править код]
- Ромб является параллелограммом, поэтому его противолежащие стороны равны и попарно параллельны: АВ || CD, AD || ВС. Противоположные углы ромба равны, а соседние углы дополняют друг друга до 180°.
- Диагонали ромба пересекаются под прямым углом (AC ⊥ BD) и в точке пересечения делятся пополам. Тем самым диагонали делят ромб на четыре прямоугольных треугольника.
- Диагонали ромба являются биссектрисами его углов (∠DCA = ∠BCA, ∠ABD = ∠CBD и т. д.).
- Сумма квадратов диагоналей равна квадрату стороны, умноженному на 4 (следствие из тождества параллелограмма).
- Середины четырех сторон ромба являются вершинами прямоугольника.
- Диагонали ромба являются перпендикулярными осями его симметрии.
- В любой ромб можно вписать окружность, центр которой лежит на пересечении его диагоналей.
Признаки[править | править код]
Параллелограмм является ромбом тогда и только тогда, когда выполняется хотя бы одно из следующих условий[2]:
- Две его смежные стороны равны (отсюда следует, что все стороны равны, ).
- Его диагонали пересекаются под прямым углом (AC ⊥ BD).
- Одна из диагоналей делит содержащие её углы пополам.
Предположим, что заранее не известно, что четырёхугольник является параллелограммом, но дано, что все его стороны равны. Тогда этот четырёхугольник есть ромб[1].
Квадрат, как частный случай ромба[править | править код]
Из определения квадрата, как четырёхугольника, у которого все стороны и углы равны, следует, что квадрат — частный случай ромба. Иногда квадрат определяют, как ромб, у которого все углы равны.
Однако иногда под ромбом может пониматься только четырёхугольник с непрямыми углами, то есть с парой острых и парой тупых углов[3][4].
Уравнение ромба[править | править код]
Уравнение ромба с центром в точке и диагоналями, параллельными осям координат, может быть записано в виде:
где — половины длин диагоналей ромба по осям соответственно.
Длина стороны ромба равна Площадь ромба равна Левый угол ромба рассчитывается по формуле:
Второй угол дополняет его до 180°.
В случае a = b уравнение отображает повёрнутый на 45° квадрат:
где сторона квадрата равна а его диагональ равна Соответственно площадь квадрата равна
Из уравнения видно, что ромб можно рассматривать как суперэллипс степени 1.
Площадь ромба[править | править код]
- Площадь ромба равна половине произведения его диагоналей.
- Поскольку ромб является параллелограммом, его площадь также равна произведению его стороны на высоту.
- Кроме того, площадь ромба может быть вычислена по формуле:
,
где — угол между двумя смежными сторонами ромба.
- Также площадь ромба можно рассчитать по формуле, где присутствует радиус вписанной окружности и угол :
Радиус вписанной окружности[править | править код]
Радиус вписанной окружности r может быть выражен через диагонали p и q в виде:[5]
В геральдике[править | править код]
Ромб является простой геральдической фигурой.
Червлёный ромб в серебряном поле
В червлёном поле 3 сквозных ромба: 2 и 1
Просверленный червлёный ромб в серебряном поле
В лазури левая перевязь, составленная из пяти вертикальных золотых ромбов
Симметрия[править | править код]
Ромб симметричен относительно любой из своих диагоналей, поэтому часто используется в орнаментах и паркетах.
Ромбический орнамент
Ромбические звёзды
Более сложный орнамент
См. другие примеры на Викискладе.
См. также[править | править код]
- Дельтоид
- Звезда (геометрия)
- Ромбододекаэдр
- Ромбоид
Примечания[править | править код]
Литература[править | править код]
- Выгодский М. Я. Справочник по элементарной математике. — М.: Наука, 1978.
- Зайцев В. В., Рыжков В. В., Сканави М. И. Элементарная математика. Повторительный курс. — Издание третье, стереотипное. — М.: Наука, 1976. — 591 с.
Источник
Определение.
Ромб — это параллелограмм, который имеет равные стороны. Если у ромба все углы прямые, тогда он называется квадратом.
Ромбы отличаются между собой размером стороны и размером углов.
Признаки ромба
Параллелограмм ABCD будет ромбом, если выполняется хотя бы одно из следующих условий:
1. Две его смежные стороны равны (отсюда следует, что все стороны равны):
АВ = ВС = СD = AD
2. Его диагонали пересекаются под прямым углом:
AC┴BD
3. Одна из диагоналей (биссектриса) делит содержащие её углы пополам:
∠BAC = ∠CAD или ∠BDA = ∠BDC
4. Если все высоты равны:
BN = DL = BM = DK
5. Если диагонали делят параллелограмм на четыре равных прямоугольных треугольника:
Δ ABO = Δ BCO = Δ CDO = Δ ADO
6. Если в параллелограмм можно вписать круг.
Основные свойства ромба
2. Диагонали перпендикулярны:
AC┴BD
3. Диагонали являются биссектрисами его углов:
∠BAC = ∠CAD, ∠ABD = ∠DBC, ∠BCA = ∠ACD, ∠ADB = ∠BDC
4. Сумма квадратов диагоналей равна квадрату стороны умноженному на четыре:
AC2 + BD2 = 4AB2
5. Точка пересечения диагоналей называется центром симметрии ромба.
6. В любой ромб можно вписать окружность.
7. Центром окружности вписанной в ромб будет точка пересечения его диагоналей.
Сторона ромба
Формулы определения длины стороны ромба:
1. Формула стороны ромба через площадь и высоту:
2. Формула стороны ромба через площадь и синус угла:
3. Формула стороны ромба через площадь и радиус вписанной окружности:
4. Формула стороны ромба через две диагонали:
5. Формула стороны ромба через диагональ и косинус острого угла (cos α) или косинус тупого угла (cos β):
6. Формула стороны ромба через большую диагональ и половинный угол:
7. Формула стороны ромба через малую диагональ и половинный угол:
8. Формула стороны ромба через периметр:
Диагонали ромба
Определение.
Диагональю ромба называется любой отрезок соединяющий две вершины противоположных углов ромба.
Ромб имеет две диагонали – длинную d1, и короткую – d2
Формулы определения длины диагонали ромба:
1. Формулы большой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d1 = a√2 + 2 · cosα
d1 = a√2 – 2 · cosβ
2. Формулы малой диагонали ромба через сторону и косинус острого угла (cosα) или косинус тупого угла (cosβ)
d2 = a√2 + 2 · cosβ
d2 = a√2 – 2 · cosα
3. Формулы большой диагонали ромба через сторону и половинный угол:
d1 = 2a · cos(α/2)
d1 = 2a · sin(β/2)
4. Формулы малой диагонали ромба через сторону и половинный угол:
d2 = 2a · sin(α/2)
d2 = 2a · cos(β/2)
5. Формулы диагоналей ромба через сторону и другую диагональ:
d1 = √4a2 – d22
d2 = √4a2 – d12
6. Формулы диагоналей через тангенс острого tgα или тупого tgβ угла и другую диагональ:
d1 = d2 · tg(β/2)
d2 = d1 · tg(α/2)
7. Формулы диагоналей через площадь и другую диагональ:
8. Формулы диагоналей через синус половинного угла и радиус вписанной окружности:
Периметр ромба
Определение.
Периметром ромба называется сумма длин всех сторон ромба.
Длину стороны ромба можно найти за формулами указанными выше.
Формула определения длины периметра ромба:
Формула периметра ромба через сторону ромба:
P = 4a
Площадь ромба
Определение.
Площадью ромба называется пространство ограниченное сторонами ромба, т.е. в пределах периметра ромба.
Формулы определения площади ромба:
1. Формула площади ромба через сторону и высоту:
S = a · ha
2. Формула площади ромба через сторону и синус любого угла:
S = a2 · sinα
3. Формула площади ромба через сторону и радиус:
S = 2a · r
4. Формула площади ромба через две диагонали:
5. Формула площади ромба через синус угла и радиус вписанной окружности:
6. Формулы площади через большую диагональ и тангенс острого угла (tgα) или малую диагональ и тангенс тупого угла (tgβ):
Окружность вписанная в ромб
Определение.
Кругом вписанным в ромб называется круг, который примыкает ко всем сторонам ромба и имеет центр на пересечении диагоналей ромба.
Формулы определения радиуса круга вписанного в ромб:
1. Формула радиуса круга вписанного в ромб через высоту ромба:
2. Формула радиуса круга вписанного в ромб через площадь и сторону ромба:
3. Формула радиуса круга вписанного в ромб через площадь и синус угла:
4. Формулы радиуса круга вписанного в ромб через сторону и синус любого угла:
5. Формулы радиуса круга вписанного в ромб через диагональ и синус угла:
6. Формула радиуса круга вписанного в ромб через две диагонали:
7. Формула радиуса круга вписанного в ромб через две диагонали и сторону:
Источник
3. Геометрия на плоскости (планиметрия). Часть I
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Сумма внутренних углов любого четырехугольника равна (360^circ).

Свойства ромба:
(blacktriangleright) Те же, что и у параллелограмма:
(sim) Противоположные стороны попарно равны;
(sim) Диагонали точкой пересечения делятся пополам;
(sim) Противоположные углы попарно равны, а сумма соседних равна (180^circ);
(blacktriangleright) Диагонали взаимно перпендикулярны и являются биссектрисами углов ромба.
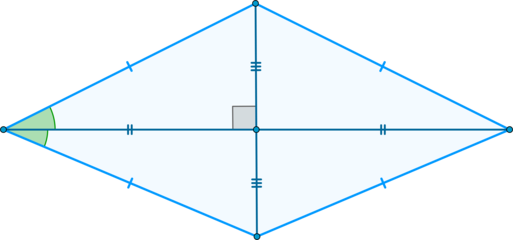
Признаки ромба.
Если для выпуклого четырехугольника выполнено одно из следующих условий, то это – ромб:
(blacktriangleright) все стороны равны;
(blacktriangleright) диагонали взаимно перпендикулярны и он является параллелограммом;
(blacktriangleright) диагонали являются биссектрисами углов и он является параллелограммом.
Площадь ромба
1. Т.к. ромб является параллелограммом, то для него верна та же формула площади. Таким образом, площадь ромба равна произведению высоты на основание, к которому эта высота проведена.

2. Площадь ромба равна половине произведения его диагоналей.

Задание
1
#2716
Уровень задания: Легче ЕГЭ
В ромбе (ABCD): (angle ACD = 26^{circ}). Найдите (angle ABD). Ответ дайте в градусах.
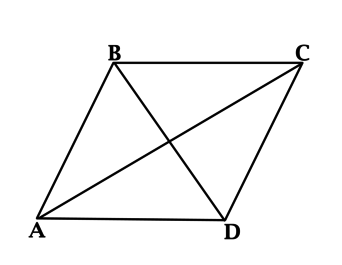
В ромбе диагонали перпендикулярны, тогда (angle CDB = 90^{circ} – angle ACD = 64^{circ}).
(BC = CD), тогда (angle CBD = angle CDB = 64^{circ}).
Так как диагонали ромба делят его углы пополам, то (angle ABD = angle CBD = 64^{circ}).
Ответ: 64
Задание
2
#2717
Уровень задания: Равен ЕГЭ
Найдите большую диагональ ромба (ABCD), если (AB = 2sqrt{3}), а острый угол равен половине тупого.

Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), то сумма острого и тупого углов ромба равна (180^{circ}).
Так как в данном ромбе острый угол равен половине тупого, то острый угол ромба (ABCD) равен (60^{circ}).
Треугольник (ABD) – равнобедренный, один из углов которого равен (60^{circ}), тогда треугольник (ABD) – равносторонний и (BD = 2sqrt{3}).
Пусть (O) – точка пересечения диагоналей ромба, тогда (OD = 0,5 BD = sqrt{3}), следовательно, по теореме Пифагора находим: (AO^2 + OD^2 = AD^2), тогда (AO^2 + 3 = 12), откуда находим (AO = 3). В ромбе, как и в любом другом параллелограмме, диагонали точкой пересечения делятся пополам, значит, (AC = 6).
Ответ: 6
Задание
3
#2715
Уровень задания: Равен ЕГЭ
Острый угол ромба (ABCD) равен (60^{circ}), одна из его сторон равна 10. Найдите меньшую из диагоналей этого ромба.
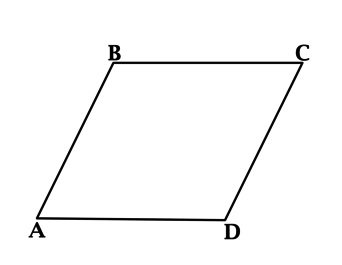
Пусть (angle A = 60^{circ}). В ромбе все стороны равны, тогда треугольник (ABD) – равнобедренный, у которого один из углов равен (60^{circ}), следовательно, треугольник (ABD) – равносторонний и (BD = 10).
Треугольник (ABC) – тупоугольный. В треугольнике против большего угла лежит большая сторона, тогда (AC > AB = BD), значит, (BD) – меньшая из диагоналей.
Ответ: 10
Задание
4
#1794
Уровень задания: Равен ЕГЭ
Расстояние от точки пересечения диагоналей ромба до одной из его сторон равно (3), а острый угол ромба равен (60^circ). Найдите большую диагональ ромба.
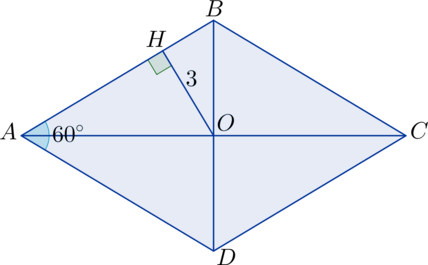
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), (angle DAB = 60^circ), тогда (angle
OAB = 30^circ). Получаем, что (OH) – катет лежащий напротив угла в (30^circ), значит (AO = 2cdot OH = 6). Т.к. (AC) и есть большая диагональ, то (AC = 2cdot AO = 12).
Ответ: 12
Задание
5
#1757
Уровень задания: Равен ЕГЭ
Сторона ромба равна (4). Расстояние от точки пересечения его диагоналей до одной из сторон равно (1). Найдите площадь ромба.
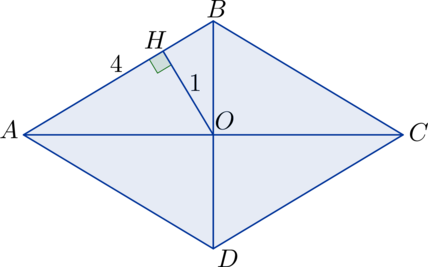
Пусть в ромбе (ABCD): (O) – точка пересечения диагоналей, (OH) – расстояние до стороны (AB), тогда (S_{triangle ABO} = frac{1}{2}cdot 1 cdot 4 = 2). Диагонали ромба делят его на (4) равных прямоугольных треугольника (Rightarrow) (S_{ABCD} = 4cdot 2 = 8).
Ответ: 8
Задание
6
#2718
Уровень задания: Равен ЕГЭ
Периметр ромба равен (40), а диагонали относятся, как (3:4). Найдите площадь ромба.
Половины диагоналей находятся в таком же отношении, как и диагонали, то есть в отношении (3:4). Зная периметр, найдем сторону ромба: (40
: 4 = 10). Сторона и половинки диагоналей образуют прямоугольный треугольник (AOB).
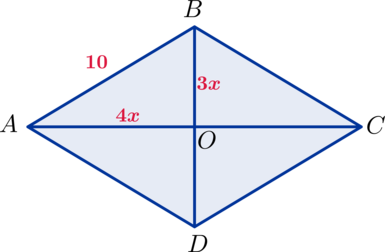
Пусть (AO=4x), (BO=3x).
Тогда по теореме Пифагора: ((3x)^2 + (4x)^2 = 10^2) (Rightarrow) (25x^2 = 100) (Rightarrow) (x^2 = 4) (Rightarrow) (x = 2). Диагонали равны (BD=2BO=12) и (AC=2AO=16) (Rightarrow) (S_{ABCD} =
frac{1}{2}cdot12cdot16 = 96).
Ответ: 96
Задание
7
#2719
Уровень задания: Равен ЕГЭ

Во сколько раз отличаются площади ромбов, имеющие по равному углу, у которых стороны относятся как (3:1)?
Пусть (angle B) и (angle B_1) – равные углы ромбов. Так как стороны ромбов относятся как (3:1), то можно обозначить их за (3x) и (x) соответственно.
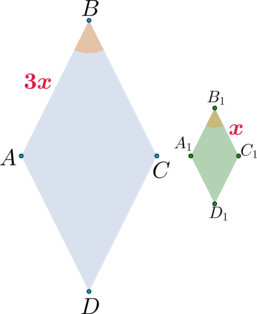
Тогда и (angle D=angle D_1) (так как у ромба противоположные углы равны). Следовательно, (triangle ABCsim triangle A_1B_1C_1) и (triangle ADCsimtriangle A_1D_1C_1) по двум пропорциональным сторонам и углу между ними, причем коэффициент подобия этих треугольников равен (3). Следовательно, их площади относятся как (9:1). А так как (S_{ABC}+S_{ADC}=S_{ABCD}) и (S_{A_1B_1C_1}+S_{A_1D_1C_1}=S_{A_1B_1C_1D_1}), то (S_1:S_2=9:1).
Ответ: 9
Геометрические задачи на тему «Свойства ромба» в обязательном порядке включаются в ЕГЭ по математике. Причем, в зависимости от условия задания, учащийся может давать как краткий, так и развернутый ответ. Именно поэтому на этапе подготовки к сдаче ЕГЭ школьникам непременно стоит понять принцип решения задач на применение свойств и признаков ромба.
Еще раз повторить данную тему и восполнить пробелы в знаниях вам поможет образовательный проект «Школково». С помощью нашего сайта можно легко и эффективно подготовиться к ЕГЭ по математике.
Чтобы успешно справляться с геометрическими заданиями, учащимся старших классов стоит повторить базовые понятия и определения: свойства углов ромба и других четырехугольников, признаки этой фигуры, а также формулу для нахождения ее площади. Данный материал представлен в разделе «Теоретическая справка» на сайте «Школково». Информация, которую подготовили наши специалисты, изложена в максимально доступной форме.
Повторив основные свойства диагоналей ромба, а также его углов и биссектрис, учащиеся могут попрактиковаться в выполнении упражнений. Большая подборка заданий по данной теме, а также по решению нестандартных задач по математике представлена в разделе «Каталог». Найти правильный ответ выпускники смогут, предварительно освежив в памяти свойства биссектрис ромба, в также углов и диагоналей этой фигуры. Подробный алгоритм решения каждой задачи прописан нашими специалистами.
Выполнять простые и более сложные задания по теме «Ромб и его свойства», а также на нахождение площади квадрата на этапе подготовки к ЕГЭ по математике школьники из Москвы и других городов могут в режиме онлайн. При необходимости любое упражнение можно сохранить в разделе «Избранное». Это позволит в дальнейшем быстро найти это задание и, к примеру, обсудить алгоритм его решения со школьным преподавателем.
Источник
