Какими свойствами обладает показательная функция
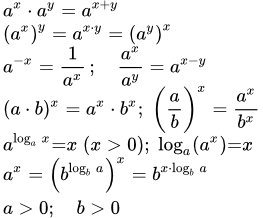
Приведены справочные данные по показательной функции – основные свойства, графики и формулы. Рассмотрены следующие вопросы: область определения, множество значений, монотонность, обратная функция, производная, интеграл, разложение в степенной ряд и представление посредством комплексных чисел.
Содержание
ОпределениеСвойства показательной функцииЧастные значенияГрафики показательной функцииВозрастание, убываниеОбратная функцияДифференцирование показательной функцииПроизводная показательной функцииПример дифференцирования показательной функцииИнтегралВыражения через комплексные числаРазложение в рядСм. также: Экспонента, е в степени х
Логарифм – свойства, формулы, график
Степенная функция и корни
Определение
Показательная функция – это обобщение произведения n чисел, равных a:
y(n) = an = a·a·a···a,
на множество действительных чисел x:
y(x) = ax.
Здесь a – фиксированное действительное число, которое называют основанием показательной функции.
Показательную функцию с основанием a также называют экспонентой по основанию a.
Обобщение выполняется следующим образом.
При натуральном x = 1, 2, 3,…, показательная функция является произведением x множителей:
.
При этом она обладает свойствами (1.5-8) (см. ниже ⇓), которые следуют из правил умножения чисел. При нулевом и отрицательных значениях целых чисел , показательную функцию определяют по формулам (1.9-10). При дробных значениях x = m/n рациональных чисел, , ее определяют по формуле(1.11). Для действительных , показательную функцию определяют как предел последовательности:
,
где – произвольная последовательность рациональных чисел, сходящаяся к x: .
При таком определении, показательная функция определена для всех , и удовлетворяет свойствам (1.5-8), как и для натуральных x.
Строгая математическая формулировка определения показательной функции и доказательство ее свойств приводится на странице «Определение и доказательство свойств показательной функции».
Свойства показательной функции
Показательная функция y = ax, имеет следующие свойства на множестве действительных чисел ():
(1.1) определена и непрерывна, при , для всех ;
(1.2) при a ≠ 1 имеет множество значений ;
(1.3) строго возрастает при , строго убывает при ,
является постоянной при ;
(1.4) при ;
при ;
(1.5) ;
(1.6) ;
(1.7) ;
(1.8) ;
(1.9) ;
(1.10) ;
(1.11) , .
Другие полезные формулы.
.
Формула преобразования к показательной функции с другим основанием степени:
При b = e, получаем выражение показательной функции через экспоненту:
Частные значения
, , , , .
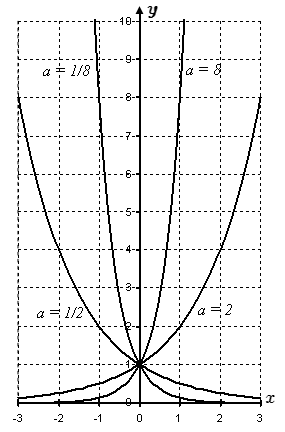
Графики показательной функции

Графики показательной функции y = ax при различных значениях основания a.
На рисунке представлены графики показательной функции
y(x) = a x
для четырех значений основания степени: a = 2, a = 8, a = 1/2 и a = 1/8. Видно, что при a > 1 показательная функция монотонно возрастает. Чем больше основание степени a, тем более сильный рост. При 0 < a < 1 показательная функция монотонно убывает. Чем меньше показатель степени a, тем сильнее убывание.
Возрастание, убывание
Показательная функция, при является строго монотонной, поэтому экстремумов не имеет. Основные ее свойства представлены в таблице.
| y = ax, a > 1 | y = ax, 0 < a < 1 | |
| Область определения | – ∞ < x < + ∞ | – ∞ < x < + ∞ |
| Область значений | 0 < y < + ∞ | 0 < y < + ∞ |
| Монотонность | монотонно возрастает | монотонно убывает |
| Нули, y = 0 | нет | нет |
| Точки пересечения с осью ординат, x = 0 | y = 1 | y = 1 |
| + ∞ | 0 | |
| 0 | + ∞ |
Обратная функция
Обратной для показательной функции с основанием степени a является логарифм по основанию a.
Если , то
.
Если , то
.
Дифференцирование показательной функции
Для дифференцирования показательной функции, ее основание нужно привести к числу e, применить таблицу производных и правило дифференцирования сложной функции.
Для этого нужно использовать свойство логарифмов
и формулу из таблицы производных:
.
Пусть задана показательная функция:
.
Приводим ее к основанию e:
Применим правило дифференцирования сложной функции. Для этого вводим переменную
Тогда
Из таблице производных имеем (заменим переменную x на z):
.
Поскольку – это постоянная, то производная z по x равна
.
По правилу дифференцирования сложной функции:
.
Производная показательной функции
.
Производная n-го порядка:
.
Вывод формул > > >
Пример дифференцирования показательной функции
Найти производную функции
y = 35x
Решение
Выразим основание показательной функции через число e.
3 = e ln 3
Тогда
.
Вводим переменную
.
Тогда
Из таблицы производных находим:
.
Поскольку 5ln 3 – это постоянная, то производная z по x равна:
.
По правилу дифференцирования сложной функции имеем:
.
Ответ
Интеграл
.
Выражения через комплексные числа
Рассмотрим функцию комплексного числа z:
f(z) = a z
где z = x + iy; i2 = – 1.
Выразим комплексную постоянную a через модуль r и аргумент φ:
a = r e i φ
Тогда
.
Аргумент φ определен не однозначно. В общем виде
φ = φ0 + 2πn,
где n – целое. Поэтому функция f(z) также не однозначна. Часто рассматривают ее главное значение
.
Разложение в ряд
.
Использованная литература:
И.Н. Бронштейн, К.А. Семендяев, Справочник по математике для инженеров и учащихся втузов, «Лань», 2009.
Автор: Олег Одинцов. Опубликовано: 21-02-2014 Изменено: 19-11-2018
См. также: Экспонента, е в степени х
Логарифм – свойства, формулы, график
Степенная функция и корни
Источник
Общие сведения
Функцией называется закон зависимости одной величины от другой. Выражается она при помощи выражений алгебраического, тригонометрического, иррационального и других типов. Существует два типа переменных, которые встречаются в любых функциях: зависимая и независимая. Последняя называется также аргументом.
Основной особенностью показательной функции считается ее вид, поскольку основанием является число, а степенью — аргумент. Последним называется независимая переменная, которая может принимать любые значения, кроме превращающих ее значение в пустое множество или неопределенность. Показательной называется функция вида z (y) = a^y (a > 0), которая зависит от аргумента в виде показателя степени «y».
Сферы использования
Применяется в описании различных законов роста какой-либо величины. В зависимости от показателя, функция может быстро возрастать. Иногда вместо основания «а» может быть указан символ экспоненты, которая стремительно возрастает. Пример показательной функции mc (t) = m0 * (½)^(t/T) используется при подсчете энергии, выделяемой во время деления ядер радиоактивного элемента за время t. Переменные и коэффициенты расшифровываются следующим образом:
- Масса радиоактивного вещества — зависимая переменная «mc (t)» от аргумента «t».
- Постоянная «m0» — начальная масса.
- Значение «Т» — период полураспада радиоактивного элемента.
Скорость роста функции можно проиллюстрировать на примере шахматной доски с зернами пшеницы. История гласит, что изобретатель шахмат попросил в награду положить на 1 клетку 1 зерно, на вторую — 2, на третью — 2 * 2 = 4 и так далее. На последнюю положили 2 63 штуки злаковых зерен. Следует отметить, что на шахматной доске 64 клетки. Решение простое, но результат вычисляется затруднительно, поскольку следует посчитать значение 1 + 2 + 2 2 + 2 3 + … + 2 63 .
Используя формулу геометрической прогрессии Sn = b1 * [(q^n) — 1] / (q — 1), можно без проблем вычислить значение. Первое значение b1 = 1, знаменатель q = 2 3 / 2 2 = 2 2 / 2 = 2 / 1 = 2. Общее число зерен определяется таким образом: S64 = 1 * [(2 64 ) — 1] / (2 — 1) = (2 64 ) — 1. Ученые подсчитали, что такое количество превышает урожай пшеницы на планете за 2008−2009 год в 1800 раз. Если воспользоваться справочником или компьютером, то S64 = 18446744073709551615 — 1 = 18446744073709551614.
Примеры иллюстрируют применение степенной функции в жизни, поскольку она может описывать явления природы, в которой протекают различные процессы. Например, деление клеток злокачественных опухолей, увеличение количества молекул озона при разрядах молнии и так далее.
Представление функции
Математики рекомендуют ознакомиться на начальных этапах с графиком показательной функции и ее свойствами. Графиком называется ее графическое представление в некоторой системе координат. В качестве последней распространена декартовая прямоугольная с двумя осями (ординат — z и абсцисс — y). Оси можно обозначать любыми литерами. Например, в формуле mc (t) = m0 * (½)^(t/T) рекомендуется использовать в качестве ординаты ось «mc», а абсциссой будет время t.
Необходимо рассмотреть свойства функции, а затем строить ее график. Они различаются между собой, поскольку существует несколько вариантов представления. Для правильного построения и анализа необходимо разобрать все варианты. Это позволит воспользоваться уже готовым материалом и существенно оптимизирует процесс решения задач. Представление функции состоит из свойств и графика.
Основные свойства
Свойствами функции z = a^y называется совокупность некоторых характеристик, присущих только ей. Они нужны не только для построения графика, но и для дифференцирования, анализа и интегрирования. Список свойств и полезных соотношений:
- Область определения показательной функции D (z): все действительные числа R (-inf;+inf).
- Множество значений E (z): (0;+inf).
- Минимальное и максимальное значения отсутствуют.
- Принадлежит к функциям общего вида, то есть не является четной и нечетной.
- Периодичность: отсутствует.
- Пересечение с осью ординат: точка с координатами (0;1).
- Нулевые значения: отсутствуют.
- При а > 0 функция возрастает. Когда 0 < a < 1, тогда она будет убывать.
- На всей D (z) принимает только положительные значения.
- Неопределенность или пустое множество: 0 0 и y < 0 (при а = 0).
- Если y принимает отрицательные значения y < 0, то выполняется такое соотношение: a^y = 1 / (a^|y|). Обозначение «|y|» — модуль аргумента, который принимает только положительные значения.
- a 0 = 1.
- a^(w + f) = (a^w) * (a^f).
- (a^w)^f = a^(w * f).
- (a * b)^y = (a^y) * (b^y).
- Когда b не равно нулю: (a / b)^y = (a^y) / (b^y).
- a^(m/n) = [a^m]^(1/n) = [a^(1/n)]^m.
- Представление через логарифм по основанию «а» (y > 0): a^(log (y)|a) = y.
- Формула преобразования в функцию с другим основанием «b»: a^y = [b^(log (a)|b)]^y = b^[y * log (a)|b)].
- Если b = e (экспонента), то показательную функцию можно выразить через натуральный логарифм таким образом: a^y = e^(y * ln (a)).
Свойства функции доказываются математическим путем. Они основаны на алгоритмах исследования ее поведения.
Доказательства некоторых утверждений
Соотношения необходимы для решения различных задач, основанных на дифференцировании, интегрировании и упрощении выражений. Можно доказать третье свойство, то есть попытаться найти минимум и максимум. Для нахождения экстремумов следует воспользоваться таким алгоритмом:
- Найти производную: [a^y]’ = a^y * ln (a).
- Производная существует во всех точках, кроме следующих: при x = 0 (a = 0), x < 0 (а = 0) и a > 0.
- Поиск стационарных точек [a^y]’ = 0: a^y * ln (a) = 0. Решений нет, поскольку a^y не может принимать нулевое значение.
- Вывод: минимального и максимального значений нет вообще.
Проверка на четность осуществляется по соотношению z (-y) = z (y) таким образом: a^(-y) = 1 / |a^y|. Правая часть тождества не соответствует левой. Значит можно сделать вывод, что z (y) не является четной. Чтобы проверить на нечетность, следует воспользоваться равенством z (-y) = -z (y). Подставив значение «-у», получается следующее: a^(-y) = 1 / |a^y|. Следовательно, функция принадлежит к общему виду, то есть правилам четности и нечетности она не подчиняется.
Точка пересечения с осью ординат рассчитывается таким образом: решается уравнение z = a^y относительно y, принимающего нулевое значение: z = a 0 = 1. Искомая точка имеет координаты (0;1).
Построение графиков
Для построения графиков следует рассмотреть два случая, при которых a > 0 (рис. 1) и 0 < a < 1 (рис. 2). Кроме того, можно для сравнения построить частные примеры со следующими условиями:
- a < 0 и x > 0 (рис. 3).
- a = 0 и x > 0 (рис. 4).
- a = 1 и x > 0 (рис. 5).
Для построения графика существуют свои правила, которых рекомендуют придерживаться математики. Процедура осуществляется в двух режимах: схематическом и точном. В первом случае нужно знать свойства. Таблица зависимостей значения от аргумента не составляется. При точном построении необходимо составить таблицу. В ней необходимо рассмотреть около 5-10 значений независимой переменной. Затем все точки отмечаются на декартовой системе координат и плавно соединяются.
Оформление играет очень важную роль, поскольку не допускаются исправления. Очень важно соблюдать масштаб, и не отмечать каждое значение шкалы делений на оси абсцисс и ординат. Следует учитывать, что графики чертят также в двух режимах: автоматизированном и ручном. В первом случае применяются специализированные программы и веб-приложения (онлайн-калькуляторы). В последнем необходимо чертить карандашом, используя линейку. Этот момент очень важен, поскольку приучает к дисциплине на уроках, а также повышает читабельность материала. Для примера нужно начертить график z = 2^y. Необходимо составить таблицу 1:
| z | 0,3 | 0,5 | 1 | 2 | 4 | 8 |
| у | -2 | -1 | 0 | 1 | 2 | 3 |
Таблица 1. Зависимость значения от аргумента (z = 2^y).
По таблице нужно построить график, отмечая координаты каждой из точек. После этого нужно плавно их соединить. Должен получиться примерно такой график:
Рисунок 1. График z = 2^y (a > 0 и y > 0).
Если рассмотреть пример, в котором y > 0 и 0 < a < 1, то графическое изображение (рис. 2) будет немного другим:
Рисунок 2. График при 0 < a < 1.
При a < 0 и x > 0 график также существенно изменится, поскольку будет постоянно убывать:
Рисунок 3. Графическая иллюстрация при a < 0 и x > 0.
Когда основание равно 0, тогда функция перестает быть показательной, поскольку не соблюдается условие из определения. На рисунке 4 представлен ее график:
Рисунок 4. Графическое представление при a = 0 и x > 0.
Последний случай — основание равно 1. Функция также не является показательной.
Рисунок 5. График при a = 1 и x > 0.
Кроме того, встречаются задачи не только на построение графика, но и на осуществление операций дифференцирования, нахождения производной и первообразной.
Правила дифференцирования
В некоторых задачах следует найти производную или дифференциал степенной функции. Для осуществления этой операции существует определенный алгоритм, который специалисты рекомендуют рассмотреть на конкретном примере. Условие задачи следующее: найти дифференциал z = 4^(6y). Для его нахождения нужно предпринять такие шаги:
- Выразить через основание “e”: 4 = e^(ln4).
- Подставить в исходную функцию (следует воспользоваться 20 свойством): z = 4^(6y) = e^[ln(4 * 6 * y] = e^[6ln(4y)].
- Ввести новую переменную t = [6ln(4y)]: z = e^t.
- Воспользовавшись таблицей производных, найти значение функции в третьем пункте: z’ = [e^t]’ = e^t.
- Дифференциал находится по такой формуле: dz / dy = (dz / dt) * (dt / dy) = (e^t) * 6ln(4) = [4^(6y)] * 6ln(4).
Необходимо отметить, что производная берется из таблицы простейших (элементарных) функций. Когда выражение является сложным, как в примере, то дифференциал ищется по частям. Формула для сложного выражения имеет такой вид: [w(y(z(x)))]’ = [z(x)]’ * [y(z(x))]’ * [w(y(z(x)))]’. Соотношение трудно понять, но на примере все довольно просто. Например, нужно найти производную z = e^(2cos(2x^2 + 1)). Функция состоит из трех элементов: f = 2x^2 + 1, y = 2cos(f) и v = e^y.
Следует воспользоваться формулой и вычислить производную каждого элемента: z’ = [e^(2cos(2x^2 + 1))]’ = 2[2x^2 + 1]’ * [cos(f)]’ * [e^y]’ = 8x * (-sin(2x^2 + 1)) * e^(2cos(2x^2 + 1)). Результат следует оставить в таком виде, поскольку подобных слагаемых нет. Однако математики рекомендуют выносить минус в начало выражения: z’ = -8x * (sin(2x^2 + 1)) * e^(2cos(2x^2 + 1)).
Поиск первообразных
Отдельным классом задач является интегрирование или нахождение первообразных. Для этой цели применяются специальные таблицы интегралов простейших функций. Кроме того, можно воспользоваться и табличными значениями производных. Они позволяют найти искомое первообразное выражение. Интегрирование считается обратной операцией и позволяет найти тождество, из которого была получена производная.
Для нахождения интеграла a^y следует воспользоваться такой формулой: ∫(a^y)dy = ∫(e^(ln(a * y))dy = [1 / ln(a)] * ∫(e^(ln(a * y))d(ln(a * y) = [1 / ln(a)] * (e^(ln(a * y)) + C = [1 / ln(a)] * (a^y) + C. Коэффициент «С» — константа, которая при дифференцировании исчезает. Однако ее необходимо учитывать. Кроме того, необходимо постоянно следить за знаком интеграла и переменной, по которой находится первообразная.
Таким образом, для решения задач со степенной функцией нужно пользоваться свойствами и алгоритмами, поскольку это существенно сэкономит время и избавит от множества ошибок.
Источник
Определение и свойства
Определение
Показательная функция f(n) = an, с основанием a, от натурального аргумента n – это произведение n множителей, каждый из которых равен a:
.
Здесь .
При она обладает следующими свойствами, вытекающих из правил умножения чисел:
(1.1) a x> 0 при a > 0;
(1.2) строго возрастает при a > 1 и строго убывает при 0 < a < 1;
(1.3) ;
(1.4) ;
(1.5) .
Если положить:
(1.6) ,
(1.7) ,
то показательная функция становится определенной и для целых чисел. При этом свойства (1.1-5) по прежнему выполняются, в которых , . Подробнее ⇓
Если положить:
(1.8) ,
где , то показательная функция становится определенной и для рациональных чисел . При этом выполняются свойства (1.1-7). В них , . Подробнее ⇓
Далее, основываясь на свойствах показательной функции (1.1-8), определенной на множестве рациональных чисел, мы определяем эту функцию на множестве действительных чисел и даем доказательство ее свойств.
Лемма
Пусть последовательность рациональных чисел сходится к действительному числу x:
.
И пусть a > 0. Тогда существует предел последовательности :
,
и этот предел может зависеть от числа x, но не зависит от последовательности .
Доказательство ⇓
Определение показательной функции
Показательная функция f(x) = ax, с основанием a > 0 – это предел последовательности
,
где есть произвольная последовательность рациональных чисел, стремящаяся к x:
.
Это определение справедливо и в случае, если x является рациональным числом. При этом совпадает со значением показательной функции, определяемом на множестве рациональных чисел. Чтобы убедиться в этом, достаточно в качестве последовательности взять последовательность с постоянными членами .
Заметим, что для доказательства свойств показательной функции, нам достаточно выбрать любую, удобную для нас последовательность рациональных чисел , сходящуюся к x. Действительно, согласно лемме ⇑, значение не зависит от выбора последовательности.
Теорема. Свойства показательной функции
Показательная функция имеет на множестве действительных чисел x следующие свойства:
(2.0) определена, при , для всех ; ⇓
(2.1) при a ≠ 1 имеет множество значений ; ⇓
(2.2) строго возрастает при , строго убывает при , является постоянной при ; ⇓
(2.3) ; ⇓
(2.3*) ; ⇓
(2.4) ; ⇓
(2.5) ; ⇓
(2.5*) ; ⇓
(2.6) ; ⇓
(2.7) ; ⇓
(2.8) непрерывна для всех ; ⇓
(2.9) при ;
при . ⇓
Доказательство ⇓
Определение показательной функции на множестве целых чисел
Исследуем вопрос – что будет, если для функции, обладающей свойствами (1.3-5), присвоить отрицательные значения аргумента? Положим
.
Умножим это уравнение на и воспользуемся свойством (1.3):
.
Поскольку , то мы получаем:
.
Отсюда , или
.
В частности, .
Таким образом, свойства (1.3-5) выполняются для отрицательных и нулевого значения n, если положить:
;
.
Тем самым мы определили значения показательной функции для целых чисел. Однако это возможно не для всех значений основания a. Поскольку деление на нуль не возможно, то .
Определение показательной функции на множестве рациональных чисел
Теперь рассмотрим вопрос об определении показательной функции для рациональных значений аргумента. Пусть есть рациональное число. Его можно представить в виде дроби:
,
где – целое, – натуральное.
Возьмем самый простой случай. Пусть . Рассмотрим уравнение:
.
Умножим его левую и правую части на себя n раз. То есть возведем в степень n и применим свойство (1.4):
;
(3.1) .
Таким образом, есть корень степени n из a:
.
Для любого и для , существует единственное решение уравнения (3.1) в области действительных чисел (см. «Доказательство существования и единственности корня степени n»).
Далее мы используем свойства корней:
(3.2) ;
(3.3) .
(3.4) .
В силу свойства (3.2), мы можем определить значения показательной функции для рациональных значений аргумента:
.
Используя свойства (1.3-7) для целых значений аргумента и свойства корней (3.2-4), можно доказать, что (1.3-7) выполняются и для рациональных значений аргумента показательной функции.
Доказательство леммы и свойств показательной функции
Лемма
Пусть последовательность рациональных чисел сходится к действительному числу x:
.
И пусть a > 0. Тогда существует предел последовательности :
,
и этот предел может зависеть от числа x, но не зависит от последовательности .
Доказательство
1. Докажем существование предела
.
Поскольку последовательность сходится, то для нее выполняется условие Коши. Это означает, что имеется такая функция , при которой для любого выполняется неравенство:
(Л.1) при .
Подставим . Тогда
(Л.2) при .
1.1. Пусть .
Докажем, что условие Коши выполняется для последовательности . Применим лемму Бернулли. При имеем:
(Л.3) .
Поскольку последовательность сходится к конечному числу, то она ограничена некоторым числом :
для всех n.
Поскольку показательная функция, определенная на множестве рациональных чисел строго возрастает при a > 1, то
для всех m.
Обозначим . В силу свойства (1.1), . Подставим в (Л.3) и применим условие Коши (Л.1). При имеем:
.
Если положить , то
при .
Итак, мы нашли такую функцию , при которой для любого ,
при .
То есть выполняется условие Коши для последовательности . Тогда на основании критерия Коши, эта последовательность сходится.
1.2. Теперь рассмотрим случай . Сведем его к предыдущему. Положим . Тогда , . Мы доказали, что последовательность сходится. Единицу в числителе можно рассматривать как элемент последовательности с постоянными членами, равными 1. Тогда, на основании арифметических свойств, существует предел частного последовательностей .
2. Теперь докажем, что предел не зависит от выбора последовательности .
Пусть мы имеем две, сходящиеся к x, последовательности и :
.
Мы доказали, что существуют пределы
и .
Теперь нам нужно доказать, что .
Составим последовательность так, чтобы последовательности и являлись ее подпоследовательностями. Для нечетных n, положим ; для четных: . Последовательность имеет предел . Тогда, согласно доказанному выше, существует предел . Далее замечаем, что последовательности и являются подпоследовательностями последовательности . Поскольку предел любой подпоследовательности равен пределу последовательности, то
.
Лемма доказана.
Доказательство теоремы – свойства показательной функции
Формулировка ⇑
Порядок доказательств свойств показательной функции отличается от порядка, в котором расположены свойства. Это сделано для удобства изложения. Последующие пункты могут использовать свойства, доказанные в первую очередь.
2.А. Сначала докажем, что
(2.А.1) ax> 0.
Согласно определению ⇑,
.
Поскольку последовательность рациональных чисел сходится к конечному числу x, то она ограничена:
.
Поскольку функция , определенная на множестве рациональных чисел монотонна (см. (1.2) ⇑ ), то она достигает своего минимального значения на границе рассматриваемого отрезка. Тогда
(2.А.2) .
Здесь при нужно взять знак “плюс”. При – знак “минус”. При , функция постоянна, . Можно взять любой знак. Выполним в (2.А.2) предельный переход , пользуясь свойствами пределов последовательностей, связанными неравенствами и определением показательной функции ⇑:
;
.
Согласно свойству (1.1) ⇑, . Тогда и
.
2.0. ⇑ Докажем, что показательная функция
определена, при , для всех действительных чисел .
Поскольку показательная функция , при , определена для всех рациональных чисел r ⇑, и поскольку для любого действительного числа x существует последовательность рациональных чисел, сходящихся к x, то, согласно определению ⇑, показательная функция определена для всех действительных чисел .
2.6. ⇑ Докажем, что
.
Здесь аргумент является рациональным числом. Мы считаем, что свойства показательной функции на множестве рациональных чисел известны. Мы добавили пункт 2.6, чтобы объединить все свойства вместе.
2.2. ⇑ Докажем строгую монотонность показательной функции при a ≠ 1. То есть, если , то
при ;
при ;
при .
Итак, пусть . Выберем рациональные числа и , удовлетворяющие неравенствам:
.
Возьмем последовательности и , сходящиеся к и :
,
элементы которых удовлетворяют неравенствам:
, .
Тогда
.
2.2.1. Пусть .
Поскольку показательная функция, определенная на множестве рациональных чисел, при , строго возрастает, то
(2.2.1) .
Применим свойства пределов последовательностей, связанных неравенствами и определение показательной функции ⇑:
;
.
Отсюда .
2.2.2. Пусть .
В этом случае, показательная функция, определенная на множестве рациональных чисел, строго убывает. Доказательство такое же, как и в пункте 2.2.1, только начиная с (2.2.1), нужно поменять знаки неравенств:
(2.2.2) ;
;
;
.
2.2.3. Пусть .
Показательная функция , определенная на множестве рациональных чисел , является постоянной . Последовательность является последовательностью из постоянных элементов. Поэтому ее предел также равен единице:
;
для всех x.
2.3. ⇑ Докажем, что
.
Пусть и – произвольные последовательности рациональных чисел, сходящиеся к и :
.
Применим свойство предела суммы для последовательности :
(2.3.1) .
Рассмотрим последовательность . Поскольку, согласно лемме ⇑, и сходятся, то применим свойство предела произведения последовательностей иопределение показательной функции ⇑:
.
С другой стороны, применяя (2.3.1) и свойство (1.3) ⇑ показательной функции от рационального аргумента, имеем:
.
Отсюда
.
2.5. ⇑ Докажем, что
.
Все рассуждения и обозначения такие же, что и при доказательстве свойства (2.3) ⇑. Аналогичным образом, применяя свойство (1.5) ⇑ для рационального аргумента, имеем:
.
2.7. ⇑ Докажем, что
.
Аналогично предыдущему, имеем:
.
Здесь мы учли, что и применили свойство предела частного последовательностей.
2.3*. ⇑ Докажем, что
.
Применяя свойства (2.3) ⇑ и (2.7) ⇑, имеем:
.
2.4. ⇑ Докажем, что
.
2.4.1. Рассмотрим случай .
Пусть – натуральные числа. Тогда
.
Применяя свойство (2.3) ⇑, имеем:
;
(2.4.1) .
Теперь исследуем, что такое . Введем обозначение:
(2.4.2) .
Возведем в n-ю степень. То есть умножим левую и правую части на себя n раз, и применим (2.4.1):
;
.
Поскольку ax> 0 ⇑, то b есть корень степени n из положительного числа :
. Подставляя (2.4.2), имеем:
(2.4.3) .
Применяя свойства (2.4.1) и (2.4.3), для произвольного положительного рационального числа получаем:
;
(2.4.4) .
Пусть есть произвольная последовательность рациональных чисел, сходящаяся к x2:
(2.4.5) .
Применем (2.4.4):
.
Рассмотрим последовательность . Учитывая (2.4.5), и применяя арифметические свойства сходящихся последовательностей, получаем, что сходится к :
.
Выше мы доказали, что показательная функция непрерывна ⇑. Используя определение непрерывности функции по Гейне, получаем:
;
.
Что и требовалось доказать.
2.4.2. Рассмотрим случай .
Тогда . Применяя свойство (2.7) ⇑, имеем:
.
2.4.3. Теперь пусть .
Применяем (2.6) ⇑ Тогда .
Поскольку ax1> 0 ⇑, то
.
Таким образом и в этом случае
.
2.5*. ⇑ Докажем, что
.
Применяя свойства (2.5) ⇑, (2.4) ⇑ и (2.7) ⇑, имеем:
.
2.8. ⇑ Докажем, что показательная функция
непрерывна для всех .
2.8.1. Пусть .
Воспользуемся определением непрерывности функции в терминах приращений. Применяем свойство ax> 0 ⇑ и (2.3) ⇑
.
Поскольку есть сколь угодно малая величина, то считаем, что . Применим лемму Бернулли для действительных чисел:
.
Тогда
.
Применяем свойство пределов функций, связанных неравенством:
;
;
.
2.8.2. Пусть .
Введем число . Тогда .
Воспользуемся свойством (2.5*) ⇑ и учтем, что – постоянная функция:
.
Рассмотрим функцию как сложную, составленную из двух функций:
. Выше мы доказали, что функция непрерывна для всех x. Функция непрерывна при . Это можно доказать, применяя арифметические свойства предела функции:
.
Выше мы доказали ⇑, что . Тогда согласно теореме о непрерывности сложной функции, функция непрерывна для всех x.
2.8.3. Пусть .
Выше мы показали ⇑, что функция является постоянной функцией: . Поэтому она является непрерывной для всех x.
2.9. ⇑ Докажем, что
при ;
при .
2.9.1. Пусть .
2.9.1.1. Докажем, что
.
Поскольку функция монотонна ⇑, то согласно теореме о пределе монотонной функции, она имеет конечный или бесконечный предел
.
Поскольку функция имеет предел A, то согласно определению предела функции по Гейне, для любой последовательности , сходящейся к , последовательность сходится к A:
.
Возьмем последовательность натуральных чисел . Она сходится к : . Тогда
.
Для вычисления этого предела, применим неравенство Бернулли:
.
При , правая часть неравенства стремится к . Применяя свойство неравенств бесконечно больших последовательностей, находим, что
.
Отсюда , .
2.9.1.2. Докажем, что
.
Сделаем подстановку . Применим свойство (2.7) ⇑ и свойства бесконечно малых и бесконечно больших функций:
.
2.9.2. Пусть .
Сделаем подстановку . Тогда ,
;
.
2.1. ⇑ Докажем, что при a ≠ 1 показательная функция имеет множество значений .
Рассмотрим функцию на отрезке , где – произвольные числа. Поскольку функция строго монотонна ⇑ и определена для всех x, то она достигает минимума и максимума на концах отрезка – в точках и . Поскольку функция непрерывна ⇑, то согласно теореме Больцано – Коши о промежуточном значении, она принимает все значения из отрезка , если и , если . Устремляя и , и используя найденные выше пределы ⇑ получаем, что множеством значений показательной функции является множество положительных чисел .
Теорема доказана.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: 17-11-2018 Изменено: 31-10-2020
Источник
