Какими свойствами обладает параллелограмм
Определение.
Параллелограмм – это четырехугольник у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Параллелограммы отличаются между собой как размером прилегающих сторон, так и углами, однако противоположные углы одинаковые.
Признаки параллелограмма
Четырехугольник ABCD будет параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Четырехугольник имеет две пары параллельных сторон:
AB||CD, BC||AD
2. Четырехугольник имеет пару параллельных и равных сторон:
AB||CD, AB = CD (или BC||AD, BC = AD)
3. В четырехугольнике противоположные стороны попарно равны:
AB = CD, BC = AD
4. В четырехугольнике противоположные углы попарно равны:
∠DAB = ∠BCD, ∠ABC = ∠CDA
5. В четырехугольнике диагонали точкой пересечения делятся пополам:
AO = OC, BO = OD
6. Сумма углов четырехугольника прилегающих к любой стороне равна 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
7. В четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон:
AC2 + BD2 = AB2 + BC2 + CD2 + AD2
Основные свойства параллелограмма
Квадрат, прямоугольник и ромб – есть параллелограммом.
1. Противоположные стороны параллелограмма имеют одинаковую длину:
AB = CD, BC = AD
2. Противоположные стороны параллелограмма параллельны:
AB||CD, BC||AD
3. Противоположные углы параллелограмма одинаковые:
∠ABC = ∠CDA, ∠BCD = ∠DAB
4. Сумма углов параллелограмма равна 360°:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
5. Сумма углов параллелограмма прилегающих к любой стороне равна 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
6. Каждая диагональ делит параллелограмма на два равных треугольника
7. Две диагональ делят параллелограмм на две пары равных треугольников
8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:
| AO = CO = | d1 |
| 2 | |
| BO = DO = | d2 |
| 2 |
9. Точка пересечения диагоналей называется центром симметрии параллелограмма
10. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
AC2 + BD2 = 2AB2 + 2BC2
11. Биссектрисы противоположных углов параллелограмма всегда параллельны
12. Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)
Стороны параллелограмма
Формулы определения длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:
a =
√d12 + d22 – 2d1d2·cosγ2 =
√d12 + d22 + 2d1d2·cosδ2
b =
√d12 + d22 + 2d1d2·cosγ2 =
√d12 + d22 – 2d1d2·cosδ2
2. Формула сторон параллелограмма через диагонали и другую сторону:
3. Формула сторон параллелограмма через высоту и синус угла:
4. Формула сторон параллелограмма через площадь и высоту:
Диагонали параллелограмма
Определение.
Диагональю параллелограмма называется любой отрезок соединяющий две вершины противоположных углов параллелограмма.
Параллелограмм имеет две диагонали – длинную d1, и короткую – d2
Формулы определения длины диагонали параллелограмма:
1. Формулы диагоналей параллелограмма через стороны и косинус угла β (по теореме косинусов)
d1 = √a2 + b2 – 2ab·cosβ
d2 = √a2 + b2 + 2ab·cosβ
2. Формулы диагоналей параллелограмма через стороны и косинус угла α (по теореме косинусов)
d1 = √a2 + b2 + 2ab·cosα
d2 = √a2 + b2 – 2ab·cosα
3. Формула диагонали параллелограмма через две стороны и известную другую диагональ:
d1 = √2a2 + 2b2 – d22
d2 = √2a2 + 2b2 – d12
4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:
| d1 = | 2S | = | 2S |
| d2·sinγ | d2·sinδ |
| d2 = | 2S | = | 2S |
| d1·sinγ | d1·sinδ |
Периметр параллелограмма
Определение.
Периметром параллелограмма называется сумма длин всех сторон параллелограмма.
Формулы определения длины периметра параллелограмма:
1. Формула периметра параллелограмма через стороны параллелограмма:
P = 2a + 2b = 2(a + b)
2. Формула периметра параллелограмма через одну сторону и две диагонали:
P = 2a + √2d12 + 2d22 – 4a2
P = 2b + √2d12 + 2d22 – 4b2
3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:
Площадь параллелограмма
Определение.
Площадью параллелограмма называется пространство ограниченный сторонами параллелограмма, т.е. в пределах периметра параллелограмма.
Формулы определения площади параллелограмма:
1. Формула площади параллелограмма через сторону и высоту, проведенную к этой стороне:
S = a · ha
S = b · hb
2. Формула площади параллелограмма через две стороны и синус угла между ними:
S = ab sinα
S = ab sinβ
3. Формула площади параллелограмма через две диагонали и синус угла между ними:
Источник
Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
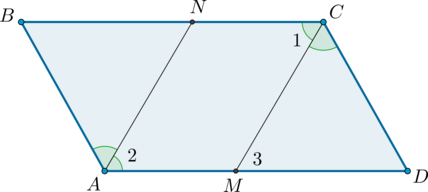
Пусть в четырехугольнике (ABCD) стороны (AB) и (CD) параллельны и (AB = CD).

Проведём диагональ (AC), разделяющую данный четырехугольник на два равных треугольника: (ABC) и (CDA). Эти треугольники равны по двум сторонам и углу между ними ((AC) – общая сторона, (AB = CD) по условию, (angle 1 = angle 2) как накрест лежащие углы при пересечении параллельных прямых (AB) и (CD) секущей (AC)), поэтому (angle 3 = angle 4). Но углы (3) и (4) накрест лежащие при пересечении прямых (AD) и (BC) секущей (AC), следовательно, (ADparallel BC). Таким образом, в четырехугольнике (ABCD) противоположные стороны попарно параллельны, и, значит, четырехугольник (ABCD) – параллелограмм.
Теорема (второй признак параллелограмма)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Проведём диагональ (AC) данного четырехугольника (ABCD), разделяющую его на треугольники (ABC) и (CDA).

Эти треугольники равны по трем сторонам ((AC) – общая, (AB = CD) и (BC = DA) по условию), поэтому (angle 1 = angle 2) – накрест лежащие при (AB) и (CD) и секущей (AC). Отсюда следует, что (ABparallel CD). Так как (AB = CD) и (ABparallel CD), то по первому признаку параллелограмма четырёхугольник (ABCD) – параллелограмм.
Теорема (третий признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
Рассмотрим четырехугольник (ABCD), в котором диагонали (AC) и (BD) пересекаются в точке (O) и делятся этой точкой пополам.
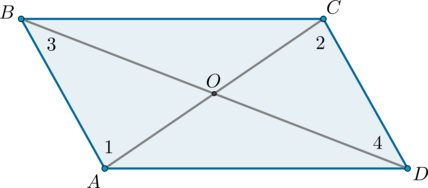
Треугольники (AOB) и (COD) равны по первому признаку равенства треугольников ((AO = OC), (BO = OD) по условию, (angle AOB = angle
COD) как вертикальные углы), поэтому (AB = CD) и (angle 1 = angle
2). Из равенства углов (1) и (2) (накрест лежащие при (AB) и (CD) и секущей (AC)) следует, что (ABparallel CD).
Итак, в четырехугольнике (ABCD) стороны (AB) и (CD) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник (ABCD) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.
Доказательство
1) Пусть (ABCD) – параллелограмм, (AE) – биссектриса угла (BAD).
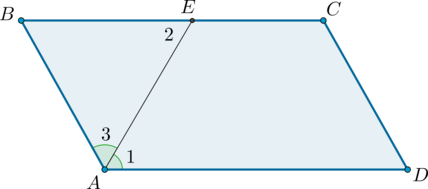
Углы (1) и (2) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (AE). Углы (1) и (3) равны, так как (AE) – биссектриса. В итоге (angle 3 = angle 1 = angle 2), откуда следует, что треугольник (ABE) – равнобедренный.
2) Пусть (ABCD) – параллелограмм, (AN) и (BM)– биссектрисы углов (BAD) и (ABC) соответственно.
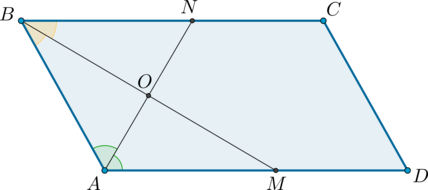
Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), тогда (angle DAB + angle ABC =
180^{circ}).
Так как (AN) и (BM) – биссектрисы, то (angle BAN + angle ABM =
0,5(angle DAB + angle ABC) = 0,5cdot 180^circ = 90^{circ}), откуда (angle AOB = 180^circ – (angle BAN + angle ABM) =
90^circ).
3. Пусть (AN) и (CM) – биссектрисы углов параллелограмма (ABCD).

Так как в параллелограмме противоположные углы равны, то (angle 2 =
0,5cdotangle BAD = 0,5cdotangle BCD = angle 1). Кроме того, углы (1) и (3) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (CM), тогда (angle 2 = angle 3), откуда следует, что (ANparallel CM). Кроме того, (AMparallel CN), тогда (ANCM) – параллелограмм, следовательно, (AN = CM).
Источник
Определение
Параллелограммом называется четырехугольник, у которого противоположные стороны попарно параллельны.
Точку пересечения диагоналей параллелограмма называют его центром.
Свойства параллелограмма:
Сумма любых двух соседних углов параллелограмма равна $180^{circ}$, а противоположные углы равны.
Противолежащие стороны параллелограмма равны.
Диагонали параллелограмма пересекаются и делятся точкой пересечения пополам.
Пусть дан параллелограмм $ABCD$.
1. Заметим, что соседние углы $A$ и $B$ параллелограмма являются внутренними односторонними при параллельных прямых $AD$ и $BC$ и секущей $AB$, то есть их сумма равна $180^circ$. Аналогично для других пар углов.
Если $angle A + angle B=180^circ$ и $angle C + angle B=180^circ$, то $angle A = angle C$. Аналогично, $angle B = angle D$.
2. Рассмотрим треугольники $ABC$ и $CDA$. Из параллельности противоположных сторон параллелограмма следует, что $angle BAC=angle DCA$ и $angle BCA=angle DAC$. Поскольку $AC$ — общая, то треугольники $ABC$ и $CDA$ равны по второму признаку. Из равенства треугольников следует, что $AB=CD$ и $BC=AD$.

3. Поскольку параллелограмм — выпуклый четырехугольник, то его диагонали пересекаются. Пусть $O$ — точка пересечения. Из параллельности сторон $BC$ и $AD$ параллелограмма следует, что $angle OAD=angle OCB$ и $angle ODA=angle OBC$. Учитывая равенство $BC=AD$ получим, что треугольники $AOD$ и $COB$ равны по второму признаку. Следовательно, $AO=CO$ и $DO=BO$, что и требовалось.

Признаки параллелограмма:
Если в четырехугольнике сумма любых двух соседних углов равна $180^{circ}$, то этот четырехугольник — параллелограмм.
Если в четырехугольнике противолежащие углы попарно равны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике противолежащие стороны попарно равны, то этот четырехугольник — параллелограмм.
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник — параллелограмм.
Если диагонали четырехугольника делятся точкой их пересечения пополам, то этот четырехугольник — параллелограмм.
Пусть дан четырехугольник $ABCD$.
1. Заметим, что соседние углы $A$ и $B$ являются внутренними односторонними при прямых $AD$ и $BC$ и секущей $AB$. Так как их сумма равна $180^circ$, то прямые $AD$ и $BC$ параллельны. Аналогично для другой пары прямых, то есть $ABCD$ — параллелограмм по определению.
2. Заметим, что $angle A + angle B + angle C + angle D=360^circ$. Если $angle A = angle C$, а $angle B = angle D$, то $angle A + angle B=180^circ$ и аналогично для других пар соседних углов. Далее используем предыдущий признак.
3. Рассмотрим треугольники $ABC$ и $CDA$. Поскольку $AC$ — общая, то из равенства противоположных сторон параллелограмма следует, что треугольники $ABC$ и $CDA$ равны по третьему признаку. Следовательно, $angle BAC=angle DCA$ и $angle BCA=angle DAC$, откуда следует параллельность противолежащих сторон.
4. Пусть $BC$ и $AD$ равны и параллельны. Рассмотрим треугольники $ABC$ и $CDA$. Из параллельности прямых следует, что $angle BCA=angle DAC$. Поскольку $AC$ — общая и $BC=AD$, то треугольники $ABC$ и $CDA$ равны по первому признаку. Следовательно, $AB=CD$. Далее используем предыдущий признак.
5. Пусть $O$ — точка пересечения диагоналей и $AO=CO$, а $DO=BO$.Учитывая равенство вертикальных углов, получим, что треугольники $AOD$ и $COB$ равны по первому признаку. Следовательно, $angle OAD=angle OCB$, откуда следует параллельность $BC$ и $AD$. Аналогично для другой пары сторон.
Определение
Четырехугольник, в котором есть три прямых угла, называется прямоугольником.
Свойства прямоугольника:
Диагонали прямоугольника равны.
Пусть дан прямоугольник $ABCD$. Поскольку прямоугольник является параллелограммом, то его противолежащие стороны равны. Тогда прямоугольные треугольники $ABD$ и $DCA$ равны по двум катетам, откуда следует, что $BD=AC$.
Признаки прямоугольника:
Если в параллелограмме есть прямой угол, то этот параллелограмм является прямоугольником.
Если диагонали параллелограмма равны, то этот параллелограмм является прямоугольником.
1. Если один из углов параллелограмма прямой, то, учитывая, что сумма соседних углов равна $180^{circ}$, получим, что прямыми являются и остальные углы.
2. Пусть в параллелограмме $ABCD$ диагонали $AC$ и $BD$ равны. Учитывая равенство противолежащих сторон $AB$ и $DC$, получим, что треугольники $ABD$ и $DCA$ равны по третьему признаку. Следовательно, $angle BAD=angle CDA$, то есть они прямые. Осталось воспользоваться предыдущим признаком.
Определение
Четырехугольник, в котором все стороны равны, называется ромбом.
Свойства ромба:
Диагонали ромба взаимно перпендикулярны и являются биссектрисами его углов.
Пусть в ромбе $ABCD$ диагонали $AC$ и $BD$ пересекаются в точке $O$. Так как ромб является параллелограммом, то $AO=OC$. Рассмотрим равнобедренный треугольник $ABC$. Так как $AO$ — медиана проведнная к основанию, то она является биссектрисой и высотой, что и требовалось.
Признаки ромба:
Если диагонали параллелограмма взаимно перпендикулярны, то этот параллелограмм является ромбом.
Если диагональ параллелограмма является биссектрисой его угла, то этот параллелограмм является ромбом.
Пусть в параллелограмме $ABCD$ диагонали $AC$ и $BD$ пересекаются в точке $O$. Рассмотрим треугольник $ABC$.
1. Если диагонали перпендикулярны, то $BO$ является в треугольнике медианой и высотой.
2. Если диагональ $BD$ содержит биссектрису угла $ABC$, то $BO$ является в треугольнике медианой и биссектрисой.
В обоих случаях получим, что треугольник $ABC$ — равнобедренный и в параллелограмме соседние стороны равны. Следовательно, он является ромбом, что и требовалось.
Определение
Прямоугольник, у которого две соседние стороны равны, называется квадратом.
Признаки квадрата:
Если у ромба есть прямой угол, то этот ромб является квадратом.
Если у ромба диагонали равны, то этот ромб является квадратом.
Если у параллелограмма есть прямой угол или равны диагонали, то он является прямоугольником. Если же четырехугольник является прямоугольником и ромбом, то он — квадрат.
Источник
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания (a) на высоту (h). Также можно найте его площадь через две стороны и угол и через диагонали.
Свойства параллелограмма
1. Противоположные стороны тождественны
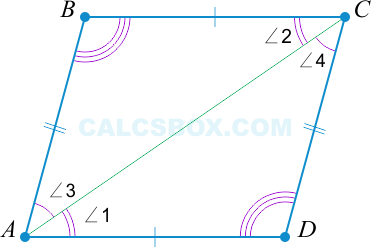
Первым делом проведем диагональ ( AC ). Получаются два треугольника: ( ABC ) и ( ADC ).
Так как ( ABCD ) — параллелограмм, то справедливо следующее:
( AD || BC Rightarrow angle 1 = angle 2 ) как лежащие накрест.
( AB || CD Rightarrow angle3 = angle 4 ) как лежащие накрест.
Следовательно, ( triangle ABC = triangle ADC ) (по второму признаку: ( angle 1 = angle 2, angle 3 = angle 4 ) и ( AC ) — общая).
И, значит, ( triangle ABC = triangle ADC ), то ( AB = CD ) и ( AD = BC ).
2. Противоположные углы тождественны
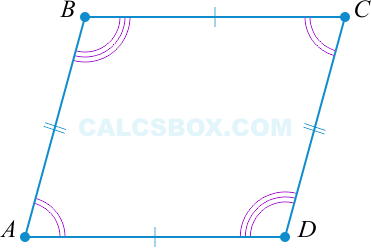
Согласно доказательству свойства 1 мы знаем, что ( angle 1 = angle 2, angle 3 = angle 4 ). Таким образом сумма противоположных углов равна: ( angle 1 + angle 3 = angle 2 + angle 4 ). Учитывая, что ( triangle ABC = triangle ADC ) получаем ( angle A = angle C ), ( angle B = angle D ).
3. Диагонали разделены пополам точкой пересечения
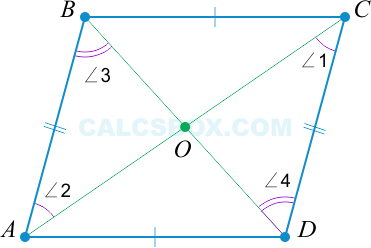
По свойству 1 мы знаем, что противоположные стороны тождественны: ( AB = CD ). Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что ( triangle AOB = triangle COD ) по второму признаку равенства треугольников (два угла и сторона между ними). То есть, ( BO = OD ) (напротив углов ( angle 2 ) и ( angle 1 )) и ( AO = OC ) (напротив углов ( angle 3 ) и ( angle 4 ) соответственно).
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны
( AB = CD ); ( AB || CD Rightarrow ABCD ) — параллелограмм.
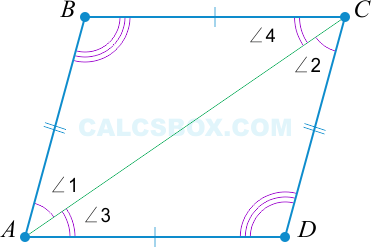
Рассмотрим подробнее. Почему ( AD || BC )?
( triangle ABC = triangle ADC ) по свойству 1: ( AB = CD ), ( angle 1 = angle 2 ) как накрест лежащие при параллельных ( AB ) и ( CD ) и секущей ( AC ).
Но если ( triangle ABC = triangle ADC ), то ( angle 3 = angle 4 ) (лежат напротив ( AD || BC ) (( angle 3 ) и ( angle 4 ) – накрест лежащие тоже равны).
Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны
( AB = CD ), ( AD = BC Rightarrow ABCD ) — параллелограмм.
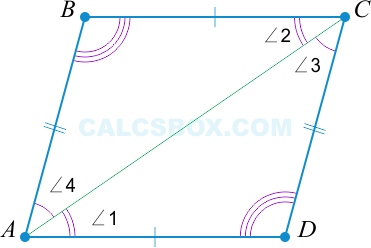
Рассмотрим данный признак. Еще раз проведем диагональ ( AC ).
По свойству 1 ( triangle ABC = triangle ACD ).
Из этого следует, что: ( angle 1 = angle 2 Rightarrow AD || BC ) и ( angle 3 = angle 4 Rightarrow AB || CD ), то есть ( ABCD ) — параллелограмм.
Второй признак верен.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны
( angle A = angle C ), ( angle B = angle D Rightarrow ABCD ) — параллелограмм.
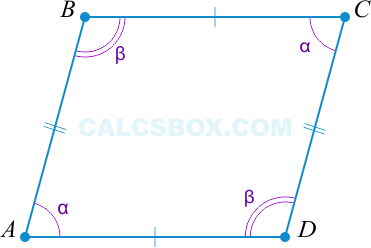
( 2 alpha + 2 beta = 360^{circ} ) (поскольку ( angle A = angle C ), ( angle B = angle D ) по условию).
Получается, ( alpha + beta = 180^{circ} ). Но ( alpha ) и ( beta ) являются внутренними односторонними при секущей ( AB ).
И то, что ( alpha + beta = 180^{circ} ) говорит и о том, что ( AD || BC ).
При этом ( alpha ) и ( beta ) — внутренние односторонние при секущей ( AB || CD ).
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам
( AO = OC ); ( BO = OD Rightarrow ) параллелограмм.
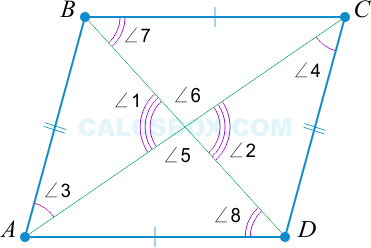
( BO = OD ); ( AO = OC ), ( angle 1 = angle 2 ) как вертикальные ( Rightarrow triangle AOB = triangle COD ), ( Rightarrow angle 3 = angle 4 ), и ( Rightarrow AB || CD ).
Аналогично ( BO = OD ); ( AO = OC ), ( angle 5 = angle 6 Rightarrow triangle AOD = triangle BOC Rightarrow angle 7 = angle 8 ), и ( Rightarrow AD || BC ).
Четвертый признак верен.
Источник
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Источник
Свойства параллелограмма
1. Противоположные стороны тождественны.

Доказательство
Первым делом проведем диагональ AC. Получаются два треугольника: ABC и ADC.

Так как ABCD — параллелограмм, то справедливо следующее:
AD || BC Rightarrow angle 1 = angle 2 как лежащие накрест.
AB || CD Rightarrow angle3 = angle 4 как лежащие накрест.
Следовательно, triangle ABC = triangle ADC (по второму признаку: angle 1 = angle 2, angle 3 = angle 4 и AC — общая).
И, значит, triangle ABC = triangle ADC, то AB = CD и AD = BC.
Доказано!
2. Противоположные углы тождественны.

Доказательство
Согласно доказательству свойства 1 мы знаем, что angle 1 = angle 2, angle 3 = angle 4. Таким образом сумма противоположных углов равна: angle 1 + angle 3 = angle 2 + angle 4. Учитывая, что triangle ABC = triangle ADC получаем angle A = angle C, angle B = angle D.
Доказано!
3. Диагонали разделены пополам точкой пересечения.

Доказательство
Проведем еще одну диагональ.

По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD. Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что triangle AOB = triangle COD по второму признаку равенства треугольников (два угла и сторона между ними). То есть, BO = OD (напротив углов angle 2 и angle 1) и AO = OC (напротив углов angle 3 и angle 4 соответственно).

Доказано!
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.

AB = CD; AB || CD Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим подробнее. Почему AD || BC?

triangle ABC = triangle ADC по свойству 1: AB = CD, AC — общая и angle 1 = angle 2 как накрест лежащие при параллельных AB и CD и секущей AC.
Но если triangle ABC = triangle ADC, то angle 3 = angle 4 (лежат напротив AB и CD соответственно). И следовательно AD || BC (angle 3 и angle 4 – накрест лежащие тоже равны).

Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны.

AB = CD, AD = BC Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим данный признак. Еще раз проведем диагональ AC.

По свойству 1 triangle ABC = triangle ACD.

Из этого следует, что: angle 1 = angle 2 Rightarrow AD || BC и angle 3 = angle 4 Rightarrow AB || CD, то есть ABCD — параллелограмм.
Второй признак верен.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны.

angle A = angle C, angle B = angle D Rightarrow ABCD — параллелограмм.
Доказательство

2 alpha + 2 beta = 360^{circ} (поскольку ABCD — четырехугольник, а angle A = angle C, angle B = angle D по условию).
Получается, alpha + beta = 180^{circ}. Но alpha и beta являются внутренними односторонними при секущей AB.
И то, что alpha + beta = 180^{circ} говорит и о том, что AD || BC.
При этом alpha и beta — внутренние односторонние при секущей AD. И это значит AB || CD.
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам.

AO = OC; BO = OD Rightarrow параллелограмм.
Доказательство

BO = OD; AO = OC, angle 1 = angle 2 как вертикальные Rightarrow triangle AOB = triangle COD, Rightarrow angle 3 = angle 4, и Rightarrow AB || CD.
Аналогично BO = OD; AO = OC, angle 5 = angle 6 Rightarrow triangle AOD = triangle BOC Rightarrow angle 7 = angle 8, и Rightarrow AD || BC.
Четвертый признак верен.
Источник
