Какими свойствами обладает параллельный перенос
Гипермаркет знаний>>Математика>>Математика 8 класс>>Математика: Параллельный перенос и его свойства
Параллельный перенос и его свойства
Общие сведения о параллельном переносе
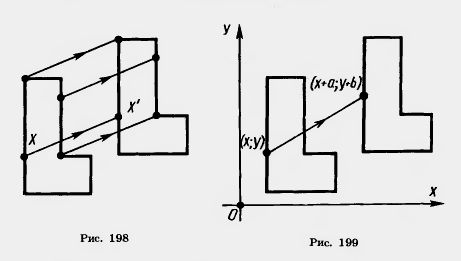
Наглядно параллельный перенос определяется как преобразование, при котором точки смещаются в одном и том же направлении на одно и то же расстояние (рис. 198). Такое определение не является математически строгим, потому что в нем употребляется выражение «в одном и том же направлении», которое само нуждается в точном определении. В связи с этим параллельному переносу мы дадим другое, отвечающее тому же наглядному представлению, но уже строгое определение.
Введем на плоскости декартовы координаты х, у. Преобразование фигуры F, при котором произвольная ее точка (х; у) переходит в точку (х + а; у + b), где а и b одни и те же для всех точек (х; у), называется параллельным переносом (рис. 199). Параллельный перенос задается формулами x’ = x + а, у’ = у + b.
Эти формулы выражают координаты х’, у’ точки, в которую переходит точка (х; у) при параллельном переносе.
Свойства параллельного переноса
Параллельный перенос есть движение.
Действительно, две произвольные точки А(х1; у1) к В (х2; у2) переходят при параллельном переносе в точки А’ (х1 +а; у1 + b), В'(х2 + а; y2+b). Поэтому
АВ2=(х2-х1)2+ (у2-у1 )2
A’B”2=(х2-х1)2+ (у2-у1 )2
Отсюда АВ=А’В’. Таким образом, параллельный перенос сохраняет расстояния, а значит, является движением, что и требовалось доказать.
Название «параллельный перенос» оправдывается тем, что при параллельном переносе точки смещаются по параллельным (или совпадающим) прямым на одно и то же расстояние.

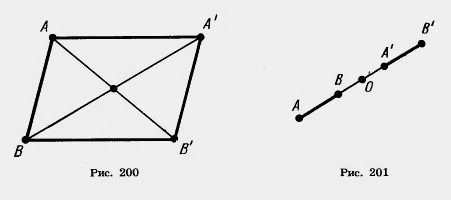
Действительно, пусть точки A (x1; y1) и В (x2; y2) переходят в точки A'(x1+а; y1 + b) и В’ (х2 + а; y2 + b) (рис. 200). Середина отрезка АВ’ имеет координаты
Те же координаты имеет и середина отрезка А’В. Отсюда следует, что диагонали четырехугольника АА’В’В пересекаются и точкой пересечения делятся пополам. Значит, этот четырехугольник — параллелограмм. А у параллелограмма противолежащие стороны А А’ и ВВ’ параллельны и равны.
Заметим, что у параллелограмма АА’В’В параллельны и две другие противолежащие стороны — АВ и А ‘В’. Отсюда следует, что при параллельном, переносе прямая переходит в параллельную прямую (или в себя).
Замечание. В предыдущем доказательстве предполагалось, что точка В не лежит на прямой АА’. В случае, когда точка В лежит на прямой АА’, точка В’ тоже лежит на этой прямой, так как середина отрезка АВ’ совпадает с серединой отрезка ВА’ (рис. 201). Значит, все точки А, В, А’, В’ лежат на одной прямой. Далее,
Таким образом, в этом случае точки АиВ смещаются по прямой АВ на одно и то же расстояние а прямая АВ переходит в себя.
Повторение темы о параллельном переносе
Мы с вами уже познакомились с такой темой, как параллельный перенос. На этом уроке вы узнали, что такое преобразование на плоскости, где все точки перемещаются на одно и то же расстояние, считается параллельным переносом.
Из данного урока, каждому из вас стало понятно, что параллельный перенос является движением, так как при таком переносе любая прямая переходит в такую же параллельную ей прямую.
Если мы посмотрим на рисунок, то можем наглядно представить такое движение, как сдвиг площади в направлении данного вектора на его длину.
Свойства, которыми обладает параллельный перенос в пространстве
• Во-первых, параллельный перенос является движением;
• Во-вторых, при выполнении этого действия все точки смещаются по параллельным прямым и притом на одно и то же расстояние;
• В-третьих, при таком переносе прямая имеет свойство переходить в такую же параллельную прямую или в себя саму;
• В-четвертых, независимо от того, какими точками были A и A’, но точка A переходит в точку A’.
• В-пятых, при таком переносе, т.е параллельном переносе в пространстве, в любом случае плоскость имеет свойство переходить в себя саму или же такую же параллельную ей плоскость.
Истрия и применение в науке
Как правило, в каждого понятия есть свой первооткрыватель, но автор параллельного переноса в пространстве, на жаль, нам неизвестен. А вот применение параллельного переноса в пространстве довольно широко. Как правило, такой перенос используют при преобразовании графической функции в математике, в механике, а также в кристаллографии.

Но если рассматривать трансляция или кристаллографию, то в этом случае перенос приобретает симметричное преобразование, в котором узел пространственной решётки должен совпасть с идентичным ближайшим узлом. В принципе, трансляцию можно отнести к частному случаю параллельного переноса, так как при сдвиге на определенный вектор ее свойства в данной системе не изменяются, а являются вектором трансляции и для нее свойственна трансляционная симметрия.
Примеры из жизни
В повседневной жизни мы с вами также постоянно сталкиваемся с примерами параллельного переноса в пространстве. Таким наглядным примером может быть, применяемая в строительной индустрии скользящая опалубка, этот процесс мы можем наблюдать и при перестановке мебели в квартире, да и следы от подошвы нам также напоминают о параллельном переносе в пространстве.
А также, параллельный перенос можно встретить и в таких необычных ситуациях:

А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний – Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.
Разработка – Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email:
По вопросам рекламы и спонсорства пишите на email:
Источник
В данной статье мы будем рассматривать понятие параллельного переноса в трехмерном пространстве. Но вначале нам надо рассмотреть такие понятия как отображение и движение в пространстве.
Понятие движения
Перед тем, как ввести понятие движения в пространстве, надо ввести определение отображения пространства на себя.
Определение 1
Отображением пространства на себя будем называть такое соответствие любой точке данного пространства какой-либо точке этого же пространства, в котором участвуют все точки из этого пространства.
Введем теперь, непосредственно, определение движения.
Определение 2
Движением пространства будем называть отображением пространства на себя, которое сохраняется расстояния между соответствующими точками.
Пример – рисунок 1.
Введем теперь несколько теорем, связанных с понятием движения без доказательства.
Теорема 1
При движении отрезок будет отображаться на ему же равный отрезок.
Теорема 2
При движении треугольник будет отображаться на равный ему же треугольник.
Теорема 3
При движении пирамида будет отображаться на равную ей пирамиду.
Основными примерами движений в геометрии являются осевая симметрия, центральная симметрия, зеркальная симметрия, поворот и параллельный перенос. Доказательство того, что параллельный перенос действительно является движением, нами будет рассмотрено ниже.
Параллельный перенос
Введем теперь, непосредственно, понятие параллельного переноса на какой-либо вектор. Пусть нам дан вектор $overline{α}$.
Определение 3
Параллельным переносом на вектор $overline{α}$ будем называть такое отображение плоскости само на себя, при котором произвольная точка $M$ отображается на такую точку $M_1$, что выполняется равенство $overline{MM_1}=overline{α}$
(Рис. 2).
Введем следующую теорему, связанную с понятием параллельного переноса.
Теорема 4
Параллельный перенос – движение.
Доказательство.
Рассмотрим в пространстве две произвольные точки $M$ и $N$. Будем рассматривать параллельный перенос на данный нам вектор $overline{α}$. Пусть при нашем параллельном переносе данные нам точки отображаются, соответственно, в точки $M_1$ и $N_1$ (рис. 3).
Из определения 3 параллельного переноса получим, что $overline{MM_1}=overline{a}$, а $overline{NN_1 }=overline{a}$, следовательно, получим, что $overline{MM_1}=overline{NN_1}$.
Тогда, из определения равных векторов будем получать, что
$|MM_1|=|NN_1|$, $MM_1||NN_1$
Получаем, что четырехугольник $MM_1N_1N$ будет являться параллелограммом и, как следствие, верно равенство: $|MN|=|M_1N_1|$. Отсюда получаем, что параллельный перенос будет сохранять расстояния, что и доказывает нашу теорему.
Пример задачи
Пример 1
Постройте параллельный перенос куба на вектор $overline{h}$, изображенных на рисунке 4.
Решение.
Для построения параллельного переноса сначала проведем через все точки тетраэдра прямые, параллельные заданному нам вектору $overline{h}$ (рис. 5).
Далее, для построения будем использовать определение 3. Точка $X$ перейдет в такую точку $X_1$, которая будет принадлежать прямой $x$. Точка $Y$ перейдет в такую точку $Y_1$, которая будет принадлежать прямой $y$. Точка $Z$ перейдет в такую точку $Z_1$, которая будет принадлежать прямой $z$. Точка $O$ перейдет в такую точку $O_1$, которая будет принадлежать прямой $o$. Точка $X’$ перейдет в такую точку $X’_1$, которая будет принадлежать прямой $a$. Точка $Y’$ перейдет в такую точку $Y’_1$, которая будет принадлежать прямой $b$. Точка $Z’$ перейдет в такую точку $Z’_1$, которая будет принадлежать прямой $c$. Точка $O’$ перейдет в такую точку $O’_1$, которая будет принадлежать прямой $o’$. Причем будут выполняться равенства:
$overline{XX_1}=overline{h}$, $overline{YY_1}=overline{h}$, $overline{ZZ_1}=overline{h}$, $overline{OO_1}=overline{h}$, $overline{X’X’_1}=overline{h}$, $overline{Y’Y’_1}=overline{h}$, $overline{Z’Z’_1}=overline{h}$, $overline{O’O’_1}=overline{h}$
Отметим эти точки (рис. 6).
Соединив эти точки между собой, мы и получим искомый нами параллельный перенос на вектор $overline{h}$ (рис. 7).
Источник
Параллельный перенос, симметрия относительно плоскости.
Цель:
Сформировать понятие параллельного переноса;
Рассмотреть симметрию относительно плоскости.
Параллельный перенос
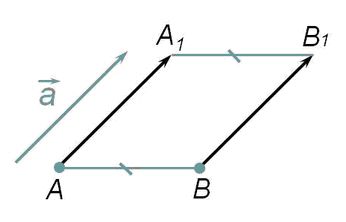
Параллельным переносом фигуры называется перенос всех точек пространства на одно расстояние в одном направлении.
Параллельный перенос определяет вектор, по которому совершается перенос.
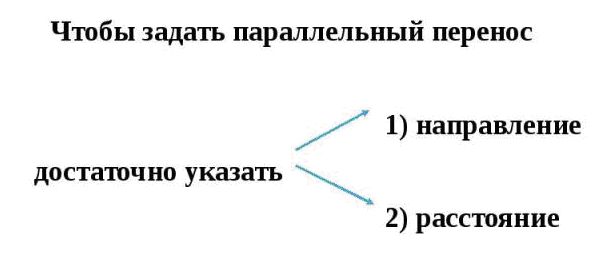
Чтобы совершить параллельный перенос, нужно знать направление и расстояние, что означает задать вектор.

Чтобы при параллельном переносе построить изображение многоугольника, достаточно построить изображения вершин этого многоугольника.
Первоначальная фигура и фигура, полученная после параллельного переноса, равны.
Параллельный перенос используется для конструирования графиков функций.
На рисунке изображена парабола и два результата параллельного переноса.

Иногда параллельный перенос встречается в необычных ситуациях:

Симметрия
Термин «cимме́три́я» — (др.-греч. συμμετρία) по гречески означает «соразмерность, пропорциональность, одинаковость в расположении частей»
Математически строгое представление о симметрии сформировалось сравнительно недавно – в XIX веке. В наиболее простой трактовке известного немецкого математика Германа Вейля (1855-1955) современное определение симметрии выглядит так: симметричным называется такой объект, который можно как-то изменять, получая в результате то же, с чего начали.
Мы будем называть симметрией фигуры любое преобразование, переводящее фигуру в себя, т.е. обеспечивающее ее самосовмещение.
Перечислим виды симметрии.
Виды симметрии
Осевая симметрия
Преобразование, при котором каждая точка A фигуры (или тела) преобразуется в симметричную ей относительно некоторой оси l точу А, при этом отрезок AA´ l , называется осевой симметрией.

Если точка А лежит на оси l, то она симметрична самой себе, т.е. A совпадает с A´.
В частности, если при преобразовании симметрии относительно оси l,
фигура F переходит сама в себя, то она называется симметричной относительно оси l, а ось l называется ее осью симметрии.

Центральная симметрия.
Преобразования, переводящее каждую точку A фигуры или тела в точку A´, симметричную ей относительно центра O, называетсяпреобразованием центральной симметрии или просто центральной симметрией.

Точка O называется центром симметрии и является неподвижной. Других неподвижных точек это преобразование не имеет. Если при преобразовании центральной симметрии относительно центра О фигура F преобразуется в себя, то она называется симметричной относительно центра O.при этом центр O называется центром симметрии фигуры F. Примерами фигур, обладающих центром симметрии, являются параллелограмм, окружность и т.д.

Знакомые понятия поворота и параллельного переноса используются при определении так называемой трансляционной симметрии.
Рассмотрим трансляционную симметрию более подробно.
Трансляционная симметрия
Поворот
Преобразование, при котором каждая точка A фигуры или тела поворачивается на один и тот же угол α вокруг заданного центра O, называется вращением или поворотом плоскости. Точка О называется центром вращения, а угол α – углом вращения. Точка O является неподвижной точкой этого преобразования.

Центральная симметрия есть поворот фигуры или тела на 180˚.
Параллельный перенос.
Преобразование при котором каждая точка фигуры или тела перемещается в одном и том же направлении на одно и то же расстояние, называется параллельным переносом.
Чтобы задать преобразование параллельного переноса, достаточно задать вектор .

Скользящая симметрия
Скользящей симметрией называется такое преобразование, при котором последовательно выполняются осевая симметрия и параллельный перенос.

Все перечисленные преобразования будем называть преобразованиями симметрии. Для преобразований симметрии имеют место следующие свойства:
отрезок переходит в равный ему отрезок;
угол переходит в равный ему угол;
окружность переходит в равную ей окружность;
любой многоугольник переходит в равный ему многоугольник и т.д.
параллельные прямые переходят в параллельные, перпендикулярные в перпендикулярные.
* В стереометрии вводится еще один вид симметрии –
Источник
Определение. Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (х,у,г) фигуры переходит в точку (х+ a;y + b;z + c), где а, Ъ, с—постоянные.
Параллельный перенос в пространстве задается формулами
х” = х + а, у’ = у + b, z” = z+ с,
выражающими координаты (х”, у’, z1) точки, в которую переходит точка (х,у, z) при параллельном переносе. Так же, как на плоскости, доказываются следующие свойства параллельного переноса.
1. Параллельный перенос есть движение.
2.При параллельном переносе точки смещаются по парал
лельным (или совпадающим) прямым на одно и то же расстояние.
3.При параллельном переносе каждая прямая переходит в
параллельную ей прямую (или в себя).
4.Каковы бы ни были точки ХиХ, существует единственный
параллельный перенос, при котором точка X переходит в точку X”.
В пространстве добавляется еще одно свойство параллельного переноса.
5.При параллельном переносе в пространстве каждая плоскость
переходит либо в себя, либо в параллельную ей плоскость.
Докажем последнее свойство.
Пусть а — произвольная плоскость (рис. 54). Проведем в этой плоскости две пересекающиеся прямые а и ft. При параллельном переносе прямые а и Ъ переходят либо в себя, либо в параллельные прямые а1и Ь1. Плоскость а переходит в некоторую плоскость а1, проходящую через прямые а1 и б1. Если плоскость а1 не совпадает с а, то по теореме 8 она параллельна а. Что и требовалось доказать.
Вопросыи задания
1.Сколько координат имеет точка в пространстве?
2. Как найти координаты точки в пространстве?
3. Запишите формулу расстояния между двумя точками через координаты этих
точек. Имеет ли значение порядок точек и их координат?
4. Какими формулами определяются координаты середины отрезка?
15. Дайте определение параллельного переноса.
16. Перечислите свойства параллельного переноса.
Задачи
173.Даны точки А(1; 7; 4), В(3; 0; 0), С(1; 2; 0), Щ); 5; 1). Какие из этих
точек лежат: 1) в плоскости ху; 2) в плоскости у г; 3) на оси х?
174.Дана точка М(2; 4; 6). Найдите основания перпендикуляров,
опущенных из этой точки на координатные оси и координатные
плоскости.
175.Даны вершины А(1; -3; 0), В(-2; -4; 1), С(-3; 1; 1), Щ); 2; 0)
параллелограмма ABCD. Вычислите длины диагоналей паралле
лограмма.
176.Найдите расстояния от точки (2; -2; 3) до: 1) координатных
плоскостей; 2) осей координат; 3) начала координат.
177.Какая из точек: А(2; 1; 5) или В(–2; 1; 6) — лежит ближе к началу
координат?
178.При параллельном переносе точка А(3; 2; -1) переходит в точку
А2; 0; -1). В какую точку переходит начало координат?
В
179.Даны точки М (0; 1; 1), JV(2; -1; 3), 2sT(-l; у, 0). Найдите такое
значение у, чтобы выполнялось условие: МЩ = NK].
180.Найдите координаты точки, лежащей на оси у и равноудаленной
от точек Р( 4; -1; 3) и Q(l; 3; 0).
181.Найдите координаты точки, лежащей в плоскости ху и равно
удаленной от точек А(0; 1; 0), В(-1; 0; 1), С(0; -1; 0).
182.Докажите, что четырехугольник ABCD является ромбом, если:
А(0; 2; 0), ВЦ; 0; 0), С(2; 0; 2), Щ1; 2; 2).
183.Найдите координаты вершины D параллелограмма ABCD, если
координаты трех других его вершин известны:
А(4; 2; -1), Б(1; -3; 2), С(-4; 2; 1).
184. Существует ли параллельный перенос, при котором точка А пере
ходит в точку В, а точка С — в точку D, если: А(0; 1; 2), .В(-1; 0; 1),
С(3; -2; 2), Щ2; -3; 1)?
Date: 2015-04-23; view: 2175; Нарушение авторских прав
Источник

Параллельный перенос и его свойства

Параллельный перенос Определение Доказательство Свойства
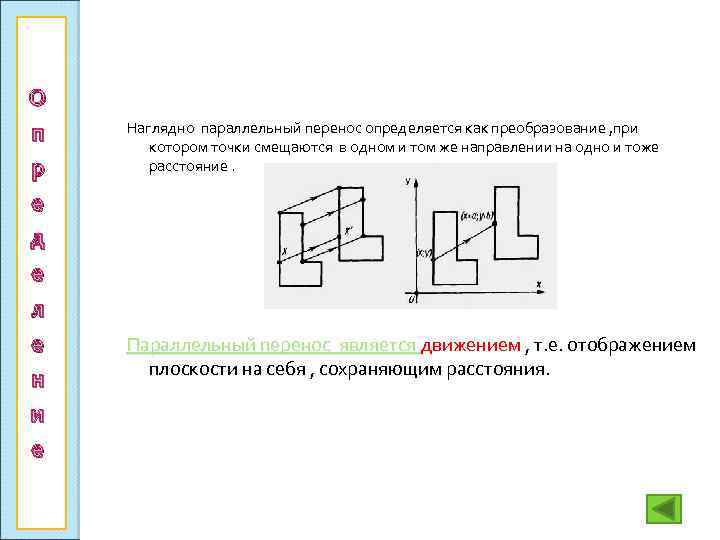
О п р е д е л е н и е Наглядно параллельный перенос определяется как преобразование , при котором точки смещаются в одном и том же направлении на одно и тоже расстояние. Параллельный перенос является движением , т. е. отображением плоскости на себя , сохраняющим расстояния.

(рис. 329) Пусть при параллельном переносе на вектор точки M и N отображаются в точки M 1 и N 1. Так как = , то =. Отсюда следует, что || и МM 1 = NN 1 , поэтому четырехугольник MM 1 N 1 N – параллелограмм. Следовательно, МN = M 1 N 1 , т. е. расстояние между точками М и N равно расстоянию между точками M 1 и N 1. Параллельный перенос является движением.
Свойства Параллельный перенос-движение При параллельном переносе прямая переходит в параллельную прямую, либо в себя.

Совокупность всех параллельный переносов образует группу, которая в евклидовом пространстве* является нормальной подгруппой группы движений, а в аффинном* ― нормальной подгруппой группы аффинных преобразований*. *Евклидово пространство — в изначальном смысле, пространство, свойства которого описываются аксиомами евклидовой геометрии. *Аффинное пространство — пространство, обобщающее аффинные свойства евклидова пространства. Во многом схоже с векторным пространством; однако для аффинного пространства, в отличие от векторного, характерно то, что все точки являются равноправными (в частности, в нём не определено понятие нулевой точки, или начала отсчёта). *Преобразование плоскости называется аффинным, если оно взаимно однозначно и образом любой прямой является прямая. Преобразование называется взаимно однозначным, если оно разные точки переводит в разные, и в каждую точку переходит какая-то точка.
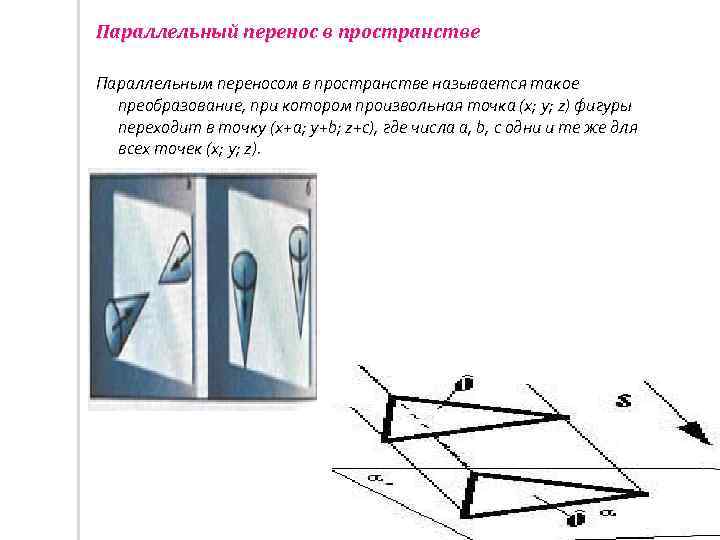
Параллельный перенос в пространстве Параллельным переносом в пространстве называется такое преобразование, при котором произвольная точка (x; y; z) фигуры переходит в точку (x+a; y+b; z+c), где числа a, b, с одни и те же для всех точек (x; y; z).
Параллельный перенос в пространстве обладает следующими свойствами: 1. Параллельный перенос есть движение. 2. При параллельном переносе точки смещаются по параллельным прямым на одно и то же расстояние. 3. При параллельном переносе каждая прямая переходит в параллельную ей прямую или в себя. 4. Каковы бы ни были точки A и A`, существует единственный параллельный перенос, при котором точка A переходит в точку A`. 5. При параллельном переносе в пространстве каждая плоскость переходит либо в себя, либо в параллельную ей плоскость.

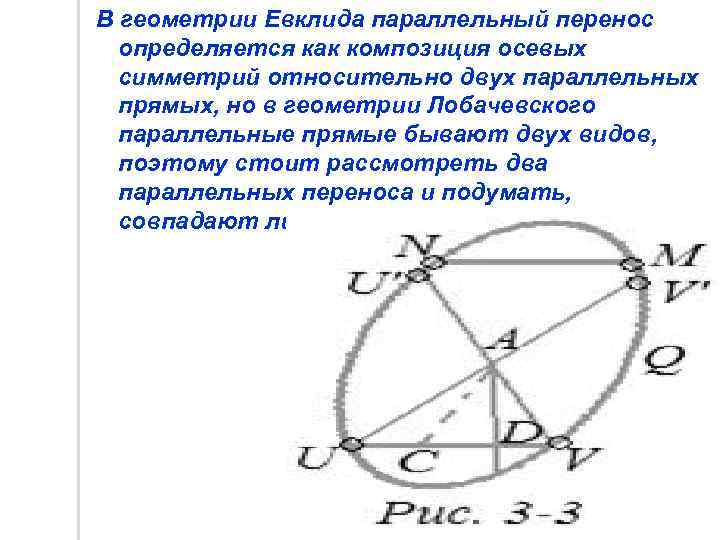
В геометрии Евклида параллельный перенос определяется как композиция осевых симметрий относительно двух параллельных прямых, но в геометрии Лобачевского параллельные прямые бывают двух видов, поэтому стоит рассмотреть два параллельных переноса и подумать, совпадают ли они.
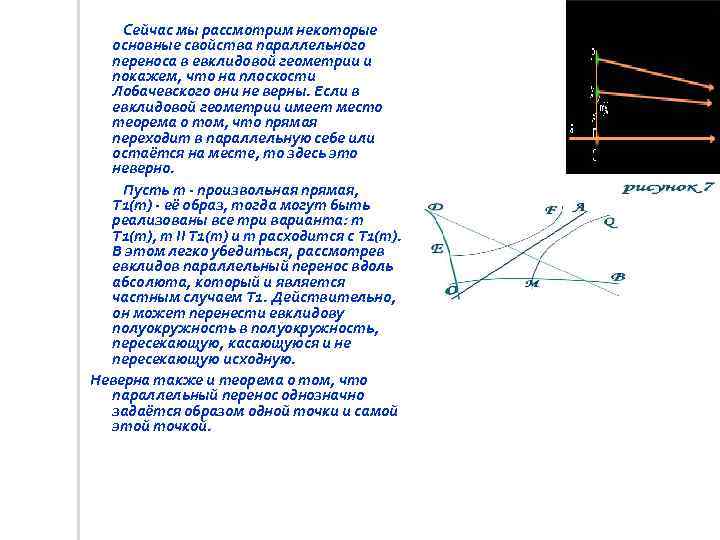
Сейчас мы рассмотрим некоторые основные свойства параллельного переноса в евклидовой геометрии и покажем, что на плоскости Лобачевского они не верны. Если в евклидовой геометрии имеет место теорема о том, что прямая переходит в параллельную себе или остаётся на месте, то здесь это неверно. Пусть m – произвольная прямая, Т 1(m) – её образ, тогда могут быть реализованы все три варианта: m Т 1(m), m II Т 1(m) и m расходится с Т 1(m). В этом легко убедиться, рассмотрев евклидов параллельный перенос вдоль абсолюта, который и является частным случаем Т 1. Действительно, он может перенести евклидову полуокружность в полуокружность, пересекающую, касающуюся и не пересекающую исходную. Неверна также и теорема о том, что параллельный перенос однозначно задаётся образом одной точки и самой этой точкой.
Источник
