Какими свойствами обладает нормальное распределение случайных погрешностей
Случайной
погрешностью измерения называется
составляющая погрешности, изменяющаяся
случайным образом (по знаку и значению)
при повторных измерениях одной и той
же физической величины, проведенных
с одинаковой тщательностью. Примеры
распределения случайных величин
Способы
нахождения значений случайной величины
зависят от вида функции ее распределения.
Однако на практике такие функции, как
правило, неизвестны. Если же случайный
характер результатов наблюдений
обусловлен погрешностями измерений,
то полагают, что наблюдения имеют
нормальное
распределение.
Это обусловлено тем, что погрешности
измерений складываются из большого
числа небольших возмущений, ни одно из
которых не является преобладающим.
Согласно же центральной
предельной теореме
сумма бесконечно большого числа взаимно
независимых бесконечно малых случайных
величин с любыми распределениями имеет
нормальное
распределение.
Нормальное распределение для
![]() случайной
случайной
величиных
с
математическим ожиданием
![]() и
и
дисперсиейs
имеет вид:
Реально даже воздействие
ограниченного числа возмущений приводит
к нормальному распределению результатов
измерений и их погрешностей. В
настоящее время наиболее полно разработан
математический аппарат именно для
случайных величин, имеющих нормальное
распределение. Если же предположение
о нормальности распределения отвергается,
то статистическая обработка наблюдений
существенно усложняется и в таком
случае невозможно рекомендовать общую
методику статистической обработки
наблюдений. Часто даже не известно,
какая характеристика распределения
может служить оценкой истинного значения
измеряемой величины.
Выше приведено
аналитическое выражение нормального
распределения для случайной измеряемой
величины х.
Переход к нормальному
распределению случайных погрешностей
![]() осуществляется
осуществляется
переносом центра распределений в![]() и
и
откладывания по оси абсцисс погрешности![]() .
.
Нормальное
распределение характеризуется двумя
парамет-рами: математическим ожиданием
m1
и
средним квадратическим отклонением
σ.
При многократных измерениях
несмещенной, состоятельной и эффективной
оценкой m1
для группы из n
наблюдений является среднее арифметическое
![]() :
:![]() .
.
Нужно
сказать, что среднее арифметическое
дает оценку математического ожидания
результата наблюдений и может бытьоценкой
истинного (действительного) значения
измеряемой
величины только после
исключения
систематических погрешностей.
Оценка
S
среднего квадратического отклонения
(СКО) дается
формулой:
![]() Эта
Эта
оценка характеризуетрассеяние
единичных результатов измерений в ряду
равноточных измерений одной и той же
величины около их среднего значения.
Другими оценками рассеяния результатов
в ряду измерений являются размах
(разница между наибольшим и наименьшим
значением), модуль средней
арифметической погрешности
(арифметическая сумма погрешностей,
деленная на число измерений) и
доверительная граница погрешности
(подробно рассматривается ниже).
СКО
является наиболее удобной характеристикой
погрешности в случае ее дальнейшего
преобразования. Например, для нескольких
некоррелированных слагаемых СКО суммы
определяется по
формуле:
![]() .
.
Оценка
S характеризует рассеяние единичных
результатов наблюдений относительно
среднего значения, то есть в случае,
если мы за результат измерений примем
отдельный исправленный результат
наблюдений. Если же в качестве результата
измерений принимается среднее
арифметическое, то СКО этого среднего![]() определяется
определяется
по формуле:![]() Нормальное
Нормальное
распределение погрешностей имеет
следующиесвойства:
симметричность,
т.е. погрешности, одинаковые по величине,
но противоположные по знаку,
встречаются одинаково часто;математическое
ожидание случайной погрешности равно
нулю;малые
погрешности более вероятны, чем большие;чем
меньше s, тем меньше рассеяние результатов
наблюдений и больше вероятность малых
погрешностей.
Доверительные
интервалы
Приведенные
выше оценки параметров распределения
случайных величин в виде среднего
арифметического для оценки математического
ожидания и СКО для оценки дисперсии
называются точечными
оценками,
так как они выражаются одним числом.
Однако в некоторых случаях знание
точечной оценки является недостаточным.
Наиболее корректной и наглядной оценкой
случайной погрешности измерений
является оценка с помощью доверительных
интервалов.
Симметричный интервал в границами
± Δх(Р)
называется доверительным
интервалом случайной
погрешности с довери-тельной вероятностью
Р,
если площадь кривой распределения
между абсциссами –Δх
и
+Δх
составляет Р-ю
часть всей площади под кривой плотности
распределения вероятностей. При
нормировке всей площади на единицу Р
представляет часть этой площади в долях
единицы (или в процентах). Другими
словами, в интервале от -Dх(Р)
до +Dх(Р)
с заданной вероятностью Р
встречаются Р×100%
всех возможных значений случайной
погрешности.
Доверительный интервал
для нормального распределения находится
по формуле:
![]() где
где
коэффициентt
зависит от доверительной вероятности
Р.
Для
нормального распределения существуют
следующие соотношения между доверительными
интервалами и доверительной вероятностью:
1s (Р=0,68), 2s (Р= 0,95), 3s (Р= 0,997), 4s (Р=0,999).
Доверительные
вероятности для выражения результатов
измерений и погрешностей в различных
областях науки и техники принимаются
равными. Так, в технических измерениях
принята доверительная вероятность
0,95. Лишь для особо точных и ответственных
измерений принимают более высокие
доверительные вероятности. В метрологии
используют, как правило, доверитель-ные
вероятности 0,97, в исключительных случаях
0,99. Необходимо отметить, что точность
измерений должна соответствовать
поставленной измерительной задаче.
Излишняя точность ведет к неоправданному
расходу средств. Недостаточная точность
измерений может привести к принятию
по его результатам ошибочных решений
с самыми непредсказуемыми последствиями,
вплоть до серьезных материальных потерь
или катастроф.
При
проведении многократных измерений
величины х,
подчиняющейся нормальному распределению,
доверительный интервал может быть
построен для любой доверительной
вероятности по формуле:
![]() гдеtq–
гдеtq–
коэффициент Стьюдента, зависящий от
числа наблюдений n
и выбранной доверительной вероятности
Р.
Он определяется с помощью таблицы
q-процентных
точек распределения Стьюдента, которая
имеет два параметра: k
= n
– 1 и q=
1 – P;
![]() –
–
оценка среднего квадратического
отклонения среднего арифметического.
Доверительный
интервал для погрешностиDх(Р)
позволяет построить доверительный
интервал для истинного (действительного)
значения измеряемой величины ,
оценкой которой является среднее
арифметическое
![]() .
.
Истинное значение измеряемой величины
находится с доверительной вероятностью
Р внутри интервала:![]() .
.
Доверительный интервал позволяет
выяснить, насколько может измениться
полученная в результате данной серии
измерений оценка измеряемой величины
при проведении повторной серии измерений
в тех же условиях. Необходимо отметить,
что доверительные интервалы строят
длянеслучайных
величин,
значения которых неизвестны. Такими
являются истинное значение измеряемой
величины и средние квадратические
отклонения. В то же время оценки этих
величин, получаемые в результате
обработки данных наблюдений, являются
случайными величинами.
Недостатком
доверительных интервалов при оценке
случай-ных погрешностей является то,
что при произвольно выбираемых
доверительных вероятностях нельзя
суммировать несколько погреш-ностей,
т.к. доверительный интервал суммы не
равен сумме довери-тельных интервалов.
Суммируются
дисперсии независимых случай-ных
величин:
Då
= åDi.
То есть, для возможности суммирования
составляющие случайной погрешности
должны быть представлены своими СКО,
а не предельными или доверительными
погрешностями.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Источник
Нормальный закон распределения получил широкое применение в практической метрологии, что объясняется центральной предельной теоремой теории вероятностей (теоремой Ляпунова), согласно которой распределение случайных погрешностей будет близко к нормальному во всех случаях, когда результаты наблюдений формируются под влиянием большого числа независимых факторов, каждый из которых оказывает незначительное действие по сравнению с суммарным действием остальных.
Нормальный закон распределения характеризуется свойствами:
– погрешность может принимать непрерывный ряд значений от до ;
– равные по абсолютному значению погрешности и равновероятны;
– малые по абсолютному значению погрешности более вероятны, чем большие.
Нормальный закон распределения описывается выражением
, (2.9)
где – среднеквадратическое отклонение погрешности .
График нормального закона распределения представлен на рисунке 2.1.
Рисунок 2.1 – График нормального закона распределения плотности
вероятности случайных погрешностей
Из графиков следует, что центр распределения находится в нуле, т.е. в точке нулевой погрешности . По мере удаления от центра распределения вероятность появления погрешности уменьшается. Чем больше , тем выше вероятность появления более точных результатов измерений, о чем говорит более высокий уровень максимума при большем .
В теории вероятностей часто используется понятие дисперсия D, характеризующая рассеяние погрешностей относительно центра распределения
. (2.10)
Дисперсия D связана с среднеквадратическим отклонением соотношением
. (2.11)
Для определения вероятности при нормальном законе распределения случайной погрешности необходимо вычислить интеграл
. (2.12)
Для симметричного интервала распределения погрешностей от до будем иметь
. (2.13)
Если в подинтегральном выражении вероятности заменить погрешность на относительную , получим нормированный нормальный закон распределения плотности вероятностей
. (2.14)
График нормированного нормального закона распределения соответствует нормальному закону распределения, приведенному на рисунке 2.1 при .
На практике часто используют интеграл вероятностей , который численно равен вероятности при интегрировании нормированного нормального закона распределения плотности вероятностей в пределах от нуля до z, где
. (2.15)
Значения интеграла вероятностей в зависимости от пределов интегрирования приведены в таблице 2.1. Пользуясь таблицей значений интеграла вероятностей можно выполнять вычисления интервала погрешности измерений по заданной вероятности или вероятности по заданным границам погрешности измерений.
Для оценки погрешности измерений используют среднеквадратическое отклонение , равновероятную () погрешность , максимальную () погрешность .
Таблица 2.1 – Значения интеграла вероятностей
Пользуясь таблицей значений интеграла вероятностей можно выполнять вычисления интервала погрешности измерений по заданной вероятности или вероятности по заданным границам погрешности измерений.
Нормальный закон распределения применяют для обработки результатов измерений при числе повторных измерений больше 20.
Источник
Группа случайных погрешностей измерения одной и той же величины подчиняется нормальному закону распределения Гаусса.
Не надо иронизировать в отношении такого названия – «нормальный закон распределения». Мол, если есть «нормальный закон», то должен быть и «ненормальный закон». Последних нет. Есть множество законов распределения, которые отличаются своими параметрами от нормального закона. Просто исследованиями установлено, что отклонения результатов измерений от истинного значения подчиняются в своей группе нормальному закону распределения Гаусса. И не только отклонения результатов измерений подчиняются этому закону, но и распределение самих результатов также, как говорят, нормальное.
Рассмотрим ряд случайных погрешностей, определяемых как отклонение результата измерения хi одной и той же величины, свободного от грубых и систематических погрешностей, от истинного значения Х:
. (3.3)
На основании теоретических иследований и опытных данных установлены следующие свойства ряда случайных погрешностей, подчиняющихся нормальному закону распределения, являющемуся симметричным.
Свойство 1. При многократном (бесконечно большом числе измерений) выполнении измерений одной величины равновероятно появление случайных погрешностей, равных по величине, но противоположных по знаку.
То есть, если была получена погрешность «- 0,085 м», то следует ожидать с той же вероятностью и погрешности «+ 0,085 м». Пусть даже это и произойдёт не тут же, но обязательно произойдёт в какое-то время.
Свойство 2. При большом числе измерений малые по абсолютной величине погрешности встречаются чаще, чем большие.
То есть, более всего ожидается результат измерений, близкий к истинному его значению.
Свойство 3. При неизменных условиях измерений случайные погрешности не превосходят по абсолютной величине известного предела:
. (3.4)
То есть, совокупность действия различных факторов, если условия измерений неизменны, не приведет к значительному уклонению результата измерений от его истинного значения.
С математической точки зрения это не совсем правильно, потому что нормальный закон распределения имеет бесконечные пределы в ту и другую стороны. То есть математики могут ожидать появление случайной погрешности, равной весьма большому числу, даже почти бесконечности. Пусть и вероятность этого почти равна нулю, но, всё же, не нулю. А с практической точки зрения целесообразно ввести ограничение на предельное значение случайной погрешности.
Если же это случится, т.е. появится результат, погрешность которого будет больше предельной, то следует считать это измерение содержащим грубую погрешность, исключить его из ряда измерений и заменить это измерение новым измерением.
Свойство 4. При большом числе измерений среднее арифметическое из случайных погрешностей стремится к нулю, т.е.
(при n → ∞ ). (3.5)
Здесь и в дальнейшем квадратные скобки […] являются символом суммы (символ введен Гауссом).
При большом числе измерений это вытекает из свойства 1 в силу симметрии нормального закона распределения (свойство компенсации).
Среднее арифметическое
В теории измерений и в практике обработки результатов измерений используются различные средние. Об одной из таких средних, средней арифметической, уже неоднократно упоминалось раньше. Часто используют в исследованиях среднее квадратическое, среднее геометрическое, среднее гармоническое и др. Нас, в данном случае, будет интересовать только среднее арифметическое.
Как уже говорилось выше, погрешность измерения представляет собой разность между самим результатом измерения хi и его истинным значением Х, определяемую по формуле (3.3).
Если результат измерения заранее известен, то, казалось бы, зачем производить измерения? Однако такие действия часто приходится выполнять. Например, при проверке правильности работы или показаний прибора по эталону. Да и при самих непосредственных измерениях, например, углов в треугольнике, сумма углов треугольника (или многоугольника) на плоскости является эталоном, известной величиной.
В основном результаты измерений заранее неизвестны. Что же представляет собой погрешность измерений в этом случае, и каким образом можно её определить?
Рассмотрим ряд измерений одной и той же величины Х для случая, когда число измерений весьма большое (n ® ∞). Составим ряд истинных погрешностей измерений, полагая, что измеряемая величина нам известна.
Сложим все разности в правых и левых частях формул (3.3) и разделим полученные результаты на n, получим
. (3.6)
В соответствии со свойствами случайных погрешностей отношение [D]/n стремится к нулю при n ® ∞ . Отношение [х]/n = хо называется средним арифметическим из результатов измерений.
С учетом сказанного можно записать, что
( ® Х) n ® ∞ , (3.7)
т.е. среднее арифметическое из результатов измерений при большом числе измерений стремится к истинному значению измеряемой величины. Это очень важное свойство многократных измерений, ряд которых подчиняется нормальному закону распределения.
Как просто! Чтобы получить истинное значение надо только выполнить большое число измерений, лучше всего – бесконечное их число. Но такой возможности, к сожалению, нет, поскольку большое число измерений (избыточных) приводит к большим затратам времени и большим экономическим затратам.
Таким образом, при определении погрешностей измерений с какой-то долей надёжности, зависящей от числа измерений, можно использовать величину среднего арифметического вместо истинного значения измеряемой величины. В этом случае истинные погрешности будут являться уклонениями результатов измерений от среднего арифметического:
vi = хi – xо . (3.8)
В теории погрешностей измерений доказано, что если результаты измерений подчиняются нормальному закону распределения, то и ряд уклонений vi от арифметического среднего также подчиняется нормальному закону распределения и обладает всеми свойствами случайных погрешностей.
Дата добавления: 2015-11-05; просмотров: 1570 | Нарушение авторских прав | Изречения для студентов
Читайте также:
Рекомендуемый контект:
Поиск на сайте:
© 2015-2020 lektsii.org – Контакты – Последнее добавление
Источник
Полным описанием случайной величины, а следовательно и погрешности, является ее закон распределения, которым определяется характер появления различных результатов отдельных измерений.
В практике электрических измерений встречаются различные законы распределения, некоторые из которых рассмотрены ниже.
Нормальный закон распределения (закон Гаусса). Этот закон является одним из наиболее распространенных законов распределения погрешностей. Объясняется это тем, что во многих случаях погрешность измерения образуется под действием большой совокупности различных, независимых друг от друга причин. На основании центральной предельной теоремы теории вероятностей результатом действия этих причин будет погрешность, распределенная по нормальному закону при условии, что ни одна из этих причин не является существенно преобладающей.
Нормальный закон распределения погрешностей описывается формулой
где ω(Δx) —плотность вероятности погрешности Δx; σ[Δx]— среднее квадратическое отклонение погрешности; Δxc — систематическая составляющая погрешности.
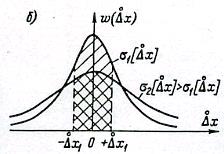
Вид нормального закона представлен на рис. 1,а для двух значений σ[Δx]. Так как
, то закон распределения случайной составляющей погрешности
имеет тот же вид (рис 1,б) и описывается выражением
где — среднее квадратическое отклонение случайной составляющей погрешности; = σ[Δx]
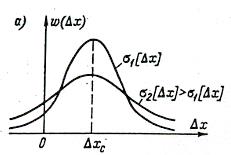

Рис. 1. Нормальный закон распредёления погрешности измерений (а) и случайной составляющей погрешности измерений (б)
Таким образом, закон распределения погрешности Δx отличается от закона распределения случайной составляющей погрешности только сдвигом по оси абсцисс на величину систематической составляющей погрешности Δхс.
Из теории вероятностей известно, что площадь под кривой плотности вероятности характеризует вероятность появления погрешности. Из рис.1, б видно, что вероятность Р появления погрешности в диапазоне ± при больше, чем при (площади, характеризующие эти вероятности, заштрихованы). Полная площадь под кривой распределения всегда равна 1, т. е. полной вероятности.
Учитывая это, можно утверждать, что погрешности, абсолютные значения которых превышают появляются с вероятностью, равной 1 — Р, которая при меньше, чем при . Следовательно, чем меньше , тем реже встречаются большие погрешности, тем точнее выполнены измерения. Таким образом, Среднее квадратическое отклонение можно использовать для характеристики точности измерений:
Равномерный закон распределения. Если погрешность измерений с одинаковой вероятностью может принимать любые значения, не выходящие за некоторые границы, то такая погрешность описывается равномерным законом распределения. При этом плотность вероятности погрешности ω(Δx) постоянна внутри этих границ и равна нулю вне этих границ. Равномерный закон распределения представлен на рис. 2. Аналитически он может быть записан так:
при –Δx1 ≤ Δx ≤ + Δx1;
Рис 2. Равномерный закон распределения
С таким законом распределения хорошо согласуется погрешность от трения в опорах электромеханических приборов, не-исключенные остатки систематических погрешностей, погрешность дискретности в цифровых приборах.
Трапециевидный закон распределения. Это распределение графически изображено на рис.3, а. Погрешность имеет такой закон распределения, если она образуется из двух независимых составляющих, каждая из которых имеет равномерный закон распределения, но ширина интервала равномерных законов различна. Например, при последовательном соединении двух измерительных преобразователей, один из которых имеет погрешность, равномерно распределенную в интервале ±Δx1, а другой — равномерно распределенную в интервале ± Δx2, суммарная погрешность преобразования будет описываться трапециевидным законом распределения.
Треугольный закон распределения (закон Симпсона). Это распределение (см. рис.3, б) является частным случаем трапециевидного, когда составляющие имеют одинаковые равномерные законы распределения.
Двухмодальные законы распределения. В практике измерений встречаются двухмодальные законы распределения, т. е. законы распределения, имеющие два максимума плотности вероятности. В двухмодальный закон распределения, который может быть в приборах, имеющих погрешность от люфта кинематических механизмов или от гистерезиса при перемагничивании деталей прибора.
Рис.3. Трапециевидный (а) и треугольный (б) законы распределения
Источник
