Какими свойствами обладает нормальное распределение результатов измерений

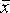
Норма́льное распределе́ние[1][2], также называемое распределением Гаусса или Гаусса — Лапласа[3] — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса:

где параметр  — математическое ожидание (среднее значение), медиана и мода распределения, а параметр  — среднеквадратическое отклонение ( — дисперсия) распределения.

Таким образом, одномерное нормальное распределение является двухпараметрическим семейством распределений, которое принадлежит экспоненциальному классу распределений.[4] Многомерный случай описан в статье «Многомерное нормальное распределение».

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием и стандартным отклонением .

Общие сведения[править | править код]

Если величина является суммой многих случайных слабо взаимозависимых величин, каждая из которых вносит малый вклад относительно общей суммы, то центрированное и нормированное распределение такой величины при достаточно большом числе слагаемых стремится к нормальному распределению.

Это следует из центральной предельной теоремы теории вероятностей. В окружающем нас мире часто встречаются величины, значение которых определяется совокупностью многих независимых факторов. Этот факт, а также то, что распределение считалось типичным, обычным, привели к тому, что в конце XIX века стал использоваться термин «нормальное распределение». Нормальное распределение играет заметную роль во многих областях науки, например в математической статистике и статистической физике.

Случайная величина, имеющая нормальное распределение, называется нормальной, или гауссовской, случайной величиной.

Определения[править | править код]

Стандартное нормальное распределение[править | править код]

Наиболее простой случай нормального распределения — стандартное нормальное распределение — частный случай, когда и . Его плотность вероятности равна

Множитель в выражении обеспечивает условие нормировки интеграла .[5] Поскольку множитель в экспоненте обеспечивает единичную дисперсию (то есть дисперсия равна единице), то и стандартное отклонение равно 1. Функция симметрична в точке , её значение в ней максимально и равно . Точки перегиба функции — и .

Гаусс называл стандартным нормальным распределение с , то есть

Нормальное распределение с параметрами [править | править код]

Каждое нормальное распределение — это вариант стандартного нормального распределения, область значений которого растягивается множителем (стандартное отклонение) и переносится на (математическое ожидание):

являются параметрами нормального распределения. Плотность вероятности должна нормироваться , так что интеграл равен 1.

Если  — стандартная нормальная случайная величина, то величина будет иметь нормальное распределение с математическим ожиданием и стандартным отклонением . Наоборот, если  — нормальная величина с параметрами и , то будет иметь стандартное нормальное распределение.

Если в экспоненте плотности вероятности раскрыть скобки и учитывать, что , то

Таким образом, плотность вероятности каждого нормального распределения представляет собой экспоненту квадратичной функции:

где . Отсюда можно выразить среднее значение как , а дисперсию как . Для стандартного нормального распределения , и .

Обозначение[править | править код]

Плотность вероятности стандартного нормального распределения (с нулевым средним и единичной дисперсией) часто обозначается греческой буквой (фи) [6]. Также достаточно часто используется альтернативная формы греческой буквы фи .

Нормальное распределение часто обозначается , или .[7] Если случайная величина распределена по нормальному закону со средним и вариацией , то пишут

Функция распределения[править | править код]

Функция распределения стандартного нормального распределения обычно обозначается заглавной греческой буквой (фи) и представляет собой интеграл

С ней связана функция ошибок (интеграл вероятности) , дающий вероятность того, что нормальная случайная величина со средним 0 и вариацией 1/2 попадёт в отрезок :

Эти интегралы, неберущиеся в элементарных функциях, и называются специальными функциями. Многие их численные приближения известны. См. ниже.

Функции связаны, в частности, соотношением

Нормальное распределение с плотностью , средним и отклонением имеет следующую функцию распределения:

Можно использовать функцию  — она даст вероятность того, что значение стандартной нормальной случайной величины превысит : .

График стандартной нормальной функции распределения имеет 2-кратную вращательную симметрию относительно точки (0,1/2), то есть . Её неопределенный интеграл равен

Функция распределения стандартной нормальной случайной величины может быть разложена с помощью интегрирования по частям в ряд:

где знак означает двойной факториал.

Асимптотическое разложение функции распределения для больших может быть также произведено интегрированием по частям.

Стандартное отклонение[править | править код]

Около 68 % значений из нормального распределения находятся на расстоянии не более одного стандартного отклонения σ от среднего; около 95 % значений лежат расстоянии не более двух стандартных отклонений; и 99,7 % не более трёх. Этот факт является частным случаем правила 3 сигм для нормальной выборки.

Более точно, вероятность получить нормальное число в интервале между и равна

Если рассматривать 12 значимых символов, значения для равны:[8]

Свойства[править | править код]

Моменты[править | править код]

Моментами и абсолютными моментами случайной величины называются математические ожидания случайных величин и , соответственно. Если математическое ожидание случайной величины , то эти параметры называются центральными моментами. В большинстве случаев представляют интерес моменты для целых .

Если имеет нормальное распределение, то для неё существуют (конечные) моменты при всех с действительной частью больше −1. Для неотрицательных целых , центральные моменты таковы:

Здесь  — натуральное число, а запись означает двойной факториал числа , то есть (поскольку в данном случае нечётно) произведение всех нечётных чисел от 1 до .

Центральные абсолютные моменты для неотрицательных целых таковы:

Последняя формула справедлива также для произвольных .

Преобразование Фурье и характеристическая функция[править | править код]

Преобразование Фурье нормальной плотности вероятности с математическим ожиданием стандартным отклонением равно[9]

где есть мнимая единица. Если математическое ожидание , то первый множитель равен 1, и преобразование Фурье, не считая константу, есть нормальная плотность вероятности на частотных интервалах, с математическим ожиданием равным 0 и стандартным отклонением . В частности, стандартное нормальное распределение есть собственная функция от преобразования Фурье.

В теории вероятности, преобразование Фурье плотности распределения действительной случайной величины близко связано с характеристической функцией этой величины, которая определена как математическое ожидание от и является функцией вещественной переменной (частотный параметр преобразования Фурье). Определение может быть распространено и на комплексную переменную .[10] Соотношение записывается так:

Бесконечная делимость[править | править код]

Нормальное распределение является бесконечно делимым.

Если случайные величины и независимы и имеют нормальное распределение с математическими ожиданиями и и дисперсиями и соответственно, то также имеет нормальное распределение с математическим ожиданием и дисперсией
Отсюда вытекает, что нормальная случайная величина представима как сумма произвольного числа независимых нормальных случайных величин.

Максимальная энтропия[править | править код]

Нормальное распределение имеет максимальную дифференциальную энтропию среди всех непрерывных распределений, дисперсия которых не превышает заданную величину[11][12].

Правило трёх сигм для гауссовской случайной величины[править | править код]

Правило трёх сигм () — практически все значения нормально распределённой случайной величины лежат в интервале , где  — математическое ожидание и параметр нормальной случайной величины. Более точно — приблизительно с вероятностью 0,9973 значение нормально распределённой случайной величины лежит в указанном интервале.

Моделирование нормальных псевдослучайных величин[править | править код]

При компьютерном моделировании, особенно при применении метода Монте-Карло, желательно использовать величины, распределенные по нормальному закону. Многие алгоритмы дают стандартные нормальные величины, так как нормальную величину можно получить как , где Z — стандартная нормальная величина. Алгоритмы также используют различные преобразования равномерных величин.
Простейшие приближённые методы моделирования основываются на центральной предельной теореме. Если сложить достаточно большое количество независимых одинаково распределённых величин с конечной дисперсией, то сумма будет иметь распределение, близкое к нормальному. Например, если сложить 100 независимых стандартно равномерно распределённых случайных величин, то распределение суммы будет приближённо нормальным.

Для программного генерирования нормально распределённых псевдослучайных величин предпочтительнее использовать преобразование Бокса — Мюллера. Оно позволяет генерировать одну нормально распределённую величину на базе одной равномерно распределённой.

Также существует алгоритм Зиккурат, который работает даже быстрее преобразования Бокса — Мюллера. Тем не менее, сложнее в реализации, но его применение оправдано в случаях, когда требуется генерирование очень большого числа неравномерно распределённых случайных чисел.

Нормальное распределение в природе и приложениях[править | править код]

Нормальное распределение часто встречается в природе. Например, следующие случайные величины хорошо моделируются нормальным распределением:

• отклонение при стрельбе;
• погрешности измерений (однако погрешности некоторых измерительных приборов имеют иное распределение);
• некоторые характеристики живых организмов в популяции.

Такое широкое распространение этого распределения связано с тем, что оно является бесконечно делимым непрерывным распределением с конечной дисперсией. Поэтому к нему в пределе приближаются некоторые другие, например биномиальное и пуассоновское. Этим распределением моделируются многие недетерминированные физические процессы[13].

Многомерное нормальное распределение используется при исследовании многомерных случайных величин (случайных векторов). Одним из многочисленных примеров таких приложений является исследование параметров личности человека в психологии и психиатрии.

Связь с другими распределениями[править | править код]

• Нормальное распределение является распределением Пирсона типа XI[14].
• Отношение пары независимых стандартных нормально распределенных случайных величин имеет распределение Коши[15]. То есть, если случайная величина представляет собой отношение (где и  — независимые стандартные нормальные случайные величины), то она будет обладать распределением Коши.
• Если  — совместно независимые стандартные нормальные случайные величины, то есть , то случайная величина имеет распределение хи-квадрат с k степенями свободы.
• Если случайная величина подчинена логнормальному распределению, то её натуральный логарифм имеет нормальное распределение. То есть, если , то . И наоборот, если , то .
• Если независимые нормально распределенные случайные величины с математическими ожиданиями и дисперсиями , то их выборочное среднее независимо от выборочного стандартного отклонения,[16] а отношение следующих двух величин будет иметь t-распределение с степенями свободы:

• Отношение квадратов двух стандартных нормальных случайных величин имеет распределение Фишера со степенями свободы .

История[править | править код]

Впервые нормальное распределение как предел биномиального распределения при появилось в 1738 году во втором издании работы Муавра «Доктрина случайностей»[en][18]. Это было первое доказательство частного случая центральной предельной теоремы. В 1809 году Гаусс в сочинении «Теория движения небесных тел» ввёл это распределение как возникающее в результате многократных измерений движения небесных тел. Однако Гаусс вывел формулу для действительных случайных величин из принципа достижения максимума совместной плотности всех измерений в точке с координатами, равными среднему всех измерений. Этот принцип впоследствии подвергался критике. В 1812 году Лаплас в теореме Муавра — Лапласа обобщил результат Муавра для произвольного биномиального распределения, то есть для сумм одинаково распределённых независимых бинарных величин[3].

См. также[править | править код]

• Аддитивный белый гауссовский шум
• Логнормальное распределение
• Равномерное распределение
• Центральная предельная теорема
• Двумерное нормальное распределение
• Многомерное нормальное распределение
• Распределение хи-квадрат
• Статистический критерий
• Частотное распределение

Примечания[править | править код]

Литература[править | править код]

• Королюк В. С., Портенко Н. И., Скороход А. В., Турбин А. Ф. Справочник по теории вероятностей и математической статистике. — М.: Наука, 1985. — 640 с.
• Halperin, Max; Hartley, Herman O.; Hoel, Paul G. Recommended Standards for Statistical Symbols and Notation. COPSS Committee on Symbols and Notation (англ.) // The American Statistician (англ.)русск. : journal. — 1965. — Vol. 19, no. 3. — P. 12—14. — doi:10.2307/2681417.
• McPherson, Glen. Statistics in Scientific Investigation: Its Basis, Application and Interpretation (англ.). — Springer-Verlag, 1990. — ISBN 978-0-387-97137-7.
• Bryc, Wlodzimierz. The Normal Distribution: Characterizations with Applications (англ.). — Springer-Verlag, 1995. — ISBN 978-0-387-97990-8.

Ссылки[править | править код]

• Таблица значений функции стандартного нормального распределения
• Онлайн расчёт вероятности нормального распределения