Какими свойствами обладает катушка с током
Приветствую всех на нашем сайте!
Мы продолжаем изучать электронику с самых основ, и темой сегодняшней статьи будет катушка индуктивности. Забегая вперед скажу, что сначала мы обсудим теоретические аспекты, а несколько будущих статей посвятим целиком и полностью рассмотрению различных электрических схем, в которых используются катушки индуктивности, а также элементы, которые мы изучили ранее в рамках нашего курса – резисторы и конденсаторы.
Устройство и принцип работы катушки индуктивности.
Как уже понятно из названия элемента – катушка индуктивности, в первую очередь, представляет из себя именно катушку ???? То есть большое количество витков изолированного проводника. Причем наличие изоляции является важнейшим условием – витки катушки не должны замыкаться друг с другом. Чаще всего витки наматываются на цилиндрический или тороидальный каркас:

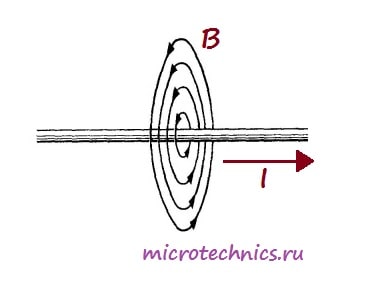
Важнейшей характеристикой катушки индуктивности является, естественно, индуктивность, иначе зачем бы ей дали такое название ???? Индуктивность – это способность преобразовывать энергию электрического поля в энергию магнитного поля. Это свойство катушки связано с тем, что при протекании по проводнику тока вокруг него возникает магнитное поле:
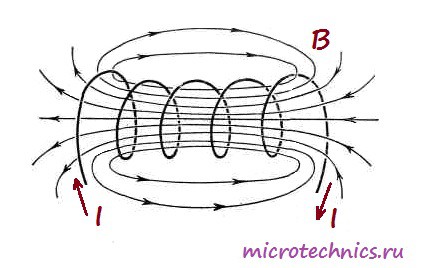
А вот как выглядит магнитное поле, возникающее при прохождении тока через катушку:
В общем то, строго говоря, любой элемент в электрической цепи имеет индуктивность, даже обычный кусок провода. Но дело в том, что величина такой индуктивности является очень незначительной, в отличие от индуктивности катушек. Собственно, для того, чтобы охарактеризовать эту величину используется единица измерения Генри (Гн). 1 Генри – это на самом деле очень большая величина, поэтому чаще всего используются мкГн (микрогенри) и мГн (милигенри). Величину индуктивности катушки можно рассчитать по следующей формуле:
L = frac{mu_0thinspace mu S N^2}{l}
Давайте разберемся, что за величину входят в это выражение:
- mu_0 – магнитная проницаемость вакуума. Это табличная величина (константа) и равна она следующему значению: mu_0 = 4 pi cdot 10^{-7}medspacefrac{Гн}{м}
- mu – магнитная проницаемость магнитного материала сердечника. А что это за сердечник и для чего он нужен? Сейчас выясним. Дело все в том, что если катушку намотать не просто на каркас (внутри которого воздух), а на магнитный сердечник, то индуктивность возрастет многократно. Посудите сами – магнитная проницаемость воздуха равна 1, а для никеля она может достигать величины 1100. Вот мы и получаем увеличение индуктивности более чем в 1000 раз
- S – площадь поперечного сечения катушки
- N – количество витков
- l – длина катушки
Из формулы следует, что при увеличении числа витков или, к примеру, диаметра (а соответственно и площади поперечного сечения) катушки, индуктивность будет увеличиваться. А при увеличении длины – уменьшаться. Таким образом, витки на катушке стоит располагать как можно ближе друг к другу, поскольку это приведет к уменьшению длины катушки.
С устройством катушки индуктивности мы разобрались, пришло время рассмотреть физические процессы, которые протекают в этом элементе при прохождении электрического тока. Для этого мы рассмотрим две схемы – в одной будем пропускать через катушку постоянный ток, а в другой -переменный!
Катушка индуктивности в цепи постоянного тока.
Итак, в первую очередь, давайте разберемся, что же происходит в самой катушке при протекании тока. Если ток не изменяет своей величины, то катушка не оказывает на него никакого влияния. Значит ли это, что в случае постоянного тока использование катушек индуктивности и рассматривать не стоит? А вот и нет ???? Ведь постоянный ток можно включать/выключать, и как раз в моменты переключения и происходит все самое интересное. Давайте рассмотрим цепь:

Резистор выполняет в данном случае роль нагрузки, на его месте могла бы быть, к примеру, лампа. Помимо резистора и индуктивности в цепь включены источник постоянного тока и переключатель, с помощью которого мы будем замыкать и размыкать цепь. Что же произойдет в тот момент когда мы замкнем выключатель?
Ток через катушку начнет изменяться, поскольку в предыдущий момент времени он был равен 0. Изменение тока приведет к изменению магнитного потока внутри катушки, что, в свою очередь, вызовет возникновение ЭДС (электродвижущей силы) самоиндукции, которую можно выразить следующим образом:
varepsilon_s = -frac{dPhi}{dt}
Возникновение ЭДС приведет к появлению индукционного тока в катушке, который будет протекать в направлении, противоположном направлению тока источника питания. Таким образом, ЭДС самоиндукции будет препятствовать протеканию тока через катушку (индукционный ток будет компенсировать ток цепи из-за того, что их направления противоположны). А это значит, что в начальный момент времени (непосредственно после замыкания выключателя) ток через катушку I_L будет равен 0. В этот момент времени ЭДС самоиндукции максимальна. А что же произойдет дальше? Поскольку величина ЭДС прямо пропорциональна скорости изменения тока, то она будет постепенно ослабевать, а ток, соответственно, наоборот будет возрастать. Давайте посмотрим на графики, иллюстрирующие то, что мы обсудили:
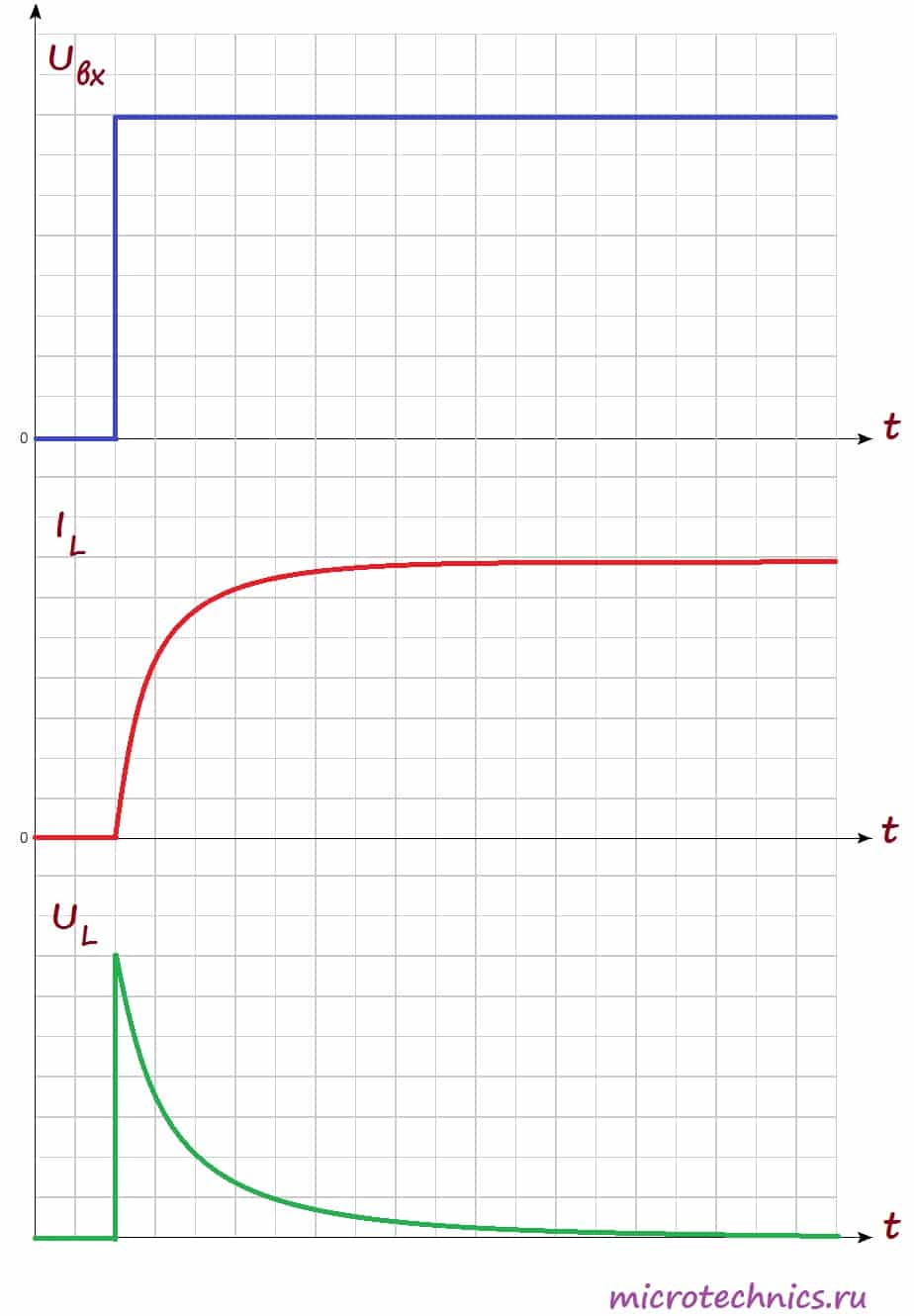
На первом графике мы видим входное напряжение цепи – изначально цепь разомкнута, а при замыкании переключателя появляется постоянное значение. На втором графике мы видим изменение величины тока через катушку индуктивности. Непосредственно после замыкания ключа ток отсутствует из-за возникновения ЭДС самоиндукции, а затем начинает плавно возрастать.
Напряжение на катушке наоборот в начальный момент времени максимально, а затем уменьшается. График напряжения на нагрузке будет по форме (но не по величине) совпадать с графиком тока через катушку (поскольку при последовательном соединении ток, протекающий через разные элементы цепи одинаковый). Таким образом, если в качестве нагрузки мы будем использовать лампу, то они загорится не сразу после замыкания переключателя, а с небольшой задержкой (в соответствии с графиком тока).
Аналогичный переходный процесс в цепи будет наблюдаться и при размыкании ключа. В катушке индуктивности возникнет ЭДС самоиндукции, но индукционный ток в случае размыкания будет направлен в том же самом направлении, что и ток в цепи, а не в противоположном, поэтому запасенная энергия катушки индуктивности пойдет на поддержание тока в цепи:
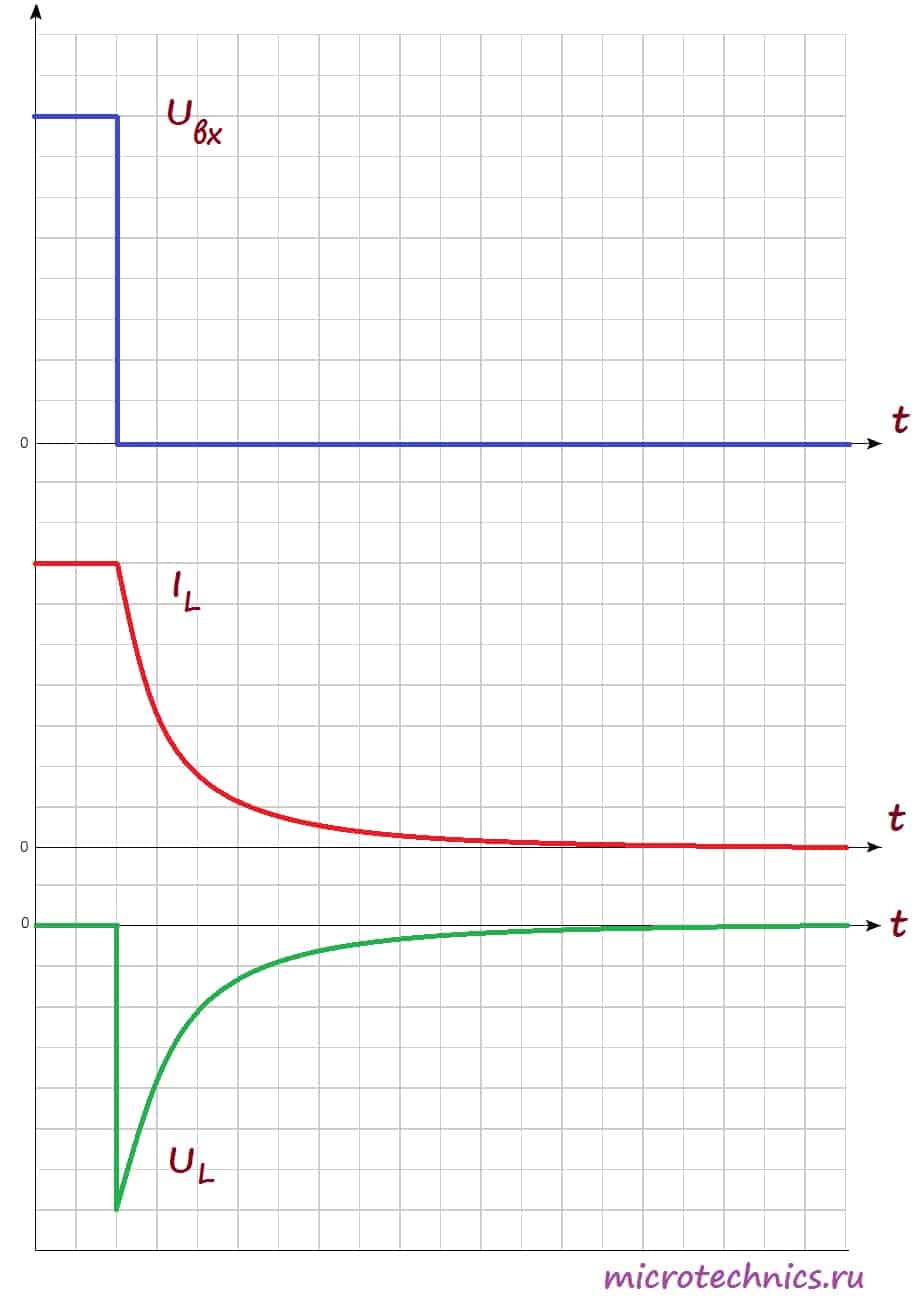
После размыкания ключа возникает ЭДС самоиндукции, которая препятствует уменьшению тока через катушку, поэтому ток достигает нулевого значения не сразу, а по истечении некоторого времени. Напряжение же в катушке по форме идентично случаю замыкания переключателя, но противоположно по знаку. Это связано с тем, что изменение тока, а соответственно и ЭДС самоиндукции в первом и втором случаях противоположны по знаку (в первом случае ток возрастает, а во втором убывает).
Кстати, я упомянул, что величина ЭДС самоиндукции прямо пропорциональна скорости изменения силы тока, так вот, коэффициентом пропорциональности является ни что иное как индуктивность катушки:
varepsilon_s = -Lmedspacefrac{dI}{dt}
На этом мы заканчиваем с катушками индуктивности в цепях постоянного тока и переходим к цепям переменного тока.
Катушка индуктивности в цепи переменного тока.
Рассмотрим цепь, в которой на катушку индуктивности подается переменный ток:
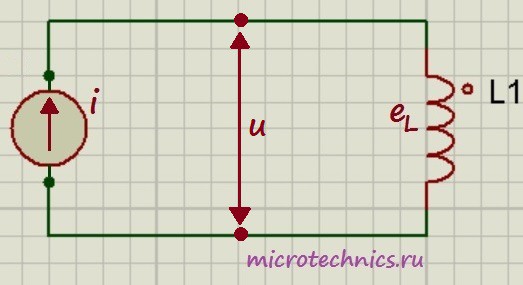
Давайте посмотрим на зависимости тока и ЭДС самоиндукции от времени, а затем уже разберемся, почему они выглядят именно так:
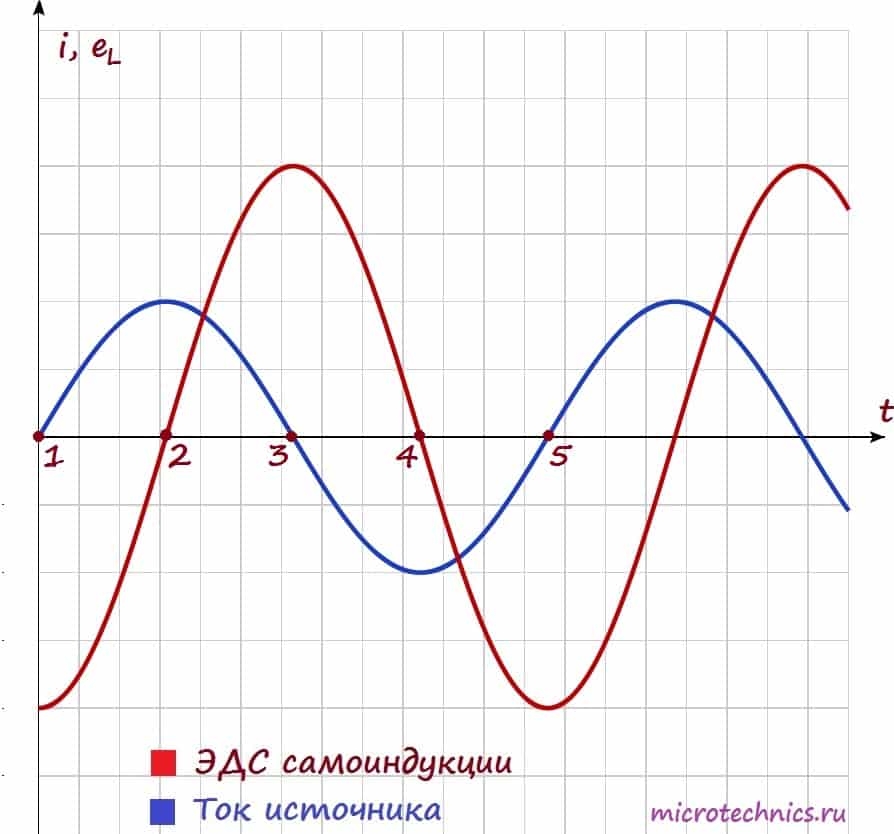
Как мы уже выяснили ЭДС самоиндукции у нас прямо пропорциональна и противоположна по знаку скорости изменения тока:
varepsilon_L = -Lmedspacefrac{dI}{dt}
Собственно, график нам и демонстрирует эту зависимость! Смотрите сами – между точками 1 и 2 ток у нас изменяется, причем чем ближе к точке 2, тем изменения меньше, а в точке 2 в течении какого-то небольшого промежутка времени ток и вовсе не изменяет своего значения. Соответственно скорость изменения тока максимальна в точке 1 и плавно уменьшается при приближении к точке 2, а в точке 2 равна 0, что мы и видим на графике ЭДС самоиндукции. Причем на всем промежутке 1-2 ток возрастает, а значит скорость его изменения положительна, в связи с этим на ЭДС на всем этом промежутке напротив принимает отрицательные значения.
Аналогично между точками 2 и 3 – ток уменьшается – скорость изменения тока отрицательная и увеличивается – ЭДС самоиндукции увеличивается и положительна. Не буду расписывать остальные участки графика – там все процессы протекают по такому же принципу ????
Кроме того, на графике можно заметить очень важный момент – при увеличении тока (участки 1-2 и 3-4) ЭДС самоиндукции и ток имеют разные знаки (участок 1-2: varepsilon < 0, i > 0, участок 3-4: varepsilon > 0, i < 0). Таким образом, ЭДС самоиндукции препятствует возрастанию тока (индукционные токи направлены “навстречу” току источника).
А на участках 2-3 и 4-5 все наоборот – ток убывает, а ЭДС препятствует убыванию тока (поскольку индукционные токи будут направлены в ту же сторону, что и ток источника и будут частично компенсировать уменьшение тока).
И в итоге мы приходим к очень интересному факту – катушка индуктивности оказывает сопротивление переменному току, протекающему по цепи. А значит она имеет сопротивление, которое называется индуктивным или реактивным и вычисляется следующим образом:
X_L = wmedspace L
Где w – круговая частота: w = 2 pi f. [/latex]f[/latex] – это частота переменного тока. Таким образом, чем больше частота тока, тем большее сопротивление будет ему оказывать катушка индуктивности. А если ток постоянный (f = 0), то реактивное сопротивление катушки равно 0, соответственно, она не оказывает влияния на протекающий ток.
Давайте вернемся к нашим графикам, которые мы построили для случая использования катушки индуктивности в цепи переменного тока. Мы определили ЭДС самоиндукции катушки, но каким же будет напряжение u? Здесь все на самом деле просто! По 2-му закону Кирхгофа:
u + varepsilon_L = 0
А следовательно:
u = – varepsilon_L
Построим на одном графике зависимости тока и напряжения в цепи от времени:

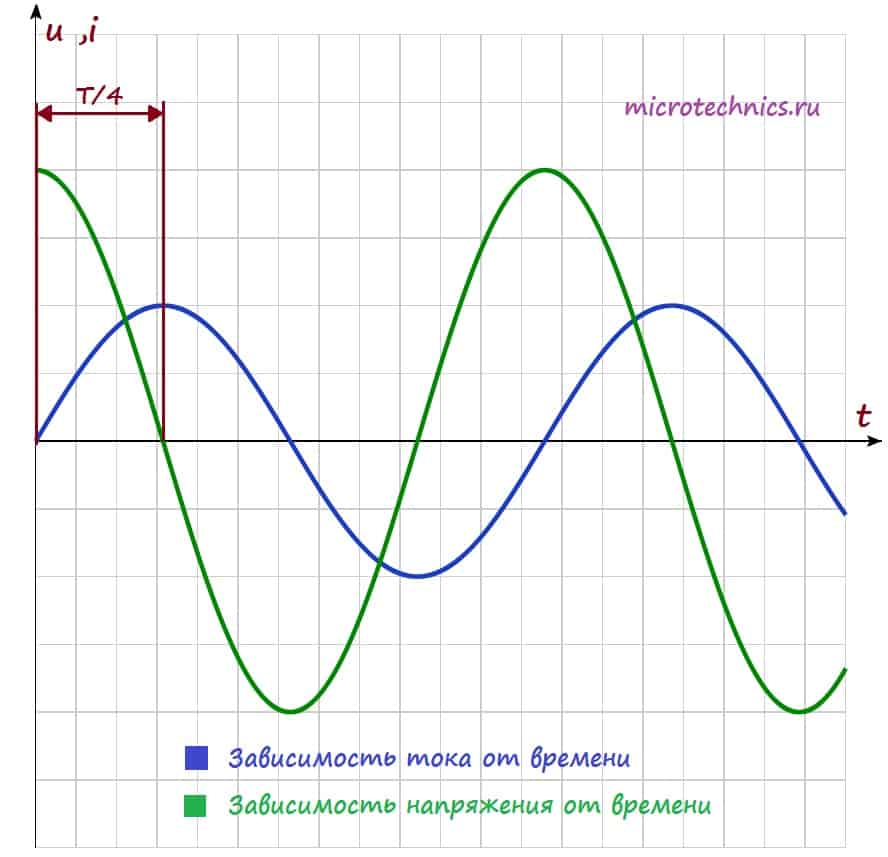
Как видите ток и напряжение сдвинуты по фазе (ссылка) друг относительно друга, и это является одним из важнейших свойств цепей переменного тока, в которых используется катушка индуктивности:
При включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между напряжением и током, при этом ток отстает по фазе от напряжения на четверть периода.
Вот и с включением катушки в цепь переменного тока мы разобрались!
На этом, пожалуй, закончим сегодняшнюю статью, она получилась уже довольно объемной, поэтому разговор о катушках индуктивности мы продолжим в следующий раз. Так что до скорых встреч, будем рады видеть вас на нашем сайте!
Источник
Индукционная катушка — это дроссель или изолированный проводник. Используется электрический каркас, композитные вставки. При рассмотрении понятия необходимо изучить свойства, основные особенности катушки индуктивности.
Определение устройства
Катушка индуктивности — это устройство, которое обладает малой емкостью и значительным сопротивлением. Дроссель является отменным проводником электрического тока, учитывается высокий показатель инерционности. Устройства применяются в качестве свернутого изолированного проводника. Винтовые, спиральные модификации способны справляться с помехами, колебаниями в сети.
 Индукционная катушка
Индукционная катушка
Важно! Устройство работает в цепях переменного тока при низкой и высокой частоте.
Назначение и принцип действия
Специалисты задаются вопросом, зачем нужна токовая катушка индуктивности в цепи, и для этого необходимо разобраться в показателях. Коэффициент ЭДС (электродвижущая сила) показывает разницу между энергией и магнитным потоком. Устройства самоиндукции способны влиять на изменения в цепи. Чаще всего дроссели применяются в силовых установках. Они способны контролировать уровень напряжения, не допускают разрыва цепи.
 Устройства самоиндукции
Устройства самоиндукции
Также компоненты устанавливаются на пару с конденсаторами либо резисторами. Благодаря работе катушки фильтры находятся в безопасности. Теперь вызывает интерес, как включается индукционная катушка. Принцип работы построен на изоляции проводников. В конструкции используется электрический каркас с различным сечением. За счёт намоток обеспечивается распределение ёмкости на дросселе.
Интересно! Витки наматываются с определенным шагом, многое зависит от типа катушки.
Виды и типы
Различают низкочастотные, высокочастотные модели. В отдельную категорию выделяют винтовые, спиральные катушки. Также существуют модификации, которые используются в радиотехнике. Они подходят для защиты конденсатора либо резонансных контуров.
 Устройства в радиотехнике
Устройства в радиотехнике
Для трансформаторов годятся катушки с усилителем каскадом. В последнюю категорию выделены вариометры, основное отличие — высокая частота колебательных контуров. Дроссели могут быть одинарными либо сдвоенными. От этого зависит показатель индуктивности и питания системы.
Низкочастотные
Для включения в электрическую цепь, применяется низкочастотная катушка индуктивности. Она предназначена для подавления переменного тока. В формуле учитывается циклическая частота и показатели индуктивности. За основу в устройствах берётся сердечник, который изготавливается из стали. Он может быть с фильтрами либо без них.
Чтобы влиять на частоту, происходит игра с сопротивлением. В цепи постоянного тока напряжение должно быть неизменным. С целью понижения частоты применяются фильтры. Основная проблема — это малая ёмкость. Чтобы детально ознакомиться с дросселем, стоит подробнее узнать о резонансной частоте, которая выделяется на контуре рабочего сигнала.
Когда в цепях повышается напряжение, на каркас оказывается нагрузка. В цепи постоянного тока задействуются непрозрачные проволочные резисторы. Также для этих целей подходят однослойные катушки типа «универсал». Их особенность — использование ферритовых стержней.
 Низкочастотная катушка
Низкочастотная катушка
Высокочастотные
Устройства изготавливаются с различными типами обмотки. Речь идет о наборе преимуществ, которые спасают в той или иной ситуации. Сфера применения элементов широка, учитывается значительная частота модуляции. Таким образом удается бороться с повышенным сопротивлением металлов. У катушек имеется сердечник.
Основная задача — это модуляция частоты генератора. Она происходит за счёт усиления сигнала, и за процессом можно проследить при подключении осциллографа. Многие высокочастотные катушки не отличаются стабильной работой, поскольку применяется керамический каркас. У него малый срок годности, плюс они восприимчивы к повышенной влажности.
Интересно! Современные товары изготавливаются из алюминия и являются компактными.
Электрикам известны контурные, безконтурные модификации высокой частоты. В зависимости от намотки учитывается стабильность электрических параметров. У моделей высокой частоты могут применяться магниты и провода. Речь идет о порошковых материалах, сделанных из диэлектриков.
Процесс изготовления связан с методом холодного прессования. Индуктивные датчики отличаются по защищенности. На предприятиях элементы могут погружать в раствор либо продевать в трубку. Это делается с целью избежания коротких замыканий. Мировые производители решают проблему путем использование вторичного витка.
 Высокочастотная катушка
Высокочастотная катушка
У моделей значительное сопротивление и есть проблема с концентрацией электролита. Таким образом изменяются свойства катушки индуктивности. Проводимость раствора падает и повышается частота электромагнитного поля.
Основные технические параметры
Катушки индуктивности имеют следующие характеристики:
- добротность отклонения;
- эффективность;
- начальная индуктивность;
- температура;
- стабильность;
- предельная емкость;
- номинальная индуктивность.
Стабильность демонстрирует свойства устройства при изменении условий использования. Температура фиксируется вследствие различных причин. Многое зависит от размера каркаса. Когда температура уменьшается, индуктивность также снижается. Современные параметры — это цикличность, которая является отношением температуры к линейному расширению. Учитывается изменение в керамической основе плюс показатель плотности.
Температура отслеживается на горячей намотке. В этом плане хорошо себя показали многослойные дроссели с сердечником, которые сделаны из карбонильного железа. Ёмкость отображает количество витков катушки, берется в расчет количество секций и контуров. Высокочастотные модели считаются более емкостными и стабильными.
 Емкостные катушки
Емкостные катушки
Номинальная индуктивность — это параметр, который учитывает изменение размеров волны. Измерение происходит в микрогенрах. Если смотреть на формулу, учитывается количество витков, длина намотки, плюс диаметр катушки.
Маркировка
При рассмотрении катушек индуктивности оценивается цветовая и кодовая маркировка. Если смотреть на первые цифры, отображается показатель индуктивности. Далее учитывается параметр отклонения:
- Серебряный 0,01 мкГн, 10%.
- Золотой 0,1 мкГн, 5%.
- Черный 0,1мкГн, 20%.
- Коричневый 1,1 мкГн.
- Красный 2, 2 мкГн.
- Оранжевый 1 мкГн.
- Желтый 4 мкГн.
- Зеленый 5 мкГн.
- Голубой 6 мкГн.
- Фиолетовый 7мкГн.
- Серый 8 мкГн.
- Белый 9 мкГн.
 Маркировка
Маркировка
В нестабильной цепи переменного электрического тока не обойтись без катушки индуктивности. Выше описаны основные типы изолированных проводников, продемонстрированы их параметры. Учитывается уровень частоты, а также свойства.
Источник
Что такое катушка индуктивности
Что вы себе представляете под словом “катушка” ? Ну… это, наверное, какая-нибудь “фиговинка”, на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции.
Изоляция может быть из бесцветного лака, из ПВХ-изоляции и даже из матерчатой. Тут фишка такая, что хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности своими руками, ни в коем случае не вздумайте брать обычный медный голый провод!
Индуктивность
Любая катушка индуктивности обладает индуктивностью. Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется с помощью LC – метра.
Что такое индуктивность? Если через провод пропустить электрический ток, то он вокруг себя создаст магнитное поле:
где
В – магнитное поле, Вб
I – сила тока, А
А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы напряжение
И у нас получится вот такая картина с магнитными силовыми линиями:
Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, в нашем случае площадь цилиндра, тем больше будет магнитный поток (Ф). Так как через катушку течет электрический ток, значит, через нее проходит ток с Силой тока (I), а коэффициент между магнитным потоком и силой тока называется индуктивностью и вычисляется по формуле:
С научной же точки зрения, индуктивность – это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается , то магнитное поле сжимается.
Самоиндукция
Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение.
Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. Согласно Закону Ома:
где
I – сила тока в катушке , А
U – напряжение в катушке, В
R – сопротивление катушки, Ом
Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки для постоянного тока также постоянное.
И второй феномен в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности – источник тока, то у нас ЭДС самоиндукции будет суммироваться к напряжению, которое мы уже подали на катушку.
То есть как только мы разрываем цепь, на катушке напряжение в этот момент может быть в разы больше, чем было до размыкания цепи, а сила тока в цепи катушки будет тихонько падать, так как ЭДС самоиндукции будет поддерживать убывающее напряжение.
Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока будет плавно убывать до нуля. Короче говоря, сила тока в катушке мгновенно измениться не может.
Типы катушек индуктивности
Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником.
Но где у нее сердечник? Воздух – это немагнитный сердечник :-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллигенри.
А вот катушки индуктивности с сердечником:
В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.
Для катушек средней индуктивности используются ферритовые сердечники:
Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но с одной обмоткой, в отличие от трансформатора.
Дроссель
Также есть особый вид катушек индуктивностей. Это так называемые дроссели. Дроссель – это катушка индуктивности, задача которой состоит в том, чтобы создать в цепи большое сопротивление для переменного тока, чтобы подавить токи высоких частот.
Постоянный ток через дроссель проходит без проблем. Почему это происходит, можете прочитать в этой статье. Обычно дроссели включаются в цепях питания усилительных устройств. Дроссели предназначены для защиты источников питания от попадания в них высокочастотных сигналов (ВЧ-сигналов). На низких частотах (НЧ) они используются в фильтрах цепей питания и обычно имеют металлические или ферритовые сердечники. Ниже на фото силовые дроссели:

Также существует еще один особый вид дросселей – это сдвоенный дроссель. Он представляет из себя две встречно намотанных катушки индуктивности. За счет встречной намотки и взаимной индукции он более эффективен. Сдвоенные дроссели получили широкое распространение в качестве входных фильтров блоков питания, а также в звуковой технике.

Что влияет на индуктивность?
От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC – метр мне показывает ноль.
Имеется ферритовый сердечник
Начинаю вводить катушку в сердечник на самый край
LC-метр показывает 21 микрогенри.
Ввожу катушку на середину феррита
35 микрогенри. Уже лучше.
Продолжаю вводить катушку на правый край феррита
20 микрогенри. Делаем вывод, самая большая индуктивность на цилиндрическом феррите возникает в его середине. Поэтому, если будете мотать на цилиндрике, старайтесь мотать в середине феррита. Это свойство используется для плавного изменения индуктивности в переменных катушках индуктивности:
где
1 – это каркас катушки
2 – это витки катушки
3 – сердечник, у которого сверху пазик под маленькую отвертку. Вкручивая или выкручивая сердечник, мы тем самым изменяем индуктивность катушки.
Экспериментируем дальше. Давайте попробуем сжимать и разжимать витки катушки. Для начала ставим ее в середину и начинаем сжимать витки
Индуктивность стала почти 50 микрогенри!
А давайте-ка попробуем расправим витки по всему ферриту
13 микрогенри. Делаем вывод: для максимальной индуктивности мотать катушку надо “виток к витку”.
Убавим витки катушки в два раза. Было 24 витка, стало 12.
Совсем маленькая индуктивность. Убавил количество витков в 2 раза, индуктивность уменьшилась в 10 раз. Вывод: чем меньше количество витков – тем меньше индуктивность и наоборот. Индуктивность меняется не прямолинейно виткам.
Давайте поэкспериментируем с ферритовым кольцом.
Замеряем индуктивность
15 микрогенри
Отдалим витки катушки друг от друга
Замеряем снова
Хм, также 15 микрогенри. Делаем вывод: расстояние от витка до витка не играет никакой роли в катушке индуктивности тороидального исполнения.
Мотнем побольше витков. Было 3 витка, стало 9.
Замеряем
Офигеть! Увеличил количество витков в 3 раза, а индуктивность увеличилась в 12 раз! Вывод: индуктивность меняется не прямолинейно виткам.
Если верить формулам для расчета индуктивностей, индуктивность зависит от “витков в квадрате”. Эти формулы я здесь выкладывать не буду, потому как не вижу надобности. Скажу только, что индуктивность зависит еще от таких параметров, как сердечник (из какого материала он сделан), площадь поперечного сечения сердечника, длина катушки.
Обозначение на схемах
Последовательное и параллельное соединение катушек индуктивности
При последовательном соединении индуктивностей, их общая индуктивность будет равняться сумме индуктивностей.
А при параллельном соединении получаем вот так:
При соединении индуктивностей должно выполняться правило, чтобы они были пространственно разнесены на плате. Это связано с тем, что при близком расположении друг друга их магнитные поля будут влиять с друг другом, и поэтому показания индуктивностей будут неверны. Не ставьте на одну железную ось две и более тороидальных катушек. Это может привести к неправильным показаниям общей индуктивности.
Резюме
Катушка индуктивности играет в электронике очень большую роль, особенно в приемопередающей аппаратуре. На катушках индуктивности строятся также различные фильтры для электронной радиоаппаратуры, а в электротехнике ее используют также в качестве ограничителя скачка силы тока.
Ребята из Паяльника забабахали очень неплохой видос про катушку индуктивности. Советую посмотреть в обязательном порядке:
Источник
