Какими свойствами обладает эпюр
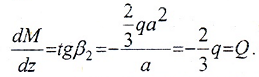
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 ноября 2017; проверки требуют 2 правки.
Запрос «Эпюр» перенаправляется сюда; см. также другие значения.
Не следует путать с Чертёж.
Не следует путать с Эпюра.
Эпю́р (фр. epure — чертёж) — чертёж, на котором пространственная фигура изображена методом нескольких (по ГОСТу трёх, но не всегда) плоскостей. Обычно оно даёт 3 вида: фронтальную, горизонтальную и профильную проекции (фасад, план, профиль). Чертёж проецируется на взаимно перпендикулярные, а затем развернутые на одну плоскости.
История[править | править код]
Сведения и приемы построений, обусловливаемые потребностью в плоских изображениях пространственных форм, накапливались постепенно еще с древних времен. В течение продолжительного периода плоские изображения выполнялись преимущественно как изображения наглядные. С развитием техники первостепенное значение приобрел вопрос о применении метода, обеспечивающего точность и удобоизмеримость изображений, то есть возможность точно установить место каждой точки изображения относительно других точек или плоскостей и путём простых приемов определить размеры отрезков линий и фигур.
Будучи одним из министров в революционном правительстве Франции, Гаспар Монж много сделал для её защиты от иностранной интервенции и для победы революционных войск. Начав с задачи точной резки камней по заданным эскизам применительно к архитектуре и фортификации, Монж пришёл к созданию методов, обобщённых им впоследствии в новой науке — начертательной геометрии, творцом которой он по праву считается. Учитывая возможность применения методов начертательной геометрии в военных целях при строительстве укреплений, руководство Мезьерской школы не допускало открытой публикации вплоть до 1799 года[1] (стенографическая запись лекций была сделана в 1795 году).
Система двух плоскостей проекции[править | править код]
рис.1 Система двух плоскостей проекций: а — расположение плоскостей проекций; б — совмещение плоскостей проекций
В данном случае, для построения изображения в двух плоскостях проекций, горизонтальная плоскость проекций П1 и фронтальная плоскость проекций П2 совмещаются в одну, как показано на рис.1. В пересечении они дают ось проекций x и делят пространство на четыре четверти (квадранта).
Система трех плоскостей проекций[править | править код]
рис.2 Система трех плоскостей проекций: а — расположение плоскостей проекций; б — совмещение плоскостей проекций
В системе трех плоскостей проекций совмещаются все три плоскости проекций (П1 — горизонтальная, П2 — фронтальная и П3 — профильная), как показано на рис.2. Плоскости образуют три оси проекций (оси координат) и восемь прямоугольных трехгранников, деля пространство на восемь октантов.
Для проецирования точки А на плоскости проекций используются следующие её координаты:
П1 — А′(x, y)
П2 — А′′(x, z)
П3 — А′′′(y, z)
См. также[править | править код]
- Эпюра
Примечания[править | править код]
- ↑ Monge G. Géométrie descriptive. — Paris, 1799. — 132 p.
Литература[править | править код]
- Краткий справочник по начертательной геометрии и машиностроительному черчению / Н. П. Сберегаев, М. А. Герб. М. — Л., Машиностроение, 1965, 264с.
- Курс начертательной геометрии / В. О. Гордон, М. А. Семенцов-Огиевский. М.: Наука. 1971. 367с.
- Краткий курс начертательной геометрии / И. С. Альтшулер. Минск, Высшая школа, 1965. 271с.
- Начертательная геометрия / С. А. Фролов. — М.: Машиностроение, 1978 — 240с.
Источник

Запрос «Эпюр» перенаправляется сюда; см. также другие значения.
Не следует путать с Чертёж.
Не следует путать с Эпюра.
Эпю́р (фр. epure — чертёж) — чертёж, на котором пространственная фигура изображена методом нескольких (по ГОСТу трёх, но не всегда) плоскостей. Обычно оно даёт 3 вида: фронтальную, горизонтальную и профильную проекции (фасад, план, профиль). Чертёж проецируется на взаимно перпендикулярные, а затем развернутые на одну плоскости.
История
Сведения и приемы построений, обусловливаемые потребностью в плоских изображениях пространственных форм, накапливались постепенно еще с древних времен. В течение продолжительного периода плоские изображения выполнялись преимущественно как изображения наглядные. С развитием техники первостепенное значение приобрел вопрос о применении метода, обеспечивающего точность и удобоизмеримость изображений, то есть возможность точно установить место каждой точки изображения относительно других точек или плоскостей и путём простых приемов определить размеры отрезков линий и фигур.
Будучи одним из министров в революционном правительстве Франции, Гаспар Монж много сделал для её защиты от иностранной интервенции и для победы революционных войск. Начав с задачи точной резки камней по заданным эскизам применительно к архитектуре и фортификации, Монж пришёл к созданию методов, обобщённых им впоследствии в новой науке — начертательной геометрии, творцом которой он по праву считается. Учитывая возможность применения методов начертательной геометрии в военных целях при строительстве укреплений, руководство Мезьерской школы не допускало открытой публикации вплоть до 1799 года[1] (стенографическая запись лекций была сделана в 1795 году).
Система двух плоскостей проекции
рис.1 Система двух плоскостей проекций: а — расположение плоскостей проекций; б — совмещение плоскостей проекций
В данном случае, для построения изображения в двух плоскостях проекций, горизонтальная плоскость проекций П1 и фронтальная плоскость проекций П2 совмещаются в одну, как показано на рис.1. В пересечении они дают ось проекций x и делят пространство на четыре четверти (квадранта).
Система трех плоскостей проекций
рис.2 Система трех плоскостей проекций: а — расположение плоскостей проекций; б — совмещение плоскостей проекций
В системе трех плоскостей проекций совмещаются все три плоскости проекций (П1 — горизонтальная, П2 — фронтальная и П3 — профильная), как показано на рис.2. Плоскости образуют три оси проекций (оси координат) и восемь прямоугольных трехгранников, деля пространство на восемь октантов.
Для проецирования точки А на плоскости проекций используются следующие её координаты:
П1 — А′(x, y)
П2 — А′′(x, z)
П3 — А′′′(y, z)
См. также
- Эпюра
Примечания
- ↑ Monge G. Géométrie descriptive. — Paris, 1799. — 132 p.
Литература
- Краткий справочник по начертательной геометрии и машиностроительному черчению / Н. П. Сберегаев, М. А. Герб. М. — Л., Машиностроение, 1965, 264с.
- Курс начертательной геометрии / В. О. Гордон, М. А. Семенцов-Огиевский. М.: Наука. 1971. 367с.
- Краткий курс начертательной геометрии / И. С. Альтшулер. Минск, Высшая школа, 1965. 271с.
- Начертательная геометрия / С. А. Фролов. — М.: Машиностроение, 1978 — 240с.
![]()
Эта страница в последний раз была отредактирована 13 ноября 2018 в 17:02.
Источник
Построение эпюр продольных сил – это решение статически определимой задачи. Производится для выявления картины нагрузки упругого тела. Вернее, уточнения ее схематизации.
Необходимо для определения наиболее напряженного, так называемого «опасного» сечения. Затем методами сопромата (сопротивления материалов) проводится анализ с прогнозированием перемещений элементов конструкции.
Но всему свое время. Сначала немного о терминах.
Основные понятия
Брусом (балкой) называют тело, вытянутое вдоль оси. То есть длина преобладает над шириной и высотой.

Если имеются только осевые (продольные) силы, то объект подвергается растяжению/сжатию. В этом случае в материале возникают только нормальные поперечному сечению силы противодействия и тело считают стержнем.
Статическая определимость подразумевает достаточность схемы для установления внутренних усилий противодействия. Участок – часть балки с неизменным сечением и характерной нагрузкой.
Правила построения учитывают знаки усилий. Растягивающие принимают положительными, сжимающие – отрицательными.
В системе СИ силы измеряются в ньютонах (Н). Длины в метрах (м).
Что такое эпюра продольных сил
Показывает, какой силой (в нашем предположении нормальной) загружен каждый участок. По всей длине стержня. Иначе говоря, эпюра – наглядное графическое изображение изменения нагрузки по всей длине конструкции.
Как построить эпюру продольных сил
Используется метод сечений. Балка виртуально рассекается на каждом участке и ищется противодействующая N. Ведь задача статическая.
Сопротивление рассчитывается по формуле:
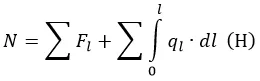
где:
Fl – действующие на участке l силы (Н);
ql – распределенные нагрузки (Н/м).
Порядок построения:
1. Рисуется схема балки и механизмов закрепления;
2. Производится разделение на участки;
3. Для каждого рассчитывается N с учетом знаков. Если у балки есть незакрепленный конец, то начинать удобнее именно с него. В противном случае считается реакция опор. И оптимальнее выбирать сечение с меньшим количеством действующих факторов:
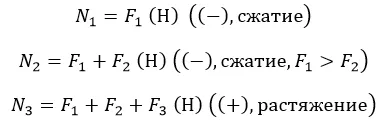
Нетрудно заметить, что последнее уравнение дает еще и реакцию опоры;
4. Параллельно оси стержня намечается база эпюры. Положительные значения масштабировано проставляются выше, отрицательные – ниже. Эпюру наглядно совмещать с расчетной схемой. Итоговый результат и промежуточные сечения показаны на рис. 1.
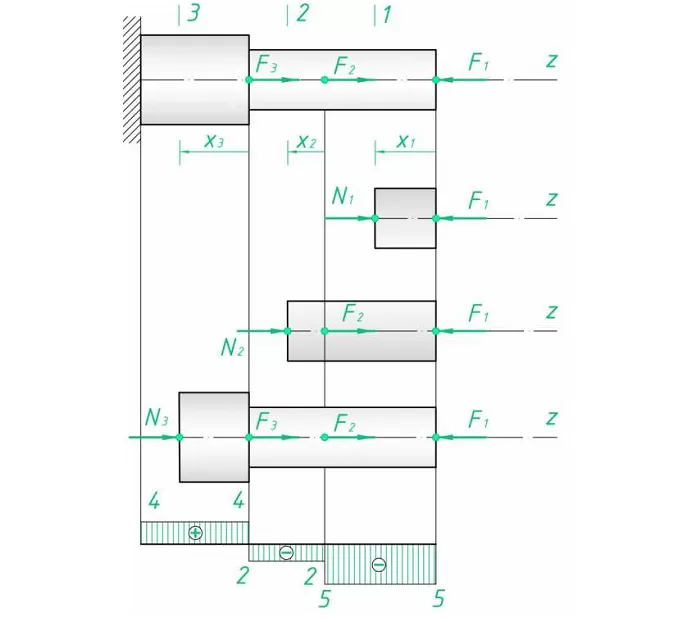
Рис. 1. Эпюра продольных сил
Рассмотрим случай:
F1 = 5 (кН);
F2 = 3 (кН);
F3 = 6 (кН).
Вычислим:
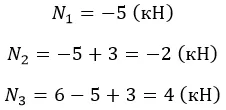
Проверить эпюру можно по скачкам: изменения происходят в точках приложения сил на их величину.
Пример построения эпюр и решения задач
Построить эпюру сил для следующего случая (рис. 2):
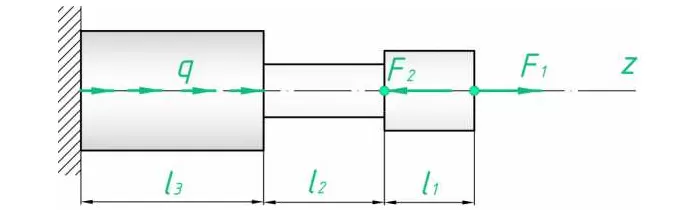
Рис. 2
Дано:
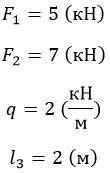
Решение.
Разбиение на участке вполне очевидно. Найдем сопротивление на выделенных:
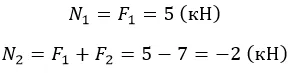
Распределенная нагрузка зависит от длины, на которой приложена. Поскольку нарастает линейно, значение N2 будет постепенно увеличиваться/уменьшаться в зависимости от знака q.
Эпюра такого вида усилия представляет собой прямоугольный треугольник с катетами l3 и ql3 (в масштабе). Поскольку распределение линейно.
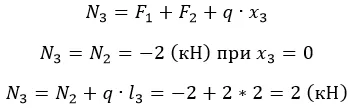
По полученным данным строим эпюру (рис. 3).
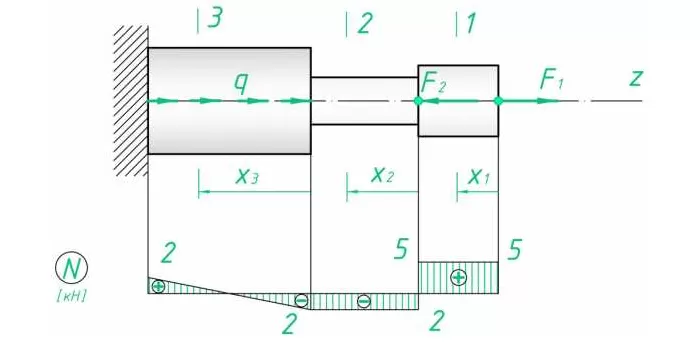
Рис. 3
Заключение
Приведенный алгоритм является предварительным этапом в расчете модели на прочность. «Слабое» место находится уже с учетом площади поперечного сечения.
В сети имеются онлайн сервисы для помощи в расчетах при вычерчивании. Но стоит ли ими пользоваться, если процедура настолько проста? Если не запутаться в знаках, конечно. Это самая распространенная ошибка.
Источник
Эпюрами поперечных сил и изгибающих моментов называют графические изображения функций Q и M по длине балки при изгибе.
Посмотреть подробные примеры построения эпюр >>
Эпюры строятся для визуального представления распределения внутренних силовых факторов и определения опасных (т.е. наиболее нагруженных) с точки зрения прочности участков бруса.
Рассмотрим некоторые примеры на построение эпюр в балках:
Эпюры при чистом изгибе
Для консольной балки: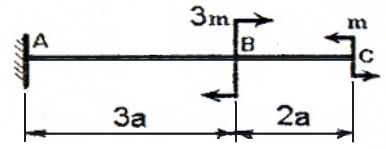
Рис. 1
имеем два силовых участка (AB и BC) и на каждом из них, применяя метод сечений, будем рассматривать, например правую от сечения часть, используя формулы и правило знаков для расчета внутренних силовых факторов.
Отсчет координаты z можно вести от единого начала координат или для каждого силового участка в отдельности.
I силовой участок (BC): 0 ≥ z1 ≥ 2a (рис. 2 а,г)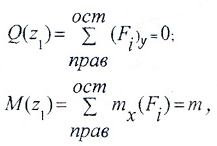
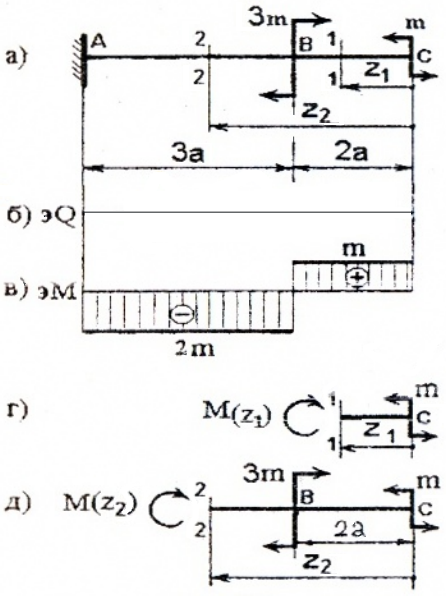
Рис. 2
т.е. Q(z1)=0 на всем участке, а M(z1)=m=const.
Ординаты эпюр Q и M со знаком плюс (+) будем откладывать вверх от нулевой (базовой) линии, при этом эпюру M будем строить на сжатых волокнах.
II силовой участок (AB): 2a ≥ z2 ≥ 5a (рис. 2 а,д)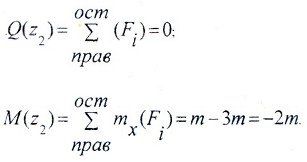
Откладывая на границах участков в сечениях C, B и A значения полученных ординат Q и M, строим эпюры (рис. 2 б, в).
Более нагруженным оказался участок AB, он и является опасным: Mmax=|2m|.
Так как поперечные силы Q по всей длине балки равны нулю, балка испытывает чистый изгиб.
Эпюры при поперечном изгибе
Построение эпюр Q и M для балки, изображенной на рис. 3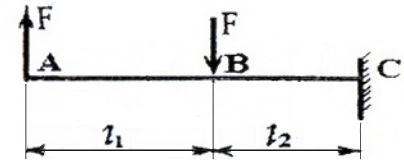
Рис. 3
проводим аналогично, но рассматривать будем левые от сечений части, т.к. в правые войдут реакции в заделке, что несколько усложняет вычисления.
I силовой участок (AB): 0 ≥ z1 ≥ l1 (рис. 4, а, г)
Q(z1)= F=const, на всем участке постоянная величина,
M(z1)=F×z1, уравнение прямой, график строим по двум граничным точкам:
M(z1=0)=F×0=0 – в сечении A;
M(z1=l1)=F× l1 — в сечении B.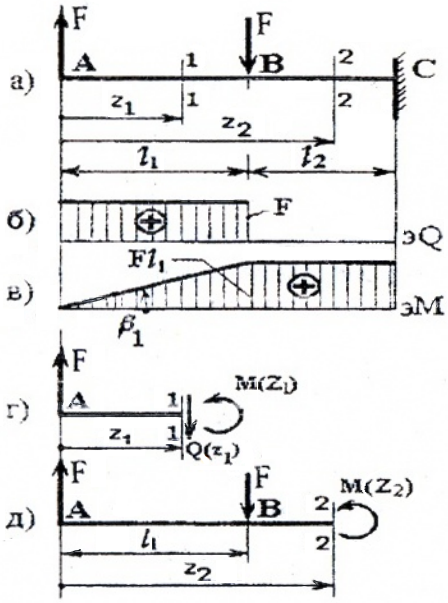
Рис. 4
II силовой участок (BC): l1 ≥ z2 ≥ (l1+ l2) (рис. 4, а, д)
Q(z2)= F-F=0;
M(z2)=F×z2— F×(z2— l1)=F ×l1=const.
Построив эпюры Q и M по всей длине балки (рис. 4 а, б, в), видим, что на первом участке — деформация прямого поперечного изгиба, т.к. Q≠0, M≠0; а на втором – прямого чистого изгиба.
Опасным является сечение B, в котором действуют Qmax=F, Mmax=Fl1.
Геометрическая проверка эпюр
Геометрическая проверка правильности построения эпюр Q и M по дифференциальным зависимостям заключается в следующем:
Для всех силовых участков находим: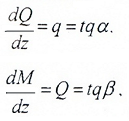
где α, β – углы наклона касательных к эпюрам Q и M относительно оси абсцисс (базовой линии).
На участке “AB” α1=0 (линия эпюры Q горизонтальна), следовательно,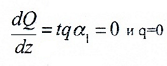
распределенная нагрузка отсутствует;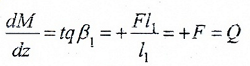
функция M (z1) – возрастающая.
На участке “BC”: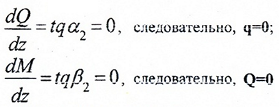
Так как все дифференциальные проверки выполняются, эпюры построены верно.
Эпюры для двухопорных балок
Рассматривая расчетные схемы такого типа, как двухопорная балка (рис. 5),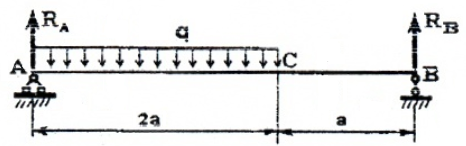
Рис. 5
необходимо вначале найти опорные реакции и только потом строить эпюры.
Определим реакции в обеих опорах, для этого используем два независимых уравнения статики, т.к. у нас плоская система параллельных сил.
Обычно, рекомендуется использовать суммы моментов вокруг опорных точек, например: ∑MA=0 и ∑MB=0.
Записываем уравнения и находим значения реакций: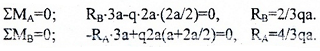
Чтобы убедиться в правильности полученных значений необходимо провести «арифметическую проверку» тождества по оставшемуся из зависимых уравнений: ∑FY=0 или ∑MС=0.
Проверим через сумму сил, приложенных к балке (включая найденные опорные реакции). Она должна равняться нулю (при округлении значений, может появиться погрешность).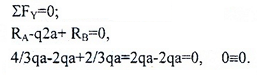
Для построения эпюр рассмотрим два силовых участка: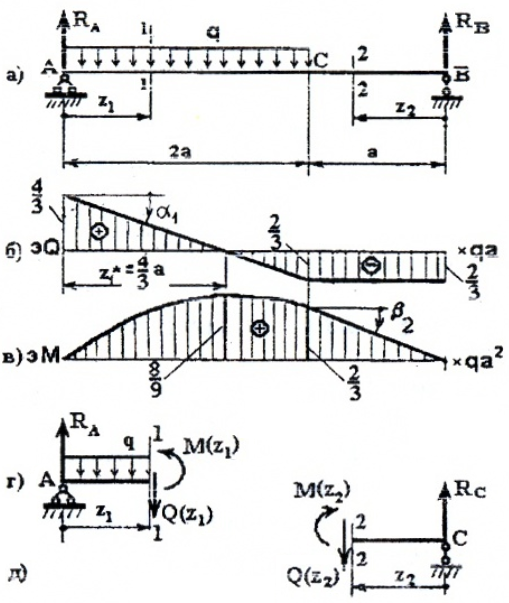
Рис. 6
I участок (AC): 0 ≥ z1 ≥2a (рис. 6, а, г)
Q(z1)=RA-qz1 — прямая, которую строим по двум граничным точкам: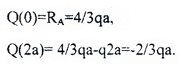
M(z1)=RAz1-qz1(z1/2)= RAz1-qz12/2 – парабола.
Строим эту кривую по трем точкам: по двум граничным (0 и 2a) и z*, которая соответствует Mmax(z*), и дифференциальной зависимости: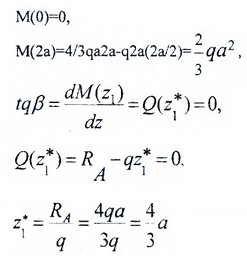
Определяем экстремум эпюры M на участке: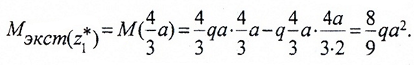
II участок (BC): 0 ≥ z2 ≥ a (рис. 6, а, д)
Q(z2)= -RB= -2/3qa;
M(z2)=RBz2,
M(z2=0)=0,
M(z2=a)=2/3qa2.
Выполним проверку дифференциальных зависимостей.
I силовой участок: 0 ≥ z1 ≥ 2a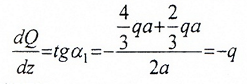
— направлена вниз, функция Q(z1) – убывающая.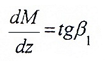
— проверка визуально: чем больше угол наклона β1, тем больше значение Q(z1).
II силовой участок: 0 ≥ z2 ≥ a.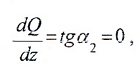
следовательно, q=0.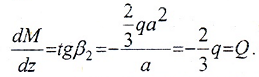
функция M(z) – убывающая.
Все проверки выполнены, следовательно, эпюры построены верно.
По эпюрам видно, что опасных сечений два (рис. 6):
По моменту при z1*=4/3a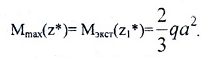
По силе в сечении «A»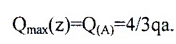
После построения и проверки эпюр можно приступать к расчетам балки на прочность и жесткость.
Подробные примеры построения эпюр >
Лекции по сопромату >
Примеры решения задач >
Источник
История
Сведения и приемы построений, обусловливаемые потребностью в плоских изображениях пространственных форм, накапливались постепенно еще с древних времен. В течение продолжительного периода плоские изображения выполнялись преимущественно как изображения наглядные. С развитием техники первостепенное значение приобрел вопрос о применении метода, обеспечивающего точность и удобоизмеримость изображений, т. е. возможность точно установить место каждой точки изображения относительно других точек или плоскостей и путем простых приемов определить размеры отрезков линий и фигур.
Будучи одним из министров в революционном правительстве Франции, Гаспар Монж много сделал для её защиты от иностранной интервенции и для победы революционных войск. Начав с задачи точной резки камней по заданным эскизам применительно к архитектуре и фортификации, Монж пришёл к созданию методов, обобщённых им впоследствии в новой науке — начертательной геометрии, творцом которой он по праву считается. Учитывая возможность применения методов начертательной геометрии в военных целях при строительстве укреплений, руководство Мезьерской школы не допускало открытой публикации вплоть до 1799 года[1] (стенографическая запись лекций была сделана в 1795 году).
Система двух плоскостей проекции
![]()
рис.1 Система двух плоскостей проекций: а – расположение плоскостей проекций; б – совмещение плоскостей проекций
В данном случае, для построения изображения в двух плоскостях проекций, горизонтальная плоскость проекций П1 и фронтальная плоскость проекций П2 совмещаются в одну, как показано на рис.1. В пересечении они дают ось проекций x и делят пространство на четыре четверти (квадранта).
Система трех плоскостей проекций
![]()
рис.2 Система трех плоскостей проекций: а – расположение плоскостей проекций; б – совмещение плоскостей проекций
В системе трех плоскостей проекций совмещаются все три плоскости проекций (П1 – горизонтальная, П2 – фронтальная и П3 – профильная), как показано на рис.2. Плоскости образуют три оси проекций (оси координат) и восемь прямоугольных трехгранников, деля пространство на восемь октантов. Для проецирования точки А на плоскости проекций используются следующие ее координаты: П1 – А′(x, y) П2 – А′′(x, z) П3 – А′′′(y, z)
См. также
- Эпюра
Примечания
- ↑ Monge G. Géométrie descriptive. — Paris, 1799. — 132 p.
Литература
- Краткий справочник по начертательной геометрии и машиностроительному черчению / Н.П. Сберегаев, М.А. Герб. М. – Л., Машиностроение, 1965, 264с.
- Курс начертательной геометрии / В.О. Гордон, М.А. Семенцов-Огиевский. М.: Наука. 1971. 367с.
- Краткий курс начертательной геометрии / И.С. Альтшулер. Минск, Высшая школа, 1965. 271с.
- Начертательная геометрия / С.А. Фролов. – М.: Машиностроение, 1978 – 240с.
Wikimedia Foundation.
2010.
Синонимы:
Смотреть что такое “Эпюр” в других словарях:
эпюр — эпюра, чертеж Словарь русских синонимов. эпюр сущ., кол во синонимов: 2 • чертеж (14) • эпюра … Словарь синонимов
ЭПЮР — (эпюра) (от франц. epure чертеж) чертеж, на котором пространственная фигура изображена методом двух (или трех) ортогональных проекций на взаимно перпендикулярные, а затем развернутые плоскости … Большой Энциклопедический словарь
эпюр — а, м., ЭПЮРА ы, ж épure f. 1. спец. Чертеж проекций фигуры, полученный путем совмещения плоскостей проекций. БАС 1. О нем <профессоре> говорили, будто он вымерял циркулем фигуру своей жены и по эпюрам скроил ей бальное платье, которое… … Исторический словарь галлицизмов русского языка
эпюр — эпюр, м. и устарелое эпюра, ж … Словарь трудностей произношения и ударения в современном русском языке
ЭПЮР — (эпюра) (1) чертёж пространственной фигуры, которая изображена методом её ортогональных проекций на две взаимно перпендикулярные плоскости горизонтальную и вертикальную, с последующим совмещением этих плоскостей путём поворота одной из них вокруг … Большая политехническая энциклопедия
эпюр — (фр. eрurе чертеж) эпюра 1) чертеж, на котором пространственная фигура изображена методом ортогональных проекций на три плоскости; 2) графическое изображение закона изменения нек рой величины в зависимости от другой величины. Новый словарь… … Словарь иностранных слов русского языка
эпюр — эпюра (от франц. épure чертёж), чертёж, на котором пространственная фигура изображена методом двух (или трёх) ортогональных проекций на взаимно перпендикулярные, а затем развёрнутые плоскости. * * * ЭПЮР ЭПЮР (эпюра) (от франц. epure чертеж),… … Энциклопедический словарь
Эпюр — или эпюра (от франц. épure чертёж), чертёж, на котором пространственная фигура изображена методом ортогональных проекций, т. е. комплексный чертёж (см. Начертательная геометрия) … Большая советская энциклопедия
Эпюр — м. 1. Чертеж проекций фигуры, полученный путём совмещения плоскостей проекций. 2. Графическое изображение закономерного изменения некоторой величины в зависимости от изменения другой величины. Толковый словарь Ефремовой. Т. Ф. Ефремова. 2000 … Современный толковый словарь русского языка Ефремовой
эпюр — эпюр, эпюры, эпюра, эпюров, эпюру, эпюрам, эпюр, эпюры, эпюром, эпюрами, эпюре, эпюрах (Источник: «Полная акцентуированная парадигма по А. А. Зализняку») … Формы слов
Книги
- Сопротивление материалов: построение эпюр внутренних силовых факторов, изгиб. Учебное пособие для академического бакалавриата, Асадулина Е.Ю.. Учебное пособие включает в себя методику определения внетренних силовых факторов и постоение их эпюр, вопросы по пределеню геометрических характеристик поперечных сечений бруса, необходимых… Подробнее Купить за 551 грн (только Украина)
- Сопротивление материалов: построение эпюр внутренних силовых факторов, изгиб. Учебное пособие для академического бакалавриата, Асадулина Е.. Учебное пособие включает в себя методику определения внетренних силовых факторов и постоение их эпюр, вопросы по пределеню геометрических характеристик поперечных сечений бруса, необходимых… Подробнее Купить за 459 грн (только Украина)
- Сопротивление материалов: построение эпюр внутренних силовых факторов, изгиб. Учебное пособие для академического бакалавриата, Асадулина Е.. Учебное пособие включает в себя методику определения внетренних силовых факторов и постоение их эпюр, вопросы по пределеню геометрических характеристик поперечных сечений бруса, необходимых… Подробнее Купить за 355 руб
Другие книги по запросу «Эпюр» >>
Источник
