Какими свойствами обладает электронный газ в состоянии вырождения
Вырожденный газ — газ, на свойства которого существенно влияют квантовомеханические эффекты, возникающие вследствие тождественности его частиц. Вырождение наступает в условиях, когда расстояния между частицами газа становятся соизмеримыми с длиной волны де Бройля; в зависимости от спина частиц выделяются два типа вырожденных газов — ферми-газ, образованный фермионами (частицами с полуцелым спином) и бозе-газ, образованный бозонами (частицами с целым спином).
Условия вырождения[править | править код]
Влияние тождественности частиц становится существенным при уменьшении средних расстояний между ними до расстояний, соизмеримых с длиной волны де Бройля, ассоциированной с частицей, то есть выполняется условие:
где — объемная концентрация частиц,
— длина волны де Бройля частиц массы , движущихся со скоростью .
Условия вырождения выполняются при достаточно низкой температуре (для идеального газа ) и высокой концентрации частиц .
Вырождение Ферми- и Бозе-газов[править | править код]
Зависимость давления вырожденного ферми-газа от температуры, сохранению состояния вырождения соответствует горизонтальная ветвь.
Тип вырождения различен для частиц с полуцелым спином (фермионов, статистика Ферми — Дирака) и частиц с целым спином (бозонов, статистика Бозе — Эйнштейна), соответственно различаются и свойства ферми- и бозе-газов.
Если для Ферми-газа вследствие действия принципа Паули давление вырожденного газа выше давления идеального газа в тех же условиях, то для вырожденного Бозе-газа давление ниже давления идеального газа вследствие конденсации Бозе — Эйнштейна.
У ферми-газа (к которому относится электронный газ в металле) при полном вырождении (при ) заполнены все нижние энергетические уровни вплоть до некоторого максимального, называемого уровнем Ферми, а все последующие остаются пустыми. Повышение температуры лишь незначительно изменяет такое распределение электронов металла по уровням: малая доля электронов, находящихся на уровнях, близких к уровню Ферми, переходит на пустые уровни с большей энергией, освобождая таким образом уровни ниже фермиевского, с которых был совершен переход.
При вырождении газа бозонов из частиц с отличной от нуля массой (такими бозонами могут быть атомы и молекулы) некоторая доля частиц системы должна переходить в состояние с нулевым импульсом; это явление называется Бозе — Эйнштейновской конденсацией. Чем ближе температура к абсолютному нулю, тем больше частиц должно оказаться в этом состоянии. Однако, системы таких частиц при понижении температуры до очень низких значений переходят в твёрдое или жидкое (для гелия) состояния, к которым неприменимо приближение идеального газа.
Для газа из бозонов нулевой массы, к которым относятся фотоны, температура вырождения равна бесконечности; поэтому фотонный газ всегда вырожденный, и классическая статистика к нему не применима. Фотонный газ является единственным вырожденным идеальным бозе-газом стабильных частиц. Однако Бозе-Эйнштейновской конденсации в нём не происходит, так как не существует фотонов с нулевым импульсом (фотоны всегда движутся со скоростью света).
Явление вырождения Ферми-газов играет важную роль в эволюции звёзд: так, давление электронного вырожденного газа уравновешивает тяготение в белых карликах, а давление нейтронного вырожденного газа уравновешивает тяготение в нейтронных звёздах.
См. также[править | править код]
- Квантовый газ#Вырожденный газ
- Вырождение (квантовая механика)
- Идеальный газ
- Уравнение Саха-Ленгмюра
Ссылки[править | править код]
- Астронет — Вырожденный газ
- Астрогалактика — Вырожденное состояние вещества
Источник

Вырожденный газ в недрах звезды
В отличие от идеального газа, представляющего собой математическую модель, на свойства вырожденного газа существенно влияют квантовомеханические эффекты. В большей мере эти эффекты вызваны тождественностью частиц согласно квантовой механике.
Температура вырождения
Газ начинает вырождаться при понижении температуры до так называемой температуры вырождения. Полное вырождение соответствует температуре равной абсолютному нулю. Квантовомеханические эффекты проявляются тем существеннее, чем меньше расстояние между частицами. Дело в том, что классическая механика работает при условии, что расстояние между частицами значительно превышает длину волны де Бройля, с уменьшением же расстояния начинает проявляться волновая природа частицы.
Известно, что чем больше скорость частиц в газе, тем выше температура. Из этого следует, что температура вырождения тем выше, чем больше плотность газа (меньшее расстояние между частицами) и чем меньше масса его частиц. Например, так как масса электрона относительно мала (около 10-27 г), а плотность электронов в металле высока (1022 на 1 см3), то вырожденный электронный газ в металлах можно наблюдать при температуре не меньше 10 000 кельвин.
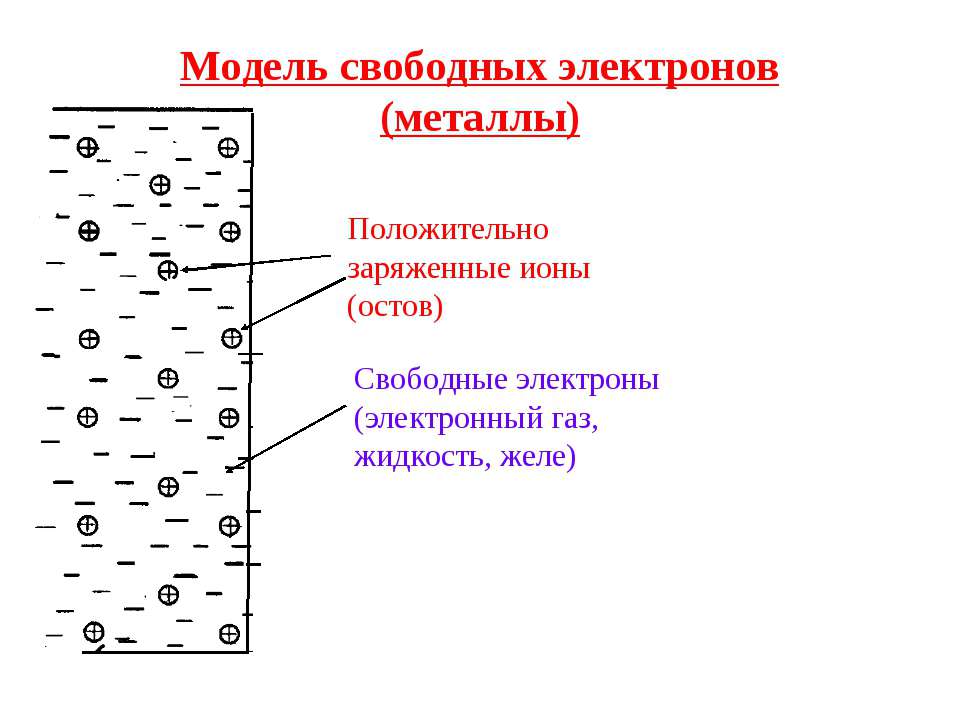
Электронный газ в металле
В отличие от электронного газа, температуры вырождения обычных молекулярных и атомных газов близки к температуре абсолютного нуля. Потому такой газ обычно подчиняется классической механике. Газ с высокой степенью вырождения является квантовым газом.
Принцип тождественности
Говоря о принципе тождественности частиц – это одно из основных различий между квантовой и классической механикой. Его суть состоит в том, что в классической механике всегда можно проследить за траекторией тела, а потому и явно отличить одно тело от другого с течением времени. В случае же с квантовым миром, наблюдение одной частицы невозможно, так как она не имеет определенной траектории, а распространяется в соответствии с волнами де Бройля. Это волны вероятности, которые определяют вероятность обнаружения частицы в заданной точке пространства.
Таким образом, если нельзя отследить траекторию некоторой частицы, то нельзя и утверждать, что с течением времени мы наблюдаем одну и ту же частицу, а не другую частицу того же сорта.

Область возможного обнаружения электрона вокруг ядра
Материалы по теме
Плотность вероятности обнаружения частицы в том или ином месте описывается при помощи волновой функции (а вернее квадрату ее модуля). Так как природа бозонов и фермионов отличается, то и их волновые функции ведут себя по-разному. По этой причине вырожденный газ разделяют на газ, состоящий из частиц с целым спином – бозонов (вырожденный Бозе-газ), и состоящий из частиц с полуцелым спином – фермионов (Ферми газ).
Вырожденный газ в природе
Электронный вырожденный газ обычно встречается в белых карликах, образуя ядро звезды, в результате сильного давления со стороны ее верхних слоев. Так как электроны – это фермионы, то они подчиняются принципу Паули – несколько фермионов не могут находиться в одном состоянии (в т. ч. в одной точке). По этой причине внешние слои звезды способны сжать электронный газ лишь до определенного объема.
В случае коллапса звезды – она превращается в нейтронную. В таком случае, под давлением верхних слоев атмосферы электроны «сливаются» с протонами, вследствие чего превращаются в нейтральные частицы – нейтроны. Далее нейтроны сжимаются массой звезды до высокой степени вырождения, образуя нейтронный вырожденный газ.
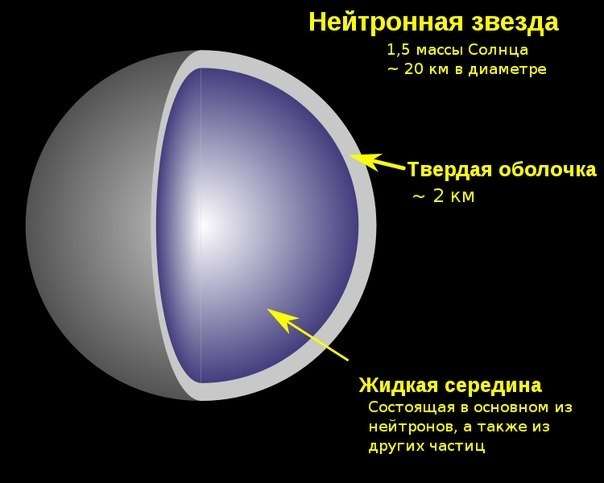
Строение нейтронной звезды
Источник
Важное принципиальное значение имеет изучение свойств ферми-газа при достаточно низких температурах. Как мы увидим ниже, температуры, о которых при этом идет речь, фактически могут еще быть, с других точек зрения, весьма высокими.
Имея в виду наиболее важные применения статистики Ферми, будем говорить ниже об электронном газе; соответственно этому полагаем (спин s = 1 /2).
Начнем с рассмотрения электронного газа при абсолютном нуле температуры (полностью вырожденный ферми-газ). В таком газе электроны будут распределены по различным квантовым состояниям таким образом, чтобы полная энергия газа имела наименьшее возможное значение. Поскольку в каждом квантовом состоянии может находиться не более одного электрона, то электроны заполнят все состояния с энергиями от наименьшей (равной нулю) до некоторой наибольшей, величина которой определяется числом электронов в газе.
С учетом двукратного ) спинового вырождения уровней, число квантовых состояний электрона, движущегося в объеме V с абсолютной величиной импульса в интервале между равно
Электроны заполняют все состояния с импульсами от нуля до граничного значения , об этом значении говорят как о радиусе ферми-сферы в импульсном пространстве. Полное число электронов в этих состояниях
откуда для граничного импульса имеем
и для граничной энергии
Эта энергия имеет простой термодинамический смысл. В согласии со сказанным выше функция распределения Ферми по квантовым состояниям (с определенными значениями импульса и проекции спина)
в пределе обращается в «ступенчатую» функцию: единица при и нуль при (на рис. 6 эта функция изображена сплошной линией). Отсюда видно, что химический потенциал газа при Т = 0 совпадает с граничной энергией электронов:
Полная энергия газа получится умножением числа состояний (57,1) на и интегрированием по всем импульсам:
или, подставив (57,2):
Рис. 6.
По общему соотношению (56,8) находим, наконец, уравнение состояния газа
Таким образом, давление ферми-газа при абсолютном нуле температуры пропорционально его плотности в степени 5/3.
Полученные формулы (57,6-7) применимы приближенно также и при температурах, достаточно близких (при данной плотности газа) к абсолютному нулю. Условие их применимости (условие «сильного вырождения» газа) требует, очевидно, малости Т по сравнению с граничной энергией
Это условие, как и следовало ожидать, противоположно условию (45,6) применимости статистики Больцмана. Температуру называют температурой вырождения.
Вырожденный электронный газ обладает своеобразной особенностью он становится тем более идеальным, чем больше его плотность. В этом легко убедиться следующим образом.
Рассмотрим плазму — газ, состоящий из электронов и соответствующего количества положительно заряженных ядер, компенсирующих заряд электронов (газ из одних только электронов был бы, очевидно, вообще неустойчивым; выше мы не говорили о ядрах, поскольку вследствие предполагающейся идеальности наличие ядер не сказывается на термодинамических величинах электронного газа). Энергия кулонового взаимодействия электронов с ядрами (отнесенная к одному электрону) порядка величины где – заряд ядра, — среднее расстояние между электронами и ядрами. Условие идеальности газа заключается в требовании малости этой энергии по сравнению со средней кинетической энергией электронов, которая по порядку величины совпадает с граничной энергией . Неравенство
после подстановки и выражения (57,3) для дает условие
Мы видим, что это условие выполняется тем лучше, чем больше плотность газа
Задача
Определить число столкновений со стенкой в электронном газе при абсолютном нуле температуры.
Решение. Число электронов (в единице объема) с импульсами в интервале направленными под углом к нормали к стенке в интервале , есть
Искомое число столкновений v (отнесенное к стенки) получается умножением на и интегрированием по в пределах от 0 до и по до . В результате найдем
Источник
Вырожденный газ, газ, свойства которого существенно отличаются от свойств классического идеального газа вследствие квантовомеханического влияния одинаковых частиц друг на друга. Это взаимное влияние частиц обусловлено не силовыми взаимодействиями, отсутствующими у идеального газа, а тождественностью (неразличимостью) одинаковых частиц в квантовой механике (см. Тождественности принцип). В результате такого влияния заполнение частицами возможных уровней энергии даже в идеальном газе зависит от наличия на данном уровне других частиц. Поэтому теплоёмкость и давление такого газа иначе зависят от температуры, чем у идеального классического газа; по-другому выражается энтропия, свободная энергия и т. д.
Вырождение газа наступает при понижении его температуры до некоторого значения, называемого температурой вырождения. Полное вырождение соответствует абсолютному нулю температуры.
Влияние тождественности частиц сказывается тем существеннее, чем меньше среднее расстояние между частицами r по сравнению с длиной волны де Бройля частиц l = h/mv (m — масса частицы, v — её скорость, h — Планка постоянная). Это объясняется тем, что классическая механика применима к движению частиц газа лишь при условии r >> l. Так как скорость частиц газа связана с температурой (чем больше скорость, тем выше температура), то температура вырождения, определяющая границу применимости классической теории, тем выше, чем меньше масса частиц газа и чем больше его плотность (т. е. чем меньше среднее расстояние между частицами). Поэтому температура вырождения особенно велика (порядка 10 000 К) для электронного газа в металлах: масса электронов очень мала (~ 10-27г), а их плотность в металлах очень велика (1022 электронов в 1 см3). Электронный газ в металлах вырожден при всех температурах, при которых металл остаётся в твёрдом состоянии.
Для обычных атомных и молекулярных газов температура вырождения близка к абсолютному нулю, так что такой газ практически всегда ведёт себя как классический (при таких низких температурах все вещества находятся в твёрдом состоянии, кроме гелия, являющегося квантовой жидкостью при сколь угодно близких к абсолютному нулю температурах).
Поскольку характер несилового влияния тождественных частиц друг на друга различен для частиц с целым (бозоны) и полуцелым (фермионы) спином, то поведение газа из фермионов (ферми-газа) и из бозонов (бозе-газа) также будет различным при вырождении.
У ферми-газа (к которому относится электронный газ в металле) при полном вырождении (при Т = 0 К) заполнены все нижние энергетические уровни вплоть до некоторого максимального, называемого уровнем Ферми, а все последующие остаются пустыми. Повышение температуры лишь незначительно изменяет такое распределение электронов металла по уровням: малая доля электронов, находящихся на уровнях, близких к уровню Ферми, переходит на пустые уровни с большей энергией, освобождая таким образом уровни ниже фермиевского, с которых был совершен переход.
При вырождении газа бозонов из частиц с отличной от нуля массой (такими бозонами могут быть атомы и молекулы) некоторая доля частиц системы должна переходить в состояние с нулевым импульсом; это явление называется Бозе — Эйнштейна конденсацией. Чем ближе температура к абсолютному нулю, тем больше частиц должно оказаться в этом состоянии. Однако, как уже говорилось, системы таких частиц при понижении температуры до очень низких значений переходят в твёрдое или жидкое (для гелия) состояния, в которых значительны силовые взаимодействия между частицами и к которым поэтому неприменимо приближение идеального газа. Явление Бозе — Эйнштейна конденсации в жидком гелии, который можно рассматривать как неидеальный газ из так называемых квазичастиц, приводит к появлению сверхтекучести.
Для газа из бозонов нулевой массы, к которым относятся фотоны (спин 1), температура вырождения равна бесконечности; поэтому фотонный газ — всегда вырожденный и классическая статистика к нему не применима ни при каких условиях. Фотонный газ является единственным вырожденным идеальным бозе-газом стабильных частиц. Однако Бозе — Эйнштейна конденсации в нём не происходит, так как не существует фотонов с нулевым импульсом (фотоны всегда движутся со скоростью света). При нулевой абсолютной температуре фотонный газ перестаёт существовать.
См. также Статистическая физика, Металлы, Полупроводники и лит. при этих статьях.
Г. Я. Мякишев.
Оглавление
Источник
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 января 2015;
проверки требуют 26 правок.
Квантовый газ — газ частиц или квазичастиц, подчиняющийся квантовой статистике.
Свойства квантового газа зависят от степени его вырождения, характеризующегося температурой вырождения. Температура вырождения зависит от плотности газа, , — концентрация частиц, — масса частицы, — постоянная Больцмана. При условии газ является невырожденным и распределение частиц по энергиям описывается распределением Больцмана. В случае газ попадает в область квантового вырождения и представляет собой, в зависимости от статистики частиц, вырожденный Ферми-газ (статистика Ферми — Дирака) или Бозе-газ (статистика Бозе — Эйнштейна).
Модель квантового газа широко применяется для решения задач физики твердого тела (электронный газ в металлах), астрофизики (свойства белых карликов и нейтронных звезд), физики конденсированного состояния (сверхтекучесть).
Различают идеальный и реальный квантовый газ.
Идеальный квантовый газ[править | править код]
Условием идеальности квантового газа является условие невзаимодействия между собой частиц, из которого он состоит. Благодаря отсутствию взаимодействия можно считать, что заполнение того или иного квантового состояния системы не влияет на заполнение других состояний. В общем случае, если между частицами есть, например, кулоновское взаимодействие, то, чтобы приближение идеального газа давало хорошие результаты, необходимо считать его слабым. Это приводит к условию разрежённости , где — длина рассеяния частиц или, что то же самое, . Следовательно, полагаться, что при , где — температура вырождения, свойства квантового газа во многом не зависят от статистики составляющих его частиц и могут описываться статистикой Максвелла — Больцмана. Также, так как нет возможности точно регулировать число частиц в системе, имеет смысл работать в терминах большого канонического ансамбля.
Тогда, в силу независимости состояний, статсумма идеального Бозе-Ферми газа задаётся формулой где — статсумма одноуровневой системы, суммирование происходит по всем уровням системы, верхние знаки соответствуют случаю Ферми-, нижние — Бозе-газа, — одночастичный гамильтониан, — химический потенциал газа.
Соответствующий этой статсумме большой термодинамический потенциал идеального квантового газа:
,
где — объём системы, — постоянная Планка, — вырождение по спину.
Среднее число частиц на уровне: .
Можно ещё больше унифицировать выражение для термодинамического потенциала, если заметить, что подынтегральная функция в случаях Ферми- и Бозе-газа отличается только знаком. Далее следует вынести из под интеграла все размерные параметры. Тогда термодинамический потенциал запишется в виде:
,
где была введена функция
,
С обозначениями:
Тогда, используя простое соотношение и термодинамические соотношения Максвелла , можно получить различные термодинамические характеристики в общем виде:
Эти формулы продолжают работать и при низких, и при высоких температурах.[прояснить]
Вырожденный газ[править | править код]
Вырожденный газ — газ, на свойства которого существенно влияют квантовомеханические эффекты, возникающие вследствие тождественности его частиц. Влияние тождественности частиц становится существенным при уменьшении средних расстояний между ними до расстояний, соизмеримых с длиной волны де Бройля, ассоциированной с частицей, то есть выполняется условие:
где — объемная концентрация частиц,
— длина волны де Бройля частиц массы , движущихся со скоростью .
Условия вырождения выполняются при достаточно низкой температуре (для идеального газа ) и высокой концентрации частиц .
Вырождение Ферми- и Бозе-газов[править | править код]
Зависимость давления вырожденного ферми-газа от температуры, сохранению состояния вырождения соответствует горизонтальная ветвь.
Свойства Бозе- и Ферми-газа принципиально различны: сколь угодно большое количество бозонов может находиться в одном квантовом состоянии, в то время как на одном квантовом состоянии может находиться не более одного фермиона.
Тип вырождения зависит от статистики, которой подчиняются частицы. Если для Ферми-газа вследствие действия принципа Паули давление вырожденного газа выше давления идеального газа в тех же условиях, то для вырожденного Бозе-газа давление ниже давления идеального газа вследствие конденсации Бозе — Эйнштейна.
У ферми-газа при полном вырождении (при ) заполнены все нижние энергетические уровни вплоть до некоторого максимального, называемого уровнем Ферми, а все последующие остаются пустыми. Повышение температуры лишь незначительно изменяет такое распределение электронов металла по уровням: малая доля электронов, находящихся на уровнях, близких к уровню Ферми, переходит на пустые уровни с большей энергией, освобождая таким образом уровни ниже фермиевского, с которых был совершен переход.
При вырождении газа бозонов из частиц с отличной от нуля массой (такими бозонами могут быть атомы и молекулы) некоторая доля частиц системы должна переходить в состояние с нулевым импульсом; это явление называется Бозе — Эйнштейновской конденсацией. Чем ближе температура к абсолютному нулю, тем больше частиц должно оказаться в этом состоянии. Однако, системы таких частиц при понижении температуры до очень низких значений переходят в твёрдое или жидкое (для гелия) состояния, к которым неприменимо приближение идеального газа.
Для газа из бозонов нулевой массы, к которым относятся фотоны, температура вырождения равна бесконечности; поэтому фотонный газ всегда вырожденный, и классическая статистика к нему не применима. Фотонный газ является единственным вырожденным идеальным бозе-газом стабильных частиц. Однако Бозе-Эйнштейновской конденсации в нём не происходит, так как не существует фотонов с нулевым импульсом (фотоны всегда движутся со скоростью света).
Важным примером Ферми-газа при достаточно низких температурах является электронный газ в металлах. Для этого газа температура вырождения оказывается порядка 10 000 К, следовательно, в металлах при комнатной температуре приближение вырожденного электронного газа работает хорошо. Стоит отметить, что в случае полупроводников данная модель переходит в модель Максвелла-Больцмана, благодаря расположению уровня Ферми внутри запрещенной зоны.
Явление вырождения Ферми-газов играет важную роль в эволюции звёзд: так, давление электронного вырожденного газа уравновешивает тяготение в белых карликах, а давление нейтронного вырожденного газа уравновешивает тяготение в нейтронных звёздах.
Ниже приведены основные формулы для обоих случаев вырождения.
Вырожденный Ферми-газ[править | править код]
При подынтегральное выражение в формуле для функции теряет непрерывность. Скачок функции происходит при энергии, равной — энергии Ферми. Когда температура близка, но отлична от нуля, подынтегральное выражение можно разложить в ряд (по параметру ) и интеграл принимает вид:
Подставляя это выражение в уравнения состояния и выражения для термодинамических характеристик, получаем ():
Решая первое уравнение методом итераций находим выражение для химического потенциала и энергии Ферми:
Таким образом, при близкой к нулю температуре, идеальный Ферми-газ находится в основном состоянии, его частицы занимают все уровни энергии вплоть до , а все уровни выше свободны.
Необходимо отметить, что приближение идеального газа не описывает множество важных эффектов, таких как явление сверхпроводимости, сверхтекучести и т. д.
Вырожденный Бозе-газ[править | править код]
При понижении температуры или увеличении плотности Бозе-газа параметр , следовательно химический потенциал и обратится в нуль при конечных значениях , связанных соотношением . При этом заселенность нулевого уровня формально равно бесконечности, поэтому точка называется точкой Бозе-конденсации. Явление Бозе-конденсации невозможно описать в рамках приближения идеального Бозе-газа, поэтому ограничимся описанием поведения Бозе-газа в окрестности точки Бозе-конденсации.
Асимптотикой функции при является
откуда при следует выражение для химического потенциала: где — отклонения от точки Бозе-конденсации.
Для расчёта энтропии и теплоёмкости также понадобятся асимптотики функций и , которые могут быть получены аналогично предыдущей и имеют вид:
См. также[править | править код]
- Уровень Ферми
- Конденсат Бозе — Эйнштейна
- Сверхпроводимость
- Сверхтекучесть
- Уравнение Саха-Ленгмюра
- Идеальный газ
- Вырождение (квантовая механика)
Литература[править | править код]
- Ландау Л. Д., Лифшиц Е. М. Статистическая физика.
- Куни Ф. М. Статистическая физика.
- М. Комарова, М. Налимов. Квантовые газы. — СПбГУ, 2005.
- Jean Letessier, Johann Rafelski, T. Ericson, P. Y. Landshoff. Hadrons and Quark-Gluon Plasma. — Cambridge University Press, 2002. — 415 p. — ISBN 9780511037276.
Источник
