Какими свойствами обладает функция y x 2
Тип урока:
- урок овладения знаниями и умениями при
построении и исследовании функции.
Учебник:
- Макарычев Ю. Н., Миндюк Н. Р. Математика. 7 класс
Цели:
построении графиков,
ответственность.
I. Опрос учащихся
- Что называется функцией?
- Что называется областью определения функции?
- Что называется областью значений функции?
- С какими функциями мы с вами познакомились?
- Что представляет из себя график линейной
функции? (прямая). Сколько точек необходимо
для построения данного графика?
(Функцией называется зависимость одной
переменной от другой, при которой каждому
значению независимой переменной соответствует
единственное значение зависимой переменной)
(Все значения, которые принимает независимая
переменная (аргумент), .образуют область
определения функции)
(Все значения, которые принимает зависимая
переменная, называются значениями функции)
а) с линейной функцией вида у = кх + b,
прямой пропорциональностью вида у = кх
б) с функциями вида у = х2 , у = х3
II.
Не выполняя построения, определите взаимное
расположение графиков функций, заданных
следующими формулами:
а) у = Зх + 2; у = 1,2х + 5;
b) y = 1,5х + 4; у = -0,2х + 4; у = х + 4;
с) у = 2х + 5; у = 2х – 7; у = 2х

Рисунок 1
На рисунке изображены графики линейных функций
(каждому ученику на парту выдается листок с
построенными графиками). Напишите формулу для
каждого графика
С графиками каких функций мы с вами ещё знакомы?
(у = х2; у = х3)
- Что является графиком функции у = х2
(парабола). - Сколько точек нам необходимо построить для
изображения параболы? (7, одна из которых
является вершиной параболы).
Давайте построим параболу, заданную формулой у
= х2
| x | -3 | -2 | -1 | 1 | 2 | 3 | |
| у = х2 | 9 | 4 | 1 | 1 | 4 | 9 | |
| у = х2 + 2 | 11 | 6 | 3 | 2 | 3 | 6 | 11 |
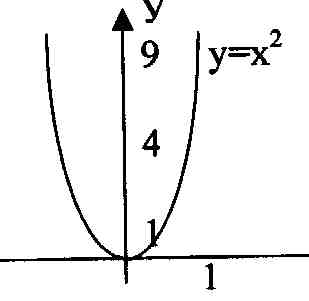
Рисунок 2
Какими свойствами обладает график функции у
= х3 ?
- Если х = 0, то у = 0 – вершина
параболы (0;0) - Область определения: х – любое число, Д(у)
= (- ?; ?) Д(у) = R - Область значений у ? 0
- E(y) = [0; ?) (квадратные скобки
говорят о непрерывности функции, об этом мы будем
говорить в старших классах). - (-х)2 = х
- Функция убывает на промежутке (-?; 0]
- Функция возрастает на промежутке [0; ?)
2 – функция четная. График
симметричен относительно оси у, т.е.
прямой х = 0.
Как вы думаете, как будет расположен график
функции у = х2 + 2? Давайте его
построим (заполнить таблицу значений).
Ребята, посмотрите по таблице, какие координаты
меняются.
Давайте исследуем график функции у = х + 2
а) x = 0, то y = 2 – вершина параболы (0,
2).б) Д(у) =(-?; ?)
в) Е(у)=[2; ?)
г) (-х)2 + 2 = х2 +2 – функция
четнаяд) Функция убывает на промежутке (-;0]
Функция возрастает на промежутке [0;).
Что изменилось в свойствах? (изменилась
область значений функции, изменились координаты
вершины параболы).
Как вы думаете, как будет расположен график
функции у = х2 – 2?
Постройте с помощью шаблона (Свойства устно).
III.
С помощью шаблона постройте график функции у
= – х2.
Свойства:
- вершина (0; 0)
- Д(у)=(-; )
- Е(у)= (-;)
- Функция четная – х2 = -(-х)2
- Функция возрастает на промежутке (-: 0],
- убывает на промежутке [0; ).
С помощью шаблона постройте график функции у
= -х2 + 2.
Работа по рисунку:
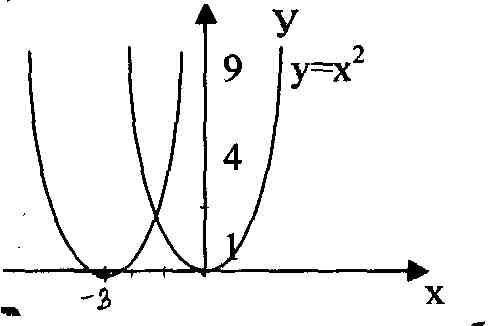
Рисунок 3
Определите вершину параболы (-3; 0)
y = (х + 3)2 – формула параболы
Свойства функции:
1). (-3; 0) – вершина параболы.
2). Д(у)=(-;
)3). E(у)=[0;)
4). Функция возрастает на промежутке [-3;+),
5). Функция убывает на промежутке (-;-3].
Постройте с помощью шаблона графики функций,
заданных формулами
1) y = х2 + 5
2) y = (х-1 )2.
Исследуйте одну на выбор.
IV. Домашнее задание
В одной координатной плоскости построить
графики функций
1) у = х2 + 3.
2) у = х2 – 3.
3) у = (х + 2)2
4) у = (х – 2)2
5) у = (х + З)2 – 1.
Исследовать эти функции.
Итог урока: на уроке мы научились строить
график параболы, задавать формулу параболы и
описывать ее свойства
Источник
МОУ СОШ №16 х. Пролетарского
Урок алгебры
в 7 классе
на тему
«Функция y = x2 и её график »
Разработала:
учитель математики
Драченко Е. Н.
2012 – 2013 учебный год
Тема урока: Функция y = x2 и её график.
Цели урока: ввести определение функции y = x2; изучить её свойства; научить строить и
читать график этой функции; показать прикладной характер изучаемого
материала; научить решать уравнения графическим способом;
развивать навыки исследовательской работы; графическую культуру учащихся;
воспитывать целенаправленное отношение к деятельности, аккуратность,
наблюдательность, интерес к окружающим явлениям.
Тип урока: урок изучения нового материала с использованием ИКТ.
Оборудование: компьютер, проектор, экран, компьютерные презентации; бланки
математического исследования; тексты самостоятельной работы.
Ход урока.
1.Организация начала урока.
Презентация «Функция y = x2 и её график». Слайды 1 – 2.
● Сообщение темы и цели урока.
2. Актуализация опорных знаний.
Слайды 3 – 6.
Устные упражнения.
● Назовите координаты точек, симметричных точкам (2; 6); (-1; 4); (0; 0); (-3; -5)
относительно оси y.
● Найдите значения функции y = 5x + 4, если х = – 1; – 2; 3; 5.
● Укажите область определения функции: y = 16 – 5x; y = y = y =
Повторение теоретических сведений.
● Расшифруйте предложенные термины.
Зависимость между двумя переменными, при которой
Функция каждому значению независимой переменной соответствует
единственное значение зависимой переменной.
Аргумент Независимая переменная, значения которой выбирают
произвольно.
График функции Множество всех точек координатной плоскости, абсциссы
которых равны значениям аргумента, а ординаты –
соответствующим значениям функции.
Область определения. Все значения, которые принимает независимая переменная.
Линейная функция. Функция, заданная формулой вида y = kx + b, где х –
переменная, k и b некоторые числа.
3. Изучение нового материала.
Слайд 7.
● Итак, мы уже знаем, что функция или функциональная зависимость – это зависимость между двумя переменными, при которой каждому значению одной переменной соответствует единственное значение другой переменной. Как известно, всякая функция описывает процессы движения и изменения, происходящие в окружающем нас мире.
● Рассмотрим, например, зависимость площади квадрата от его стороны.
– Что будет происходить с площадью квадрата, если мы будем изменять длину его стороны?
– Сторону квадрата увеличили в 3 раза. Как измениться его площадь?
– А если сторону уменьшить в 4 раза, что произойдёт тогда?
– Какой формулой задаётся зависимость площади квадрата от его стороны?. (S = a2)
– Будет ли зависимость площади квадрата от его стороны являться функцией? Объясните ответ.
● Если в формуле S = a2 площадь обозначить через y, а длину стороны через х, то рассмотренная нами функции задаётся формулой вида y = x2, которую называют квадратичной.
Слайды 8 – 10.
● По словам французского писателя Оноре де Бальзака «Ключом ко всякой науке является вопросительный знак». Поэтому мы сейчас проведём небольшое математическое исследование и попытаемся ответить на вопросы: что представляет собой функцияy = x2?; какими свойствами она обладает?; как выглядит её график? Все результаты исследований вы будете заносить в протокол исследования. (У каждого ребёнка на парте специальный бланк). (Приложение).
● Работу начнём с того, что составим таблицу соответственных значений x и y рассматриваемой нами функции. (Задание №1 математического исследования).
Дети самостоятельно заполняют таблицу, можно использовать таблицу квадратов двузначных чисел.
x
– 3
– 2,5
– 2
– 1,5
– 1
– 0,5
0,5
1
1,5
2
2,5
3
y
● Проверьте ваши результаты. (Правильные ответы на слайде).
● Выполним Задание №2. Построим график функции.
По данным таблицы учащиеся строят график функции, учитель оказывает необходимую помощь «слабым» детям.
● Давайте посмотрим, что у нас получилось. (Изображение графика на слайде).
● Итак, мы построили кривую, которая является графиком функции y = x2. Ясно, что этот график неограниченно продолжается вверх, справа и слева от оси y. Обратите внимание, ребята, на вид графика вблизи начала координат. Для значений х, близких к нулю, график практически сливается с прямой Ох. В таком случае говорят, что кривая касается оси абсцисс.
● График функции y = x2 называют параболой. Откуда взялось это название и что оно означает?
Презентация «Многоликая парабола».
Историческая справка.
Древнегреческий математик Аполлоний Пергский где – то за 200 лет до нашей эры разрезав конус, линию среза назвал параболой, что в переводе с греческого означает «приложение» или «притча», о чём математик и написал в восьмитомнике «Конические сечения». И долгое время параболой называли лишь линию среза конуса, пока не появилась квадратичная функция.
● Параболу часто можно встретить на практике.
Знаете ли вы, что:
Траектория камня, брошенного под углом к горизонту, летящего футбольного или баскетбольного мяча, артиллерийского снаряда является параболой (при отсутствии сопротивления воздуха). То есть всё, что мы бросим под углом к горизонту, будет лететь по параболе, поскольку движение под действием гравитации подчиняется законам квадратичной функции.
Струйки воды фонтана также описывают траекторию в виде параболы.
Форму параболы принимают орбиты комет, спутников и космических кораблей.
Парабола обладает оптическим свойством: все лучи, исходящие из источника света, находящегося в фокусе параболы (определённой точке), отражаются параллельно её оси. Это свойство параболы используется при изготовлении прожекторов, автомобильных фар, карманных фонариков, а также параболических антенн.
● Многоликую параболу можно встретить и в природе.
Невероятно, но факт!
Например, перевал в горном районе Ергаки (Саяны, Сибирь) напоминает по форме параболу. Он так и называется перевал Парабола.
Или вот это дерево!
Презентация «Функция y = x2 и её график». Слайды 11 – 15.
● Продолжим наше исследование. Наша задача выяснить, какими свойствами обладает функция y = x2 и как эти свойства отражаются на её графике. Для этого выполните Задание №4.
Опираясь на таблицу значений и график функции, учащиеся заполняют таблицу в бланке исследования, получая при этом свойства функции и отражение этих свойств на графике.
Учитель контролирует работу и оказывает необходимую помощь.
● Обсудим свойства функции y = x2.
Учащиеся формулируют свойства, а учитель, с помощью детей, комментирует их и делает необходимые дополнения, используя слайды.
– Область определения функции D(f): любое число. Действительно, любое число х можно возвести во вторую степень.
– Если х = 0, то y = 0. График функции, следовательно, проходит через начало координат.
– Если х ≠ 0, то y > 0. Действительно, квадрат любого числа, отличного от нуля, есть число положительное. Значит, все точки графика функции, кроме точки (0; 0), лежат выше оси х, т. е. в I и II координатных четвертях.
– Исходя из того, что функция принимает только неотрицательные значения, т. е. y ≥ 0, можно сделать вывод, что область значений функции E(f): все значения y ≥ 0, . т. е. неотрицательные.
– Противоположным значениям х соответствует одно и то же значение y. Это следует из того, что (- х)2 = х2 при любом х. Например, (-3)2 = 32 = 9. Таким образом, точки графика, имеющие противоположные абсциссы, симметричны относительно оси y. Говорят, график функции симметричен относительно оси y. Заметим, что такие функции называются чётными.
Слайды 16.
● Ещё раз вернёмся к параболе и перечислим её геометрические свойства:
Геометрические свойства параболы.
– Обладает симметрий. Осью симметрии является ось ординат.
– Ось разрезает параболу на две части, которые называют ветвями параболы.
– Точка (0; 0), в которой смыкаются ветви, называется вершиной параболы.
– Парабола касается оси абсцисс.
4. Закрепление изученного материала.
● Русский писатель Л. Н. Толстой сказал: «Знание – орудие, а не цель». Давайте учиться использовать полученные вами сегодня знания как орудие для выполнения заданий различного характера.
Слайды 17 – 18.
● Начнём с элементарного.
Выполняя упражнения, учащиеся должны опираться на свойства функции и графика.
● Используя график функции y = x2(рис. 61 учебника), найдём:
а) значение функции, соответствующее значению аргумента, равному: 1,4; – 1,4; – 2,6; 3,1; – 3,1;
Учитывая симметрию графика относительно оси ординат достаточно определить значения y для неотрицательных значений х.
б) значения аргумента, при котором значение функции равно 4; 6;
Достаточно найти одно из значений, а другое значение будет ему противоположным.
в) несколько значений х, при которых значения функции меньше 4; больше 4.
● Выполните задание №1 Самостоятельной работы. (Приложение).
Слайд 19.
● Вспомните, как устанавливается принадлежность точки графику заданной функции?
● Определим, принадлежит ли графику функции y = x2точка:
а) P(-18; 324); б) R(- 99; – 9081); в) S(17; 279).
а) Точка P лежит во II координатной четверти, поэтому она может принадлежать графику. Подставляя координаты точки P в формулу, получим 324 = (-18)2; 324 = 324 – верное равенство. Точка P принадлежит графику функции.
б) Точка R лежит в IV координатной четверти, значит, она не может принадлежать графику, поскольку все точки графика функции y = x2 лежат в верхней полуплоскости, т. е. в I и II координатных четвертях.
в) Точка S лежит в I координатной четверти, она может принадлежать графику функции. Подставляя координаты точки в формулу, получим 279 = 172; 279 = 289 – неверное равенство. Точка S не принадлежит графику.
● Определите, не выполняя вычислений, какие из точек не принадлежат графику функции y = x2. Ответ объясните. (Упражнение выполняется устно).
(-1; 1); (-2; -4); (0; 8); (3; -9); (1,8; 3,24); (16; 0).
● При каких значениях aточка P(a; 64) принадлежит графику функции y = x2. (Упражнение №492 учебника).
● Выполните задание №2 Самостоятельной работы. (Приложение).
Слайд 20.
● С помощью графиков функций можно найти приближённые значения корней некоторых уравнений, т. е. решить уравнение графическим способом. Разберём на примерах данный способ решения. Решим графическим способом уравнения:
а) х2 = 5; б) х2 = – 1; в) х2 = х + 1.
Объяснение ведётся согласно учебнику (Пример 1).
● Следовательно, алгоритм решения уравнения графическим способом состоит в следующем:
1. Построить в одной системе координат графики функций, стоящих в левой и правой части
уравнения.
2. Найти абсциссы точек пересечения графиков. Это и будут корни уравнения. Если точек пересечения нет, значит, уравнение не имеет корней.
● Выполните задание №3 Самостоятельной работы. (Приложение).
5. Контрольные вопросы.
● Как называется график функции y = x2?
● Как на координатной плоскости расположен график функции y = x2?
● Какова область определения функции y = x2?
Слайд 21 .
6. Рефлексия
Слайд 22 .
7. Домашнее задание.
● Изучить п.23.
● Выполнить упражнения №484; №486; №487; №494(а).
Слайд 23.
8. Удачи вам!
Источник
Математика: Свойства функций
Свойства функции разберем на примере о графика произвольной функции y = f (x):
- Область определения функции — это множество всех значений переменной x, которые имеют соответствующие им значения функции. Обозначают: D(f).На графике область определения — это промежутки на оси ОX, над которыми (или под которыми) имеются части графика. Для нашего примера D(f) = [-8; 9,4].
- Область значений функции — это множество всех ее значений у. Обозначают: E(f).На графике область значений функции — это промежутки на оси OY, слева или справа от которых (в горизонтальной полосе) находятся части графика.Для нашего примера Е(f) = [-4; 4,2].
- Функция y = f (x) называется возрастающей, если для любой пары значений аргументов x1, x2 из неравенства x1 < x2 следует неравенство f (x1) < f (x2).Функцию можно назвать возрастающей на промежутке, если большему из любых двух взятых из него чисел всегда соответствует большее значение функции.Для нашего примера функция возрастает при .Функция y = f (x) называется убывающей, если для любой пары значений аргументов x1, x2 из неравенства x1 < x2 следует неравенство f (x1) > f (x2).Функцию можно назвать убывающей на промежутке, если из любых двух взятых из него чисел большему из них всегда соответствует меньшее значение функции.Для нашего примера функция убывает при .
- Промежутки знакопостоянства — промежутки, на которых значения функции имеют постоянный знак (положительный или отрицательный).Промежуток положительного знака — это множество значений переменной x, у которых соответствующие значения функции больше нуля (y > 0).На графике — это части оси абсцисс, у которых соответствующие кусочки графика выше оси ОХ. Без графика их тоже можно найти, составив и решив неравенство f (x) > 0.Для нашего примера функция положительна при .Промежуток отрицательного знака — это множество тех значений переменной х, у которых соответствующие значения функции меньше нуля (y < 0).На графике — это промежутки оси абсцисс, у которых соответствующие кусочки графика ниже оси ОХ. Без графика их тоже можно найти, составив и решив неравенство f (x) < 0.Для нашего примера функция отрицательна при .
- Нули функции — это значения переменной х, при которых у (х) = 0.Без графика нули функции тоже можно найти, составив и решив уравнение f (x) = 0.По графику нули определяют как абсциссы точек пересечения графика с осью ОХ.Для нашего примера нули функции это точки х1 = -3, х2 = 2, х3 = 5.
- Четность и нечетность функции.Функция называется четной, если ее график симметричен относительно оси ОУ и для любого x ϵ D(f) верно: -х ϵ D(f) и f (-x) = f (x).Т.е. функция называется четной, если любым двум противоположным значениям аргумента, из области определения, соответствуют равные значения функции.На графике четная функция имеет ось симметрии OY.Функция называется нечетной, если ее область определения симметрична относительно нуля и для любого x ϵ D(f) верно: -х ϵ D(f) и f (-x) = -f (x).Т.е. функция называется нечетной, если любым двум противоположным значениям аргумента соответствуют противоположные значения функции.На графике нечетная функция симметрична относительно начала координат.Произведение или частное двух четных функций — есть функция четная.Произведение или частное двух нечетных функций — есть функция четная.Произведение или частное двух функций, одна из которых четная, а другая нечетная — есть функция нечетная.Функция нашего примера — ни четная, ни нечетная.
- Периодичность функции.Функция y = f (x) называется периодической с периодом Т > 0, если для любого x ϵ D(f) верно: (х — Т) ϵ D(f), (х + Т) ϵ D(f) и f (х — Т) = f (х + Т) = f (x).Если Т > 0 является периодом функции y = f (x), то число — период функции y = f (kx + b).Если Т1 > 0 и Т2 > 0 — периоды соответствующих функций y = f (x) и y = g (x), причем , где m, n ϵ N, , то любая комбинация этих функций y = a • f (x) + b • g(x), a, b ϵ Z, также периодическая, период которой равен T = HOK(T1, T2).Функция нашего примера не является периодической.
- Точки экстремума функции (точки максимума и минимума).Точка х0 называется точкой минимума, если для всех х ϵ D(f) в некоторой окрестности этой точки выполняется равенство f (x) ≥ f (x0).На графике точки минимума — это абсциссы, в которых график выглядит как «ямка».Для нашего примера точки минимума — это х1 = -4,5, х2 = 3.Точка х0 называется точкой максимума, если для всех х ϵ D(f) в некоторой окрестности этой точки выполняется равенство f (x) ≤ f (x0).На графике точки максимума — это абсциссы, в которых график выглядит как «горка».Для нашего примера точки максимума — это х1 = -7, х2 = -1, х3 = 7.
- Наименьшее и наибольшее значение функции.Число y = t называется наименьшим значением функции на промежутке [a, b], если для любого значения аргумента х ϵ [a, b] из этого промежутка верно неравенство t ≥ f (x).Для нашего примера наибольшее значение функции на промежутке [-8; 9,4] равно ун/б = 4,2.Число y = t называется наибольшим значением функции на промежутке [a, b], если для любого значения аргумента х ϵ [a, b] из этого промежутка верно неравенство t ≤ f (x).Для нашего примера наименьшее значение функции на промежутке [-8; 9,4] равно ун/м = -4.
Свойства элементарных функций
- Линейная функция f (x) = kx + b.D(f) = R, E(f) = R.График функции y = kx + b — прямая линия. Функция монотонно возрастает при k > 0 и убывает при k < 0. При b = 0 прямая линия проходит через начало координат, при этом функция y = kx — нечетная. Промежутки постоянного знака для функции y = kx зависят от знака параметра k:k > 0, то y > 0 при x > 0; y < 0 при x < 0;k < 0, то y > 0 при x < 0; y < 0 при x > 0.
- Квадратичная функция f(x) = ах2 + bх + с, а ≠ 0. Графиком является парабола.
Функция
Область определения
R
R
Вершина параболы
(0; 0)
Нули функции
x = 0
Экстремумы
если a < 0, то минимум в вершине
если a > 0, то максимум в вершинеОбласть значений
Четность
четная
ни четная, ни нечетная
- Степенная функция f (x) = хn, n ≥ 2, n ϵ N. Графиками ее являются квадратичные или кубические параболы.
Функция
Область определения
R
R
Область значений
R
[0; +∞ )
Четность
нечетная
четная
Нули функции
х =0
х =0
Экстремумы
нет
х = 0 — точка минимума
Монотонность
возрастает при х ϵ R
при х ≤ 0 убывает
при х > 0 возрастает - — частный случай дробно-рациональной функции. Графиками ее являются гиперболы соответствующей степени. Заметим, что
Функция
Область определения
R кроме х = 0
R кроме х = 0
Область значений
(-∞ ; 0) U (0; +∞ )
(0; +∞ )
Четность
нечетная
четная
Нули функции
нет
нет
Экстремумы
нет
нет
Монотонность
убывает при x ϵ D(f) при х < 0 возрастает
при х > 0 убывает - Степенная функция
Функция
Область определения
Область значений
Нули функции
х = 0
х = 0
Экстремумы
нет
нет
Монотонность
возрастает при х ϵ D(f)
возрастает при х ϵ D(f)
- Показательная функция
Функция
y = ax, 0 < a < 1
y = ax, a > 1
Область определения
R
R
Область значений
( 0; +∞ )
( 0; +∞ )
Нули функции
нет
нет
Экстремумы
нет
нет
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
- Логарифмическая функция
Функция
y = logax, 0 < a < 1
y = logax, a > 1
Область определения
( 0; +∞)
( 0; +∞)
Область значений
R
R
Нули функции
нет
нет
Экстремумы
нет
нет
Монотонность
убывает при х ϵ D ( f )
возрастает при х ϵ D ( f )
- — тригонометрические функции.
Функция
y = sin x
y = cos x
Область определения
R
R
Область значений
[-1; 1 ]
[-1; 1 ]
Нули функции
Четность
нечетная
четная
Периодичность
Экстремумы
Монотонность
возрастает при
убывает при
возрастает при
убывает при
- — тригонометрические функции.
Функция
y = tg x
y = ctg x
Область определения
R кроме
R кроме
Область значений
R
R
Нули функции
Четность
нечетная
нечетная
Периодичность
Монотонность
возрастает при
убывает при
- — обратные тригонометрические функции.
Функция
y = arcsin x
y = arcos x
Область определения
[-1; 1 ]
[-1; 1 ]
Область значений
Нули функции
x = 0
x = 1
Четность
нечетная
ни четная, ни нечетная
Монотонность
возрастает при x ϵ [-1; 1 ]
убывает при x ϵ [ -1 ; 1 ]
- — обратные тригонометрические функции
Функция
y = arctg x
y = arcctg x
Область определения
R
R
Область значений
Нули функции
x = 0
нет
Четность
нечетная
нечетная
Монотонность
возрастает при x ϵ R
убывает при x ϵ R
- Иррациональные функции вида .
Функция
Область определения
R
[0; +∞ )
Область значений
R
[0; +∞ )
Нули функции
х = 0
х = 0
Экстремумы
нет
нет
Монотонность
возрастает при х ϵ D ( f )
возрастает при х ϵ D ( f )
Обратные функцииОбратимой называют функцию, принимающую каждое свое значение в единственной точке области определения.Например, у = х2 необратима на R, т.к. уравнение f (х) = х2 имеет два решения:. Однако, у = х2 обратима на множестве х ≥ 0 или на множестве х ≤ 0, где выполняется единственность решения.Функцию f-1(x) называют обратной к функции f (x), если функция f-1(x) в каждой точке области значений обратимой функции f принимает такое значение у, что f (y) = x.Например, функцией, обратной к функции f (x) = kx + b, является функция:Свойства обратных функций
- Область значений функции f-1(x) является областью определения функции f (x).E(f-1(x)) = D(f), E(f) = D(f-1(x)).
- Графики функции f (x) и обратной к ней f-1(x) симметричны относительно биссектрисы у = х.
- Если функция f (x) монотонна на промежутке Х, то она обратима на этом промежутке.
- Если функция f (x) возрастает (убывает) в своей области определения, то и обратная к ней f-1(x) тоже возрастает (убывает).
Пример 1.Найти область значений функции РешениеПо определению синуса: -1 ≤ sinx ≤ 1. Умножим данное неравенство на 5:-5 ≤ 5sin x ≤ 5, затем вычтем из всех частей неравенства 2, получим: -7 ≤ 5sin x — 2 ≤ 3.Ответ: [-7; 3].Пример 2.Указать множество значений функции y = 5 — 2хРешение1-й способ.Симметрично оси ОХ отобразим график показательной функции у = 2х, чтобы получить график у = -2х. Затем последнюю функцию поднимем на 5 единиц вверх по оси ОУ. Видим, что область значений нашей функции — это луч (-∞; 5).2-й способ.2х > 0. Умножим данное неравенство на (-1), получим -2х < 0. Прибавим к обеим частям неравенства 5, получим 5 — 2х < 5. Т.е. Е (у) = (-∞; 5).Ответ: (-∞; 5).Пример 3.Найти область определения функции РешениеПо определению логарифмической функции -х2 + 5х — 4 > 0. По теореме, обратной к теореме Виета, найдем корни квадратного уравнения: х1 = 1, х2 = 4 и разложим квадратный трехчлен на множители: -(х — 1)(х — 4) > 0. Применяя метод интервалов для решения неравенства, получим х ϵ (1; 4).Ответ: (1; 4).Пример 4.Найти множество значений функции РешениеВыразим х через у: 6х + 7 = 3у — 10ху; х(6 + 10у) = 3у — 7.Если 6 + 10у = 0, то у = -0,6. Подставляя это значение у в последнее уравнение, получим:0х = -8,8. Данное уравнение корней не имеет, значит, функция не принимает значения равного -0,6.Если 6 + 10у ≠ 0, то . Область определения последнего уравнения — любое действительное у, кроме у = -0,6. Получаем, что Е(у) = (-∞; -0,6) U (-0,6; +∞).Ответ: (-∞; -0,6) U (-0,6; +∞).Пример 5.Найти множество значений функции РешениеУчитывая, что , по свойствам неравенств получим . Т.е. Е (у) = [-3; +∞).Ответ: [-3; +∞).Пример 6.Найти множество значений функции РешениеТак как Е(х2) = [0; +∞), то Е(х2 + 3) = [3; +∞). Так как обратная пропорциональность — непрерывная и убывающая функция на этом промежутке, большему значению аргумента будет соответствовать меньшее значение функции. При стремлении аргумента этой функции к +∞ значение самой функции стремится к нулю: Е (1 / (х2 + 3)) = (0; 1/3].Ответ: (0; 1/3].Пример 7.Найти множество значений функции РешениеЕ(х2) = [0; +∞), Е(х2 + 3) = [3; +∞). Так как функция непрерывна и возрастает на этом промежутке, то Ответ: .Пример 8.Найти наименьшее значение функции РешениеРазность принимает наименьшее значение при наибольшем значении вычитаемого. Дробь принимает наибольшее значение при наименьшем значении знаменателя. Получаем, что данная функция принимает наименьшее значение при наименьшем значении выражения , находящегося в знаменателе дроби.Итак, наименьшее значение знаменателя равно 1. Тогда функция принимает значение, равное -1.Ответ: -1.Список используемой литературы Видеолекция «Свойства функций»:
include ($_SERVER[‘DOCUMENT_ROOT’] . ‘/inc/ad-inc.htm’); ?>
Источник
