Какими свойствами обладает длина отрезок

ВОПРОСЫ
1. Сколько существует отрезков, концами которых являются две данные точки?

2. Как обозначают отрезок?

3. Какие вы знаете единицы длины?
Нам известны такие единицы длины: миллиметр, сантиметр, дециметр, метр, километр.
1 см – 10 мм
1 дм – 10 см
1 м – 100 см – 10 дм
1 км – 1000 м
4. Объясните, что означает измерить длину отрезка.

5. Каким свойством обладает длина отрезка?

6. Какие отрезки называют равными?

7. Какие длины имеют равные отрезки?

8. Какой из двух неравных отрезков считают большим?

9. Что называют расстоянием между точками А и В?

10. Объясните, какую геометрическую фигуру называют ломаной.

11. Что называют длиной ломаной?

12. Какую ломаную называют замкнутой?

РЕШАЕМ УСТНО
1. Какое число больше числа 46 на 9? Какое число меньше числа 72 на 15? Какое число больше числа 21 в 7 раз? Какое число меньше числа 65 в 13 раз?
55, 57, 147, 5
2. Назовите все двузначные числа, сумма цифр которых равна 6.
15, 24, 33, 42, 51, 60
3. Назовите все двузначные числа, разность цифр которых равна 7.
18, 29, 70, 81, 92
4. Назовите три последовательных натуральных числа, наименьшим из которых является наибольшее четырехзначное число.
9999, 10000, 10001
5. Назовите три последовательных натуральных числа, наибольшим из которых является наименьшее четырехзначное число.
9997, 9998, 9999
6. Выразите в сантиметрах:
1) 7 дм 4 см = 74 см
2) 4 м 1 см = 401 см
3) 2 м 6 дм = 260 см
4) 1 м 2 дм 5 см = 125 см
7. Выразите в дециметрах и сантиметрах:
1) 72 см = 7 дм 2 см
2) 146 см = 14 дм 6 см
3) 450 мм = 4 дм 5 см
4) 8 м 40 мм = 80 дм 4 см
УПРАЖНЕНИЯ
44. Запишите все отрезки, изображенные на рисунке 15.

a) AB, BC, AC, BK
б) OP, OR, OT, PR, PT, RT
в) AE, EC, CD, AC, ED, AD
г) MN, NE, ME, EP, PQ, EQ, MQ, NP
45. Запишите все отрезки, изображенные на рисунке 16.

а) AO, OC, AC, BO, OD, BD, AD
б) MK, KN, NP, MN, KP, MP, FK, KE, FE, EN, NS, ES
46. Отметьте в тетради точки A, B, C, D и соедините их попарно отрезками. Сколько отрезков образовлось? Сколько образовалось отрезков с концом в точке А?

47. Начертите отрезки MN и AC так, чтобы MN=6 см 3 мм, AC = 5 см 3 мм.

48. Начертите отрезки EF и BK так, что EF = 9 см 2 мм, BK = 7 см 6 мм.

49. Начертите отрезок АВ, длина которого равна 8 см 9 мм. Отметьте на нём точку С так, чтобы СВ = 3 см 4 мм. Какова длина отрезка АС?

50. Начертите отрезок TP, длина которого равна 7 см 8 мм. Отметьте на нём точку Е так, чтобы ТЕ = 2 см 6 мм. Какова длина отрезка ЕР?

51. Сравните на глаз отрезки АВ и CD (рис. 17). Проверьте свой вывод измерением.

52. Назовите все ломаные, изображённые на рисунке 11. Какая из них имеет наибольшее количество звеньев?

53. Назовите звенья ломаной, изображённой на рисунке 18, и измерьте их длины (в миллиметрах). Вычислите длину ломаной.

54. Запишите звенья ломаной, изображённой на рисунке 19, и измерьте их длины (в миллиметрах). Вычислите длину ломаной.

55. Отметьте в узле клеток тетради точку А; точку В разместите на 4 клетки левее и на 5 клеток выше точки А; точку С — на 3 клетки правее и на 1 клетку выше точки В; точку D — на 3 клетки правее и на 3 клетки ниже точки С; точку Е — на 1 клетку правее и на 2 клетки ниже точки D. Соедините последовательно отрезками точки А, В, С, D и Е. Какая фигура образовалась? Запишите её название и укажите количество звеньев.

56. Вычислите длину ломаной ABCDE, если АВ = 8 см, ВС = 14 см, CD = 23 см, DE = 10 см.

57. Вычислите длину ломаной MNKPEE, если MN = 42 мм, NK = 38 мм, КР = 19 мм, РЕ = 12 мм, ЕF = 29 мм.

58. Начертите в тетради ломаную, изображённую на рисунке 20. Измерьте длины звеньев (в миллиметрах) и найдите длину ломаной.

59. Известно, что отрезок SK в 3 раза больше отрезка RS (рис. 21). Найдите длину отрезка RK, если RS = 34 см.

60. Известно, что отрезок DВ в 5 раз меньше отрезка AD (рис. 22). Найдите длину отрезка АВ, если АD = 135 см.

61. Известно, что AC = 32 см, ВС = 9 см, CD = 12 см (рис. 23). Найдите длины отрезков АВ и BD.

62. Известно, что MF= 43 см, МЕ = 26 см, КЕ = 18 см (рис. 24). Найдите длины отрезков МК и EF.

63. Даны две точки А и В. Сколько можно провести отрезков, соединяющих эти точки? Сколько можно провести ломаных, соединяющих эти точки?

64. Начертите отрезок МК и отметьте на нём точки А и С. Запишите все образовавшиеся отрезки.

65. Длина отрезка АВ равна 28 см. Точки М и К принадлежат этому отрезку, причём точка К лежит между точками М и В, AM =12 см, ВК = 9 см. Найдите длину отрезка МК.

66. Точка С принадлежит отрезку АВ, длина отрезка АС равна 15 см, а отрезок АВ на 5 см больше отрезка АС. Чему равна длина отрезка ВС? Есть ли в условии задачи лишние данные?

67. Отрезки МТ и FK равны (рис. 25). Сравните отрезки MF и ТК.

68. Постройте ломаную ACDM так, чтобы АС = 15 мм, CD = 24 мм, DM = 32 мм. Вычислите длину ломаной.

69. Постройте ломаную CEFK так, чтобы звено СЕ было равно 8 мм, звено EF было на 14 мм больше звена СЕ, а звено FK — на 7 мм меньше звена EF. Вычислите длину ломаной.

70. Вычислите длину ломаной, изображённой на рисунке 26.

71. Известно, что АС = 8 см, BD = 6 см, ВС = 2 см (рис. 27). Найдите длину отрезка AD.

72. Известно, что MF = 30 см, ME = 18 см, KF = 22 см (рис. 28). Найдите длину отрезка КЕ.

73. Известно, что КР = РЕ = EF = FT = 2 см (рис. 29). Какие ещё равные отрезки есть на этом рисунке? Найдите их длины.

74. На первом отрезке отметили семь точек так, что расстояние между любыми соседними точками равно 3 см, а на втором — десять точек так, что расстояние между любыми соседними точками равно 2 см. Расстояние между какими крайними точками больше: лежащими на первом отрезке или лежащими на втором отрезке?

75. Известно, что АЕ = 12 см, AQ = QB, ВМ = МС, СК = KD, DR = RE, МК = 4 см (рис. 30). Найдите длину отрезка QR.

76. Какое наименьшее количество точек надо отметить на отрезках, изображённых на рисунке 31, чтобы на каждом из них было две отмеченные точки, не считая концов отрезков?

77. У Миши есть линейка, на которой отмечены только 0 см, 5 см и 13 см (рис. 32). Как, пользуясь этой линейкой, он может построить отрезок длиной: 1) 3 см; 2) 2 см; 3) 1 см?

УПРАЖНЕНИЯ ДЛЯ ПОВТОРЕНИЯ
78. Вычислите:


79. Выполните действия:

80. Детскому саду подарили четыре ящика конфет по 5 кг в каждом и шесть ящиков печенья по 3 кг в каждом. На сколько килограммов больше подарили конфет, чем печенья?

81. Медведица Настасия Петровна заготовила на зиму семь бочонков мёда по 12 кг в каждом и 8 бочонков мёда по 10 кг в каждом. Сколько всего килограммов мёда заготовила Настасия Петровна?

82. В магазин привезли 240 кг бананов и 156 кг апельсинов. Треть привезённых фруктов продали в первый день, а остальные — во второй день. Сколько килограммов фруктов продали во второй день?

83. Кот Матроскин вырастил в своём саду 246 кг яблок и 354 кг груш. Шестую часть всех фруктов он отдал своим друзьям из детского сада, пятую часть всех фруктов — друзьям из школы, а остальное — в больницу. Сколько килограммов фруктов Матроскин отдал в больницу?

84. Укажите наименьшее натуральное число, сумма цифр которого равна 101.

Источник
Отрезок — это часть прямой, ограниченная двумя точками этой прямой.
Если к точкам $A$ и $B$ приложить линейку и по ней провести от $A$ к $B$ линию, то получится отрезок $AB$. Тот же отрезок можно обозначить $BA$.
Точки $A$ и $B$ называют концами отрезка $AB$.
$blacktriangleright$ Пример 1. Сколько отрезков изображено на рисунке?
Решение: Вспоминаем определение отрезка. Обращаем внимание, что буквы $K$ и $L$ — это обозначение прямой. Получаем отрезки $DC$, $CE$, $DE$.
Значит, всего на рисунке изображено $3$ отрезка.
Ответ: $3$ отрезка.
Отрезки можно сравнивать с помощью циркуля или линейки.
Отрезки равны, если при наложении их концы можно совместить. Равные отрезки имеют одинаковую длину.
Например, отрезок $AB$ равен $CD$. Это записывают так: $AB=CD$.
В геометрических фигурах принято равные отрезки отмечать одинаковым числом чёрточек.
На рисунке $AB=CD$ и $AD=BC$.
$blacktriangleright$ Пример 2. Найдите на рисунке равные отрезки. Сколько получилось пар равных отрезков?
Решение: Равные отрезки в геометрических фигурах отмечают равным количеством чёрточек, тогда $AO=OB$, $DO=OC$, $DA=CB$, $AC=DB$.
Всего получилось $4$ пары равных отрезков.
Ответ: $4$ пары.
Отрезок $AB$ является частью отрезка $AC$. Он короче отрезка $AC$, а отрезок $AC$ длиннее отрезка $AB$.
Отрезок, длина которого принята за единицу измерения, называют единичным отрезком.
С помощью единичного отрезка измеряют длины произвольных отрезков.
Возьмем отрезок $OM$ длиной $1$ см в качестве единичного. Тогда измерения удобно производить с помощью линейки.
Если отрезок $CD$ состоит из пяти частей, каждая из которых равна отрезку $OM$, то длина отрезка $CD$ равна $5$ см. Пишут: $CD=5$ см.
Длина отрезка — это число, которое показывает, сколько раз отрезок, длина которого принята за единицу (меру) длины, укладывается в измеряемом отрезке.
Длину отрезка $CD$ называют также расстоянием между точками $C$ и $D$.
Для измерения отрезков кроме сантиметров применяют и другие единицы длины: дециметр (дм), метр (м), миллиметр (мм), километр (км).
$10$ см $= 1$ дм;
$100$ см $= 1$ м;
$1$ см $= 10$ мм;
$1$ км $= 1000$ м.
$blacktriangleright$ Пример 3. Выразите в сантиметрах $2$ дм $8$ см.
Решение: $2$ дм $8$ см $=$ $20$ см $+$ $8$ см $=$ $28$ см.
Ответ: $28$ см.
$blacktriangleright$ Пример 4. Длина отрезка $AB=60$ см. Точки $M$ и $N$ в указанном порядке лежат на этом отрезке. Найдите длину отрезка $MN$, если $AM=13$ см, $NB=37$ см.
Решение: Сделаем чертёж.
Вот теперь видно, что отрезок $AB$ состоит из трех отрезков: $AM$, $MN$, $NB$.
$AM+NB=13+37=50$ см.
Осталось найти длину третьего отрезка, для этого из длины отрезка $AB$ отнимем полученную сумму: $MN=60-50=10$ см.
Значит, длина отрезка $MN$ составляет $10$ см.
Ответ: $10$ см.
Задачки от мистера Фокса
№1. Сколько отрезков изображено на рисунке?
Данный рисунок является дополнением к рисунку из задачи, которую мы разобрали выше. Отличается он тем, что провели еще одну прямую. Поэтому отрезки будут теми же — $DC$, $CE$, $DE$ — и плюс еще один отрезок — $FC$.
Значит, на рисунке всего $4$ отрезка.
Ответ: $4$ отрезка.
№2. Найдите на рисунке равные отрезки. Сколько на рисунке пар равных отрезков?
Ищем отрезки с одинаковым количеством чёрточек.
Получаем: $AD=DB$, $BE=EC$, $AF=FC$.
Значит, всего $3$ пары равных отрезков.
Ответ: $3$ пары.
№3. Выразите в дециметрах с сантиметрами $13$ см.
$13$ см $=$ $10$ см $+$ $3$ см $=$ $1$ дм $3$ см.
Ответ: $1$ дм $3$ см.
№4. Найдите длину отрезка $LM$ по данным рисунка.
Из рисунка видим, что $KM=78$, $KL=59$.
Найдем длину отрезка $LM$: $LM=78-59=19$.
Ответ: $LM=19$.
Источник
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Длина отрезка
Отрезок – это геометрическая фигура, которая имеет начало и конец, значит отрезки можно измерять.
Измерить отрезок – значит найти его длину(расстояние между его концами).
Для того, чтобы найти длину отрезка, его сравнивают с отрезком принятым за единицу измерения, который носит название единичный отрезок.
Если за единицу измерения принять сантиметр, то, чтобы определить длину отрезка, нужно узнать сколько раз в этом отрезке укладывается сантиметр. На рис.1 в отрезке СD сантиметр укладывается ровно три раза, значит, длина отрезка СD равна 3 см, можно записать СD = 3 см. В данном случае, для измерения удобно использовать сантиметровую линейку.
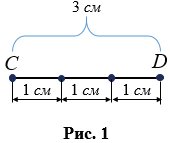
Бывает, что единичный отрезок не укладывается целое число раз в измеряемый отрезок, тогда единичный отрезок делят на 10 равных частей и определяют сколько раз одна десятая часть укладывается в остатке измеряемого отрезка. На рис.2 в отрезке СВ сантиметр укладывается 2 раза и в остатке 3 раза укладывается одна десятая часть сантиметра, значит, длина отрезка СВ равна 3,3 см или, учитывая что для сантиметра десятая часть равна миллиметру, 3 см 3 мм, т.е. можно записать СВ = 3,3 см (СВ = 3 см 3 мм).
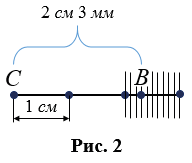
Может получится так, что и в миллиметрах остаток не укладывается целое число раз, тогда:
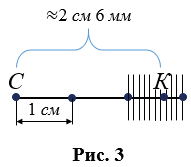
- Если нужны более точные измерения, то процесс деления продолжается, т.е. миллиметр также можно разделить на 10 равных частей и т.д. Такая точность в повседневной жизни не нужна, поэтому пользуются приближенными значениями, но имеет важную роль при проведении каких-либо исследований для совершения научных открытий.
За единицу измерения можно принимать не только сантиметр, но и другие отрезки, например, дециметр, метр и т.д.
Длина отрезка – это всегда какое-то положительное число.
Свойства длин отрезков:
- Равные отрезки имеют равные длины.
- Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков. Так на Рис.4 точка С делит отрезок АВ на два отрезка АС и СВ. Приложим линейку и видим, что АС = 4,5 см, СВ = 2,5 см, АВ = 7 см, т.е. АС + СВ = АВ.
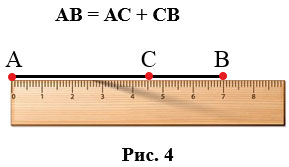
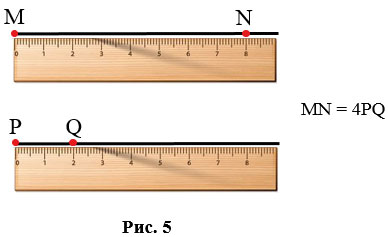
- Если длина одного отрезка MN в n раз больше длины другого отрезка PQ, то записывают MN = nPQ. На Рис.5 даны два отрезка MN и PQ, приложим к ним линейку и видим, что MN = 8 см, PQ = 2 см, т.е. MN больше PQ в 4 раза, тогда можно записать, что MN = 4PQ.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точки, прямые, отрезки
Провешивание прямой на местности
Луч
Угол
Равенство геометрических фигур
Сравнение отрезков
Сравнение углов
Единицы измерения длины, расстояний
Градусная мера угла
Измерение углов на местности
Смежные углы
Вертикальные углы
Перпендикулярные прямые
Построение прямых углов на местности
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 24,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 25,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 26,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 29,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 36,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 39,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 13,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 79,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 3,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 801,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Источник
В геометрии длина – это величина, характеризующая протяженность отрезка.
Определение. Длиной отрезка называется неотрицательная величина, обладающая следующими свойствами:
1) равные отрезки имеют равные длины;
2) если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.
Эти свойства длины отрезка используются при ее измерении. Чтобы измерить длину отрезка, нужно иметь единицу длины, такой единицей является длина произвольного отрезка. Результатом измерения длины отрезка х является неотрицательное действительное число, обозначим его т(х). Это число называют численным значением длины отрезка х при выбранной единице длины или просто длиной.
Такое число всегда существует и единственно. Для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
Из определения длины отрезка следуют известные свойства численных значений длин. Сформулируем некоторые из них, считая, что единица длины выбрана.
1. Если два отрезка равны, то численные значения их длин также равны, и обратно: если численные значения длин двух отрезков равны, то равны и сами отрезки.
х = y <=> т(х) = т(у)
2. Если отрезок х состоит из отрезков х, и х2, то численное значение его длины равно сумме численных значений длин отрезков х, и х2. Справедливо и обратное утверждение.
х = х1 х2 <=> т(х) = т(х1) + т(х2)
3. При замене единицы длины численное значение длины увеличивается (уменьшается) во столько раз, во сколько новая единица меньше (больше) старой.
4. Численное значение длины единичного отрезка равно единицы.
Рассмотрим процесс измерение длин отрезков. Из множество отрезков выбирают какой – нибудь отрезок е и принимают его за единицу длины. На отрезке а от одного из его концов откладывают последовательно отрезки, равные е, до тех пор, пока это возможно. Если отрезки, равные е отложились п раз и конец последнего совпал с концом отрезка а, то говорят, что значение длины отрезка а есть натуральное число п, и пишут а = пе. Если же отрезки, равные е, отложились п раз и остался еще остаток, меньшее, то на нем откладывают отрезки равные е1= 1/10 ∙е. Если они отложились точно п1 раз, то тогда а = п1е и значение длины отрезка а есть конечная десятичная дробь. Если же отрезок е1отложился п1 раз и остался еще остаток, меньшей е1, то на нем откладывают отрезки равные е2 = 1/100 ∙ е. Если представить этот процесс бесконечно продолжительным, то получим, что значение длины отрезка а есть бесконечная десятичная дробь.
Итак, при выбранной единицы длина любого отрезка выражается положительными числами.
На практике для измерения длин отрезков используются различные инструменты, в частности линейка с нанесенными на ней единицами длины.
При решении практических задач используются стандартные единицы длины: миллиметр (мм), сантиметр (см), метр (м), километр (км) и др.
Соотношение между ними:
1 километр (км) = 1000 метрам (м)
1 метр (м) = 10 дециметрам (дм) = 100 сантиметрам (см)
1 дециметр (дм) = 10 сантиметрам (см)
1 сантиметр (см) = 10 миллиметрам (мм)
Дата добавления: 2015-04-18; просмотров: 385; Нарушение авторских прав
Источник
- Длина отрезка
- Равные отрезки
- Сравнение отрезков
- Середина отрезка
Отрезок — это часть прямой, ограниченная двумя точками, лежащими на этой прямой. Точки, определяющие границы отрезка, называются концами отрезка.

Отрезок обозначается двумя большими латинскими буквами, поставленными при его концах: отрезок AB или BA.
Длина отрезка
Длина отрезка — это расстояние между концами отрезка. Любой отрезок имеет длину, бо́льшую нуля:

Измерение длины отрезка осуществляется путём сравнения данного отрезка с длиной единичного отрезка. Единичный отрезок — это отрезок, длина которого принимается за единицу. Следовательно:
длина отрезка – это положительное число, показывающее, сколько раз единичный отрезок и его части укладываются в данном отрезке.
Чаще всего используются единичные отрезки равные 1 мм, 1 см, 1 дм, 1 м или 1 км. Измерить длину отрезка можно линейкой или любым другим прибором для измерения длины:

AB = 6 см.
Свойства длин отрезков:
- Основное свойство длины отрезка: если точка делит отрезок на два отрезка, длина всего отрезка равна сумме длин этих двух отрезков.

- Длины равных отрезков равны.
- Любой отрезок имеет определённую длину, большую нуля.
Равные отрезки
Равные отрезки — это отрезки, имеющие одинаковую длину. Если наложить равные отрезки друг на друга, то их концы совпадут.
Пример. Возьмём два отрезка CD и LM:

Если расположить отрезки параллельно друг над другом так, чтобы точка C была над точкой L, то станет видно, что точка D располагается над точкой М:

Значит длины отрезков равны, следовательно CD = LM.
Сравнение отрезков
Сравнить два отрезка — это значит определить, равны они, или один больше другого.
Сравнить два отрезка можно, отложив на прямой оба отрезка из одной точки в одну и туже сторону. Для этого можно воспользоваться циркулем.
Чтобы отложить на прямой отрезок равный данному, сначала помещают ножки циркуля так, чтобы острия их концов упирались в концы отрезка, а затем, не изменяя раствора циркуля, переносят его так, чтобы оба его конца находились на прямой.

При сравнении двух отрезков возможно получение одного из представленных результатов: отрезки будут равны, первый отрезок будет больше второго или первый отрезок будет меньше второго.
Пример. Если отложить на прямой от любой точки, например C, в одну сторону два отрезка CA и CB и точка A окажется между точками C и B, то отрезок CA меньше отрезка CB (или CB больше отрезка CA):

CA < CB или CB > CA.
Если точка B окажется между точками C и A, то отрезок CA больше отрезка CB (или CB меньше отрезка CA):

CA > CB или CB < CA.
Если точки A и B совпадут, то отрезки CA и CB равны:

CA = CB.
Если при наложении отрезков оба их конца совмещаются, значит отрезки равны.
При сравнении отрезков путём измерения их длин больше будет тот отрезок, у которого больше длина.
Пример. Сравнить длину отрезков AB и AC.

Так как отрезок AB имеет большую длину, чем отрезок AC, то
AB > AC.

Так как отрезки AB и AC имеют одинаковую длину, то
AB = AC.
Если при измерении отрезков их длины равны, то и отрезки равны.
