Какими свойствами обладает деление плоскости на две полуплоскости 7 класс

§1. Контрольные вопросы
Вопрос 1. Приведите примеры геометрических фигур.
Ответ. Примеры геометрических фигур: треугольник, квадрат, окружность.
Вопрос 2. Назовите основные геометрические фигуры на плоскости.
Ответ. Основными геометрическими фигурами на плоскости являются точка и прямая.

Вопрос 3. Как обозначаются точки и прямые?
Ответ. Точки обозначаются прописными латинскими буквами: A, B, C, D, … . Прямые обозначаются строчными латинскими буквами: a, b, c, d, … .
Прямую можно обозначать двумя точками, лежащими на ней. Например, прямую a на рисунке 4 можно обозначить AC, а прямую b можно обозначить BC.
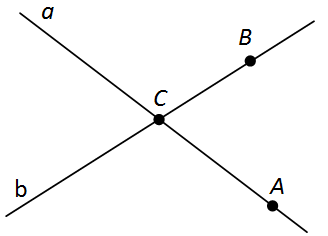
Рис.4
Вопрос 4. Сформулируйте основные свойства принадлежности точек и прямых.
Ответ. Какова бы ни была прямая, существуют точки, принадлежащие этой прямой, и точки, не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Вопрос 5. Объясните, что такое отрезок с концами в данных точках.
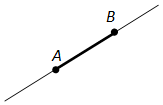
Ответ.Отрезком называется часть прямой, которая состоит из всех точек этой прямой, лежащих между двумя данными её точками. Эти точки называются концами отрезка. Отрезок обозначается указанием его концов. Когда говорят или пишут: “отрезок AB”, то подразумевают отрезок с концами в точках A и B.
Вопрос 6. Сформулируйте основное свойство расположения точек на прямой.
Ответ. Из трёх точек на прямой одна и только одна лежит между двумя другими.
Вопрос 7. Сформулируйте основные свойства измерения отрезков.
Ответ. Каждый отрезок имеет определённую длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Вопрос 8. Что называется расстоянием между двумя данными точками?
Ответ. Длину отрезка AB называют расстоянием между точками A и B.
Вопрос 9. Какими свойствами обладает разбиение плоскости на две полуплоскости?
Ответ. Разбиение плоскости на две полуплоскости обладает следующим свойством. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.
Вопрос 10. Сформулируйте основное свойство расположения точек относительно прямой на плоскости.
Ответ. Прямая разбивает плоскость на две полуплоскости.
Вопрос 11. Что такое полупрямая или луч? Какие полупрямые называются дополнительными?
Ответ.Полупрямой или лучом называется часть прямой, которая состоит из всех точек этой прямой, лежащих по одну сторону от данной её точки. Эта точка называется начальной точкой полупрямой. Различные полупрямые одной и той же прямой, имеющие общую начальную точку, называются дополнительными.
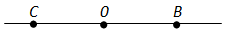
Вопрос 12. Как обозначаются полупрямые?
Ответ. Полупрямые, так же как и прямые, обозначаются строчными латинскими буквами.
Вопрос 13. Какая фигура называется углом?
Ответ. Углом называется фигура, которая состоит из точки – вершины угла – и двух различных полупрямых, исходящих из этой точки, – сторон угла.
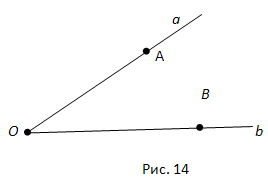
Вопрос 14. Как обозначается угол?
Ответ. Угол обозначается либо указанием его вершины, либо указанием его сторон, либо указанием трёх точек: вершины и двух точек на сторонах угла. Слово «угол» иногда заменяют знаком.
Вопрос 15. Какой угол называется развёрнутым?
Ответ. Если стороны угла являются дополнительными полупрямыми одной прямой, то угол называется развёрнутым.
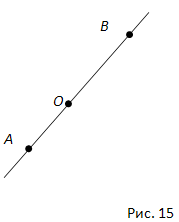
Вопрос 16. Объясните, что означает выражение: «Полупрямая проходит между сторонами угла”.
Ответ.
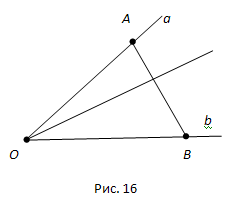
Мы будем говорить, что луч проходит между сторонами данного угла, если он исходит из его вершины и пересекает какой-нибудь отрезок с концами на сторонах угла.
Вопрос 17. В каких единицах измеряются углы и с помощью какого инструмента? Объясните, как проводится измерение.
Ответ.Углы измеряются в градусах при помощи транспортира.
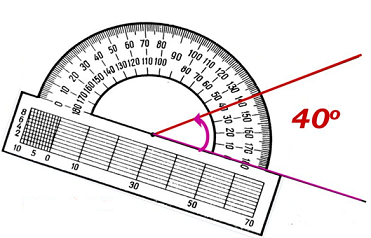
Вопрос 18. Сформулируйте основные свойства измерения углов.
Ответ. Каждый угол имеет определённую градусную меру, большую нуля. Развёрнутый угол равен 180°. Градусная мера угла равна сумме градусных мер углов, на которые он разбивается любым лучом, проходящим между его сторонами.
Вопрос 19. Сформулируйте основные свойства откладывания отрезков и углов.
Ответ. На любой полупрямой от её начальной точки можно отложить отрезок заданной длины, и только один. От любой полупрямой в заданную полуплоскость можно отложить угол с заданной градусной мерой, меньшей 180°, и только один.
Вопрос 20. Что такое треугольник?
Ответ.
Треугольником называется фигура, которая состоит из трёх точек, не лежащих на одной прямой, и трёх отрезков, попарно соединяющих эти точки. Точки называются вершинами треугольника, а отрезки — сторонами.

Вопрос 21. Что такое угол треугольника при данной вершине?
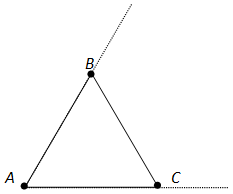
Ответ. Углом треугольника ABC при вершине A называется угол, образованный полупрямыми AB и AC. Так же определяются углы треугольника при вершинах B и C.
Вопрос 22. Какие отрезки называются равными?
Ответ. Отрезки называются равными, если их длины равны.
Вопрос 23. Какие углы называются равными?
Ответ. Углы называются равными, если их градусные меры равны.
Вопрос 24. Какие треугольники называются равными?
Ответ. Треугольники называются равными, если у них соответствующие стороны равны и соответствующие углы равны. При этом соответствующие углы должны лежать против соответствующих сторон.
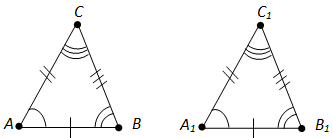
Вопрос 25. Как на рисунке отмечаются у равных треугольников соответствующие стороны и углы?
Ответ.На чертеже равные отрезки обычно отмечают одной, двумя или тремя чёрточками, а равные углы — одной, двумя или тремя дужками.
Вопрос 26. Объясните по рисунку 23 существование треугольника, равного данному.
Ответ.
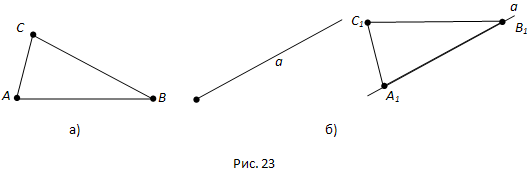
Пусть мы имеем треугольник ABC и луч a (рис. 23, а). Переместим треугольник ABC так, чтобы его вершина A совместилась с началом луча a, вершина B попала на луч a, а вершина C оказалась в заданной полуплоскости относительно луча a и его продолжения. Вершины нашего треугольника в этом новом положении обозначим A1,B1,C1 (рис. 23, б).
Треугольник A1B1C1 равен треугольнику ABC.
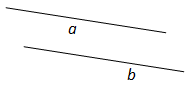
Вопрос 27. Какие прямые называются параллельными? Какой знак используется для обозначения параллельности прямых?
Ответ.Две прямые называются параллельными, если они не пересекаются. Для обозначения параллельности прямых используется знак
Вопрос 28. Сформулируйте основное свойство параллельных прямых.
Ответ. Через точку, не лежащую на данной прямой, можно провести на плоскости не более одной прямой, параллельной данной.
Вопрос 29. Приведите пример теоремы.
Ответ. Если прямая, не проходящая ни через одну из вершин треугольника, пересекает одну из его сторон, то она пересекает только одну из двух других сторон.
Источник
- Главная
- Вопросы & Ответы
- Вопрос 1286373
более месяца назад
Просмотров : 14
Ответов : 1
Лучший ответ:

В месте раздела плоскостей прерывается область интегрирования по площади и неопределенный интеграл вырождается в определенный. Разбиение разрывает непрерывную корреляцию между функцией и аргументами кривой, проходящей по обеим плоскостям, если вторая производная – не ноль
более месяца назад
Ваш ответ:
Комментарий должен быть минимум 20 символов
Чтобы получить баллы за ответ войди на сайт

Лучшее из галереи:































Другие вопросы:
говорят,что Москва ,если смотреть издалека на утренней морозной заре или в золотистых летних сумерках, вся была ,как этот сказочный златоглавый и островерхий град. схема этого предложения
более месяца назад
Смотреть ответ
Просмотров : 10
Ответов : 1
Упростите выражения:а) 8х-(3х 5) (2х-9) ;б) 2(х-1)-3(х-2) х ;в) -3,5 6 при х=2; -3; 0,4 ;г) 13х 39 21х 63 при х= -3 ;д) 2,1х 6,3-2,4х-6,2-5 при х= -3 .
более месяца назад
Смотреть ответ
Просмотров : 5
Ответов : 1
система 7х 2у=9 5х 2у=11 решить слособом сложениясистема 3х 5у=16 2х 3у=9 решить способом сложения
более месяца назад
Смотреть ответ
Просмотров : 8
Ответов : 1
при каком государе началось присоединение сибирских земель?помогите пожалуйста!
более месяца назад
Смотреть ответ
Просмотров : 8
Ответов : 1
Прямоугольник треугольника один из катетов больше медианы праведенный из вершины прямоугольного угла на 0,5 метра.Найдите площадь, если второй катет равен 4 метра.
более месяца назад
Смотреть ответ
Просмотров : 9
Ответов : 1
Источник
Гипермаркет знаний>>Математика>>Математика 7 класс>>Математика:Полуплоскости
Полуплоскости
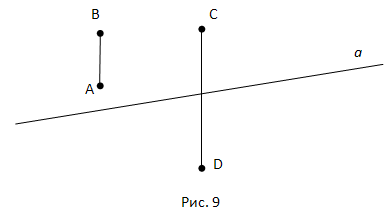
Посмотрите на рисунок 9. Прямая а разбивает плоскость на две полуплоскости. Это разбиение обладает следующим свойством. Если концы какого-нибудь отрезка принадлежат одной полуплоскости, то Отрезок не пересекает прямую. Если концы отрезка принадлежат разным полуплоскостям, то отрезок пересекает прямую.
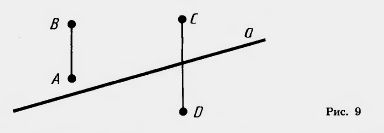
На рисунке 9 точки А и В лежат в одной из полуплоскостей, на которые прямая а разбивает плоскость. Поэтому отрезок АВ не пересекает прямую а. Точки С и D лежат в разных полуплоскостях. Поэтому отрезок CD пересекает прямую а.
Основным свойством расположения точек относительно прямой на плоскости мы будем называть следующее свойство:
IV. Прямая разбивает плоскость на две полуплоскости.
Задача (17). Даны прямая и три точки А, В, С, не лежащие на этой прямой. Известно, что отрезок АВ пересекает прямую, а отрезок АС не пересекает ее.
Пересекает ли прямую отрезок ВС? Объясните ответ.
Решение. Прямая разбивает плоскость на две полуплоскости (рис. 10).
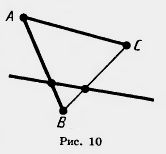
Точка А принадлежит одной из них. Отрезок АС не пересекает прямую. Значит, точка С лежит в той же полуплоскости, что и точка А.
Отрезок АВ пересекает прямую. Значит, точка В лежит в другой полуплоскости.
Таким образом, точки В и С лежат в разных полуплоскостях. А это значит, что отрезок ВС пересекает нашу прямую.
А. В. Погорелов, Геометрия для 7-11 классов, Учебник для общеобразовательных учреждений
Календарно-тематическое планирование по математике, видео по математике онлайн, Математика в школе скачать
Содержание урока
![]() конспект урока
конспект урока
![]() опорный каркас
опорный каркас
![]() презентация урока
презентация урока
![]() акселеративные методы
акселеративные методы
![]() интерактивные технологии
интерактивные технологии
Практика
![]() задачи и упражнения
задачи и упражнения
![]() самопроверка
самопроверка
![]() практикумы, тренинги, кейсы, квесты
практикумы, тренинги, кейсы, квесты
![]() домашние задания
домашние задания
![]() дискуссионные вопросы
дискуссионные вопросы
![]() риторические вопросы от учеников
риторические вопросы от учеников
Иллюстрации
![]() аудио-, видеоклипы и мультимедиа
аудио-, видеоклипы и мультимедиа
![]() фотографии, картинки
фотографии, картинки
![]() графики, таблицы, схемы
графики, таблицы, схемы
![]() юмор, анекдоты, приколы, комиксы
юмор, анекдоты, приколы, комиксы
![]() притчи, поговорки, кроссворды, цитаты
притчи, поговорки, кроссворды, цитаты
Дополнения
![]() рефераты
рефераты
![]() статьи
статьи
![]() фишки для любознательных
фишки для любознательных
![]() шпаргалки
шпаргалки
![]() учебники основные и дополнительные
учебники основные и дополнительные
![]() словарь терминов
словарь терминов
![]() прочие
прочие
Совершенствование учебников и уроков
![]() исправление ошибок в учебнике
исправление ошибок в учебнике
![]() обновление фрагмента в учебнике
обновление фрагмента в учебнике
![]() элементы новаторства на уроке
элементы новаторства на уроке
![]() замена устаревших знаний новыми
замена устаревших знаний новыми
Только для учителей
![]() идеальные уроки
идеальные уроки
![]() календарный план на год
календарный план на год
![]() методические рекомендации
методические рекомендации
![]() программы
программы
![]() обсуждения
обсуждения
Интегрированные уроки
Если у вас есть исправления или предложения к данному уроку, напишите нам.
Если вы хотите увидеть другие корректировки и пожелания к урокам, смотрите здесь – Образовательный форум.
Авторські права | Privacy Policy |FAQ | Партнери | Контакти | Кейс-уроки
© Автор системы образования 7W и Гипермаркета Знаний – Владимир Спиваковский
При использовании материалов ресурса
ссылка на edufuture.biz обязательна (для интернет ресурсов –
гиперссылка).
edufuture.biz 2008-© Все права защищены.
Сайт edufuture.biz является порталом, в котором не предусмотрены темы политики, наркомании, алкоголизма, курения и других “взрослых” тем.
Разработка – Гипермаркет знаний 2008-
Ждем Ваши замечания и предложения на email: 
По вопросам рекламы и спонсорства пишите на email: 
Источник
Инфоурок
›
Геометрия
›Презентации›Презентация “Полуплоскость и угол” (7 класс)

Описание презентации по отдельным слайдам:
1 слайд

Описание слайда:
Полуплоскость и угол Следующее свойство является аксиомой взаимного расположения точек на плоскости относительно данной прямой. Каждая прямая на плоскости разбивает эту плоскость на две части. При этом если две точки принадлежат разным частям, то отрезок, соединяющий эти точки, пересекается с прямой. Если две точки принадлежат одной части, то отрезок, соединяющий эти точки, не пересекается с прямой. Полуплоскостью называется … часть плоскости, состоящая из точек данной прямой и точек, … лежащих по одну сторону от этой прямой.
2 слайд

Описание слайда:
Угол его стороны вместе составляют одну прямую. одна сторона у них общая, а две другие … вместе составляют одну прямую. стороны одного угла дополняют до прямых стороны другого угла. одной из частей плоскости, ограниченной этими лучами. Общая вершина называется… вершиной угла. Сами лучи называются… сторонами угла. двумя лучами с общей вершиной и …
3 слайд

Описание слайда:
Равенство углов Одной из основных операций, которую можно производить с углами, является операция откладывания данного угла в ту или другую сторону от данного луча. Получающийся при этом угол называется равным исходному углу. В качестве аксиом принимаются следующие свойства. От любого луча на плоскости в заданную сторону можно отложить только один угол, равный данному. Все развернутые углы равны.
4 слайд

Описание слайда:
Виды углов он равен своему смежному углу. он меньше прямого угла. он больше прямого, но меньше развернутого угла.
5 слайд

Описание слайда:
Сложение углов Аналогичным образом поступают для вычитания из большего угла меньшего. Чтобы сложить два угла, например АОВ и CО1D, отложим угол CO1D от луча ОВ так, чтобы точки A и D находились по разные стороны от прямой ОВ. Обозначим ОЕ луч, в который перейдет луч О1D. Тогда угол АОЕ даст сумму углов АОВ и CО1D.
6 слайд

Описание слайда:
Вопрос 1 Ответ: На две части. На сколько частей прямая разбивает плоскость?
7 слайд

Описание слайда:
Вопрос 2 Ответ: а) Если отрезок, соединяющий эти точки, пересекается с прямой. В каком случае две точки принадлежат: а) одной полуплоскости; б) разным полуплоскостям относительно данной прямой? б) если отрезок, соединяющий эти точки, не пересекается с прямой.
8 слайд

Описание слайда:
Вопрос 3 Какая фигура называется углом? Что называется вершиной угла? Что называется сторонами угла? Ответ: Фигура, образованная двумя лучами с общей вершиной и одной из частей плоскости, ограниченной этими лучами, называется углом. Общая вершина называется вершиной угла, а сами лучи – сторонами угла.
9 слайд

Описание слайда:
Вопрос 4 Какой угол называется развернутым? Ответ: Угол называется развернутым, если его стороны вместе составляют прямую.
10 слайд

Описание слайда:
Вопрос 5 Какие углы называются смежными? Ответ: Два угла называются смежными, если одна сторона у них общая, а две другие составляют вместе прямую.
11 слайд

Описание слайда:
Вопрос 6 Какие углы называются вертикальными? Ответ: Два угла называются вертикальными, если стороны одного угла дополняют до прямых стороны другого угла.
12 слайд

Описание слайда:
Вопрос 7 Как обозначаются углы?
13 слайд

Описание слайда:
Вопрос 8 Какие два угла называются равными? Ответ: Два угла называются равными, если один получается из другого операцией откладывания угла.
14 слайд

Описание слайда:
Вопрос 9 Как сложить два угла? Ответ: Чтобы сложить два угла, например АОВ и CО1D, отложим угол CO1D от луча ОВ так, чтобы точки A и D находились по разные стороны от прямой ОВ. Обозначим ОЕ луч, в который перейдет луч О1D. Тогда угол АОЕ даст сумму углов АОВ и CО1D.
15 слайд

Описание слайда:
Вопрос 10 Как обозначается сумма углов AOB и CQD?
16 слайд

Описание слайда:
Вопрос 11 В каком случае говорят, что угол АOВ меньше угла А1O1В1? Ответ: Если при откладывании угла АOВ от луча O1В1 луч OВ переходит в луч O1B’, лежащий между лучами O1А1 и O1В1, то говорят, что угол АOВ меньше угла А1O1В1.
17 слайд

Описание слайда:
Вопрос 12 Как обозначается то, что угол AOB меньше угла CQD?
18 слайд

Описание слайда:
Вопрос 13 Как из большего угла вычесть меньший? Ответ: Чтобы из большего угла CQD вычесть меньший угол AOB, от луча QC отложим угол CQB’, равный углу AOB. Угол B’QD будет разностью отрезков СQD и AOB.
19 слайд

Описание слайда:
Вопрос 14 Ответ: а) Угол, равный свое?
