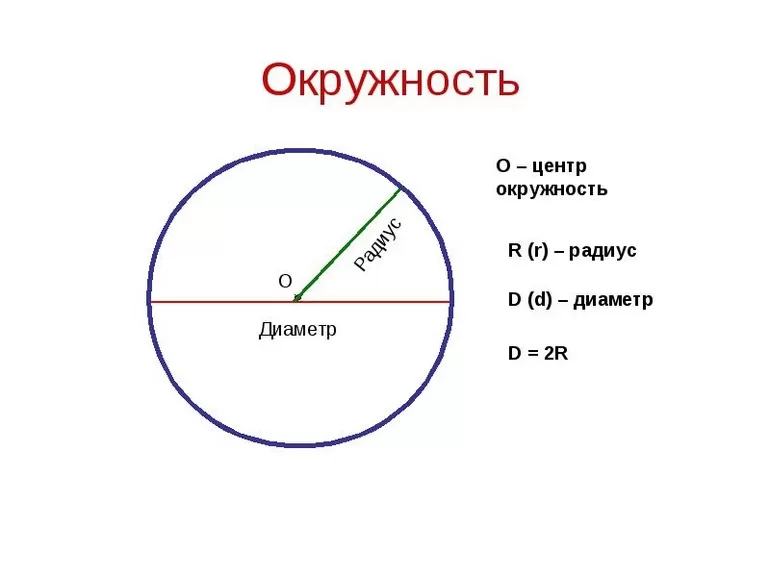
Какими свойствами обладает четырехугольник вписанный в окружность

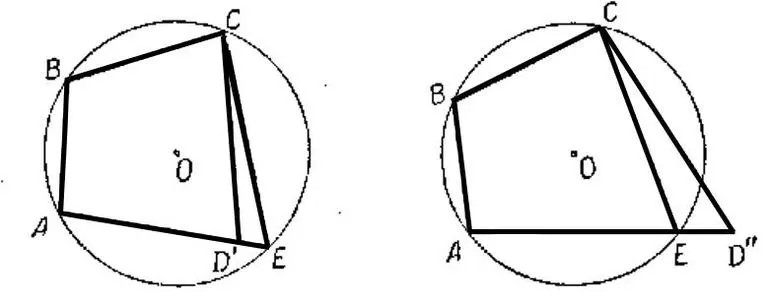
Общие сведения
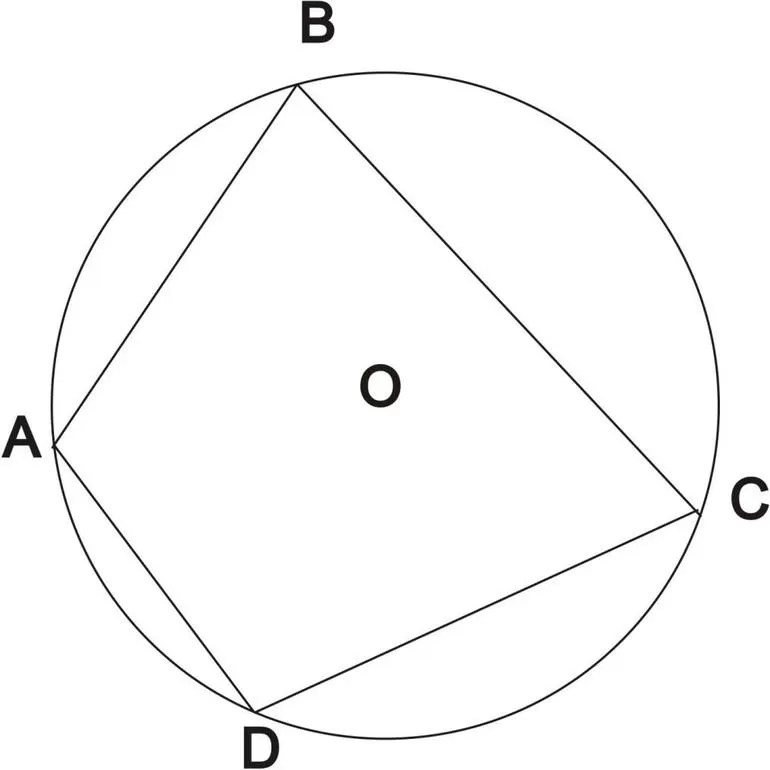
Фигура является вписанной в окружность, когда все ее вершины лежат на ней. Произвести вписание в окружность четырехугольника можно только в том случае, когда он выпуклый. Все его точки находятся по одну сторону от произвольной прямой, которая проходит через соседние вершины фигуры. Нужно отметить, что в этом случае окружность является описанной вокруг фигуры. Если в параллелограмм вписана окружность, то ее центр совпадает с центром окружности, которая описана вокруг него.
Четырехугольники бывают самопересекающимися. Они также могут быть вписанными, однако это встречается крайне редко. Не каждую фигуру можно вписать в круг, поскольку существуют определенные законы. Например, вокруг ромба нельзя описать круг — исключение составляет случай, когда ромб является квадратом.
Основные правила
Выпуклый четырехугольник можно вписать в окружность. Однако для этого существуют некоторые правила (критерии) или признаки. Некоторые задачи сформулированы таким образом, что нужно знать основные критерии, а также уметь доказывать возможность вписывать или описывать окружность. Около четырехугольника можно описать окружность, если выполняются следующие условия:
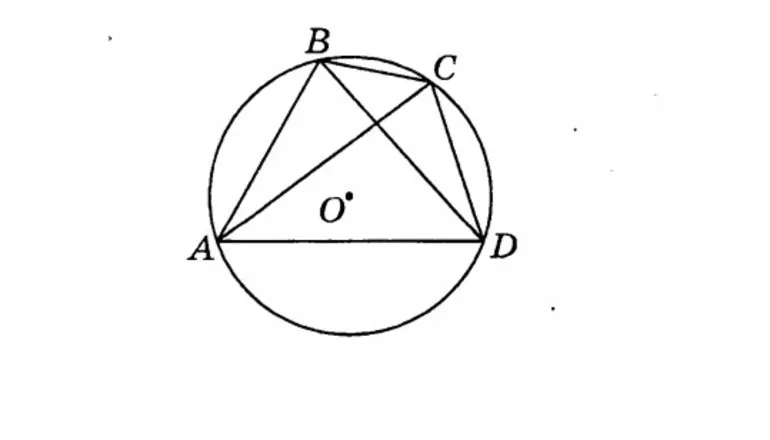
- Сумма углов, которые являются противоположными, соответствует 180 градусам.
- Соблюдается равенство смежного и противоположного углов.
- Угол между стороной и диагональю равен углу между противоположной стороной и диагональю.
- Произведение двух диагоналей соответствует размерности суммы произведений противоположных сторон.
- Четыре точки лежат на окружности, когда две прямые АС и BD, образующие диагонали, пересекаются в некоторой точке P, а также выполняется следующее равенство: AP * PC = BP * PD.
- Произведения тангенсов половины двух противоположных углов равны 1. Кроме того, значения произведений эквивалентны друг другу (tg (A/2) * tg (C/2) = tg (B/2) * tg (D/2) = 1).
Четвертое утверждение является теоремой Птолемея. Все эти правила являются следствиями, полученными при доказательстве различных гипотез. Правила можно применять в зависимости от условия поставленной задачи. Любой параллелограмм можно вписать в окружность, когда он является прямоугольником или квадратом.
Свойства и утверждения
При решении можно воспользоваться некоторыми свойствами, которые были доказаны. Это нужно для того, чтобы не тратить время на выведение какой-либо формулы. Применяется методика для оптимизации вычислений. К ним можно отнести следующие:
- Если вокруг четырехугольника описана окружность, то центры окружностей, которые вписанных в треугольники, образованные диагоналями фигуры, являются вершинами прямоугольника.
- Не бывает четырехугольников, вписанных в окружность, с рациональной площадью и сторонами, которые образуют арифметический или геометрический тип прогрессии.
- При продолжении сторон до точек пересечения Y и Z, внутренние биссектрисы углов Y и Z являются перпендикулярными.
Данные утверждения применяются не всегда. В некоторых случаях можно ограничиться формулами и основными соотношениями — они позволяют легко и быстро искать нужные величины.
Формулы и соотношения
Очень часто необходимо перерыть горы информации для поиска нужной формулы. Это сказывается на оптимизации решения. Кроме того, некоторые соотношения могут содержать ошибки, поскольку материал излагается неквалифицированными специалистами.
Педагоги утверждают, что обучение какой-либо дисциплине с физико-математическим уклоном должно быть основано на алгоритмах. Кроме того, рекомендуется прочитать условие задачи несколько раз до полного его понимания. В основном необходимо находить площадь, диагонали и углы четырехугольника.
Периметр и полупериметр

Периметром выпуклого четырехугольника со сторонами a, b, c и d называется сумма длин всех его сторон. Величина обозначается литерой «Р», и вычисляется по следующей формуле: P = a + b + c +d. Кроме того, в некоторых формулах встречается величина, которая называется полупериметром. Обозначается она литерой «р». Для ее нахождения применяется такое соотношение: p = P / 2 = (a + b + c +d) / 2. Единицей измерения полупериметра являются метрические величины: мм, см, дм, м и т. д.
Для квадрата формула периметра имеет вид: P = 4 * a. Равенство легко доказывается для фигуры со стороной а. Из определения периметра получается соотношение: P = a + a + a + a. Если привести подобные слагаемые, то результирующая формула имеет вид: P = 4 * a. У прямоугольника противоположные стороны равны. Чтобы найти его периметр, нужно воспользоваться равенством: P = a + b + a + b = 2 * (a + b). Необходимо отметить, что квадрат является правильным четырехугольником, поскольку его стороны равны между собой.
Понятие площади
Площадь двумерных фигур — понятие геометрии, которое показывает ее численную характеристику или размер. Очень часто она обозначается литерой S. Измеряется величина в квадратных единицах (см 2 , м 2 и т. д. ). Фигура, имеющая характеристику S, называется квадратируемой.
Для нахождения S применяется интегральный метод, но существуют частные случаи, при которых интегрировать необязательно. Очень часто возникает необходимость перевода одной единицы в другую. Для этого существует простой алгоритм, позволяющий корректно выполнить данную операцию. Например, нужно перевести м 2 в см 2 . Необязательно заучивать единицы площади и их эквивалентность другим. Достаточно выполнить следующие действия:
- Определить базовую единицу: м и см.
- Выполнить перевод одной метрической величины в другую: 1 м = 100 см.
- Возвести обе части выражения во втором пункте в квадрат: 1 м 2 = 100 2 см 2 = 10000 см 2 .
Однако бывают и другие единицы, которые применяются для измерения размерности земельных участков: 1 ар (сокращенно а) = 1 сотке = 100 м 2 и 1 гектар (га) = 10000 м 2.

Когда известны все стороны четырехугольника (a, b, c и d), который вписан в окружность, можно найти его S. Для этого нужно знать еще одну величину. Она называется полупериметром. Расчет выполняется по формуле: S = [(p — a) * (p — b) * (p — c) * (p — d)]^(½). Соотношение называется формулой Брахмагупты.
Необходимо отметить, что вписанный четырехугольник обладает максимальным значением S среди остальных эквивалентных фигур. Если известны четыре стороны, которые являются последовательными (a, b, c и d), а также угол В между a и b, то можно воспользоваться более упрощенной формулой: S = [(a * b + c * d) * sin (B)] / 2. В случае, когда известны все стороны и любой угол (Y) между диагоналями, соотношение можно записать таким образом: S = [(a * с + и * d) * sin (Y)] / 2.
Площадь можно выразить и другим соотношением, когда известны все стороны и угол А, который не является прямым: S = [(a 2 — b 2 — c 2 + d 2 ) * tg (A)] / 4. При известном радиусе описанной окружности и углах (A, B и Y) можно воспользоваться такой формулой: S = 2 * R^(2) * sin (A) * sin (B) * sin (Y). Следствием из последнего соотношения является S <= 2 * R 2 . Если четырехугольник является квадратом, то неравенство преобразуется в равенство, т. е. S = 2 * R 2.
Диагонали и углы

Для вписанного четырехугольника ABCD существуют определенные соотношения, по которым можно найти его диагонали. Для фигуры со сторонами a = AB, b = BC, c = CD и d = DA диагонали (s = АС и t = DA) находятся таким образом: s = [((a * c + b * d) * (a * d + b * c)) / (a * b + c * d)]^(½) и t = [((a * c + b * d) * (a * b + d * c)) / (a * d + c * b)]^(½). Если умножить диагональ s на t и привести подобные слагаемые, то в результате получится формула Птолемея: s * t = a * c + b * d.
При отношении двух диагоналей получается вторая теорема Птолемея: s / t = (a * d + b * c) / (a * b + d * c). Сумма диагоналей — есть неравенство такого вида: s + t >= 2 * [a * c + b * d]^(½). Неравенство преобразуется в равенство, когда диагонали равны. Однако в этом случае можно воспользоваться следующим выражением: [s + t]^(½) >= [a * c]^(2) + [b * d]^(2).
Необходимо отметить, что в произвольном выпуклом четырехугольнике диагонали делят его на 4 треугольника, которые являются между собой подобными по парам. Кроме того, при пересечении двух диагоналей AC и BD в некоторой точке М, справедливо следующее соотношение: AM / CM = (AB * AD) / (CB * CD).
Можно находить и некоторые углы фигуры. Для этого существуют определенные соотношения. Во вписанном четырехугольнике со сторонами, которые соответствуют значениям a, b, c и d, углом A между сторонами a и d, а также полупериметром p, функции тригонометрического типа для А вычисляются таким образом:
- cos (A) = (a 2 + d 2 — b 2 — c 2 ) / (2 * (a * d + b + c)).
- sin (A) = [(p — a) * (p — b) * (p — c) * (p — d)]^(½) / (a * d + b + c).
- tg (A/2) = [((p — a) * (p — d)) / ((p — b) * (p — c))]^(½).
В некоторых случаях нужно вычислить значение тангенса для угла Y, который находится между диагоналями, по формуле: tg (Y/2) = [((p — b) * (p — d)) / ((p — a) * (p — c))]^(½).
В геометрии существует вписанный четырехугольник, стороны которого являются целыми числами. Кроме того, целочисленными являются также его диагонали и площадь. Он называется четырехугольником Брахмагупты. Однако для преобразования любого четырехугольника в данную фигуру необходимо выполнить некоторые математические операции. Пусть он имеет следующие целочисленные параметры:
- Стороны: a, b, c и d.
- Диагонали: s и t.
- Площадь: S.
- Радиус описанной окружности: R.
В некоторых случаях возникает необходимость избавиться от рациональных значений в знаменателе. При значениях дробных параметров k, l и m нужно использовать такие соотношения:
- a = [k * (l + m) + (1 — (l * m))] * [l + m — k * (1 — (l * m))].
- b = (1 — l 2 ) * (m — k) * (1 + k * m).
- c = k * (1 + l 2 ) * (1 + m 2 ).
- d = (1 + m 2 ) * (l — k) * (1 + k * l).
- s = l * (1 + k 2 ) * (1 + m 2 ).
- t = m * (1 + k 2 ) * (1 + l 2 ).
- S = l * m * [2 * k * (1 — l * m) — (l + m) * (1 — k 2 )] * [2 * k (l + m) + (1 — l * m) * (1 — k 2 )].
- 4 * R = (1 + l 2 ) * (1 + m 2 ) * (1 + k 2 ).
Существуют также соотношения для описанной вокруг четырехугольника окружности. Математики утверждают, что при комбинации двух и более геометрических фигур время поиска некоторых параметров увеличивается.
Параметры для окружности
Радиус окружности R для четырехугольника c полупериметром р и со сторонами a, b, c, d находится по формуле Парамешвары: R = (¼) * [((a * b + c * d) * (a * c + b * d) * (a * d + b * c)) / ((p — a) * (p — b) * (p — c) * (p — d))]^(½). Соотношение было выведено в XV веке математиком из Индии Ватассери Парамешварой.
При комбинации данной формулы с соотношением Брахмагупты можно получить следующее соотношение: 4 * S * R = [(a * b + c * d) * (a * c + b * d) * (a * d + b *c)]^(½). Следует отметить, что величина S является площадью вписанного четырехугольника. Для ортогонального четырехугольника с перпендикулярными диагоналями, которые делятся на отрезки s1, s2, t1 и t2, существует некоторое соотношение, позволяющее найти диаметр окружности (D): D 2 = (s1)^2 + (s2)^2 + (t1)^2 + (t2)^2 = a 2 + c 2 = b 2 + d 2.
Радиус в этом случае находится таким образом: R = D / 2 = [(s1)^2 + (s2)^2 + (t1)^2 + (t2)^2] / 2 = [a 2 + c 2 ] / 2 = [b 2 + d 2 ] / 2. Если выполнить сложение квадратов сторон, то получится такое равенство: 8 * R = a 2 + b 2 + c 2 + d 2 . По формуле Эйлера R можно также выразить через диагонали (s и t) и расстояние v между их серединами: R = [(s 2 + t 2 + 4 * v 2 ) / 8]^(½).
Таким образом, специалисты рекомендуют на начальных этапах обучения использовать уже готовые формулы для вычисления основных параметров выпуклого четырехугольника, вписанного в окружность.
Источник
Определение 1. Окружностью, вписанной в четырёхугольник, называют окружность, которая касается касается каждой из сторон четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, описанным около окружности или описанным четырёхугольником.

Рис.1
Замечание. В настоящем разделе мы рассматриваем только выпуклые четырёхугольники.
Теорема 1. Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны.
Доказательство. Рассмотрим четырёхугольник ABCD, описанный около окружности, и обозначим буквами E, F, G, H – точки касания сторон четырёхугольника с окружностью (рис.2).

Рис.2
В силу теоремы об отрезках касательных, проведённых к окружности из одной точки, справедливы равенства
AH = AE, BF = BE, CF = CG, DH = DG,
Складывая эти равенства, получим:
AH + BF + CF + DH =
= AE + BE + CG + DG,
Поскольку
AH + BF + CF + DH =
= AD + BC,
AE + BE + CG + DG =
= AB + CD,
то справедливо равенство
AD + BC = AB + CD,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1). Если у четырёхугольника суммы длин противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.
Доказательство. Рассмотрим четырёхугольник ABCD, длины сторон которого удовлетворяют равенству
AD +BC = AB + CD,
и проведём биссектрисы углов BAD и CDA. Обозначим точку пересечения этих биссектрис буквой O, и опустим из точки O перпендикуляры OH, OE и OG на стороны AD, AB и CD соответственно (рис.3).

Рис.3
Поскольку точка O лежит на биссектрисе угла BAD, то справедливо равенство
OH = OE,
Поскольку точка O лежит на биссектрисе угла ADC, то справедливо равенство
OH = OG,
Следовательно, справедливы равенства
OH = OE = OG,
из которых вытекает, что точки H, E и G лежат на окружности с центром в точке O и радиусом OH, касающейся сторон четырёхугольника AD, AB и CD в точках H, E и G соответственно. При этом возможны два случая:
Окружность касается касается стороны BC (рис.4).

Рис.4
В этом случае четырёхугольник ABCD описан около окружности, и теорема доказана.
Окружность не касается стороны BC.
В этом случае касательная, проведенная к окружности из точки B, пересекает прямую DC в точке K, и возможны два случая:
- Точка K лежит между точками C и D (рис.5)
- Точка C лежит между точками K и D (рис.6)

Рис.5

Рис.6
Рассмотрим случай 2а и приведём его к противоречию. В этом случае в силу того, что четырёхугольник ABKD является описанным, а также по условию теоремы справедливы равенства:
Последнее равенство утверждает, что в треугольнике BKC сумма двух сторон равна третьей стороне, что противоречит неравенству треугольниканеравенству треугольниканеравенству треугольника. Полученное противоречие доказывает, что случай 2а невозможен.
Совершенно аналогичные рассуждения позволяют заключить, что случай 2b также невозможен.
Итак, возможен и реализуется лишь случай 1.
Теорема доказана.
Из доказательства теоремы 2 непосредственно вытекает
Теорема 3. Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.
В следующей таблице приводятся примеры четырёхугольников, в которые можно вписать окружность. Доказательства утверждений непосредственно вытекают из теорем 1 и 2 и предоставляются читателю в качестве несложных упражнений.
Примеры описанных четырёхугольников
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Источник
Сегодня ты узнаешь некоторые теоремы, которые помогут тебе в решении, казалось бы, сложных задач по геометрии…
Но после прочтения этой статьи они станут легкими!
Ведь ты будешь знать все об описанном четырехугольнике!
Поехали!
Посмотри – сперва нарисуем:

А теперь напишем:
Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.
А что, разве не всегда существует такая окружность? Ведь вон треугольник-то всегда является описанным – потому что во всякий треугольник можно вписать окружность. Чем же четырехугольник-то хуже? И вот оказывается, что чем-то, да хуже.
Представь себе, например, длинный прямоугольник.

Как вот в него, спрашивается, можно вписать окружность? Конечно, никак. И это лишь один из примеров четырехугольника, в которой НЕЛЬЗЯ вписать окружность.
А в какие же можно? Вот, оказывается есть такая теорема (утверждение то есть).
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
Вот как это записывается в буквах:
( displaystyle a+c=b+d)
или (то же самое)
( displaystyle AB+CD=AD+BC)
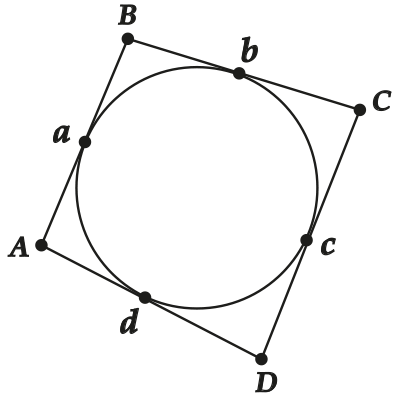
Для лучшего понимания давай в буквальном смысле разберём на кусочки описанный четырехугольник. Смотри: пусть в четырехугольнике ( displaystyle ABCD) «сидит» окружность.

Но тогда у нас есть огромное количество касательных! Ты ещё помнишь, что отрезки касательных, проведённых из одной точки, равны? Ну, вот, значит
( displaystyle BK=BN) (обозначим ( displaystyle x))
( displaystyle CK=CL) (обозначим ( displaystyle y))
( displaystyle DL=DM) (обозначим ( displaystyle z))
( displaystyle AM=AN) (обозначим ( displaystyle u))
А теперь получилось, что
( displaystyle left| begin{array}{l}AB=x+u\CD=y+zend{array} right.Rightarrow AB+CD=x+y+z+u)
и
( displaystyle left| begin{array}{l}BC=x+y\AD=u+zend{array} right.Rightarrow BC+AD=x+y+z+u)
То есть ( displaystyle AB+CD=AD+BC)! Здорово, правда?
А теперь получим простое, но красивое следствие из этой теоремы.
Следствие.Если в параллелограмм можно вписать окружность, то это ромб.
Почему? Давай разберёмся. Пусть есть параллелограмм ( displaystyle ABCD).
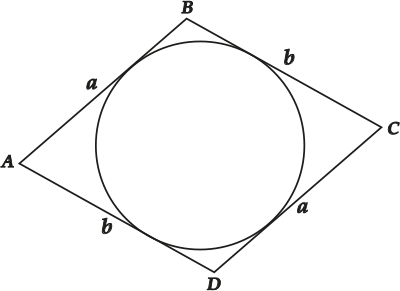
Раз параллелограмм, то ( displaystyle AB=CD,~AD=BC) (вспоминаем свойства параллелограмма). Обозначим ( displaystyle text{AB}=text{CD}) буквой ( displaystyle a), а ( displaystyle text{AD}=text{BC}) буквой ( displaystyle b).
А теперь применим теорему. ( displaystyle ABCD) описанный ( displaystyle Rightarrow a+a=b+b), то есть ( displaystyle a=b) – вот и получился ромб.

Видишь, как сработала теорема?
Вот и ты, если видишь в задачке надпись «в четырёхугольник вписана окружность» или, конкретнее, скажем, «в трапецию вписана окружность», то сразу вспоминай, что ( displaystyle AB+CD=AD+BC), – и задача решится!
Ну… или не сразу решится, но этот факт непременно тебе поможет.

Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.
Давай прежде всего осознаем, что, в отличие от треугольника, далеко не во всякий четырехугольник можно поместить окружность так, чтобы она касалась всех его сторон.
Ну, вот пример:

А раз так, то математики, конечно же, не могли успокоиться, пока не придумали теорему, которая сообщит нам, что же такое нужно требовать от четырехугольника, чтобы в него можно было поместить окружность, касающуюся всех сторон.
И вот эта теорема:
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
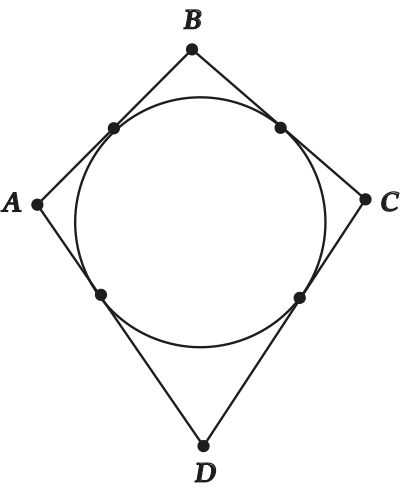
В буквах:
( large a+c=b+d)
или (в других буквах)
( large AB+CD=AD+BC)
Заметь, что (как всегда) слова «тогда и только тогда» означают сразу два утверждения: «туда» и «обратно». Итак, если подробнее, то теорема утверждает
1
Если в четырехугольник можно вписать окружность, то ( AB+CD=AD+BC)
2
Если в четырехугольнике есть ( AB+CD=AD+BC), то в него можно вписать окружность.
(Вспоминаем Алису с безумным шляпником и их «ем то, что вижу» и «вижу то, что ем»)
А теперь – доказательство!
Пункт 1 вообще ОЧЕНЬ лёгкий. Смотри:

Пусть в ( ABCD) вписана окружность. Тогда получается из точек ( A,B,C,) и ( D) проведено по две касательных, которые равны!
(Вспоминаем о равенстве отрезков касательных проведённых из одной точки)
Итак, у нас
( displaystyle BK=BN) (обозначим ( x))
( displaystyle CK=CL) (обозначим ( y))
( displaystyle DL=DM) (обозначим ( z))
( displaystyle AM=AN) (обозначим ( u))
И теперь получается, что
( begin{array}{*{20}{c}}{AB = x + u}\{CD = y + z}end{array} Rightarrow AB + CD = x + y + z + u)
и
( begin{array}{*{20}{c}}{BC = x + u}\{AD = u + z}end{array} Rightarrow AD + BC = x + y + z + u)
( displaystyle Rightarrow AB+CD=AD+BC!)
Обе этих суммы состоят из одинаковых кусочков, просто взятых в разном порядке.
Готово: пункт 1 доказали.
А теперь, наоборот, пункт 2.
Пусть в ( displaystyle ABCD) выполняется ( displaystyle AB+CD=AD+BC)
Чтобы что-то понять, впишем окружность сперва в такую «кастрюлю» – ( displaystyle ABCD) без стороны ( displaystyle AD).
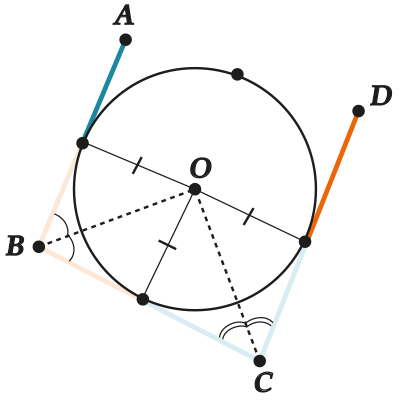
Обрати внимание, что это всегда можно сделать – центром ( displaystyle O) такой окружности будет пересечение биссектрис углов ( displaystyle B) и ( displaystyle C).
Ну вот, в «кастрюле» сидит окружность. При этом сторона ( displaystyle AD), если она НЕ касается этой окружности, может либо пересекать её, либо вовсе не иметь с ней общих точек.
Разберём эти случаи и убедимся, что оба они ведут к противоречию.
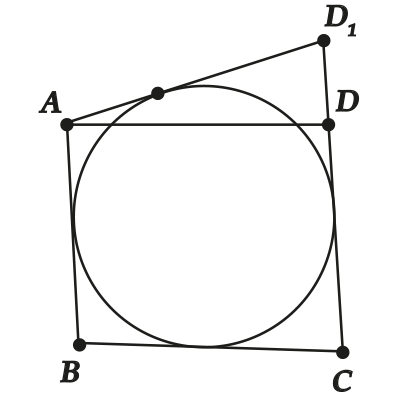
Пусть ( displaystyle AD) пересекает окружность. Давай тогда проведём ( displaystyle A{{D}_{1}}), которая будет касаться окружности.
По пункту 1 для четырехугольника ( displaystyle ABC{{D}_{1}}) должно быть
( displaystyle AB+C{{D}_{1}}=A{{D}_{1}}+BC),
а по условию для четырехугольника ( displaystyle ABCD)
( displaystyle AB+CD=AD+BC).
Значит (вычитаем нижнее равенство из верхнего)
( displaystyle C{{D}_{1}}-CD=A{{D}_{1}}-AD)
То есть ( displaystyle D{{D}_{1}}+AD=A{{D}_{1}})
Но так СОВСЕМ не может быть – нарушается неравенство треугольника для ( Delta AD{{D}_{1}}):
должно быть ( D{{D}_{1}}+AD>A{{D}_{1}}), а у нас ( D{{D}_{1}}+AD=A{{D}_{1}}).
Вот и противоречие. Поэтому точно выяснили, что ( AD) НЕ МОЖЕТ пересекать окружность.
Пусть теперь ( AD) «не дотягивается» до окружности.
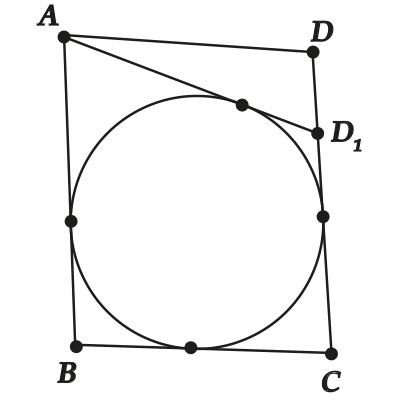
Снова проведём ( A{{D}_{1}}), которая этой окружности каснется.
И опять ( AB+C{{D}_{1}}=A{{D}_{1}}+BC) и ( AB+CD=AD+BC).
Теперь вычитаем из нижнего верхнее.
( CD-C{{D}_{1}}=AD-A{{D}_{1}})
То есть ( displaystyle D{{D}_{1}}+A{{D}_{1}}=AD) – опять нарушаем неравенство треугольника для ( displaystyle Delta AD{{D}_{1}}) – значит, опять имеем противоречие и заключаем, что ( displaystyle AD) НЕ МОЖЕТ вовсе не иметь общих точек с окружностью.
И что же этой бедной ( displaystyle AD) остаётся?
Только касаться окружности.
Вот и доказали пункт 2, а с ним и всю теорему.
А теперь посмотрим, как работает эта теорема. Докажем следующее следствие из теоремы.
Следствие. Если в параллелограмм можно вписать окружность, то это – ромб.
Доказываем: пусть есть параллелограмм ( displaystyle ABC{{D}}).
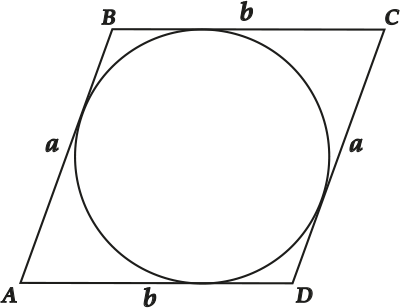
По свойству параллелограмма ( displaystyle AB=CD~) (обозначим ( displaystyle a)) и ( displaystyle BC=AD~) (обозначим ( displaystyle b)).
Раз в ( displaystyle ABCD) можно вписать окружность, то ( displaystyle AB+CD=AD+BC), то есть ( displaystyle 2a=2b); ( displaystyle a=b).
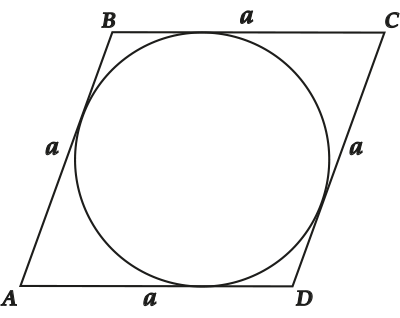
Вот и получился ромб. Понравилось?
Вот и прими на вооружение: если в задаче сказано, что окружность вписана в какой-нибудь четырехугольник, то постарайся применить то, что тогда ( displaystyle AB+CD=AD+BC) или даже прямо структуру из кусочков касательных – обязательно поможет!
Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.

- В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. В буквах: ( large AB+CD=AD+BC)

- Если в параллелограмм можно вписать окружность, то это – ромб.
P.S. Последний бесценный совет ????
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
- проверить свою готовность к каждому типу задач на ЕГЭ (пройдя тест);
- подтянуть слабые места с помощью видеоуроков, вебинаров;
- понять тему с помощью статей учебника YouClever;
- набить руку, решая задачи и получая проверку и решения;
- сдать пробный ЕГЭ и получить сра?
