Какими свойствами обладает четырехугольник около которого описана окружность

Сегодня ты узнаешь некоторые теоремы, которые помогут тебе в решении, казалось бы, сложных задач по геометрии…
Но после прочтения этой статьи они станут легкими!
Ведь ты будешь знать все об описанном четырехугольнике!
Поехали!
Посмотри – сперва нарисуем:

А теперь напишем:
Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.
А что, разве не всегда существует такая окружность? Ведь вон треугольник-то всегда является описанным – потому что во всякий треугольник можно вписать окружность. Чем же четырехугольник-то хуже? И вот оказывается, что чем-то, да хуже.
Представь себе, например, длинный прямоугольник.

Как вот в него, спрашивается, можно вписать окружность? Конечно, никак. И это лишь один из примеров четырехугольника, в которой НЕЛЬЗЯ вписать окружность.
А в какие же можно? Вот, оказывается есть такая теорема (утверждение то есть).
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
Вот как это записывается в буквах:
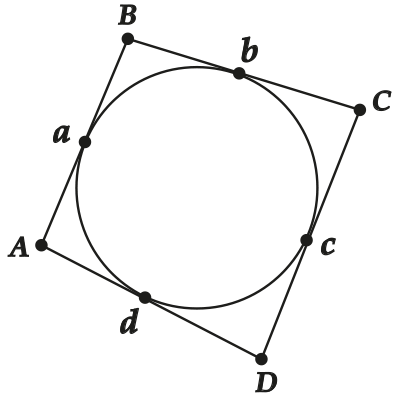
( displaystyle a+c=b+d)
или (то же самое)
( displaystyle AB+CD=AD+BC)
Для лучшего понимания давай в буквальном смысле разберём на кусочки описанный четырехугольник. Смотри: пусть в четырехугольнике ( displaystyle ABCD) «сидит» окружность.

Но тогда у нас есть огромное количество касательных! Ты ещё помнишь, что отрезки касательных, проведённых из одной точки, равны? Ну, вот, значит
( displaystyle BK=BN) (обозначим ( displaystyle x))
( displaystyle CK=CL) (обозначим ( displaystyle y))
( displaystyle DL=DM) (обозначим ( displaystyle z))
( displaystyle AM=AN) (обозначим ( displaystyle u))
А теперь получилось, что
( displaystyle left| begin{array}{l}AB=x+u\CD=y+zend{array} right.Rightarrow AB+CD=x+y+z+u)
и
( displaystyle left| begin{array}{l}BC=x+y\AD=u+zend{array} right.Rightarrow BC+AD=x+y+z+u)
То есть ( displaystyle AB+CD=AD+BC)! Здорово, правда?
А теперь получим простое, но красивое следствие из этой теоремы.
Следствие.Если в параллелограмм можно вписать окружность, то это ромб.
Почему? Давай разберёмся. Пусть есть параллелограмм ( displaystyle ABCD).
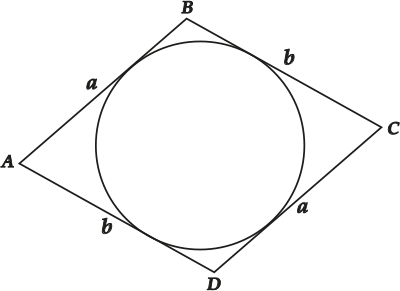
Раз параллелограмм, то ( displaystyle AB=CD,~AD=BC) (вспоминаем свойства параллелограмма). Обозначим ( displaystyle text{AB}=text{CD}) буквой ( displaystyle a), а ( displaystyle text{AD}=text{BC}) буквой ( displaystyle b).
А теперь применим теорему. ( displaystyle ABCD) описанный ( displaystyle Rightarrow a+a=b+b), то есть ( displaystyle a=b) – вот и получился ромб.

Видишь, как сработала теорема?
Вот и ты, если видишь в задачке надпись «в четырёхугольник вписана окружность» или, конкретнее, скажем, «в трапецию вписана окружность», то сразу вспоминай, что ( displaystyle AB+CD=AD+BC), – и задача решится!
Ну… или не сразу решится, но этот факт непременно тебе поможет.

Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.
Давай прежде всего осознаем, что, в отличие от треугольника, далеко не во всякий четырехугольник можно поместить окружность так, чтобы она касалась всех его сторон.
Ну, вот пример:

А раз так, то математики, конечно же, не могли успокоиться, пока не придумали теорему, которая сообщит нам, что же такое нужно требовать от четырехугольника, чтобы в него можно было поместить окружность, касающуюся всех сторон.
И вот эта теорема:
В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
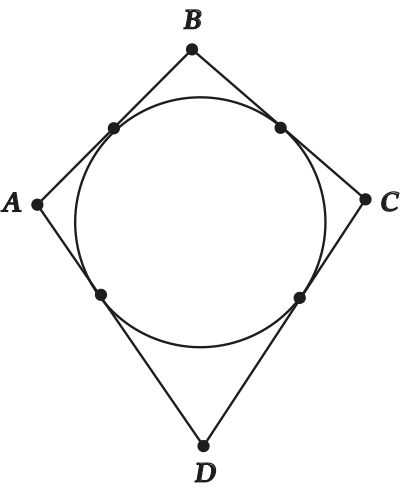
В буквах:
( large a+c=b+d)
или (в других буквах)
( large AB+CD=AD+BC)
Заметь, что (как всегда) слова «тогда и только тогда» означают сразу два утверждения: «туда» и «обратно». Итак, если подробнее, то теорема утверждает
1
Если в четырехугольник можно вписать окружность, то ( AB+CD=AD+BC)
2
Если в четырехугольнике есть ( AB+CD=AD+BC), то в него можно вписать окружность.
(Вспоминаем Алису с безумным шляпником и их «ем то, что вижу» и «вижу то, что ем»)
А теперь – доказательство!
Пункт 1 вообще ОЧЕНЬ лёгкий. Смотри:

Пусть в ( ABCD) вписана окружность. Тогда получается из точек ( A,B,C,) и ( D) проведено по две касательных, которые равны!
(Вспоминаем о равенстве отрезков касательных проведённых из одной точки)
Итак, у нас
( displaystyle BK=BN) (обозначим ( x))
( displaystyle CK=CL) (обозначим ( y))
( displaystyle DL=DM) (обозначим ( z))
( displaystyle AM=AN) (обозначим ( u))
И теперь получается, что
( begin{array}{*{20}{c}}{AB = x + u}\{CD = y + z}end{array} Rightarrow AB + CD = x + y + z + u)
и
( begin{array}{*{20}{c}}{BC = x + u}\{AD = u + z}end{array} Rightarrow AD + BC = x + y + z + u)
( displaystyle Rightarrow AB+CD=AD+BC!)
Обе этих суммы состоят из одинаковых кусочков, просто взятых в разном порядке.
Готово: пункт 1 доказали.
А теперь, наоборот, пункт 2.
Пусть в ( displaystyle ABCD) выполняется ( displaystyle AB+CD=AD+BC)
Чтобы что-то понять, впишем окружность сперва в такую «кастрюлю» – ( displaystyle ABCD) без стороны ( displaystyle AD).
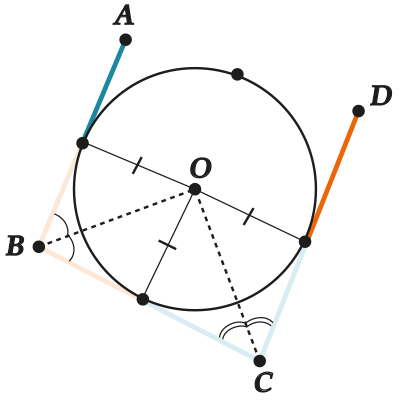
Обрати внимание, что это всегда можно сделать – центром ( displaystyle O) такой окружности будет пересечение биссектрис углов ( displaystyle B) и ( displaystyle C).
Ну вот, в «кастрюле» сидит окружность. При этом сторона ( displaystyle AD), если она НЕ касается этой окружности, может либо пересекать её, либо вовсе не иметь с ней общих точек.
Разберём эти случаи и убедимся, что оба они ведут к противоречию.
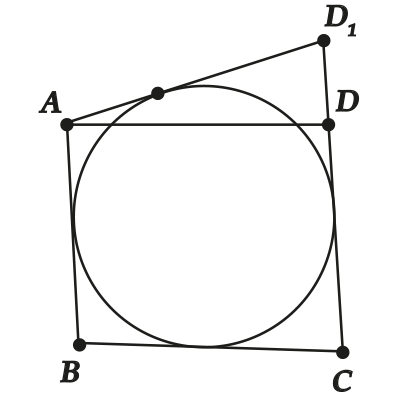
Пусть ( displaystyle AD) пересекает окружность. Давай тогда проведём ( displaystyle A{{D}_{1}}), которая будет касаться окружности.
По пункту 1 для четырехугольника ( displaystyle ABC{{D}_{1}}) должно быть
( displaystyle AB+C{{D}_{1}}=A{{D}_{1}}+BC),
а по условию для четырехугольника ( displaystyle ABCD)
( displaystyle AB+CD=AD+BC).
Значит (вычитаем нижнее равенство из верхнего)
( displaystyle C{{D}_{1}}-CD=A{{D}_{1}}-AD)
То есть ( displaystyle D{{D}_{1}}+AD=A{{D}_{1}})
Но так СОВСЕМ не может быть – нарушается неравенство треугольника для ( Delta AD{{D}_{1}}):
должно быть ( D{{D}_{1}}+AD>A{{D}_{1}}), а у нас ( D{{D}_{1}}+AD=A{{D}_{1}}).
Вот и противоречие. Поэтому точно выяснили, что ( AD) НЕ МОЖЕТ пересекать окружность.
Пусть теперь ( AD) «не дотягивается» до окружности.
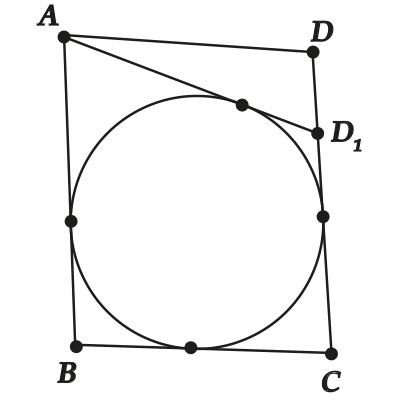
Снова проведём ( A{{D}_{1}}), которая этой окружности каснется.
И опять ( AB+C{{D}_{1}}=A{{D}_{1}}+BC) и ( AB+CD=AD+BC).
Теперь вычитаем из нижнего верхнее.
( CD-C{{D}_{1}}=AD-A{{D}_{1}})
То есть ( displaystyle D{{D}_{1}}+A{{D}_{1}}=AD) – опять нарушаем неравенство треугольника для ( displaystyle Delta AD{{D}_{1}}) – значит, опять имеем противоречие и заключаем, что ( displaystyle AD) НЕ МОЖЕТ вовсе не иметь общих точек с окружностью.
И что же этой бедной ( displaystyle AD) остаётся?
Только касаться окружности.
Вот и доказали пункт 2, а с ним и всю теорему.
А теперь посмотрим, как работает эта теорема. Докажем следующее следствие из теоремы.
Следствие. Если в параллелограмм можно вписать окружность, то это – ромб.
Доказываем: пусть есть параллелограмм ( displaystyle ABC{{D}}).
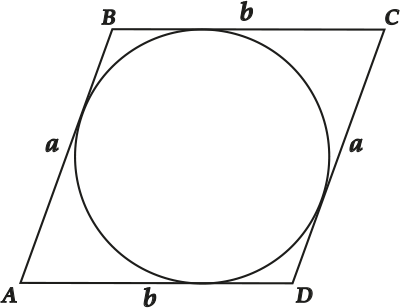
По свойству параллелограмма ( displaystyle AB=CD~) (обозначим ( displaystyle a)) и ( displaystyle BC=AD~) (обозначим ( displaystyle b)).
Раз в ( displaystyle ABCD) можно вписать окружность, то ( displaystyle AB+CD=AD+BC), то есть ( displaystyle 2a=2b); ( displaystyle a=b).
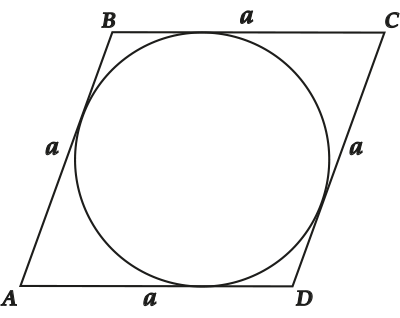
Вот и получился ромб. Понравилось?
Вот и прими на вооружение: если в задаче сказано, что окружность вписана в какой-нибудь четырехугольник, то постарайся применить то, что тогда ( displaystyle AB+CD=AD+BC) или даже прямо структуру из кусочков касательных – обязательно поможет!
Четырехугольник называется описанным, если существует окружность, касающаяся всех его сторон.

- В четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны. В буквах: ( large AB+CD=AD+BC)

- Если в параллелограмм можно вписать окружность, то это – ромб.
P.S. Последний бесценный совет ????
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
- проверить свою готовность к каждому типу задач на ЕГЭ (пройдя тест);
- подтянуть слабые места с помощью видеоуроков, вебинаров;
- понять тему с помощью статей учебника YouClever;
- набить руку, решая задачи и получая проверку и решения;
- сдать пробный ЕГЭ и получить сразу оценку и разбор ошибок.
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Расскажи нам…
Описанные четырехугольники – легкотня, не так ли?
Выглядит странно, но на деле это довольно просто и полезно. Особенно часто помощь от них придет в задачах на трапецию.
Мы будем очень рады услышать твое мнение об этой статье! Как тебе? Понравилось? ????
Все ли было понятно?
Напиши в комментариях внизу!
И еще можешь задать любые вопросы, если такие есть!
Мы обязательно ответим.
Удачи!
Источник
Определение 1. Окружностью, вписанной в четырёхугольник, называют окружность, которая касается касается каждой из сторон четырёхугольника (рис.1). В этом случае четырёхугольник называют четырёхугольником, описанным около окружности или описанным четырёхугольником.

Рис.1
Замечание. В настоящем разделе мы рассматриваем только выпуклые четырёхугольники.
Теорема 1. Если четырёхугольник описан около окружности, то суммы длин его противоположных сторон равны.
Доказательство. Рассмотрим четырёхугольник ABCD, описанный около окружности, и обозначим буквами E, F, G, H – точки касания сторон четырёхугольника с окружностью (рис.2).

Рис.2
В силу теоремы об отрезках касательных, проведённых к окружности из одной точки, справедливы равенства
AH = AE, BF = BE, CF = CG, DH = DG,
Складывая эти равенства, получим:
AH + BF + CF + DH =
= AE + BE + CG + DG,
Поскольку
AH + BF + CF + DH =
= AD + BC,
AE + BE + CG + DG =
= AB + CD,
то справедливо равенство
AD + BC = AB + CD,
что и требовалось доказать.
Теорема 2 (обратная теорема к теореме 1). Если у четырёхугольника суммы длин противоположных сторон равны, то в этот четырёхугольник можно вписать окружность.
Доказательство. Рассмотрим четырёхугольник ABCD, длины сторон которого удовлетворяют равенству
AD +BC = AB + CD,
и проведём биссектрисы углов BAD и CDA. Обозначим точку пересечения этих биссектрис буквой O, и опустим из точки O перпендикуляры OH, OE и OG на стороны AD, AB и CD соответственно (рис.3).

Рис.3
Поскольку точка O лежит на биссектрисе угла BAD, то справедливо равенство
OH = OE,
Поскольку точка O лежит на биссектрисе угла ADC, то справедливо равенство
OH = OG,
Следовательно, справедливы равенства
OH = OE = OG,
из которых вытекает, что точки H, E и G лежат на окружности с центром в точке O и радиусом OH, касающейся сторон четырёхугольника AD, AB и CD в точках H, E и G соответственно. При этом возможны два случая:
Окружность касается касается стороны BC (рис.4).

Рис.4
В этом случае четырёхугольник ABCD описан около окружности, и теорема доказана.
Окружность не касается стороны BC.
В этом случае касательная, проведенная к окружности из точки B, пересекает прямую DC в точке K, и возможны два случая:
- Точка K лежит между точками C и D (рис.5)
- Точка C лежит между точками K и D (рис.6)

Рис.5

Рис.6
Рассмотрим случай 2а и приведём его к противоречию. В этом случае в силу того, что четырёхугольник ABKD является описанным, а также по условию теоремы справедливы равенства:
Последнее равенство утверждает, что в треугольнике BKC сумма двух сторон равна третьей стороне, что противоречит неравенству треугольниканеравенству треугольниканеравенству треугольника. Полученное противоречие доказывает, что случай 2а невозможен.
Совершенно аналогичные рассуждения позволяют заключить, что случай 2b также невозможен.
Итак, возможен и реализуется лишь случай 1.
Теорема доказана.
Из доказательства теоремы 2 непосредственно вытекает
Теорема 3. Биссектрисы всех внутренних углов описанного четырёхугольника пересекаются в одной точке – центре вписанной окружности.
В следующей таблице приводятся примеры четырёхугольников, в которые можно вписать окружность. Доказательства утверждений непосредственно вытекают из теорем 1 и 2 и предоставляются читателю в качестве несложных упражнений.
Примеры описанных четырёхугольников
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Источник
Анонимный вопрос
16 мая 2018 · < 100
Как узнать, проходимы ли маточные трубы?
Группа клиник “Альтермед” работает в Санкт-Петербурге с 1999 года. За это время мы… · altermed.ru
КМН, врач гинеколог-эндокринолог, репродуктолог, специалист УЗД, заведующая отделением гинекологии в группе клиник «Альтермед»
В настоящее время существует 3 метода диагностики проходимости маточных труб. Все они требуют предварительного обследование: мазок на степень чистоты влагалища, онкоцитологический мазок, кровь на спид гепатиты В и С и сифилис. При выявлении воспаления во влагалище необходимо обследование на инфекции и соответствующее лечение.
- Ультразвуковая гистерсальпингоскопия. Проводится при помощи УЗ аппарата. В шейке матки устанавливается стерильный катетер, через который в полость матки вводиться стерильный физиологический раствор. В последующем на экране УЗ аппарата отслеживается движение жидкости по полости матки и трубам, а также оценивается количество жидкости, скопившееся в брюшной полости. Метод безопасный, безболезненный, не требует предварительной подготовки, результат выдаётся на руки по окончании процедуры.
- Гистеросальпингография (ГСГ) делаются рентгенологические снимки. В полость матки водиться рентгеноконтрастный препарат, продвижения которого и фиксируется на рентгенологических снимках. В течение нескольких минут жидкость должна заполнить полость матки, пройти по трубам и излиться в брюшную полость. За этот период времени делаются серия снимков. При здоровых трубах на снимках видна 3-х угольная форма матки, извитая линия просвета маточных труб с двух сторон и гиперэхогенное «пятно» ретгеноконтрастной жидкости, вытекшей из полости матки через трубы в полость живота.
- Лапароскопическая операция проводится в стационаре. Требует предварительного полного клинического обследования. Госпитализацию в больницу на несколько суток. Проводится под общим наркозом. Через отверстия в передней брюшной стенке в полость живота вводится инструмент (камера), который позволяет визуально осмотреть матку, яичники, маточные трубы. Лапароскопия позволяет не только оценить состояние маточных труб, но и при необходимости провести лечебные манипуляции: иссечения спаек (основная причина непроходимости труб), разъединить слипшиеся концы маточных труб, тем самым восстановить проходимость трубы. Таким образом, лапароскопия носит диагностически – лечебный характер. В большинстве случаях к лапароскопии прибегают при неблагоприятных или сомнительных результатах УЗГСС и ГСГ
Более подробно можно узнать здесь https://www.altermed.ru/gynecology/
Прочитать ещё 4 ответа
Возможен ли не прямоугольный треугольник, в котором сумма квадратов двух сторон равна квадрату третьей стороны?
Я согласен с ответом от Uwe Boll, но постараюсь ответить более детально.
Вообще, если вам даны один угол и длина двух сторон, или два угла и длина одной стороны, или все три стороны, то они определяют остальные три элемента. Однако если вам даны три угла, то они определяют длину сторон с точностью до фактора.
В вашем вопросе, даны длины всех трех сторон с точностью до фактора:
fA, fB, и fC=f sqrt(A^2+B^2). Мы хотим понять почему никакой “гибкости” в этом треугольнике нет.
Обозначим углы напротив каждой из сторон соотвенственно a, b, c .
Мы используем закон косинусов на плоскости:
Косинус угла напротив “длинной” стороны (мы подозреваем, гипотенузы) определен
cos(c) = (A^2 + B^2 – C^2) / (2AB)
(фактор f сокращается). (Заметим, что два других угла тоже определены без всякой гибкости, но нам они не интересны.) Дальже идет алгебра – мы знаем длину C(A,B) и подставляем в правую сторону:
(A^2 + B^2 – C^2) / (2AB) = (A^2 + B^2 – sqrt(A^2+B^2)^2) / (2AB) = (A^2 + B^2 – (A^2+B^2)) / (2AB) = 0.
То есть косинус угла c = ноль. Значит это должен быть прямой угол.
Однако закон косинусов так не работает, если ваш треугольник не на плоскости, а, например, на сфере.
Прочитать ещё 2 ответа
По какой формуле находят длину окружности?
Если женщина внезапно замолкла, значит, она хочет что-то сказать
Чтобы вычислить длину окружности, нужно знать радиус или диаметр окружности.
Умножаем диаметр окружности на число пи и получаем длину окружности.
Либо умножаем радиус на два и на число пи и опять таки получаем длину окружности.
Источник
Внимание! Предварительный просмотр слайдов используется исключительно в ознакомительных целях и может не давать представления о всех возможностях презентации. Если вас заинтересовала данная работа, пожалуйста, загрузите полную версию.
Цели.
Образовательная. Создание условий для
успешного усвоения понятия описанного
четырёхугольника, его свойства, признака и
овладения умениями применять их на практике.
Развивающая. Развитие математических
способностей, создание условий для умения
обобщать и применять прямой и обратный ход
мыслей.
Воспитательная. Воспитание чувства
красоты эстетикой чертежей, удивления необычным
решением, формирование организованности,
ответственность за результаты своего труда.
Задачи.
1. Изучить определение описанного
четырёхугольника.
2. Доказать свойство сторон описанного
четырёхугольника.
3. Познакомить с двойственностью свойств сумм
противоположных сторон и противоположных углов
вписанного и описанного четырёхугольников.
4. Дать опыт практического применения
рассмотренных теорем при решении задач.
5. Провести первичный контроль уровня усвоения
нового материала.
Оборудование:
- компьютер, проектор;
- учебник “Геометрия. 10-11 классы” для
общеобразоват. учреждений: базовый и профил.
уровни авт. А.В. Погорелов.
Программные средства: Microsoft Word, Microsoft Power Point.
Использование компьютера при подготовке
учителя к уроку.
С помощью стандартной программы операционной
системы Windows созданы к уроку:
- Презентация.
- Таблицы.
- Чертежи.
- Раздаточный материал.
План урока
Ход урока
1. Организационный момент. Приветствие.
Сообщение темы и цели урока. Запись в тетради
даты и темы урока.
2. Проверка домашнего задания.
3. Изучение нового материала.
Работа над понятием описанного
многоугольника.
Определение. Многоугольник называется описанным
около окружности, если все его стороны касаются
некоторой окружности.
Вопрос. Какие из предложенных многоугольников
являются описанными, а какие не являются и
почему?
<Презентация. Слайд №2>
Ответ.
| Нарушение “касаются” | Рисунки 1 и 2 |
| Нарушение “все стороны” | Рисунки 2 и 3 |
| Нарушение “многоугольник” | Рисунок 6 |
| Нарушение “некоторой окружности” | Рисунок 5 и 7 |
Доказательство свойств описанного
четырёхугольника.
<Презентация. Слайд №3>
Теорема. В описанном четырёхугольнике суммы
противоположных сторон равны.
Учащиеся работают с учебником, записывают
формулировку теоремы в тетрадь.
Вопросы.
1. Представить формулировку теоремы в форме
условного предложения.
2. Каково условие теоремы?
3. Каково заключение теоремы?
Ответ. Если четырёхугольник описан около
окружности, то суммы противолежащих сторон
равны.
Проводится доказательство, учащиеся делают
записи в тетради.
<Презентация. Слайд №4>
Учитель. Отметим двойственность
ситуаций для сторон и углов описанного и
вписанного четырёхугольников.
Закрепление полученных знаний.
Задачи.
четырёхугольника 8 м и 12 м . Можно ли найти
периметр?
Слайд №5>
Ответ. 1.10 м. 2. 20 м. 3. 21 м
Доказательство признака описанного
четырёхугольника.
Сформулировать обратную теорему.
Ответ. Если в четырёхугольнике суммы
противоположных сторон равны, то в него можно
вписать окружность. (Вернуться к слайду 2, рис.7)<Презентация. Слайд №2>
Учитель.Уточните формулировку теоремы.
Теорема. Если суммы противоположных сторон выпуклого
четырёхугольника равны, то в него можно вписать
окружность.
Работа с учебником. Познакомиться с
доказательством признака описанного
четырёхугольника по учебнику.
Применение полученных знаний.
3. Задачи по готовым чертежам.
1. Можно ли вписать окружность в
четырёхугольник с противоположными сторонами 9 м
и 4 м , 10 м и 3 м?
2. Можно ли вписать окружность в равнобокую
трапецию с основаниями 1 м и 9 м, высотой 3 м?
<Презентация. Слайд №6>
Письменная работа в тетрадях
.
Задача. Найти радиус окружности, вписанной
в ромб с диагоналями 6 м и 8 м.
<Презентация. Слайд № 7>
4. Самостоятельная работа.
<Приложение 2>
1 вариант
1. Можно ли вписать окружность
1) в прямоугольник со сторонами 7 м и 10 м,
2) в ромб?
2. Противоположные стороны четырёхугольника,
описанного около окружности, равны 7 м и 10 м.
Найти периметр четырёхугольника.
3. Равнобокая трапеция с основаниями 4 м и 16 м
описана около окружности.
Найти:
1) радиус вписанной окружности,
2) радиус описанной окружности.
2 вариант
1. Можно ли вписать окружность:
1) в параллелограмм со сторонами 6 м и 13 м,
2) в квадрат?
2. Противоположные стороны четырёхугольника,
описанного около окружности, равны 9 м и 11 м. Найти
периметр четырёхугольника.
3. Равнобокая трапеция с боковой стороной 5 м
описана около окружности с радиусом 2 м.
Найти:
1) основание трапеции,
2) радиус описанной окружности.
5. Домашнее задание. П.86, № 28, 29, 30.
6. Итог урока. Проверяется самостоятельная
работа, выставляются оценки.
<Презентация. Слайд № 8>
Источник
