Какими свойствами характеризуется объект математика
Беседа 4. Математические объекты
Чтобы ответить на вопрос, чему учиться в математике, надо разобраться в том, что она – математика – собой представляет, в чем ее особенности, что и как она изучает и из каких элементов (объектов) она состоит. Конечно, все эти вопросы очень сложные, и мы подробно в них разобраться не сумеем, но получить хотя бы некоторое представление обо всем этом нам необходимо, ибо иначе просто невозможно решить, чему же учиться в математике.
Математика, как и другие науки, изучает окружающий нас мир, природные и общественные явления, но изучает лишь особые стороны этих явлений.
Представьте себе, что нужно рассчитать, сколько надо купить краски, чтобы покрасить потолок комнаты, если известно, что на окраску 1 м2 уходит 120 г краски, или сколько нужно купить кафельных плиток для облицовки стены, если известно, что плитка имеет форму квадрата со стороной 15 см. Во всех этих случаях совершенно безразлично, какого цвета этот потолок или стена, из какого материала они построены и т. д. Важно лишь знать их форму и размеры. В этом случае говорят, что мы отвлекаемся (абстрагируемся) от всех свойств рассматриваемого предмета и выделяем лишь его форму и размер. В результате такого абстрагирования получаем математический объект – геометрическую фигуру.
В других случаях, кроме формы и размера, учитывают еще взаимное расположение частей фигуры.
Такие математические объекты, как числа, образуются путем выделения при рассмотрении различных совокупностей (множеств) однородных предметов таких общих свойств, как количество предметов в совокупности или их порядок следования, абстрагируясь от всех других свойств этих предметов (их неодинаковости, материала, цвета, величины и т. д.).
Вообще любые математические объекты – это результат выделения из предметов и явлений окружающего мира особых количественных и пространственных свойств и отношений и абстрагирования от всех других свойств. Следовательно, математические объекты реально не существуют, нет в окружающем нас мире геометрических точек, фигур, чисел и т. д. Все они созданы человеческим умом в процессе исторического развития людей и существуют лишь в мышлении человека и в тех знаках и символах, которые образуют математический язык. Поэтому говорят, что математические объекты – это идеальные объекты, отражающие (описывающие) реальные объекты.
Обратите внимание еще на одну особенность математических объектов. При их образовании мы не только отвлекаемся от многих свойств соответствующих предметов, но и приписываем им такие свойства, которыми никакие реальные предметы не обладают. Так, например, образуя такой математический объект, как прямая линия, мы в соответствующих предметах (край линейки, стола, луч света, нить и т. д.) не только абстрагируемся от всех их свойств, кроме свойства протяженности, но и приписываем такое свойство, как неограниченная протяженность в обоих направлениях, хотя никакой из указанных реальных предметов таким свойством не обладает. Точно так же никакая совокупность реальных предметов не является бесконечной, а вот множество натуральных чисел бесконечное, или никакой предмет не является бесконечно раздробленным, а вот число – размер этого предмета, мы считаем бесконечно раздробляемым, т. е. число можно делить на какое угодно большое число частей, и т. д.
Итак, математика изучает особые идеальные математические объекты, которые образуются путем сложной мыслительной деятельности людей в процессе познания количественных свойств и отношений, а также пространственных свойств и форм предметов и явлений окружающего мира.
Поэтому первое, чему надо учиться в математике,- это умению в процессе изучения каких-то предметов или явлений для решения задач по определению количественной стороны или пространственных соотношений этих предметов или явлений образовывать, создавать математические объекты. Рассмотрим в качестве примера такую задачу.
Задача.Для того чтобы укрепить железную дымовую трубу, было решено на высоте 20 м от ее основания прикрепить растяжки из стального каната, которые закрепить к четырем бетонным тумбам, находящимся на расстоянии 15 м от основания трубы. Сколько каната для этого потребуется? (Рис. 2.)
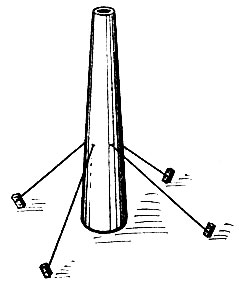
Рис. 2
Решение. Примем дымовую трубу за отрезок прямой, перпендикулярной поверхности земли, а бетонные тумбы – за точки на поверхности земли. Так как для нахождения длины всего потребного каната для четырех растяжек достаточно найти длину одной из них, то получаем такую геометрическую задачу: “Найти длину гипотенузы прямоугольного треугольника, катеты которого равны 20 и 15 метрам”.
В этом примере реальные объекты – труба, бетонные тумбы, канаты – мы заменили математическими объектами – отрезками прямых, точками, для чего пришлось абстрагироваться (отвлечься, не учитывать) от таких особенностей этих реальных объектов, как конусность и толщина трубы, размеры тумб, высота их над поверхностью земли и т. д. Иными словами, реальное явление, описанное в приведенной задаче, мы заменили идеализированным явлением – геометрической задачей, а поэтому наше решение является приближенным. Однако точность здесь вполне достаточная для практики (ошибка может быть в пределах нескольких сантиметров).
Вообще надо помнить, что математическое решение любой практической задачи всегда является приближенным.
Для того чтобы закрепить полученные знания и проверить себя, как вы их усвоили, выполните следующее задание.
Задание 2
2.1. Какие геометрические фигуры выступают в качестве идеальных образов (моделей) реальных предметов в следующих практических задачах:
а)Найти площадь пятикопеечной монеты.
б) Найти длину обруча.
в) Найти площадь комнаты.
От каких свойств реальных предметов мы при этом абстрагируемся, а какие учитываем?
2.2. За билетами в театр стоит очередь. Какие математические объекты характеризуют положение (место) каждого человека в этой очереди? Какие практические задачи можно решить с помощью этих математических объектов?
2.3. Велосипедист выехал из города А в 9 ч утра и прибыл в город В, отстоящий от А на расстоянии 60 км, в 12 ч дня. Отдохнув в В 2 ч, он поехал дальше в город С, отстоящий от В на 72 км, и прибыл туда в 6 ч вечера.
Как можно наиболее просто и наглядно математически описать событие поездки велосипедиста из А в С? Какие практические задачи можно решить, имея это математическое описание? Какие математические объекты при этом использованы?
Источник
Существенные и несущественные свойства
математических объектов раскрываются в процессе
определения понятий математики. Множество
существенных свойств составляют содержание
понятия.
Под существенными свойствами будем понимать
те, без которых понятие не существует, и при
помощи которых выделяются объекты интересующего
нас множества. Существенные свойства – это
всегда общие свойства, но обратное неверно –
общие свойства могут быть несущественными. Так, в
школьных учебниках в уравнениях преобладает
обозначение переменной – “х”. Это свойство
общее, но не существенное.
Кроме того, понятия “существенное” и
“несущественное” свойство относительны, в
разных ситуациях одно и то же свойство
математического объекта может быть как
существенным, так и несущественным. Например, при
выделении линейных функций среди других знак
коэффициента при х – несущественное
свойство, но оно же становится существенным при
выделении среди линейных функций возрастающих.
Существенные свойства понятия в определении
могут быть связаны между собой конъюнктивно,
дизъюнктивно и в сочетании конъюнкции и
дизъюнкции. Большинство школьных определений –
конъюнктивны. Если
– существенные свойства какого-либо
математического понятия Р, то:
• если математический объект не обладает хотя
бы одним из свойств , то этот объект не принадлежит понятию Р;
• если математический объект обладает всеми
существенными свойствами , то он обязательно принадлежит
понятию Р.
Понять эту непростую закономерность ребятам
помогает такое объяснение материала, при котором
после введения определения ученикам
предъявляются математические объекты со
свойствами ; . Учащиеся
должны мотивированно ответить на вопрос, почему
эти объекты не принадлежат понятию Р. Такая
работа позволяет за один урок сформировать в
сознании ребят математическое понятие.
Процесс выделения свойств математических
объектов, отделения существенных от
несущественных очень сложен. Чтобы помочь в этом,
можно применять на уроках задания следующих
четырех типов.
Первый из них – учащимся известно определение
математического понятия и они с помощью учителя
или самостоятельно формулируют основные
существенные свойства этого понятия, заем
проверяют, обладают ли предложенные им
математические объекты этими свойствами.
Примером могут служить следующие задания:
• Сформулируйте определение линейной функции.
Укажите, какая из следующих функций является
линейной, а какая – нет. Поясните, почему?
; ; ; ; ; ; ; ; ; .
• Сформулируйте известные вам свойства
понятия функции. Укажите, какая из ломаных,
изображенных на рисунке, является графиком
функции:
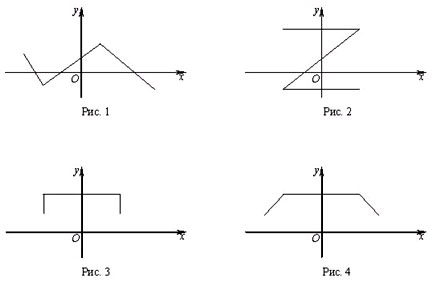
Поясните свой ответ.
Задания второго типа состоят в том, что
учащиеся должны назвать математический объект
по перечисленным его свойствам.
1. Функция … принимает наибольшее значение при .
2. Функция … возрастает на интервале и убывает на
интервале .
3. График функции … симметричен относительно
прямой .
4. График функции … расположен в III и IV
координатных четвертях.
5. График функции … проходит через точку .
6. Точка пересечения графика функции … с осью ОУ
– .
Какая квадратичная функция обладает этими
свойствами? Задайте ее аналитической формулой и
постройте график этой функции.
Задания третьего типа – это задания, в которых
нужно выделить существенные свойства
математических объектов и привести
самостоятельно примеры объектов, обладающих
такими же свойствами или отбросить лишние
объекты:
• Какое из числовых выражений вы назвали бы
лишним в этой таблице?
Поясните свой ответ.
• Запишите еще несколько членов числовой
последовательности, задайте ее общий член
формулой:
.
В заданиях четвертого типа от учащихся
требуется добавить свойство или свойства, чтобы
от одного математического объекта перейти к
другому. На уроках геометрии предлагается
задание:
• Укажите то условие, которое нужно добавить,
чтобы от одного четырехугольника перейти к
другому. Назовите все известные вам свойства
перечисленных геометрических фигур.
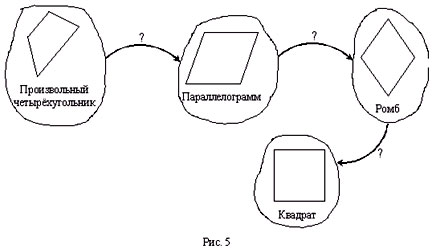
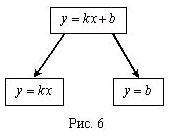
• Укажите условия, необходимые для того, чтобы
перейти от одной функции к другой. Назовите все
известные вам свойства указанных функций.
Прием расчленяющей абстракции (Е.Н.
Кобанова-Меллер) при изучении понятий выражается
в таких действиях:
а) выделяются существенные свойства
математических объектов, они остаются
инвариантными в процессе формирования понятия;
б) выделяются несущественные свойства тех же
объектов и принцип их вариаций, в процессе
формирования понятия используются вариации
несущественных свойств.
После знакомства с графиками функций,
содержащих модули, можно предложить учащимся
графически решить уравнение, содержащее модуль и
параметр.
• Найти все значения а, при которых
уравнение имеет
ровно два корня.
Данное уравнение имеет вид , где ; .
Раскрывая знаки модулей в , рассмотрим три случая:
1) : .
2) : .
3) : .
Запишем в
виде:
Решим данное уравнение графически, построив в
системе координат ОХУ графики функций и . Заметим, что задает множество прямых,
параллельных оси ОХ.
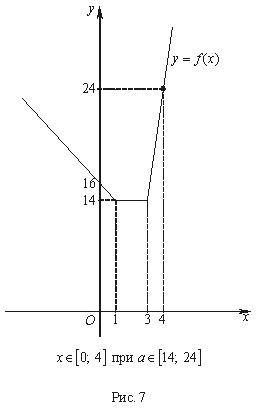
Решением задачи будет промежуток .
Учитель может варьировать задания:
• Найти все а, при которых уравнение
1) имеет ровно два корня;
2) имеет ровно три корня;
3) имеет бесконечно много корней;
4) не имеет корней;
5) имеет хотя бы одни корень;
6) имеет хотя бы один корень, причем все его
корни принадлежат отрезку .
Другое направление варьирования исходного
задания – изменять :
• Найти все а, при которых уравнение:
1)
2)
3)
имеет два корня.
Наконец, варьированию поддаются функции,
входящие в левую часть исходного уравнения:
• Найти все а, при которых уравнение:
1)
2)
3)
имеет ровно два корня.
Из получившихся заданий учитель может выбрать
материал для “Урока одной задачи”, учитывая
особенности своего класса.
Источник
Математика Основные свойства объектов
Количество просмотров публикации Основные свойства объектов – 1410
| Наименование параметра | Значение |
| Тема статьи: | Основные свойства объектов |
| Рубрика (тематическая категория) | Математика |
Объекты характеризуются определенными свойствами (линейностью, постоянством или переменностью параметров, инерционностью и т. п.), оказывающими большое влияние на выбор методов анализа или синтеза систем автоматического регулирования. Так, для линейных объектов целесообразно применять хорошо разработанные частотные методы анализа и синтеза систем. Стоит сказать, что для нелинейных объектов приходится использовать более громоздкие методы: фазовой плоскости или гармонической линеаризации.
Методы фазовой плоскости разработаны лишь для систем управления описываемых нелинейными дифференциальными уравнениями низких порядков (обычно второго и третьего). Методы гармонической линеаризации хотя и не имеют ограничений на порядок нелинейных дифференциальных уравнений, однако, являются приближенными. Для повышения их точности иногда приходится учитывать поправки на первую гармонику входного сигнала от высших гармоник. Следует отметить, что существуют такие объекты регулирования, к которым невозможно применять методы гармонической линеаризации.
Наличие линейности у объекта проверяется по его реакции на входные воздействия, одинаковые по величине и различные по знаку. В случае если при действии таких сигналов переходные характеристики по своей форме идентичны и различаются только знаками, то рассматриваемый объект является линейным. Это означает, что для него справедлив принцип суперпозиции, и математическое описание объекта можно выполнить с помощью линейных дифференциальных или разностных уравнений. В случае если объект реагирует по-разному на данные типы входных сигналов, то для него несправедлив принцип суперпозиции, и он должна быть математически описан нелинейными дифференциальными или разностными уравнениями.
Большое влияние на описание объектов регулирования оказывает принятая степень идеализации процессов, протекающих в объектах. В случае если динамика линейного объекта определяется конечным числом переменных, то его поведение описывается дифференциальными уравнениями с сосредоточенными постоянными (обыкновенными дифференциальными уравнениями). В случае если число переменных бесконечно велико, то поведение объекта описывается дифференциальными уравнениями с распределенными постоянными (дифференциальными уравнениями в частных производных).
При проектировании систем автоматического регулирования с объектами, имеющими распределенные параметры, уравнения динамики в частных производных довольно часто приводят к обыкновенным дифференциальным уравнениям (системам дифференциальных уравнений).
Во многих объектах регулирования параметры объекта регулирования не являются постоянными, а зависят от времени. К примеру, параметр летательного аппарата изменяются исходя из скорости его полета по закону V = V (t). В этом случае динамика летательного аппарата (самолета͵ ракеты) описывается дифференциальным уравнением с переменными параметрами. В случае если же у объекта регулирования изменение параметров от времени носит случайный характер, то динамика процессов в таком объекте описывается стохастическим дифференциальным уравнением. К таким объектам можно отнести усилители сигналов с автоматической регулировкой в радиолокационных станциях, выходные блоки в радиорелейных линиях и т. д.
В процессе проектирования автоматической системы определяют инерционность объекта регулирования. Для этого на его вход подают ступенчатое единичное воздействие, а с выхода снимают переходную характеристику. Чем медленнее происходит нарастание переходной характеристики, тем большей инерционностью обладает объект регулирования. Можно отметить, что регулирование объектов с повышенной инерционностью осуществляется достаточно сложно, так как при этом трудно удовлетворить требуемым показателям качества. Регулирование малоинерционных объектов также представляет значительные трудности из-за крайне важно сти применения быстродействующих исполнительных устройств. Наиболее просто обеспечивается регулирование объектов со средней инерционностью.
У некоторых объектов регулирования наряду со значительной инерционностью имеет место ʼʼчистоеʼʼ запаздывание выходного сигнала, что также ухудшает показатели качества процессов регулирования.
Объекты регулирования различают и по степени самовыравнивания. В случае если при действии на вход объекта регулирования ступенчатого единичного сигнала происходит асимптотический процесс нарастания выходного сигнала до установления определенного уровня, то принято считать, что такой объект регулирования обладает положительным самовыравниванием. В случае если _ при действии на вход объекта ступенчатого единичного сигнала сигнал на его выходе все время нарастает, то объект регулирования обладает отрицательным самовыравниванием. И, наконец, в случае если при действии ступенчатого единичного сигнала на объект на его выходе происходит линейное нарастание сигнала, то объект регулирования имеет нулевое самовыравнивание.
Основные свойства объектов – понятие и виды. Классификация и особенности категории “Основные свойства объектов” 2017, 2018.
Источник
