Какими свойствами характеризуется качество оценок параметров
| Для понимающего достаточно и немногого. Стендаль. “Пармская обитель”. |
Значение параметра, вычисленное по ограниченному объему ЭД, является случайной величиной, т. е. значение такой величины от выборки к выборке может меняться заранее не предвиденным образом. Следовательно, в результате обработки ЭД определяется не значение параметра T, а только лишь его приближенное значение – статистическая оценка параметра q. Получить статистическую оценку параметра теоретического распределения означает найти функцию от имеющихся результатов наблюдения, которая и даст приближенное значение искомого параметра. Различают два вида оценок – точечные и интервальные. Точечныминазывают такие оценки, которые характеризуются одним числом. При малых объемах выборки точечные оценки могут значительно отличаться от истинных значений параметров, поэтому их применяют при большом объеме выборки. Интервальныеоценки задаются двумя числами, определяющими вероятный диапазон возможного значения параметра. Эти оценки применяются для малых и для больших выборок. Рассмотрим вначале точечные оценки.
Применительно к каждому оцениваемому параметру закона распределения генеральной совокупности существует множество функций, позволяющих вычислить искомые значения. Например, оценку математического ожидания можно вычислить, взяв среднее арифметическое выборочных значений, половину суммы крайних членов вариационного ряда, средний член выборки и т.д. Указанные функции отличаются качеством оценок и трудоемкостью реализации.
Качество оценок характеризуется такими свойствами, как состоятельность, несмещенность, эффективность и достаточность [3, 5, 9].
Состоятельность характеризует сходимость по вероятности оценки q к истинному значению параметра T при неограниченном увеличении объема выборки n. Для состоятельности оценки достаточно, но не обязательно, чтобы математическое ожидание квадрата отклонения оценки от параметра M(T – q)2 стремилось к нулю с увеличением объема выборки (здесь и далее символ М означает математическое ожидание). Свойство состоятельности проявляется при неограниченном увеличении n, а при небольших объемах ЭД наличие этого свойства еще недостаточно для применения оценки.
Несмещенность характеризует отсутствие систематических (в среднем) отклонений оценки от параметра при любом конечном, в том числе и малом, объеме выборки, т. е. M(q) = T. Использование статистической оценки, математическое ожидание которой не равно оцениваемому параметру, приводит к систематическим ошибкам. Не всегда наличие смещения плохо. Оно может быть существенно меньше погрешности регистрации значений параметра или давать дополнительную гарантию выполнения требований к значению параметра (если даже при положительном смещении оценка q меньше предельно допустимого значения, то несмещенное значение тем более будет отвечать этому условию). В таких ситуациях допустимо применение смещенных оценок, если они вычисляются проще, чем несмещенные. Но даже несмещенная оценка может быть удалена от истинного значения.
Эффективностьхарактеризует разброс случайных значений оценки около истинного значения параметра. Среди всех оценок следует выбрать ту, значения которой теснее сконцентрированы около оцениваемого параметра. Для многих применяемых способов оценивания выборочные распределения параметров асимптотически нормальны, поэтому часто мерой эффективности служит дисперсия оценки. В таком понимании эффективная оценка – это оценка с минимальной дисперсией. При неограниченном увеличении n эффективная оценка является и состоятельной. В случае оценивания одного параметра дисперсия несмещенной оценки отвечает условию Рао – Крамера,
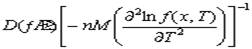
где f(x, T) – плотность распределения варианты; п – количество наблюдений.
Сравнительная эффективность оценки с дисперсией Dk(q) измеряется коэффициентом эффективности
e = D(q)/Dk(q),
который не превышает единицы. Чем ближе коэффициент e к единице, тем эффективнее оценка. Отмеченное ограничение применимо и к дискретным распределениям, если вместо плотности распределения подставить в него функцию вероятности.
Достаточностьхарактеризует полноту использования информации, содержащейся в выборке. Другими словами, оценка q будет достаточной, если все другие независимые оценки на основе данной выборки не дают дополнительной информации об оцениваемом параметре. Эффективная оценка обязательно является и достаточной.
Рассмотренные свойства применимы также и к ЭД, которые характеризуются многомерными распределениями вероятностей.
Подходы к формированию оценок разработаны в теории несмещенных оценок , предложенной А. Н. Колмогоровым и С. Рао. В данной теории предполагается известным с точностью до параметра T вид функции плотности распределения наблюдаемой величины f(x, Т). Вид распределения устанавливается исходя из априорных соображений, например, на основе общепринятых суждений о характере безотказной работы технических средств. Тогда задача сводится к нахождению такой функции от результатов наблюдений, которая дает несмещенную и эффективную оценку.
Источник
При исследовании различных параметров генеральной совокупности на основе выборки возможно лишь получение оценок этих параметров. Необходимые оценки строятся на основе ограниченного набора данных, что влечет за собой определенную вероятность погрешности в статистических выводах. Заметим, что значения оценок могут изменяться от выборки к выборке.
Процесс нахождения оценок неизвестного генерального параметра θ, от которого зависит распределение СВ Х, будем называть оцениванием. Цель любого оценивания – получение наиболее точного значения оцениваемой характеристики (наилучшей оценки). Обычно на начальном этапе эконометрических исследований берутся выборочные числовые характеристики, рассмотренные в предыдущем параграфе. Затем, исследуя соответствующую оценку, ее уточняют таким образом, чтобы она удовлетворяла основным целям оценивания. Различают два вида оценок параметров распределения генеральной совокупности – точечные и интервальные.
Точечной оценкой параметра θ называется числовое значение этого параметра, полученное по определенным правилам по выборке объема n. Например, оценками параметров нормального распределения m и σ(Х) могут быть и σв. Оценка является функцией выборки, отобранной для изучения, и может рассматриваться как СВ со своими числовыми характеристиками. «Наилучшая оценка» должна обладать наименьшим рассеиванием относительно оцениваемого параметра θ, т. е. должна иметь наименьшую дисперсию среди всех других оценок. Число ε такое, что называется точностью (абсолютной погрешностью) оценки.
Рассмотрим свойства, выполнимость которых желательна для того, чтобы оценка была признана удовлетворительной. Качество оценок будем характеризовать следующими основными параметрами: несмещенность, эффективность и состоятельность.
Оценка параметра θ называется несмещенной, если ее математическое ожидание равно оцениваемому параметру: М( ) = θ. Если это равенство не выполняется, то оценка является смещенной и разность М( ) – θ будет называться смещением или систематической ошибкой оценивания. Соответственно, оценка будет в среднем занижать (если М( ) – θ < 0), либо завышать (если М( ) – θ > 0) значение параметра θ.
Несмещенная оценка называется эффективной оценкой параметра θ, если она имеет наименьшую дисперсию среди всех возможных несмещенных оценок при фиксированном объеме выборки n.
Оценка называется асимптотически эффективной, если с увеличением объема выборки ее дисперсия стремится к нулю (Dn( ) ® 0, при n ® ¥).
Оценка параметра θ называется состоятельной, если она сходится по вероятности к оцениваемому параметру:
, (1.38)
для любого сколь угодно малого ε > 0.
Другими словами, состоятельной является такая оценка, которая, согласно закону больших чисел, дает истинное значение параметра при достаточно большом объеме выборки.
Оценки, являющиеся линейными функциями от выборочных наблюдений, называются линейными. Важную роль в эконометрике играют наилучшие линейные несмещенные оценки, которые имеют наименьшую дисперсию среди всех возможных оценок данного класса.
Наиболее известными методами нахождения точечных оценок параметров генеральной совокупности являются метод моментов, метод максимального правдоподобия, метод наименьших квадратов. Здесь мы кратко остановимся на описании метода максимального правдоподобия [16], поскольку метод наименьших квадратов будет рассмотрен в последующих главах как основной метод нахождения оценок параметров регрессионных эконометрических моделей.
Пусть СВ Х представлена выборкой x1, x2, …, xn и имеет плотность распределения f(x, θ), зависящую от неизвестного параметра θ. Согласно методу максимального правдоподобия, в качестве оценки параметра θ принимается такое значение , которое максимизирует функцию правдоподобия L:
, (1.39)
выражающую плотность вероятностей совместного появления результатов выборки x1, x2, …, xn. В большинстве случаев более эффективно рассматривать логарифмическую функцию правдоподобия l = lnL. Необходимым условием максимума является уравнение ( ), которое называется уравнением правдоподобия. Для широкого класса задач оценки метода максимального правдоподобия являются состоятельными и асимптотически эффективными. В то же время они могут быть смещенными. Недостатком метода является необходимость знать закон распределения СВ.
Например, с помощью несложных преобразований можно показать, что оценками максимального правдоподобия для нормальной генеральной совокупности являются выборочное среднее и выборочная дисперсия . Выборочное среднее является несмещенной и состоятельной оценкой математического ожидания М(Х) генеральной совокупности. Выборочная дисперсия является смещенной оценкой дисперсии генеральной совокупности D(X) = σ2, так как доказано, что Dв = σ2 · (n – 1)/n. Иными словами, выборочная дисперсия оценивает генеральную дисперсию D(X) с недостатком. Несмещенной и состоятельной оценкой будет исправленная выборочная дисперсия
. (1.40)
Следует заметить, что при n ® ¥ и оценка Dв является асимптотически несмещенной. Различие между Dв и S2 при n > 30 практически отсутствует. Поэтому при достаточно большом объеме выборки обе дисперсии можно считать несмещенными оценками.
В соответствии с S2 вводится исправленное среднее квадратическое отклонение (эмпирический стандарт) S:
. (1.41)
Относительная частота является несмещенной и состоятельной оценкой вероятности Р(Х = хi). Соответственно, эмпирическая функция распределения (накопленная относительная частота) является несмещенной и состоятельной оценкой теоретической функции распределения F(x) = P(X < x).
Наряду с точечными оценками параметров рассматривают интервальные оценки, которые позволяют получить информацию о точности и надежности оценивания неизвестного параметра, что особенно важно для выборок небольшого объема.
Интервальной оценкой параметра θ называют числовой интервал , который с заданной вероятностью γ накрывает неизвестное точное значение оцениваемого параметра. При этом указанный интервал называют доверительным интервалом, а вероятность γ – доверительной вероятностью или надежностью оценки.
Величина доверительного интервала, характеризующая точность оценки, зависит от объема выборки n (уменьшается с ростом n) и надежности γ (увеличивается с приближением γ к единице). Зачастую для определения доверительного интервала заранее выбирают число α = 1 – γ, называемое уровнем значимости, и находят два числа и , такие, что
. (1.42)
В этом случае говорят, что доверительный интервал накрывает неизвестный параметр θ с вероятностью 1 – α или в 100(1 – α)% случаев. Границы интервала обычно находятся из условия Р(θ < ) = P(θ > ) = α/2. Выбор γ (или α) определяется необходимой надежностью оценки. Обычно используется α = 0,1; 0,05; 0,01, что соответствует 90, 95 и 99%-м доверительным интервалам.
Поскольку в эконометрических задачах часто приходится находить доверительные интервалы параметров СВ, приведем примеры их построения.
Доверительный интервал для математического ожидания нормальной СВ. Из генеральной совокупности нормально распределенной СВ Х с параметрами m и σ извлекается выборка объема n. В качестве точечной оценки математического ожидания m используется выборочное среднее .
В силу свойств многомерного нормального распределения [2] величина (статистика) , где – исправленное выборочное среднее квадратическое отклонение, имеет распределение Стьюдента с n – 1 степенями свободы. Тогда, при требуемом уровне значимости α, доверительный интервал для математического ожидания, накрывающий неизвестное значение m с надежностью 1 – α, определятся из следующих соотношений:
(1.43)
. (1.44)
Доверительный интервал для дисперсии нормальной СВ. Для оценки σ2 извлекается выборка объема n. В качестве точечной оценки дисперсии σ2 = D(X) используется исправленная выборочная дисперсия S2. Учитывая, что статистика имеет χ2-распределение с n – 1 степенями свободы, доверительный интервал для неизвестного значения генеральной дисперсии σ2 на уровне значимости α определяется по формуле:
. (1.45)
Для заданного α критические точки определяются по соответствующим таблицам (Приложения 2-6).
Источник
Эконометрика занимается в основном оценкой параметров экономических зависимостей и проверкой гипотез, относящихся к этим параметрам. Например, вновь рассмотрим простейшую кейнсианскую функцию потребления, связывающую потребление с доходом:
(1.13)
В экономической теории предлагается линейная форма функции потребления и даже обосновывается наличие ограничений на параметры. Например, если интерпретировать как автономное потребление, а — как предельную склонность к потреблению, то разумно считать, что
Однако экономическая теория обычно не отвечает на вопрос о точных значениях параметров модели. Даже если точное значение параметра теоретически обосновано, эконометрист все равно может интересоваться оценкой параметра с целью проверки соответствия эмпирических данных и теоретических результатов. Таким образом, Назначение эконометрики состоит в том, чтобы получать оценки неизвестных параметров в эмпирических экономических моделях и проверять связанные с ними гипотезы.
Например, используя ежегодные данные за период 1929- 1940 гг. о совокупном потреблении и доходе в США и учитывая инфляцию и рост населения, можно получить следующую оценку уравнения (1.13):
(1.14)
Таким образом, оценки автономного потребления и предельной склонности к потреблению составили, соответственно 11,45 и 0,78. Эти числа получены по определенным эконометрическим формулам. По традиции, сложившейся в русскоязычной литературе, как сами эти формулы, так и результаты вычислений по ним, называются оценками. В то же время в английской терминологии используются два разных понятия: estimator — оценка, «оценщик», т. е. формула для оценивания, и estimate — оценка, оцененное значение, т. е. результат оценивания.
Вообще говоря, для оценивания одних и тех же параметров эконометрической модели могут быть предложены различные формулы (методы), которые, очевидно, будут приводить к разным результатам. Одни из них могут быть явно хуже других, но в некоторых случаях предпочтительность одних оценок перед другими не так очевидна. Таким образом, необходимо иметь набор формальных критериев, по которым можно было бы «проверить качество» методов оценивания.
1.4.1. Распределение оценки Рассмотрим модель:
(1.15)
где , — белый шум.
Уравнение (1.15) задает предполагаемый процесс генерации значений . Выберем какой-нибудь метод оценивания параметра и обозначим соответствующую формулу для оценки через . По конкретным наблюдённым значениям временных рядов у и х можно получить конкретное значение оценки. Однако данные временные ряды — это одна из возможных реализаций случайных процессов, поэтому, рассуждая теоретически, мы могли бы вместо данной реализации иметь несколько другую реализацию и (на основе той же самой формулы ) Получить другой числовой результат. Теоретически значение оценки будет меняться в зависимости от различных реализаций. Это служит основанием для того, чтобы считать, что оценка является случайной величиной, имеющей неконтролируемый разброс, обусловленный случайностью механизма формирования наблюдаемого временного ряда. Так мы приходим к понятию Распределения Оценки, которое задается законом распределения вероятностей случайной величины и позволяет вычислить вероятность попадания оценки в любой указанный интервал.
Для конкретности предположим, что х является по сути детерминированной (неслучайной) переменной с заранее заданными фиксированными значениями: например, х может быть временным параметром со значениями 1, 2, 3, …, П. Тогда, воспользовавшись генератором случайных чисел, мы могли бы произвести серию, например, из 2500 экспериментов Монте — Карло, Генерируя в каждом из них реализацию ряда случайных ошибок
, длиной П. Имея фиксированный временной ряд для Х И используя уравнение (1.15), в котором значение зафиксировано, например, на уровне =З,5, можно рассчитать 2500 временных рядов для У. Поскольку в ходе проведения эксперимента истинное значение известно, то, построив 2500 реализаций оценки по Повторным выборкам, Можно определить характер распределения значений оценки по отношению к . Для этого строится гистограмма значений оценки, которая является эмпирической аппроксимацией ее теоретического закона распределения. Метод Монте-Карло используется для построения Эмпирического распределения Оценки в том случае, когда модель или метод оценивания особенно сложны и поведение оценки не под- дается теоретическому анализу. Однако часто свойства распределения оценки можно вывести, считая, что для модели выполняются те или иные предположения.
Качество оценки (метода оценивания) обычно проверяется путем анализа свойств ее распределения. В частности, метод оценивания будет очевидно предпочтительнее, если вероятность того, что он даст оценку, близкую к истинному (но неизвестному) значению оцениваемого параметра, будет достаточно велика.
1.4.2. Несмещенность
Первое из рассматриваемых свойств — несмещенность. Оценка параметра называется Несмещенной, Если ее математическое ожидание равно истинному значению оцениваемого параметра. Это означает, что положительные и отрицательные отклонения значений оценки, полученные (по разным выборкам), взаимно компенсируются», т. е. осреднение (по все возможным выборкам) значений оценки дает истинное значение параметров.
Разумеется, не всякая оценка является несмещенной. Назовем Смещением оценки Разность между ее математическим ожиданием и истинным значением оцениваемого параметра:
(1.16)
При В 0 оценка является Смещенной. Ясно, что при наличии достаточно большого смещения и относительно малого разброса (дисперсии) оценки вокруг своего математического ожидания значения оценки не будут концентрироваться рядом с истинным значением параметра. Таким образом, использование несмещенных оценок часто оказывается более предпочтительным.
Рассмотрим теперь две оценки одного и того же параметра, распределения которых обладают следующими свойствами: — несмещенная оценка с большой дисперсией; — оценка с небольшим смещением, но сравнительно малой дисперсией. В данном случае более предпочтительной будет оценка , поскольку ее значения, вычисленные по различным выборкам (теоретически возможным при повторениях наблюдений), будут чаще оказываться в окрестности истинного значения параметра . Данный пример подчеркивает важную роль дисперсии оценки как измерителя качества оценивания.
1.4.3. Наилучшая несмещенная оценка
Как было показано выше, решение О Том, какой метод оценивания «лучше», должно основываться на рассмотрении не только математических ожиданий оценок, но и их дисперсий. Однако говорить об оценке с «минимально возможной> дисперсией следует с осторожностью.
Предположим, например, что для оценки параметра в модели (1.15) Используется оценка =123,4 , принимающая одно и то же значение вне зависимости от содержательного смысла задачи или имеющихся выборочных данных. Поскольку эта оценка не меняется, ее дисперсия равна нулю наименьшему из возможных значений. По этой причине, очевидно, необходимо ограничить поиск минимальной дисперсии каким-либо классом оценок. Обычно это достигается за счет рассмотрения только несмещенных оценок.
Рассмотрим две несмещенные оценки, одна из которых () Имеет распределение с меньшей дисперсией, чем другая оценка (). Ясно, что более приемлем метод оценивания по формуле , так как она чаще будет давать оценку, близкую к истинному значению оцениваемого параметра, чем .
Оценка, которая имеет наименьшую дисперсию среди оценок некоторого класса, называется Наиболее эффективной Или Наилучшей В этом классе.
Вообще говоря, существует общий подход к выбору оценок — Принцип максимального правдоподобия, Использование которого во многих ситуациях позволяет получать наилучшую несмещенную оценку, если она существует. Однако часто бывает удобно ограничиться рассмотрением оценок, являющихся линейными функциями ошибок. Оценка, которая является Линейной, Несмещенной и имеет наименьшую дисперсию среди всех линейных несмещенных оценок, называется Наилучшей линейной несмещенной оценкой.
Если мы оцениваем более чем один параметр, то понятие эффективности необходимо уточнить. При наличии двух оценок и K-мерного векторного параметра обычно сравнивают ковариационные матрицы этих оценок, имеющие размерности K K. Если разность ковариационных матриц Var() — Var() неотрицательно
определена, то говорят, что векторная оценка является более эффективной, чем .
1.4.4. Асиiiптотические свойства оценок
Следует подчеркнуть, что рассмотренные выше теоретические свойства «хорошей» оценки (несмещенность, эффективность) должны выполняться при любом фиксированном объеме выборочных наблюдений, используемых при ее вычислении. Так, например, математическое ожидание несмещенной оценки должно совпадать с оцениваемым параметром вне зависимости от количества имеющихся наблюдений. Однако во многих случаях оценка с такими свойствами не существует. Тогда следует обратиться К асимптотическим Свойствам оценки, т. е. посмотреть, как она ведет себя, когда используется очень большое (неограниченно растущее) количество выборочных наблюдений. Иногда, если известны только асимптотические свойства рассматриваемой оценки, ее поведение при малых объемах выборки исследуют путем имитации подходящего механизма получения данных с помощью метода Монте-Карло.
Интуитивное представление о том, чем занимается асимптотическая теория, можно получить с помощью все тех же экспериментов Монте-Карло. Пусть данные формируются в соответствии с уравнением (1.15) При заданном значении параметра , причем объясняющая переменная х имеет неслучайный характер (например, является временем) и, таким образом, список ее значений заранее известен и фиксирован. При заданном объеме выборки Т Первый шаг процедуры Монте-Карло состоит в генерации последовательности значений случайных ошибок , t = ( 1, 2, …, Т И соответствующих значений зависимой переменной . На втором шаге по полученным данным и известной формуле оценочной функции вычисляется значение оценки параметра . Многократное повторение этой двух шаговой процедуры (при одном и том же объеме выборки Т) позволит получить достаточно длинную серию реализаций оценки и построить по ней гистограмму распределения этой оценки.
Изложенная процедура многократной генерации временных рядов и у определенной длины Т с последующим вычислением гистограммы распределения оценки может быть реализована для некоторого начального значения Т = Т0, например, для 100 наблюдений. Далее такие же эксперименты Монте-Карло можно повторить для Т = Т0 + 1, затем для Т = Т0 + 2 и так далее, увеличивая Т. При каждом значении Т будет получено отдельное эмпирическое распределение, соответствующее оценке . Если свойства оценки не зависят от объема выборки Т, то гистограммы распределений будут выглядеть практически одинаково. Если же объем выборки сказывается на поведении оценки, то вид распределений (их форма и/или положение) будет меняться при росте Т.
Осуществление подобных компьютерных экспериментов необходимо далеко не всегда. Во многих случаях поведение оценок при больших Т можно исследовать математически. Свойства оценок, полученные при , называются асимптотическими свойствами.
Как мы упоминали ранее, форма и положение эмпирического распределения для малых значений Т может рассматриваться для того, чтобы проверить свойства оценки при малом объеме выборки, если они не могут быть получены математически. Заметим, что последовательность , T=T0, Т0 + 1, Т0 + 2 …, где обозначает оценку (формулу для оценивания), вычисляемую по выборке объема Т, сама является случайным процессом, так как каждый член этой последовательности — случайная величина, принимающая те или иные значения в зависимости от конкретной реализации наблюдаемых временных рядов.
Предел распределения оценки, если он существует, при стремлении Т к бесконечности, называется асимптотическим распре делением оценки. Если математическое ожидание оценки стремится к истинному значению оцениваемого параметра, то оценка называется асимптотически несмещенной. Однако чаще нас будет интересовать другое асимптотическое свойство — состоятельность. Образно говоря, оценка называется состоятельной, если по мере увеличения числа наблюдений Т Значения (распределение значений) оценки все сильнее концентрируются вокруг истинного значения параметра. Формально Состоятельность Означает, что вероятность того, что разность между значением оценки и истинным значением параметра превзойдет произвольно заданную (сколь угодно малую) величину, должна стремиться к нулю при стремлении объема выборки к бесконечности:
(1.17)
Если оценка состоятельна, т. е. для нее выполняется предельное соотношение (1.17), То говорят, что ее Предел по вероятности Равен истинному значению оцениваемого параметра, и пишут
(1.18)
Таким образом, «состоятельность» и «сходимость по вероятности» — это синонимы.
Если оценивается вектор параметров, то оценка считается состоятельной, если каждая компонента вектора оценок сходится по вероятности к соответствующей компоненте вектора истинных значений параметров.
Пусть имеется две оценки, вычисляемые по выборке объема Т, и такие, что наряду с соотношением (1.18) Выполняется также
(1.19)
Тогда справедливы следующие свойства пределов по вероятности:

Если — константа, то
(1.20,е)
Если — непрерывная функция, то
(1.20,F)
Утверждение (1.20,F) называется теоремой Слуцкого. Оно справедливо не только в случае одного числового параметра , но и если — вектор. Тогда — непрерывная функция соответствующего числа аргументов. Легко заметить, что свойства (1.20, а), (1.20, b), (1.20, c) и (1.20, d) являются следствиями теоремы Слуцкого.
Следует обратить внимание на различия между понятиями математического ожидания и дисперсии асимптотического распределения оценки при Т , пределами математического ожидания и дисперсии оценки при Т и пределом по вероятности оценки при Т.
В некоторых случаях пределы математического ожидания и дисперсии оценки при Т могут не существовать, в то время как математическое ожидание и дисперсия асимптотического распределения существуют, поэтому использование моментов асимптотического распределения считается более удобным.
Достаточное условие состоятельности оценки состоит в том, чтобы среднее асимптотического распределения было равно истинному значению параметра и дисперсия асимптотического распределения равнялась нулю. Приведем пример, показывающий, что это условие не является необходимым.
Предположим, что распределение оценки при фиксированном объеме выборки Т с вероятностью, практически равной единице, концентрируется в малой окрестности точки , а с оставшейся (почти нулевой) вероятностью может принимать значения близкие к Т. Точнее, пусть
и
Для простоты дальнейших выкладок будем дополнительно считать, что оценка имеет функцию плотности, которая принимает значение Т — 1 на отрезке длины 1/Т с центром в. т. очке , значение 1 на отрезке длины 1/Т с центром в точке Т и значение 0 в остальных случаях. Ясно, что такая оценка является состоятельной, так как
при . в результате прямых вычислений нетрудно получить следующие результаты:
и
Таким образом, предел математического ожидания оценки не совпадает с истинным значением оцениваемого параметра (асимптотической несмещенность нет) и, более того, асимптотически дисперсия оценки бесконечно велика, тем не менее оценка является состоятельной.
Источник
