Какими свойствами должны обладать оценки

Статистику иногда определяют как науку принятия разумных решений в условиях неопределенности, когда действуют те или иные случайные факторы. Во многих случаях экспериментатор принимает решения, руководствуясь здравым смыслом и статистическими выводами, извлеченными из опытных данных. Получение обобщающих выводов из данных – основная цель статистики.

В оставшейся части настоящей работы мы уделим внимание двум категориям статистических задач: оценивание (точечное и ин­тервальное) и проверка статистических гипотез. Это настолько об­ширные, глобальные темы, что мы познакомимся с ними лишь частич­но, делая ударение на методологии и примерах.

Например, у нас может возникнуть желание по наблюдениям, ко­торые предполагаются нормально распределенными, получить число – точечную оценку параметра σ2 , или же получить некоторый интервал, который с той или иной степенью достоверности содержит истинное значение параметра σ2 . Возможно, мы захотим проверить наше пред­положение о нормальности распределения, обращаясь к теории провер­ки статистических гипотез.

Точечные оценки.

Нередко, сделав допущение о типе закона распределения, ищут по выборке приближенные значения (точечные оценки) его параметров. Неизвестный параметр распределения обозначают , а его точечную оценку .

Итак, – истинное значение параметра, постоянное неизвестное число. В наших примерах под мы часто понимаем математическое ожидание МХ либо дисперсию DХ=σ2 cл. величины X. – число, полученное по выборке и близкое к . По разным выборкам оценка примет разные значения вблизи .

Величина случайная, а – нет.

Оценка вычисляется по выборке (X1 ,Х2 , . . . ,Хn ) , т.е. это функция выборки: =g (Х1 ,Х2 , . . . ,Хn ) , поэтому называется статистикой. Как же подобрать функцию g, т.е. какие операции надо производить с точками выборки, чтобы получить хорошую оценку? Но что значит “хорошую”? Будет ли для истинного среднего =МХ хорошей оценкой выборочное среднее ? А, может, лучше полусумма (Х(1)+X(n))/2 наибольшего и наименьшего наблюдения, или, например, выборочная медиана ?

По сути дела под хорошей мы понимаем такую оценку, которая с большой вероятностью близка к истинному . Уточняя сказанное, рассмотрим три желательных свойства точечной оценки .

1. Состоятельность. Оценка состоятельна, если при увеличении объема выборки она неограниченно приближается к истинному . Для конечной генеральной совокупности оценка, полученная по всем элементам генеральной совокупности, даст точное значение . Когда же генеральная совокупность мыслится неограниченной, то состоятельность оценки означает, что при числе наблюдений n-> математическое ожидание оценки стремится к , а дисперсия ее к нулю:

(9)

Свойство состоятельности говорит, какова оценка при , и ничего не говорит о том, какова она при реальных значениях n . По­этому состоятельность – необходимое требование к хорошей оценке, но недостаточное.

Как мы убедились, выводя формулу (8), МХn =МХ при любом n, а DХ=б2/n -> 0 при . Значит, выборочное среднее есть состоятельная оценка для математического ожидания МХ (здесь Хn= , а МХ = ). Но состоятельными будут также и такие оценки МХ : , , поскольку число 100 становится пренебрежимо мало по сравнению с .

2. Несмещенность. Это свойство связано с поведением оценки при каждом конкретном n. У оценки , как случайной величины, есть математическое ожидание M . Разность -М называют смещением оценки . Смещение – средняя ошибка оценки и, если, она равна нулю, то оценку называют несмещенной. Итак, оценку называют несмещенной, если для любого n

(10)

Несмещенность оценки обозначает, что при всяком n среднее значение оценки, взятое по всевозможным выборкам данного объема n, в точности равно истинному значению параметра.

Оценка для среднего МХ несмещенная:

М =МХ, а оценки и , упомянутые выше, смещенные, например

М =

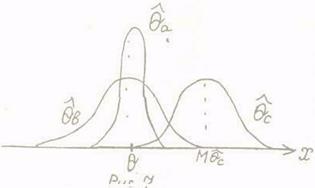
Пример 14. На рисунке 7 показаны для данного n законы распределения (плотности) трех оценок и параметра . Какая из оценок лучше?

Оценка лучше, чем , так как при одинаковой дисперсии оценка несмещенная: центр ее распределения совпадает с истинным . Величина М( – )=M – – смещение оценки , не равное нулю. Оценка не только несмещенная, но из трех оценок имеет меньшую дисперсию, значит, – лучшая из трех оценок.

3. Эффективность. Пусть для параметра мы имеем две несмещенные оценки (подобно и на рис.7) и выборку объема n. Какой оценкой пользоваться? Эффективна та, у какой меньше дисперсия.

Определение. Эффективной называется та из несмещенных оценок, у которой при данном объеме n минимальна дисперсия. Оказывается, наилучшей (точнее, эффективной) оценкой математического ожидания МХ нормальной величины является выборочное среднее . Мате­матическая статистика показывает, как строить эффективные или близкие к ним оценки параметров разных распределений. Легко показать, что оценка дисперсии S2 = (1/n)Σ(х1- )2 – выборочная дисперсия – является смещенной оценкой. Какому бы закону ни подчинялась cл.величина X, порождающая выборку, всегда среднее значение МS2 = DХ * (n-1)/n DХ. Чтобы получить несмещенную оценку , достаточно ввести небольшую поправку: = [n/(n-1)]* S2.

Для исправленной дисперсии имеем среднее:

Хотя при большом числе n состоятельные оценки S2 и практически совпадают при небольшом числе n лучше пользоваться несмещенной оценкой .

Сценка стандартного отклонения имеет несущественное для приложений смещение (это не противоречит несмещенности ).

Ранее мы ввели понятие моментов cл. величин и их оценок по выборке: статистических моментов. Как следствие закона больших чисел, статистические моменты являются состоятельными оценками теоретических моментов. Хотя эти оценки могут быть смещенными (например, оценка S2 дисперсии DХ), они по своим статистическим свойствам ненамного уступают эффективным оценкам, но выигрывают в простоте вычисления. Поэтому один из методов получения состоятельных оценок параметров распределения основан на моментах и так и называется “метод моментов”.

МЕТОД МОМЕНТОВ

Если параметр распределения сам является моментом, как МХ или DХ, то за его оценку в этом методе берут соответствующий статистический момент (например, или ). Когда интересует характеристика θ распределения, отличная от начального или центрального момента, ее выражают как функцию одного или нескольких моментов и затем в качестве аргументов этой функции вместо теоретических моментов подставляют статистические.

Например, если , то .

Пример. Найти формулу для оценки методом моментов срединного отклонения Е нормального распределения. Срединное отклонение , поскольку для нормальной величины X ~ N(μ,б2) вероятность Р{μ – 0, 674б<Х<μ+0, 6746 } = 1/2 .

Заменяя дисперсию в формуле на S2 – статистический центральный момент второго порядка, получим оценку срединного отклонения:

.

Пример.

Пусть неизвестный параметр – математическое ожидание. Тогда в нормальном распределении

Эта характеристика является состоятельной (закон больших чисел).

Пример.

Смещенная выборочная характеристика.

Пусть в нормальном распределении следует оценить дисперсию. Положим в качестве выборочной характеристики случайную величину

=

=

= ,

т.к.

Доказать, что выборочная характеристика

=

является несмещенной для дисперсии

=

Эконометрика занимается в основном оценкой параметров экономических зависимостей и проверкой гипотез, относящихся к этим параметрам. Например, вновь рассмотрим простейшую кейнсианскую функцию потребления, связывающую потребление с доходом:

(1.13)

В экономической теории предлагается линейная форма функции потребления и даже обосновывается наличие ограничений на параметры. Например, если интерпретировать как автономное потребление, а — как предельную склонность к потреблению, то разумно считать, что

Однако экономическая теория обычно не отвечает на вопрос о точных значениях параметров модели. Даже если точное значение параметра теоретически обосновано, эконометрист все равно может интересоваться оценкой параметра с целью проверки соответствия эмпирических данных и теоретических результатов. Таким образом, Назначение эконометрики состоит в том, чтобы получать оценки неизвестных параметров в эмпирических экономических моделях и проверять связанные с ними гипотезы.

Например, используя ежегодные данные за период 1929- 1940 гг. о совокупном потреблении и доходе в США и учитывая инфляцию и рост населения, можно получить следующую оценку уравнения (1.13):

(1.14)

Таким образом, оценки автономного потребления и предельной склонности к потреблению составили, соответственно 11,45 и 0,78. Эти числа получены по определенным эконометрическим формулам. По традиции, сложившейся в русскоязычной литературе, как сами эти формулы, так и результаты вычислений по ним, называются оценками. В то же время в английской терминологии используются два разных понятия: estimator — оценка, «оценщик», т. е. формула для оценивания, и estimate — оценка, оцененное значение, т. е. результат оценивания.

Вообще говоря, для оценивания одних и тех же параметров эконометрической модели могут быть предложены различные формулы (методы), которые, очевидно, будут приводить к разным результатам. Одни из них могут быть явно хуже других, но в некоторых случаях предпочтительность одних оценок перед другими не так очевидна. Таким образом, необходимо иметь набор формальных критериев, по которым можно было бы «проверить качество» методов оценивания.
1.4.1. Распределение оценки Рассмотрим модель:

(1.15)

где , — белый шум.
Уравнение (1.15) задает предполагаемый процесс генерации значений . Выберем какой-нибудь метод оценивания параметра и обозначим соответствующую формулу для оценки через . По конкретным наблюдённым значениям временных рядов у и х можно получить конкретное значение оценки. Однако данные временные ряды — это одна из возможных реализаций случайных процессов, поэтому, рассуждая теоретически, мы могли бы вместо данной реализации иметь несколько другую реализацию и (на основе той же самой формулы ) Получить другой числовой результат. Теоретически значение оценки будет меняться в зависимости от различных реализаций. Это служит основанием для того, чтобы считать, что оценка является случайной величиной, имеющей неконтролируемый разброс, обусловленный случайностью механизма формирования наблюдаемого временного ряда. Так мы приходим к понятию Распределения Оценки, которое задается законом распределения вероятностей случайной величины и позволяет вычислить вероятность попадания оценки в любой указанный интервал.
Для конкретности предположим, что х является по сути детерминированной (неслучайной) переменной с заранее заданными фиксированными значениями: например, х может быть временным параметром со значениями 1, 2, 3, …, П. Тогда, воспользовавшись генератором случайных чисел, мы могли бы произвести серию, например, из 2500 экспериментов Монте — Карло, Генерируя в каждом из них реализацию ряда случайных ошибок
, длиной П. Имея фиксированный временной ряд для Х И используя уравнение (1.15), в котором значение зафиксировано, например, на уровне =З,5, можно рассчитать 2500 временных рядов для У. Поскольку в ходе проведения эксперимента истинное значение известно, то, построив 2500 реализаций оценки по Повторным выборкам, Можно определить характер распределения значений оценки по отношению к . Для этого строится гистограмма значений оценки, которая является эмпирической аппроксимацией ее теоретического закона распределения. Метод Монте-Карло используется для построения Эмпирического распределения Оценки в том случае, когда модель или метод оценивания особенно сложны и поведение оценки не под- дается теоретическому анализу. Однако часто свойства распределения оценки можно вывести, считая, что для модели выполняются те или иные предположения.
Качество оценки (метода оценивания) обычно проверяется путем анализа свойств ее распределения. В частности, метод оценивания будет очевидно предпочтительнее, если вероятность того, что он даст оценку, близкую к истинному (но неизвестному) значению оцениваемого параметра, будет достаточно велика.

1.4.2. Несмещенность

Первое из рассматриваемых свойств — несмещенность. Оценка параметра называется Несмещенной, Если ее математическое ожидание равно истинному значению оцениваемого параметра. Это означает, что положительные и отрицательные отклонения значений оценки, полученные (по разным выборкам), взаимно компенсируются», т. е. осреднение (по все возможным выборкам) значений оценки дает истинное значение параметров.
Разумеется, не всякая оценка является несмещенной. Назовем Смещением оценки Разность между ее математическим ожиданием и истинным значением оцениваемого параметра:

(1.16)

При В 0 оценка является Смещенной. Ясно, что при наличии достаточно большого смещения и относительно малого разброса (дисперсии) оценки вокруг своего математического ожидания значения оценки не будут концентрироваться рядом с истинным значением параметра. Таким образом, использование несмещенных оценок часто оказывается более предпочтительным.

Рассмотрим теперь две оценки одного и того же параметра, распределения которых обладают следующими свойствами: — несмещенная оценка с большой дисперсией; — оценка с небольшим смещением, но сравнительно малой дисперсией. В данном случае более предпочтительной будет оценка , поскольку ее значения, вычисленные по различным выборкам (теоретически возможным при повторениях наблюдений), будут чаще оказываться в окрестности истинного значения параметра . Данный пример подчеркивает важную роль дисперсии оценки как измерителя качества оценивания.

1.4.3. Наилучшая несмещенная оценка

Как было показано выше, решение О Том, какой метод оценивания «лучше», должно основываться на рассмотрении не только математических ожиданий оценок, но и их дисперсий. Однако говорить об оценке с «минимально возможной> дисперсией следует с осторожностью.
Предположим, например, что для оценки параметра в модели (1.15) Используется оценка =123,4 , принимающая одно и то же значение вне зависимости от содержательного смысла задачи или имеющихся выборочных данных. Поскольку эта оценка не меняется, ее дисперсия равна нулю наименьшему из возможных значений. По этой причине, очевидно, необходимо ограничить поиск минимальной дисперсии каким-либо классом оценок. Обычно это достигается за счет рассмотрения только несмещенных оценок.
Рассмотрим две несмещенные оценки, одна из которых () Имеет распределение с меньшей дисперсией, чем другая оценка (). Ясно, что более приемлем метод оценивания по формуле , так как она чаще будет давать оценку, близкую к истинному значению оцениваемого параметра, чем .

Оценка, которая имеет наименьшую дисперсию среди оценок некоторого класса, называется Наиболее эффективной Или Наилучшей В этом классе.

Вообще говоря, существует общий подход к выбору оценок — Принцип максимального правдоподобия, Использование которого во многих ситуациях позволяет получать наилучшую несмещенную оценку, если она существует. Однако часто бывает удобно ограничиться рассмотрением оценок, являющихся линейными функциями ошибок. Оценка, которая является Линейной, Несмещенной и имеет наименьшую дисперсию среди всех линейных несмещенных оценок, называется Наилучшей линейной несмещенной оценкой.

Если мы оцениваем более чем один параметр, то понятие эффективности необходимо уточнить. При наличии двух оценок и K-мерного векторного параметра обычно сравнивают ковариационные матрицы этих оценок, имеющие размерности K K. Если разность ковариационных матриц Var() — Var() неотрицательно
определена, то говорят, что векторная оценка является более эффективной, чем .

1.4.4. Асиiiптотические свойства оценок

Следует подчеркнуть, что рассмотренные выше теоретические свойства «хорошей» оценки (несмещенность, эффективность) должны выполняться при любом фиксированном объеме выборочных наблюдений, используемых при ее вычислении. Так, например, математическое ожидание несмещенной оценки должно совпадать с оцениваемым параметром вне зависимости от количества имеющихся наблюдений. Однако во многих случаях оценка с такими свойствами не существует. Тогда следует обратиться К асимптотическим Свойствам оценки, т. е. посмотреть, как она ведет себя, когда используется очень большое (неограниченно растущее) количество выборочных наблюдений. Иногда, если известны только асимптотические свойства рассматриваемой оценки, ее поведение при малых объемах выборки исследуют путем имитации подходящего механизма получения данных с помощью метода Монте-Карло.
Интуитивное представление о том, чем занимается асимптотическая теория, можно получить с помощью все тех же экспериментов Монте-Карло. Пусть данные формируются в соответствии с уравнением (1.15) При заданном значении параметра , причем объясняющая переменная х имеет неслучайный характер (например, является временем) и, таким образом, список ее значений заранее известен и фиксирован. При заданном объеме выборки Т Первый шаг процедуры Монте-Карло состоит в генерации последовательности значений случайных ошибок , t = ( 1, 2, …, Т И соответствующих значений зависимой переменной . На втором шаге по полученным данным и известной формуле оценочной функции вычисляется значение оценки параметра . Многократное повторение этой двух шаговой процедуры (при одном и том же объеме выборки Т) позволит получить достаточно длинную серию реализаций оценки и построить по ней гистограмму распределения этой оценки.

Изложенная процедура многократной генерации временных рядов и у определенной длины Т с последующим вычислением гистограммы распределения оценки может быть реализована для некоторого начального значения Т = Т0, например, для 100 наблюдений. Далее такие же эксперименты Монте-Карло можно повторить для Т = Т0 + 1, затем для Т = Т0 + 2 и так далее, увеличивая Т. При каждом значении Т будет получено отдельное эмпирическое распределение, соответствующее оценке . Если свойства оценки не зависят от объема выборки Т, то гистограммы распределений будут выглядеть практически одинаково. Если же объем выборки сказывается на поведении оценки, то вид распределений (их форма и/или положение) будет меняться при росте Т.

Осуществление подобных компьютерных экспериментов необходимо далеко не всегда. Во многих случаях поведение оценок при больших Т можно исследовать математически. Свойства оценок, полученные при , называются асимптотическими свойствами.

Как мы упоминали ранее, форма и положение эмпирического распределения для малых значений Т может рассматриваться для того, чтобы проверить свойства оценки при малом объеме выборки, если они не могут быть получены математически. Заметим, что последовательность , T=T0, Т0 + 1, Т0 + 2 …, где обозначает оценку (формулу для оценивания), вычисляемую по выборке объема Т, сама является случайным процессом, так как каждый член этой последовательности — случайная величина, принимающая те или иные значения в зависимости от конкретной реализации наблюдаемых временных рядов.

Предел распределения оценки, если он существует, при стремлении Т к бесконечности, называется асимптотическим распре делением оценки. Если математическое ожидание оценки стремится к истинному значению оцениваемого параметра, то оценка называется асимптотически несмещенной. Однако чаще нас будет интересовать другое асимптотическое свойство — состоятельность. Образно говоря, оценка называется состоятельной, если по мере увеличения числа наблюдений Т Значения (распределение значений) оценки все сильнее концентрируются вокруг истинного значения параметра. Формально Состоятельность Означает, что вероятность того, что разность между значением оценки и истинным значением параметра превзойдет произвольно заданную (сколь угодно малую) величину, должна стремиться к нулю при стремлении объема выборки к бесконечности:

(1.17)

Если оценка состоятельна, т. е. для нее выполняется предельное соотношение (1.17), То говорят, что ее Предел по вероятности Равен истинному значению оцениваемого параметра, и пишут

(1.18)

Таким образом, «состоятельность» и «сходимость по вероятности» — это синонимы.
Если оценивается вектор параметров, то оценка считается состоятельной, если каждая компонента вектора оценок сходится по вероятности к соответствующей компоненте вектора истинных значений параметров.
Пусть имеется две оценки, вычисляемые по выборке объема Т, и такие, что наряду с соотношением (1.18) Выполняется также

(1.19)

Тогда справедливы следующие свойства пределов по вероятности:

Если — константа, то

(1.20,е)

Если — непрерывная функция, то

(1.20,F)

Утверждение (1.20,F) называется теоремой Слуцкого. Оно справедливо не только в случае одного числового параметра , но и если — вектор. Тогда — непрерывная функция соответствующего числа аргументов. Легко заметить, что свойства (1.20, а), (1.20, b), (1.20, c) и (1.20, d) являются следствиями теоремы Слуцкого.

Следует обратить внимание на различия между понятиями математического ожидания и дисперсии асимптотического распределения оценки при Т , пределами математического ожидания и дисперсии оценки при Т и пределом по вероятности оценки при Т.

В некоторых случаях пределы математического ожидания и дисперсии оценки при Т могут не существовать, в то время как математическое ожидание и дисперсия асимптотического распределения существуют, поэтому использование моментов асимптотического распределения считается более удобным.

Достаточное условие состоятельности оценки состоит в том, чтобы среднее асимптотического распределения было равно истинному значению параметра и дисперсия асимптотического распределения равнялась нулю. Приведем пример, показывающий, что это условие не является необходимым.

Предположим, что распределение оценки при фиксированном объеме выборки Т с вероятностью, практически равной единице, концентрируется в малой окрестности точки , а с оставшейся (почти нулевой) вероятностью может принимать значения близкие к Т. Точнее, пусть

и

Для простоты дальнейших выкладок будем дополнительно считать, что оценка имеет функцию плотности, которая принимает значение Т — 1 на отрезке длины 1/Т с центром в. т. очке , значение 1 на отрезке длины 1/Т с центром в точке Т и значение 0 в остальных случаях. Ясно, что такая оценка является состоятельной, так как

при . в результате прямых вычислений нетрудно получить следующие результаты:

и

Таким образом, предел математического ожидания оценки не совпадает с истинным значением оцениваемого параметра (асимптотической несмещенность нет) и, более того, асимптотически дисперсия оценки бесконечно велика, тем не менее оценка является состоятельной.