Каким свойством пространства обуславливается закон сохранения импульса

В предыдущих разделах рассмотрены три фундаментальных закона природы: закон сохранения импульса, момента импульса и энергии. Следует
понимать, что эти законы выполняются только в инерциальных системах отсчета.
В самом деле, при выводе этих законов мы пользовались вторым и третьим законами Ньютона, а они применимы только в инерциальных
системах. Напомним также, что импульс и момент импульса сохраняются в том случае, если система замкнутая (сумма всех внешних сил и
всех моментов сил равна нулю). Для сохранения же энергии тела условия замкнутости недостаточно – тело должно быть еще и адиабатически
изолированным (т.е. не участвовать в теплообмене).
Во всей истории развития физики законы сохранения оказались чуть ли не единственными законами, сохранившими свое значение при
замене одних теорий другими. Эти законы тесно связаны с основными свойствами пространства и времени.
равнозначность всех моментов времени (симметрия по отношению к сдвигу начала отсчета времени). Равнозначность следует понимать в
том смысле, что замена момента времени t1 на момент времени t2, без изменения значений
координат и скорости частиц, не изменяет механические свойства системы. Это означает то, что после указанной замены, координаты
и скорости частиц имеют в любой момент времени t2 + t такие же значения, какие имели
до замены, в момент времени t1 + t.
одинаковость свойств пространства во всех точках (симметрия по отношению к сдвигу начала координат). Одинаковость следует понимать
в том смысле, что параллельный перенос замкнутой системы из одного места пространства в другое, без изменения взаимного расположения
и скоростей частиц, не изменяет механические свойства системы.
одинаковость свойств пространства по всем направлениям (симметрия по отношению к повороту осей координат). Одинаковость следует
понимать в том смысле, что поворот замкнутой системы, как целого, не отражается на её механических свойствах.
Между законами типа основного уравнения динамики и законами сохранения имеется принципиальная разница. Законы динамики дают нам
представление о детальном ходе процесса. Так, если задана сила, действующая на материальную точку и начальные условия, то можно
найти закон движения, траекторию, величину и направление скорости в любой момент времени и т. п. Законы же сохранения не дают
нам прямых указаний на то, как должен идти тот или иной процесс. Они говорят лишь о том, какие процессы запрещены и потому в
природе не происходят.
Таким образом, законы сохранения проявляются как принципы запрета: любое явление, при котором не выполняется хотя бы один из
законов сохранения, запрещено, и в природе такие явления никогда не наблюдаются. Всякое явление, при котором не нарушается ни
один из законов сохранения, в принципе может происходить.
Рассмотрим следующий пример. Может ли покоящееся тело за счет внутренней энергии начать двигаться? Этот процесс не противоречит
закону сохранения энергии. Нужно лишь, чтобы возникающая кинетическая энергия точно равнялась убыли внутренней энергии.
На самом деле такой процесс никогда не происходит, ибо он противоречит закону сохранения импульса. Раз тело покоилось, то его
импульс был равен нулю. А если оно станет двигаться, то его импульс сам собой увеличится, что невозможно. Поэтому внутренняя
энергия тела не может превратиться в кинетическую, если тело не распадётся на части.
Если же допустить возможность распада этого тела на части, то запрет, налагаемый законом сохранения импульса, снимается. При этом
возникшие осколки могут двигаться так, чтобы их центр масс оставался в покое, – а только этого и требует закон сохранения импульса.
Итак, для того чтобы внутренняя энергия покоящегося тела могла превратиться в кинетическую, это тело должно распасться на части.
Если же есть еще один какой-либо закон, запрещающий распад этого тела на части, то его внутренняя энергия и масса покоя будут
постоянными величинами.
Фундаментальность законов сохранения заключается в их универсальности. Они справедливы при изучении любых физических
процессов (механических, тепловых, электромагнитных и др.). Они одинаково применимы в релятивистском и нерелятивистском движении,
в микромире, где справедливы квантовые представления, и в макромире, с его классическими представлениями.
Источник
Рассмотрим изменение импульсов тел при их взаимодействии друг с другом.
Если два или несколько тел взаимодействуют только между собой (то есть не подвергаются воздействию внешних сил), то эти тела образуют замкнутую систему.
Импульс, равный векторной сумме импульсов тел, входящих в замкнутую систему, называется суммарным импульсом этой системы.
Таким образом, чтобы найти суммарный импульс замкнутой системы (n) тел, необходимо найти векторную сумму импульсов всех тел, входящих в данную систему:
pсум→=p1→+p2→+…+pn→.
Импульс каждого из тел, входящих в замкнутую систему, может меняться в результате их взаимодействия друг с другом.
Векторная сумма импульсов тел, составляющих замкнутую систему, не меняется с течением времени при любых движениях и взаимодействиях этих тел.
В этом заключается закон сохранения импульса, который называют также законом сохранения количества движения.
Закон сохранения импульса впервые был сформулирован Р. Декартом. В одном из своих писем он написал:
«Я принимаю, что во Вселенной, во всей созданной материи есть известное количество движения, которое никогда не увеличивается, не уменьшается, и, таким образом, если одно тело приводит в движение другое, то теряет столько своего движения, сколько его сообщает».
Рассмотрим систему, состоящую только из двух тел — шаров массами m1 и m2, которые движутся прямолинейно навстречу друг другу со скоростями v1 и v2. Шары обладают импульсами p1→=m1v1→ и p2→=m2v2→ соответственно.
Через некоторое время шары столкнутся. Во время столкновения, длящегося в течение очень короткого промежутка времени (t), возникнут силы взаимодействия F1→ и F2→, приложенные соответственно к первому и второму шару. В результате действия этих сил скорости шаров изменятся. Обозначим скорости шаров после соударения v1′ и v2′. И импульсы шаров станут p1→′=m1v1→′ и p2→′=m2v2→′ соответственно.
Тогда, согласно закону сохранения импульса, имеют место равенства:
или
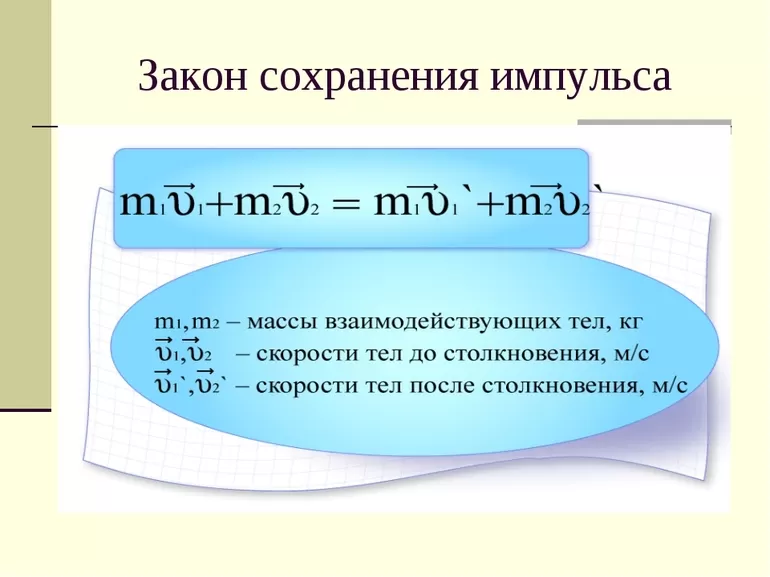
m1v1→+m2v2→=m1v1→′+m2v2→′.
Данные равенства являются математической записью закона сохранения импульса.
Закон сохранения импульса выполняется и в том случае, если на тела системы действуют внешние силы, векторная сумма которых равна нулю.
Таким образом, более точно закон сохранения импульса формулируется так:
векторная сумма импульсов всех тел замкнутой системы — величина постоянная, если внешние силы, действующие на неё, отсутствуют, или же их векторная сумма равна нулю.
Импульс системы тел может измениться только в результате действия на систему внешних сил. И тогда закон сохранения импульса действовать не будет.
Пример:
при стрельбе из пушки возникает отдача: снаряд летит вперёд, а само орудие откатывается назад. Почему?
Снаряд и пушка — замкнутая система, в которой действует закон сохранения импульса. В результате выстрела из пушки импульс самой пушки и импульс снаряда изменятся. Но сумма импульсов пушки и находящегося в ней снаряда до выстрела останется равной сумме импульсов откатывающейся пушки и летящего снаряда после выстрела.
Обрати внимание!
В природе замкнутых систем не существует. Но если время действия внешних сил очень мало, например, во время взрыва, выстрела и т. п., то в этом случае воздействием внешних сил на систему пренебрегают, а саму систему рассматривают как замкнутую.
Кроме того, если на систему действуют внешние силы, но сумма их проекций на одну из координатных осей равна нулю (то есть силы уравновешены в направлении этой оси), то в этом направлении закон сохранения импульса выполняется.
Великий учёный Исаак Ньютон изобрёл наглядную демонстрацию закона сохранения импульса — маятник, или её ещё называют «колыбель». Это устройство представляет собой конструкцию из пяти одинаковых металлических шаров, каждый из которых крепится с помощью двух тросов к каркасу, а тот в свою очередь — к прочному основанию П-образной формы.
Маятник Ньютона устроен так, что начальный шар передаёт импульс второму шарику, а затем замирает. Нашему глазу на первый взгляд не заметно, как следующий шарик принимает импульс от предыдущего, мы не можем проследить его скорость. Но, если взглянуть пристальнее, можно заметить, как шарик немножко «вздрагивает». Это объясняется тем, что он совершает движения с посланной ему скоростью, но поскольку расстояние очень маленькое, ему некуда разогнаться, то он может на своём коротком пути передать импульс третьему шарику и в итоге остановиться.
Такое же действие совершает и следующий шарик и т. д. Последнему шарику некуда передавать свой импульс, поэтому он свободно колеблется, поднимаясь на определённую высоту, а затем возвращается, и весь процесс передачи импульсов повторяется в обратном порядке.
Самый яркий пример применения закона сохранения импульса — реактивное движение.
Источники:
Пёрышкин А. В., Гутник Е. М. Физика, 9 кл.: учебник. — М.: Дрофа, 2014. — 319 с.
www.klassnoedelo.ru, сайт «Классное дело — новые технологии в образовании»
www.barvinok80.narod.ru, сайт дошкольного учреждения образования «Барвинок»
www.hottabich.com.ua, сайт «Hottabich»
www.thegreenhead.com, сайт «Green Head»
www.askskb.net, сайт «Интерактивная физика»
Источник
Краткое описание

Импульсом принято называть влияние массы тела на итоговую скорость. На этот случай специалисты разработали следующую формулу: p = m * V. В физике импульс представляет собой некую векторную величину, которая всегда направлена только в одну сторону. Само слово переводится с латинского языка, как «толкать», «двигать». Импульс принято обозначать маленькой буквой р, а вот измеряться он может только в кг*м/с.
Талантливый Рене Декарт был первым человеком, который начал использовать понятие импульс. Он пытался использовать своё открытие как определённую величину, которая заземляет силу. Причина такого подхода Рене весьма очевидна. Измерить единицу силы крайне тяжело, а вот узнать скорость и массу — это задача более простая и выполнимая. Именно поэтому в физике часто говорят, что импульс — это не что другое, как количество движения. Система материальных точек называется замкнутой, если внешние силы отсутствуют, или их равнодействующий показатель равен нулю.
Чтобы можно было разобраться в том, при каких условиях выполняется закон сохранения импульсов, нужно понять, что это физическое направление лежит в основе такого весьма удивительного явления как реактивное движение. Последнее получило широкое применение не только в технике, но и живой природе. Кальмары, осьминоги и медузы отлично используют реактивное движение, которое позволяет им преодолевать большие расстояния в своём подводном мире.
А вот в технике это физическое явление применяется в самолётах, ракетах и даже космических кораблях. Отдельного внимания заслуживает импульс в релятивистской механике. А всё потому, что законы сохранения механической энергии и импульса применяются для решения задач о движении тел после столкновения.
Ключевые особенности

Активно используемый в современном мире закон о сохранении обычных импульсов является следствием из второго и третьего законов Ньютона. Для лучшего усвоения этой темы лучше рассмотреть характерный пример. Специалистами была взята замкнутая система сразу из двух взаимодействующих между собой тел, которые отобразили при помощи F1 и F2. В третьем законе Ньютона чётко написано, что F2 = -F1. Тела взаимодействуют друг с другом в течение определённого промежутка времени (t).
В такой ситуации импульсы сил остаются идентичными по модулю, но противоположными по своему направлению (F1t = -F1t).
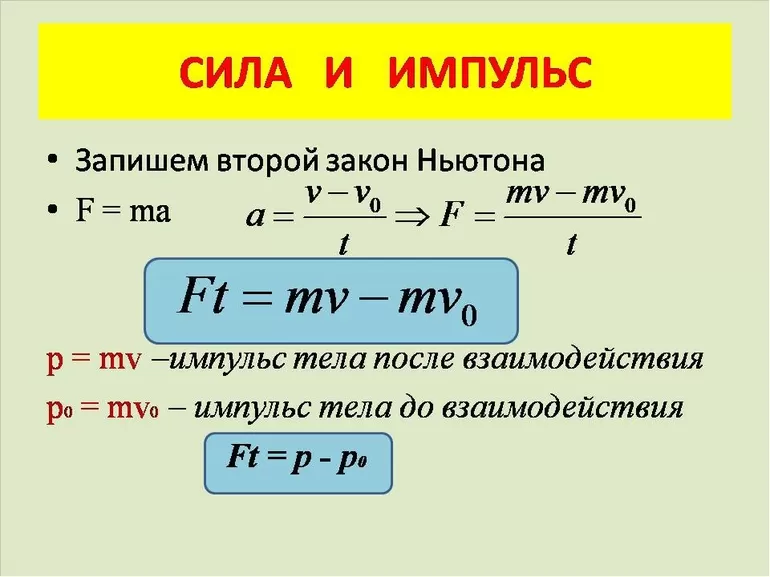
Если применить второй закон Ньютона, то в итоге обязательно получиться вот такое математическое выражение: F1t = m1v1 — m1v1; F2t = m1v2 — m1v2. Для отображения реальной скорости тел в конце взаимодействия используются символы v1 и v2. Из этого можно сделать вывод, что соотношение двух тел будет выглядеть следующим образом: m1v1 + m2v2 = m1v1 + m2v2.
Полученный результат позволяет говорить о равенстве (математическая форма записи закона). Это значит, что первоначальный показатель под воздействием какой-либо силы не изменится. Необходимо запомнить, что определение закона сохранения обязательно выполняется и для проекций векторов на координатные оси. Если следовать всем правилам, то можно легко определить суммарный результат в поставленной задаче, а также находить реальную скорость тел, не зная показателей действующих сил.
В качестве примера также можно рассмотреть снаряд, который вылетает из пушки. Эта задача элементарная, но очень познавательная. В роли взаимодействующих тел выступает пушка и снаряд. На первом этапе оба объекта остаются неподвижными. Но при выстреле снаряд приобретает скорость v и летит только вперёд. А вот пушка откатывается в противоположную сторону со скоростью V (происходит отдача, которая может зависеть только от выстрела). В соответствии с законом в проекции на ось можно записать:
- mv-MV=0;
- V=mv/N.
На этом примере можно увидеть, что всё элементарно и просто. При движении электронов и других субатомных частиц изменение их состояния происходит скачком без пребывания в промежуточных состояниях. Эту тему активно изучают в 9 классе
Интересные факты
При изучении этой темы нужно понимать, что закон о сохранности импульсов остаётся актуальным исключительно в изолированной/ замкнутой физической системе. В этом случае речь касается той отрасли, где абсолютно все тела тесно взаимодействуют между собой и не реагируют на внешние факторы. Но даже в этом случае действуют свои правила. Лучше представить замкнутую систему, которая состоит из двух физических тел. В этом случае возникают внутренние силы, которые могут характеризоваться определёнными параметрами.
Для первого тела импульс будет равен следующей формуле: Ft = m1v1 — m1v1. В действие снова вступает третий закон Ньютона, описываемый то, что все воздействующие на тела силы равны по своей величине, но противоположны по направлению. А это значит, что для второго тела будет действовать немного другая формула: — Ft = m1v2 — m1v2.
Поиск верного решения происходит путём элементарных вычислений, за счёт чего в итоге получаем математическую формулу закона сохранения импульса: m1v1 + m2v2 = m1v1l + m2v2l. Расшифровка выглядит следующим образом:
- v 1l и v 2l — скорость двух тел;
- p 1 ‘= m 1 · v 1 ‘ — импульс после взаимодействия;
- m 1 и m 2 — масса тел;
- p 2 = m 2 · v 2 — импульс второго тела до взаимодействия;
- v 1 и v 2 — скорость до взаимодействия;
- p 2 ‘= m 2 · v 2 ‘ — после взаимодействия;
- p 1 = m 1 · v 1 — импульс первого тела до взаимодействия.

Для каждого параметра свойственны свои характеристики, но все они тесно связаны между собой. Векторная сумма импульсов тел до их фактического взаимодействия идентична векторной сумме после взаимодействия. Пример: после выстрела из обычного ружья импульс оружия и пули изменится. Но вот итоговая сумма импульсов останется равной.
Более точную формулировку закона дали физики, так как они утверждают, что векторная сумма импульсов всех тел в замкнутой системе представляет собой постоянную величину, но только в том случае, воздействующие внешние силы полностью отсутствуют либо векторная сумма была приравнена к нулю. Безусловно, в природе замкнутых систем не существует. Если внешние силы воздействовали на тела в течение короткого промежутка времени, то в такой ситуации можно оставить всё без изменений, а саму систему рассматривать как замкнутую.
Основополагающие моменты
На нашей планете не существует замкнутых систем. Но если суммарные действия внешних сил меньше минимума (к примеру: во время взрыва), то имеющимся воздействием внешних сил предпочитают пренебрегать, из-за чего система приобретает статус замкнутой. Эксперты также придерживаются того мнения, что если воздействие внешних сил всё же присутствует, но итоговая их сумма проекций на одну из координатных осей равна нулю, то в этом направлении закон сохранения образуемых импульсов остаётся актуальным.

Талантливый учёный Исаак Ньютон в своё время изобрёл действительно отличное приспособление, которое как можно лучше демонстрирует сохранность импульса — маятник (колыбель). Это устройство представляет собой небольшую конструкцию, состоящую из 5 одинаковых металлических шаров, каждый из которых прикреплён к каркасу при помощи двух тросов. Основание имеет своеобразную П-образную форму.
Маятник Ньютона построен таким образом, что первый шар передаёт кинетическую энергию второму шарику, а после этого замирает. На первый взгляд, человек может и не заметить, что следующий шар принимает импульс, так как мы не можем проследить его скорость. Но если хорошо присмотреться, то можно увидеть, как шарик немного «вздрагивает» во время столкновения.
Объясняется это явление тем, что он совершает логическое движение с посланной ему скоростью, но так как итоговое расстояние слишком маленькое, ему просто не удаётся должным образом разогнаться. Но он может передать свой импульс уже третьему шарику и в итоге на время остановиться. Совершенно иная ситуация возникает в случае с последним шаром, так как у него нет возможности выполнить упругий удар и передать свой импульс, из-за чего он просто свободно колеблется.
Сущность реактивного движения
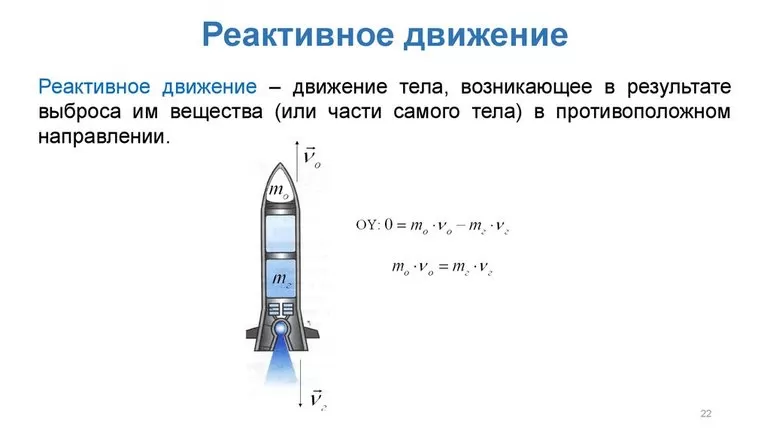
Это физическое явление тоже основано на принципе отдачи. Из сопла реактивного двигателя предварительно нагретые газы выбрасываются наружу со скоростью n. Масса несгоревшего топлива рана m, а вот вес самой ракеты после истечения газов будет обозначаться большой буквой А. В этом случае пример построен на замкнутой системе под названием «ракета-газ».
Из имеющихся данных может легко определяться скорость ракеты С после истечения газов. Все действия происходят в соответствии с формулой: С= mn /А. Ранее рассмотренная формула для пушки с ядром не является актуальной в этом случае, так как она может дать только приблизительные цифры. Всё дело в том, что основная масса газов выходит из специального сопла не сразу, а постепенно.
Масса ракеты в конкретный момент времени (t) равна А, а само устройство движется со скоростью v. В течение определённого промежутка времени ? t из сопел ракеты постепенно выбрасывается газ небольшими порциями с относительной скоростью n. Через некоторое время? t ракета начнёт двигаться со скоростью v +? v. А вот масса устройства станет равной А — ?А. Решение задачи будет выглядеть следующим образом:
- (А-?А)*(v +? v) — импульс ракеты в момент t + ? t.
- ?А*(v + n) — импульс реактивных газов.
- A v = (А−ΔА) ⋅ (v+Δv) + ΔА ⋅ (v+ ? n) — формула, которая соответствует изучаемому закону.
- А Δ v / Δ t = Δ А ⋅ n Δ t (Δ t → 0).
- Aa = − μ u.
В этом случае символом μ μ обозначаем расход задействованного топлива за отведённый промежуток времени. А вот для указания реактивной силы тяги используется сочетание μ u. Направление этой силы максимально совпадает с выбранным направлением движения ракеты. Для расчёта конечной скорости устройства принято использовать формулу: v = nlh (A 0 / A).
Стоит отметить, что

современное ракетостроение шагнуло далеко вперёд, благодаря чему специалисты стремятся развиваться в сторону универсальных многоступенчатых ракет. Своевременный сброс отсеков с уже отработанным топливом позволяет существенно снизить массу агрегата и тем самым максимально оптимизировать дальнейший расход газа для полноценного разгона.
Особенности применения физического явления

Закон сохранения момента импульса весьма удивителен, так как это физическое явление встречается даже в утончённом фигурном катании. А всё дело в том, что раскинув руки в разные стороны и заводя свободную ногу, фигуриста сообщает себе медленное вращение вокруг вертикальной оси. Если резко сгруппироваться, то момент инерции будет снижен, а также произойдёт приращение угловой скорости. Но если ось вращения является свободной, то это не может означать, что в инерциальной системе отсчёта сохраняется прежнее направление угловой скорости.
Если внимательно следить за действиями жонглёра, то в итоге можно заметить, что он передаёт всем подбрасываемым предметам импульс. Только в этом они возвращаются ему в том же положении, которое им было придано изначально. Сохранность импульса важна даже в сфере оружия, так как нарезное орудие даёт большую дальность, нежели гладкоствольное изделие. Выпущенный в один момент артиллерийский снаряд вращается вокруг своей продольной оси, из-за чего его полёт является максимально устойчивым.
Способность сохранять созданный импульс занимает в физике почётное место, так как именно на этом понятии построены фундаментальные законы природы. Если следовать теореме Эмми Нётер, то можно понять, что каждому закону обязательно ставится в соответствие определённая симметрия уравнений, описывающих эту систему. Изучаемый закон эквивалентен однородности пространства. Самый элементарный вывод этого утверждения базируется на применении лагранжева подхода.
Источник
