Каким свойством обладают углы вписанного в окружность

Вписанные и центральные углы
Определение 1. Центральным угломназывают угол, вершина которого совпадает с центром окружности, а стороны являются радиусами радиусами (рис. 1).

Рис. 1
Определение 2. Вписанным углом называют угол, вершина которого лежит на окружности, а стороны являются хордами хордами (рис. 2).

Рис. 2
Напомним, что углы можно измерять в градусах и в радианах. Дуги окружности также можно измерять в градусах и в радианах, что вытекает из следующего определения.
Определение 3. Угловой мерой (угловой величиной) дуги окружности является величина центрального угла, опирающегося на эту дугу.
Теоремы о вписанных и центральных углах
| Фигура | Рисунок | Теорема |
| Вписанный угол |  | Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу. Посмотреть доказательство |
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же дугу равны. |
| Вписанный угол |  | Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды |
| Вписанный угол |  | Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды |
| Вписанный угол |  | Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр |
| Окружность, описанная около прямоугольного треугольника |  | Середина гипотенузы прямоугольного треугольника является центром описанной Посмотреть доказательство |
| Вписанный угол |
Теорема: Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Посмотреть доказательство |
Теорема: Вписанные углы, опирающиеся на одну и ту же дугу равны.
|
Теорема: Вписанные углы, опирающиеся на одну и ту же хорду, равны, если их вершины лежат по одну сторону от этой хорды
|
Теорема: Два вписанных угла, опирающихся на одну и ту же хорду, в сумме составляют 180°, если их вершины лежат по разные стороны от этой хорды
|
Теорема: Вписанный угол является прямым углом, тогда и только тогда, когда он опирается на диаметр
|
| Окружность, описанная около прямоугольного треугольника |
Теорема: Середина гипотенузы прямоугольного треугольника является центром описанной
Посмотреть доказательство |
Теоремы об углах, образованных хордами, касательными и секущими
| Фигура | Рисунок | Теорема | Формула |
| Угол, образованный пересекающимися хордами |  | Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство | |
| Угол, образованный секущими, которые пересекаются вне круга |  | Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство | |
| Угол, образованный касательной и хордой, проходящей через точку касания |  | Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство | |
| Угол, образованный касательной и секущей |  | Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство | |
| Угол, образованный двумя касательными к окружности |  | Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный пересекающимися хордами хордами |
 |
| Формула: |
Теорема Величина угла, образованного пересекающимися хордами, равна половине суммы величин дуг, заключённых между его сторонами. Посмотреть доказательство |
| Угол, образованный секущими секущими, которые пересекаются вне круга |
|
| Формула: |
Теорема Величина угла, образованного секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный касательной и хордой хордой, проходящей через точку касания |
 |
| Формула: |
Теорема Величина угла, образованного касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами Посмотреть доказательство |
| Угол, образованный касательной и секущей касательной и секущей |
|
| Формула: |
Теорема Величина угла, образованного касательной и секущей, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
| Угол, образованный двумя касательными касательными к окружности |
|
| Формулы: |
Теорема Величина угла, образованного двумя касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами Посмотреть доказательство |
Доказательства теорем об углах, связанных с окружностью
Теорема 1. Величина вписанного угла равна половине величины центрального угла, опирающегося на ту же дугу.
Доказательство. Рассмотрим сначала вписанный угол ABC, сторона BC которого является диаметром окружности диаметром окружности, и центральный угол AOC (рис. 5).

Рис. 5
Так как отрезки AO и BO являются радиусами окружности радиусами окружности, то треугольник AOB – равнобедренный, и угол ABO равен углу OAB. Поскольку угол AOC является внешним углом треугольника AOB, то справедливы равенства
Таким образом, в случае, когда одна из сторон вписанного угла проходит через центр окружности, теорема 1 доказана.
Теперь рассмотрим случай, когда центр окружности лежит внутри вписанного угла (рис. 6).

Рис. 6
В этом случае справедливы равенства
и теорема 1 в этом случае доказана.
Осталось рассмотреть случай, когда центр окружности лежит вне вписанного угла (рис. 7).

Рис. 7
В этом случае справедливы равенства
что и завершает доказательство теоремы 1.
Теорема 2. Величина угла, образованного пересекающимися хордами хордами, равна половине суммы величин дуг, заключённых между его сторонами.
Доказательство. Рассмотрим рисунок 8.

Рис. 8
Нас интересует величина угла AED, образованного пересекающимися в точке E хордами AB и CD. Поскольку угол AED – внешний угол треугольника BED, а углы CDB и ABD являются вписанными углами, то справедливы равенства
что и требовалось доказать.
Теорема 3. Величина угла, образованного секущими секущими, пересекающимися вне круга, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство. Рассмотрим рисунок 9.


Рис. 9
Нас интересует величина угла BED, образованного пересекающимися в точке E секущими AB и CD. Поскольку угол ADC – внешний угол треугольника ADE, а углы ADC , DCB и DAB являются вписанными углами, то справедливы равенства
что и требовалось доказать.
Теорема 4. Величина угла, образованного касательной и хордой касательной и хордой, проходящей через точку касания, равна половине величины дуги, заключённой между его сторонами.
Доказательство. Рассмотрим рисунок 10.


Рис. 10
Нас интересует величина угла BAC , образованного касательной AB и хордой AC . Поскольку AD – диаметр диаметр, проходящий через точку касания, а угол ACD – вписанный угол, опирающийся на диаметр, то углы DAB и DCA – прямые. Поэтому справедливы равенства
что и требовалось доказать
Теорема 5. Величина угла, образованного касательной и секущей касательной и секущей, равна половине разности величин дуг, заключённых между сторонами этого угла.
Доказательство. Рассмотрим рисунок 11.


Рис. 11
Нас интересует величина угла BED, образованного касательной AB и секущей CD. Заметим, что угол BDC – внешний угол треугольника DBE, а углы BDC и BCD являются вписанными углами. Кроме того, углы DBE и DCB, в силу теоремы 4, равны. Поэтому справедливы равенства
что и требовалось доказать.
Теорема 6.Величина угла, образованного двумя касательными к окружности касательными к окружности, равна половине разности величин дуг, заключённых между его сторонами.
Доказательство. Рассмотрим рисунок 12.


Рис. 12
Нас интересует величина угла BED, образованного касательными AB и CD. Заметим, что углы BOD и BED в сумме составляют π радиан. Поэтому справедливо равенство
α = π – γ .
Далее получаем
что и требовалось доказать.
На нашем сайте можно также ознакомиться нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Источник
Центральный угол и вписанный угол
Окружность — замкнутая линия, все точки которой равноудалены от ее центра.
Определение центрального угла:
Центральный угол — это угол, вершина которого лежит в центре окружности.
Центральный угол равен градусной мере дуги, на которую он опирается.
На рисунке: центральный угол окружности EOF и дуга, на которую он опирается EF
Определение вписанного угла:
Вписанный угол — это угол, вершина которого лежит на окружности.
Вписанный угол равен половине центрального угла, опирающегося на ту же дугу, что и вписанный угол.
На рисунке: вписанный в окружность угол ABC и дуга, на которую он опирается AC
Свойства центральных и вписанных углов
Углы просты только на первый взгляд. Свойства центрального угла и свойства вписанного угла помогут решать задачки легко и быстро.
- Вписанный угол в два раза меньше, чем центральный угол, если они опираются на одну и ту же дугу:
Угол AOC и угол ABC, вписанный в окружность, опираются на дугу AC, в этом случае центральный угол равен дуге AC, а угол угол ABC равен половине угла AOC.
- Теорема о центральном угле: центральный угол равен градусной мере дуги, на которую он опирается:
ㄥAOB = ◡ AB
- Вписанные углы окружности равны друг другу, если опираются на одну дугу:
ㄥADC = ㄥABC = ㄥAEC, поскольку все три угла, вписанные в окружность, опираются на одну дугу AC.
- Вписанный в окружность угол, опирающийся на диаметр, — всегда прямой:
ㄥACB опирается на диаметр и на дугу AB, диаметр делит окружность на две равные части. Значит дуга AB = 180 ํ, ㄥCAB угол равен половине дуги, на которую он опирается, значит ㄥCAB = 90 ํ.
Если есть вписанный, обязательно найдется и описанный угол. Описанный угол — это угол, образованный двумя касательными к окружности. Вот так:
На рисунке: ㄥCAB, образованный двумя касательными к окружности. AO — биссектриса ㄥCAB, значит центр окружности лежит на биссектрисе описанного угла.
- Градусная мера вписанного угла равна половине градусной меры дуги, на которую он опирается и половине градусной меры центрального угла, опирающегося на эту же дугу.
Для решения задачек мало знать, какой угол называется вписанным, а какой — описанным. Нужно знать, что такое хорда и ее свойство.
Хорда — отрезок, соединяющий две точки на окружности.
- Если две хорды в окружности пересекаются, то произведения отрезков одной равно произведению отрезков другой.
AB * AC = AE * AD
Получается, что стороны вписанного в окружность угла — это хорды.
- Если вписанные углы опираются на одну и ту же хорду — они равны, если их вершины находятся по одну сторону от хорды.
ㄥBAC = ㄥCAB, поскольку лежат на хорде BC.
- Если два вписанных угла опираются на одну и ту же хорду, то их суммарная градусная мера равна 180°, если их вершины находятся по разные стороны от хорды.
ㄥBAC + ㄥBDC = 180°
Примеры решения задач
Центральный, вписанные и описанные углы, как и любые другие, требуют тренировок в решении. Рассмотрите примеры решения задач и потренируйтесь самостоятельно.
Задачка 1. Дана окружность, дуга AC = 200°, дуга BC = 80°. Найдите, чему равен вписанный угол, опирающийся на дугу. ㄥACB = ?
Как решаем: окружность 360° – AC – CB = 360 – 200 – 80 = 80
По теореме: вписанный угол равен дуге ½.
ㄥACB = ½ AB = 40°
Задачка 2. Дана окружность, ㄥAOC = 140°, найдите, чему равна величина вписанного угла.
Мы уже потренировались и знаем, как найти вписанный угол.
На рисунке в окружности центральный угол и дуга AC = 140°
Мы знаем, что вписанный угол равен половине центрального, то ㄥABC = ½ AC = 140/2 = 70°
Задачка 3. Чему равен вписанный в окружность угол, опирающийся на дугу, если эта дуга = ⅕ окружности?
СB = ⅕ от 360 = 72°
Вписанный угол равен половине дуги, поэтому CAB = ½ от CB = 72/36 = 36°
Еще больше примеров и задачек на уроках математики в онлайн-школе Skysmart. Наши преподаватели объяснят любую, даже самую остроугольную тему. Ребенка ждут захватывающие примеры в интерактивном формате, карта прогресса в личном кабинете и даже онлайн-доска, на которой можно чертить вместе с учителем.
Записывайтесь на бесплатный вводный урок математики и занимайтесь в удовольствие!
Источник
Цели и задачи:
- знать определения вписанного и центрального углов, знать теорему о вписанном угле, уметь решать задачи нахождение вписанных, центральных углов и дуг на которые опираются эти углы;
- формирование пространственного мышления;
- воспитание самостоятельности.
Ход урока
I. Организационный момент.
На прошлом уроке мы познакомились с понятиями вписанного угла и центрального угла, с теоремой о вписанном угле. Сегодня мы будем применять эти знания для решения задач.
II. Устный счет.
слайд 1.
- Закончите предложение.
- Центральный угол – это… (угол с вершиной в центре окружности).
- Градусная мера дуги – это… (градусная мера соответствующего центрального угла).
- Угол, вписанный в окружность, – это…(угол, вершина которого лежит на окружности, стороны пересекают ее).
- Угол, вписанный в окружность, равен…(половине соответствующего центрального угла).
- Вписанные углы, опирающиеся на одну и ту же дугу…(равны)
- Вписанные углы, опирающиеся на диаметр… (прямые).
- На доске на рисунке показать и назвать углы и дуги, на которые эти углы опираются.
Рисунок 1.
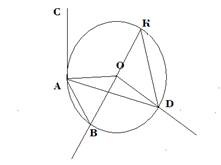
- центральный угол, ответ: ∠АОD, ∠АОВ, ∠ВОD, ∠КОD, ∠ВОК, ∠АОК.
- вписанный угол, ответ: ∠ВКD, ∠АDК, ∠ВАD
- вписанные углы, опирающиеся на одну и ту же дугу, ответ: ∠ВКD и ∠ВАD
III. Проверка домашнего задания.
Проверить и разобрать решение задач №71 и №72 из рабочей тетради к учебнику геометрии.
слайд 2.
№71. Начертите окружность и проведите ее радиусы ОА, ОВ и ОС так, чтобы углы АОВ, ВОС и СОА были равны. Вычислите градусные меры образовавшихся дуг АВ, ВС и СА.
Устно разобрать, чему равны градусные меры получившихся дуг.
АВ=ВС= АС =120°.
№77. Точки М, К и Р делят окружность на дуги, градусные меры которых пропорциональны числам 3, 2 и 7 (считая от точки М к точке К). Вычислите градусные меры углов треугольника МКР.
В рабочей тетради в решении дается подсказка: принимаем градусные меры дуг за 3х°, 2х° и __, что подставили? (7х°).
Так как сумма их градусных мер равна 360°, составим уравнение ____________
Какое уравнение получили?
Проверили решение уравнения.
3х+2х+7х=360
12х=360
х=360:12
х=30
МК=3х=90, РК=2х=60, МР=7х=210
Используя свойство вписанных углов, находим величины углов треугольника МКР:
∠ Р=45°, ∠ М=30°, ∠К=105°.
IV. Решение задач
1. Задачи по чертежам. слайд 3:
- Решите задачи устно найдите х:
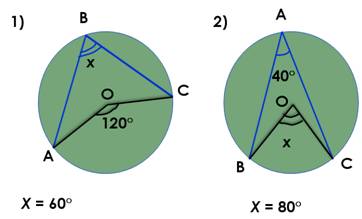
Разобрать, почему в задаче 1 x= 60°, а в задаче 2 x = 80°.
На основании какого свойства? ( свойство вписанного угла: угол, вписанный в окружность, равен половине соответствующего центрального угла).
Постройте в тетради четыре одинаковых окружности.
- Скопируйте задания с рисунков в тетрадь и по данным задач 3 и 4. Презентация слайд 4. См. рисунок 3, найдите х.
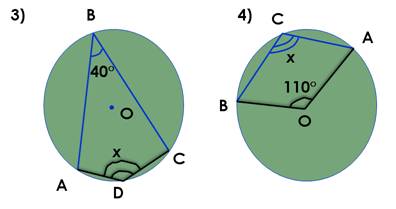
Решение задачи 3: 360° – 80° = 280°,
x = 280°:2 = 140°
Решение задачи 4: 360° – 110° = 250°,
x = 250°:2 = 125°
- Скопируйте задания с рисунков в тетрадь и по данным задач 5 и 6. слайд 5. См. рисунок 4 найдите х.
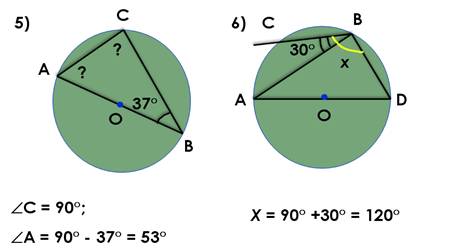
Решение задачи 5: ∠С = 90°,
Какое свойство вписанного угла применяем?
(Вписанные углы, опирающиеся на диаметр прямые)
∠А = 90° – 37°= 53°.
Решение задачи 6: в треугольнике АВD∠В = 90°, ∠CВD =30° + 90° = 120°.
2) Задача №79 в рабочей тетради.
Около равнобедренного треугольника АВС описана окружность. Его основание АС стягивает дугу, градусная мера которой равна 140°. Вычислите градусные меры всех углов треугольника АВС.
В рабочей тетради построили чертеж к задаче Рисунок 7.
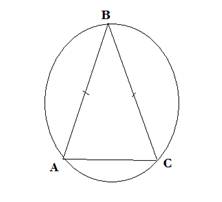
Решение.
Какой угол треугольника АВС можно найти?
Можно найти ∠B, т.к. это вписанный угол, который опирается на дугу АС.
∠В = 140°:2 = 70°,
Какое свойство равнобедренного треугольника можно применить?
В равнобедренном треугольнике углы при основании равны.
∠А = ∠С = (180° – 70°) : 2 = 110°:2 = 55°.
Ответ: ∠В = 70°, ∠А = ∠С = 55°.
V. Домашнее задание.
П.107, повторить теорию по теме «Углы, вписанные в окружность»
Решить задачи №80, 82 в рабочей тетради.
VI. Самостоятельная работа на карточках по готовым чертежам.
слайд 6.
Учащиеся получают карточки с заданиями. См. рисунок 5.
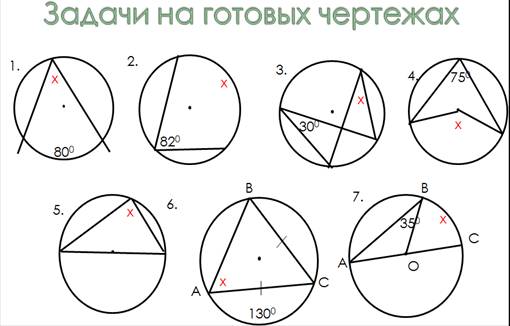
VII. Проверка самостоятельной работы.
слайд 7.
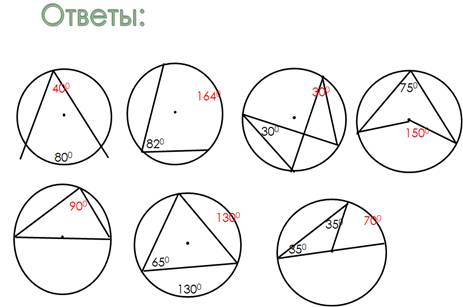
VIII. Итоги урока.
Приложение.
Источник
Мы видели, что вокруг всякого треугольника можно описать окружность.
То есть, для всякого треугольника найдётся такая окружность, что все три вершины треугольника «сидят» на ней. Вот так:
Вопрос: а можно ли то же самое сказать о четырехугольнике? Правда ли, что всегда найдётся окружность, на которой будут «сидеть» все четыре вершины четырехугольника?
Сейчас мы это выясним!
Вот оказывается, что это НЕПРАВДА!
НЕ ВСЕГДА четырехугольник можно вписать в окружность. Есть очень важное условие:
Четырехугольник можно вписать в окружность тогда и только тогда, когда сумма двух его противоположных углов равна ( displaystyle 180{}^circ ).
На нашем рисунке:
( displaystyle alpha +beta =180{}^circ )
Посмотри, углы ( displaystyle alpha ) и ( displaystyle beta ) лежат друг напротив друга, значит, они противоположные. А что же тогда с углами ( displaystyle varphi ) и ( displaystyle psi )? Они вроде бы тоже противоположные?
Можно ли вместо углов ( displaystyle alpha ) и ( displaystyle beta ) взять углы ( displaystyle varphi ) и ( displaystyle psi )?
Конечно, можно!
Главное, чтобы у четырехугольника нашлись какие-то два противоположных угла, сумма которых будет ( displaystyle 180{}^circ ).
Оставшиеся два угла тогда сами собой тоже дадут в сумме ( displaystyle 180{}^circ ). Не веришь? Давай убедимся. Смотри:
Пусть ( displaystyle alpha +beta =180{}^circ ). Помнишь ли ты, чему равна сумма всех четырех углов любого четырехугольника? Конечно, ( displaystyle 360{}^circ ).
То есть ( displaystyle alpha +beta +varphi +psi =360{}^circ ) – всегда! ( displaystyle 180{}^circ )
Но ( displaystyle alpha +beta =180{}^circ ), →( displaystyle varphi +psi =360{}^circ -180{}^circ =180{}^circ).
Волшебство прямо!
Так что запомни крепко-накрепко:
Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна ( displaystyle 180{}^circ )
и наоборот:
Если у четырехугольника есть два противоположных угла, сумма которых равна ( displaystyle 180{}^circ ), то такой четырехугольник вписанный.
Доказывать всё это мы здесь не будем (если интересно, заглядывай в следующие уровни теории). Но давай посмотрим, к чему приводит этот замечательный факт о том, что у вписанного четырехугольника сумма противоположных углов равна ( displaystyle 180{}^circ ).
Вот, например, приходит в голову вопрос, а можно ли описать окружность вокруг параллелограмма?
Попробуем сперва «методом тыка»:
Вот как-то не получается.
Теперь применим знание:
Предположим, что нам как-то удалось посадить на параллелограмм ( displaystyle ABCD) окружность. Тогда непременно должно быть: ( displaystyle alpha +beta =180{}^circ ), то есть ( displaystyle angle B+angle D=180{}^circ ).
А теперь вспомним о свойствах параллелограмма: у всякого параллелограмма противоположные углы равны.
То есть ( displaystyle angle B = angle D).
У нас получилось, что
( displaystyle left{ begin{array}{l}angle B=angle D\angle B+angle D=180{}^circ end{array} right.) → ( displaystyle left{ begin{array}{l}angle B=90{}^circ \angle D=90{}^circ end{array} right.)
А что же углы ( displaystyle A) и ( displaystyle C)?
Ну, то же самое конечно.
( displaystyle ABCD) – вписанный → ( displaystyle angle A+angle C=180{}^circ ) → ( displaystyle angle A=90{}^circ )
( displaystyle ABCD) – параллелограмм→ ( displaystyle angle A=angle C) → ( displaystyle angle C=90{}^circ )
Потрясающе, правда? Получилось, что…
Если параллелограмм вписан в окружность, то все его углы равны ( displaystyle 90{}^circ ), то есть это прямоугольник!
И ещё при этом –
Центр окружности совпадает с точкой пересечения диагоналей этого прямоугольника.
Это, так сказать, в качестве бонуса прилагается.
Ну, вот значит, выяснили, что параллелограмм, вписанный в окружность – прямоугольник.
А теперь поговорим о трапеции. Что будет, если трапецию вписать в окружность? А оказывается, будет равнобедренная трапеция.
Почему?
Вот пусть трапеция ( displaystyle ABCD) вписана в окружность.
Тогда опять ( displaystyle angle B+angle D=180{}^circ ), но из-за параллельности прямых ( displaystyle AD) и ( displaystyle BC) ( displaystyle angle B+angle A=180{}^circ ).
Значит, имеем: ( displaystyle left{ begin{array}{l}angle B+angle D=180{}^circ \angle B+angle A=180{}^circ end{array} right.) → ( displaystyle angle D=angle A) → трапеция равнобокая.
Даже проще чем с прямоугольником, правда? Но запомнить нужно твёрдо – пригодиться:
Трапеция, вписанная в окружность – равнобедренная.
Давай ещё раз перечислим самые главные утверждения, касающиеся четырехугольника, вписанного в окружность:
- Четырехугольник вписан в окружность тогда и только тогда, когда сумма двух его противоположных углов равна ( displaystyle 180{}^circ )
- Параллелограмм, вписанный в окружность – непременно прямоугольник и центр окружности совпадает с точкой пересечения диагоналей
- Трапеция, вписанная в окружность – равнобокая
Главная теорема о вписанном четырехугольнике
Известно, что для всякого треугольника существует описанная окружность (это мы доказывали в теме «Описанная окружность»). Что же можно сказать о четырёхугольнике?
Вот, оказывается, что НЕ ВСЯКИЙ четырехугольник можно вписать в окружность, а есть такая теорема:
Четырёхугольник вписан в окружность тогда и только тогда, когда сумма его противоположных углов равна ( displaystyle 180{}^circ ).
На нашем рисунке – ( largedisplaystyle angle alpha +angle beta =180{}^circ )
Давай попробуем понять, почему так? Другими словами, мы сейчас докажем эту теорему.
Но прежде чем доказывать, нужно понять, как устроено само утверждение. Ты заметил в утверждении слова «тогда и только тогда»? Такие слова означают, что вредные математики впихнули два утверждения в одно.
Расшифровываем:
Этот контент доступен после регистрации
Вы также получите доступ к 15 статьям YouClever без ограничений, видеоурокам и другим бесплатным материалам по тарифу “Репетитор”.
1
«Тогда» означает: Если четырехугольник вписан в окружность, то сумма любых двух его противоположных углов равна ( displaystyle 180{}^circ )
2
«Только тогда» означает: Если у четырёхугольника найдутся два противоположных угла, сумма которых равна ( displaystyle 180{}^circ ), то такой четырехугольник можно вписать в окружность
Прямо как у Алисы: «думаю, что говорю» и «говорю, что думаю».
А теперь разбираемся, отчего же верно и 1, и 2?
Пусть четырехугольник ( displaystyle ABCD) вписан в окружность. Отметим её центр ( displaystyle O) и проведём радиусы ( displaystyle OA) и ( displaystyle OC).
Что же получится? Помнишь ли ты, что вписанный угол вдвое меньше соответствующего центрального?
Если помнишь – сейчас применим, а если не очень – загляни в тему «Окружность. Вписанный угол».
Итак,
( displaystyle angle ABC) – вписанный ( displaystyleRightarrow angle ABC=frac{1}{2}cdot angle psi )
( displaystyle angle ADC) – вписанный ( displaystyleRightarrow angle ADC=frac{1}{2}cdot angle varphi )
Но посмотри: ( displaystyle angle varphi +angle psi =360{}^circ )
Значит,
( displaystyle begin{array}{l}angle ABC+angle ADC=frac{1}{2}angle psi +frac{1}{2}angle varphi =\=frac{1}{2}left( angle psi +angle varphi right)=frac{1}{2}cdot 360{}^circ =180{}^circ end{array})
Получаем, что если ( displaystyle ABCD) – вписанный, то
( displaystyle angle alpha +angle beta =180{}^circ )
Ну, и ясно, что ( displaystyle angle A) и ( displaystyle angle C) тоже в сумме составляет ( displaystyle 180{}^circ ). (нужно так же рассмотреть ( displaystyle angle BAD) и ( displaystyle angle BCD)).
Пусть оказалось так, что у четырехугольника ( displaystyle ABCD) сумма каких – то двух противоположных углов равна ( displaystyle 180{}^circ ). Скажем, пусть
( displaystyle angle B+angle D=180{}^circ )
Мы пока не знаем, можем ли описать вокруг него окружность. Но мы точно знаем, что вокруг треугольника ( displaystyle ABC) мы гарантированно окружность описать можем. Так и сделаем это.
Если точка ( displaystyle D) не «села» на окружность, то она неминуемо оказалась или снаружи или внутри.
Рассмотрим оба случая.
Пусть сначала точка ( displaystyle D) – снаружи.
Тогда отрезок ( displaystyle AD) пересекает окружность в какой-то точке ( displaystyle E). Соединим ( displaystyle C) и ( displaystyle E).
Получился вписанный (!) четырехугольник ( displaystyle ABCE).
Про него уже знаем, что сумма его противоположных углов равна ( displaystyle 180{}^circ ), то есть ( displaystyle angle alpha +angle gamma =180{}^circ ), а по условию у нас ( displaystyle angle alpha +angle beta =180{}^circ )
Получается, что должно бы быть так, что ( displaystyle angle beta =angle gamma )
Но это никак не может быть поскольку ( displaystyle angle gamma ) – внешний угол для ( displaystyle Delta DEC) и значит, ( displaystyle angle gamma =angle beta +angle delta )
А внутри?
Этот контент доступен после регистрации
Вы также получите доступ к 15 статьям YouClever без ограничений, видеоурокам и другим бесплатным материалам по тарифу “Репетитор”.
Проделаем похожие действия. Пусть точка ( displaystyle D) внутри.
Тогда продолжение отрезка ( displaystyle AD) пересекает окружность в точке ( displaystyle E).
Снова ( displaystyle ABCE) – вписанный четырехугольник ( displaystyle angle alpha +angle gamma =180{}^circ ).
А по условию ( displaystyle angle alpha +angle beta =180{}^circquad Rightarrow ) должно выполняться ( displaystyle angle beta =angle gamma ), но ( displaystyle angle beta ) – внешний угол для ( displaystyle Delta DEC) и значит, ( displaystyle angle beta =angle gamma +angle delta ).
То есть опять никак не может быть так, что ( displaystyle angle beta =angle gamma ).
То есть точка ( displaystyle D) не может оказаться ни снаружи, ни внутри окружности – значит, она на окружности!
Доказали всю-всю теорему!
Теперь посмотрим, какие же хорошие следствия даёт эта теорема.
Следствие 1
Параллелограмм, вписанный в окружность, может быть только прямоугольником
Доказательство следствия 1
Давай-ка поймём, почему так. Пусть параллелограмм ( displaystyle ABCD) вписан в окружность. Тогда должно выполняться ( displaystyle angle B+angle D=180{}^circ ).
Но из свойств параллелограмма мы знаем, что ( displaystyle angle B=angle D).
То есть
( displaystyle left{ begin{array}{l}angle B+angle D=180{}^circ \angle B=angle Dend{array} right. left{ begin{array}{l}angle B=90{}^circ \angle D=90{}^circ end{array} right.)
И то же самое, естественно, касательно углов ( displaystyle A) и ( displaystyle C).
Вот и получился прямоугольник – все углы по ( displaystyle 90{}^c



