Каким свойством обладают точки биссектрисы угла

2 июня 2018

Сегодня будет очень лёгкий урок. Мы рассмотрим всего один объект — биссектрису угла — и докажем важнейшее её свойство, которое очень пригодится нам в будущем.

Только не надо расслабляться: иногда ученики, желающие получить высокий балл на том же ОГЭ или ЕГЭ, на первом занятии даже не могут точно сформулировать определение биссектрисы.

И вместо того, чтобы заниматься действительно интересными задачами, мы тратим время на такие простые вещи. Поэтому читайте, смотрите — и берите на вооружение.:)

Для начала немного странный вопрос: что такое угол? Правильно: угол — это просто два луча, выходящих из одной точки. Например:

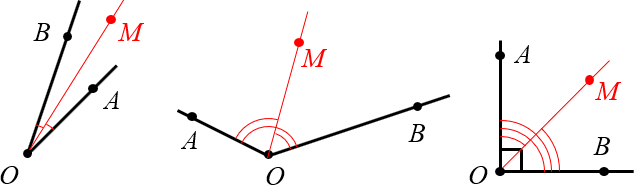
Примеры углов: острый, тупой и прямой

Как видно из картинки, углы могут быть острыми, тупыми, прямыми — это сейчас неважно. Часто для удобства на каждом луче отмечают дополнительную точку и говорят, мол, перед нами угол $AOB$ (записывается как $angle AOB$).

Капитан очевидность как бы намекает, что помимо лучей $OA$ и $OB$ из точки $O$ всегда можно провести ещё кучу лучей. Но среди них будет один особенный — его-то и называют биссектрисой.

Определение. Биссектриса угла — это луч, который выходит из вершины этого угла и делит угол пополам.

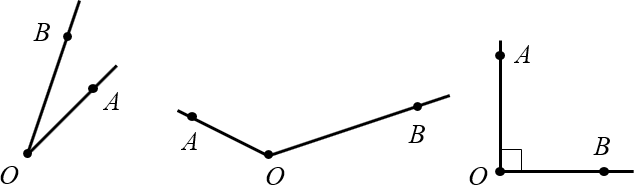
Для приведённых выше углов биссектрисы будут выглядеть так:

Примеры биссектрис для острого, тупого и прямого угла

Поскольку на реальных чертежах далеко не всегда очевидно, что некий луч (в нашем случае это луч $OM$) разбивает исходный угол на два равных, в геометрии принято помечать равные углы одинаковым количеством дуг (у нас на чертеже это 1 дуга для острого угла, две — для тупого, три — для прямого).

Хорошо, с определением разобрались. Теперь нужно понять, какие свойства есть у биссектрисы.

Основное свойство биссектрисы угла

На самом деле у биссектрисы куча свойств. И мы обязательно рассмотрим их в следующем уроке. Но есть одна фишка, которую нужно понять прямо сейчас:

Теорема. Биссектриса угла — это геометрическое место точек, равноудалённых от сторон данного угла.

В переводе с математического на русский это означает сразу два факта:

1. Всякая точка, лежащая на биссектрисе некого угла, находится на одинаковом расстоянии от сторон этого угла.
2. И наоборот: если точка лежит на одинаковом расстоянии от сторон данного угла, то она гарантированно лежит на биссектрисе этого угла.

Прежде чем доказывать эти утверждения, давайте уточним один момент: а что, собственно, называется расстоянием от точки до стороны угла? Здесь нам поможет старое-доброе определение расстояния от точки до прямой:

Определение. Расстояние от точки до прямой — это длина перпендикуляра, проведённого из данной точки к этой прямой.

Например, рассмотрим прямую $l$ и точку $A$, не лежащую на этой прямой. Проведём перпендикуляр $AH$, где $Hin l$. Тогда длина этого перпендикуляра и будет расстоянием от точки $A$ до прямой $l$.

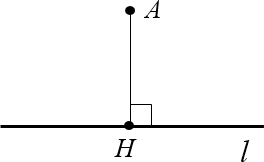Графическое представление расстояния от точки до прямой

Поскольку угол — это просто два луча, а каждый луч — это кусок прямой, легко определить расстояние от точки до сторон угла. Это просто два перпендикуляра:

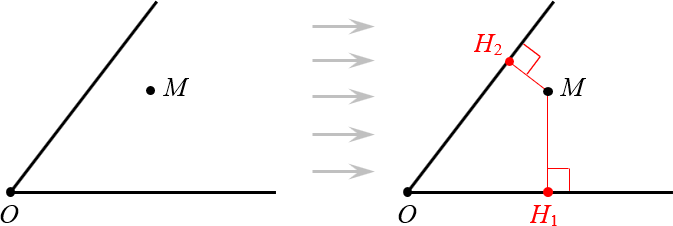Определяем расстояние от точки до сторон угла

Вот и всё! Теперь мы знаем, что такое расстояние и что такое биссектриса. Поэтому можно доказывать основное свойство.

Как и обещал, разобьём доказательство на две части:

1. Расстояния от точки на биссектрисе до сторон угла одинаковы

Рассмотрим произвольный угол с вершиной $O$ и биссектрисой $OM$:

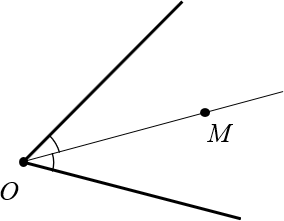
Докажем, что эта самая точка $M$ находится на одинаковом расстоянии от сторон угла.

Доказательство. Проведём из точки $M$ перпендикуляры к сторонам угла. Назовём их $M{{H}_{1}}$ и $M{{H}_{2}}$:

Провели перпендикуляры к сторонам угла

Получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. У них общая гипотенуза $OM$ и равные углы:

1. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$ по условию (поскольку $OM$ — биссектриса);
2. $angle M{{H}_{1}}O=angle M{{H}_{2}}O=90{}^circ $ по построению;
3. $angle OM{{H}_{1}}=angle OM{{H}_{2}}=90{}^circ -angle MO{{H}_{1}}$, поскольку сумма острых углов прямоугольного треугольника всегда равна 90 градусов.

Следовательно, треугольники равны по стороне и двум прилежащим углам (см. признаки равенства треугольников). Поэтому, в частности, $M{{H}_{2}}=M{{H}_{1}}$, т.е. расстояния от точки $O$ до сторон угла действительно равны. Что и требовалось доказать.:)

2. Если расстояния равны, то точка лежит на биссектрисе

Теперь обратная ситуация. Пусть дан угол $O$ и точка $M$, равноудалённая от сторон этого угла:

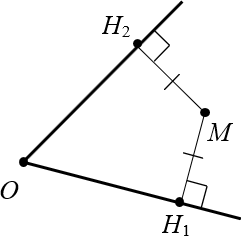
Докажем, что луч $OM$ — биссектриса, т.е. $angle MO{{H}_{1}}=angle MO{{H}_{2}}$.

Доказательство. Для начала проведём этот самый луч $OM$, иначе доказывать будет нечего:

Провели луч $OM$ внутри угла

Снова получили два прямоугольных треугольника: $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$. Очевидно, что они равны, поскольку:

1. Гипотенуза $OM$ — общая;
2. Катеты $M{{H}_{1}}=M{{H}_{2}}$ по условию (ведь точка $M$ равноудалена от сторон угла);
3. Оставшиеся катеты тоже равны, т.к. по теореме Пифагора $OH_{1}^{2}=OH_{2}^{2}=O{{M}^{2}}-MH_{1}^{2}$.

Следовательно, треугольники $vartriangle OM{{H}_{1}}$ и $vartriangle OM{{H}_{2}}$ по трём сторонам. В частности, равны их углы: $angle MO{{H}_{1}}=angle MO{{H}_{2}}$. А это как раз и означает, что $OM$ — биссектриса.

В заключение доказательства отметим красными дугами образовавшиеся равные углы:

Биссектриса разбила угол $angle {{H}_{1}}O{{H}_{2}}$ на два равных

Как видите, ничего сложного. Мы доказали, что биссектриса угла — это геометрическое место точек, равноудалённых до сторон этого угла.:)

Теперь, когда мы более-менее определились с терминологией, пора переходить на новый уровень. В следующем уроке мы разберём более сложные свойства биссектрисы и научимся применять их для решения настоящих задач.

Смотрите также:

1. Высота в треугольнике
2. Основное свойство биссектрисы угла в треугольнике и его применение для решения задач
3. Тест к уроку «Площади многоугольников на координатной сетке» (легкий)
4. Правила вычисления производных
5. Сводный тест по задачам B15 (2 вариант)
6. Симметрия корней и оптимизация ответов в тригонометрии

Слайд 1

5 класс МОУ-НОВОЩАПОВСКАЯ СОШ ЛАЗАРЕВА И.С. математика математика

Слайд 2

Начинается урок, Приготовься-ка дружок!

Слайд 3

Тема урока: Свойство биссектрисы угла.

Слайд 4

Девиз урока: Ни тридцать лет, ни тридцать столетий Не оказывают никакого влияния на ясность И красоту геометрических истин. Льюис Кэрролл.

Слайд 5

Цель урока : – способствовать формированию умений выявить свойство биссектрисы угла.

Слайд 6

Задачи урока : Образовательные – содействовать осознанному пониманию свойства биссектрисы угла. Развивающие – развивать умение говорить, составлять и задавать себе и другим вопросы; анализировать, делать выводы. Воспитательные – формирование положительной «Я концепции»: – через ситуацию успеха «Я способен» (способности); – в групповой работе «Я нужен», «Я управляю»; – при решении учебной задачи «Я могу», «Я владею» (воля, характер); – при моделировании «Я творю»; Ценностные ориентации – устойчивый учебно-познавательный интерес. Социальные установки – морально-этические принципы в работе в группах.

Слайд 7

ПРАВИЛА: С лушать. С лышать друг друга. Д ополнять. И справлять, помогать.

Слайд 8

Актуализация Расстояние между двумя точками. Длина отрезка соединяющего эти точки; Расстояние от точки до прямой. Длина перпендикуляра опущенного от данной точки на эту прямую; Какое свойство точек серединного перпендикуляра к отрезку вы знаете? Все точки серединного перпендикуляра равноудалены от концов отрезка.

Слайд 9

Что такое биссектриса? – Биссектриса (от лат. bi- «двойное», и sectio «разрезание») угла — луч с началом в вершине угла, делящий угол на две равные части. – Биссектриса угла (вместе с её продолжением) есть геометрическое место точек, равноудалённых от сторон угла (или их продолжений). Толковый словарь русского язык под ред. Д. Н. Ушакова .

Слайд 10

Как можно построить биссектрису? – с помощью транспортира; – с помощью линейки и циркуля; – перегибанием листа бумаги.

Слайд 11

Устная работа Расшифруйте слово и вы узнаете ключевое слово сегодняшнего урока. С 1) 72-17*4 = В 4)1/8:7 = О 3) 1/8*7 = Й 5)6/17*2 = Т 2) 36:2 – 48:3 = «Сосчитай, не зевай». 4 4 с с 1/56 1/56 в в 7/8 7/8 о о 12/17 й 2 т

Слайд 12

Маша и Саша решили путешествовать автостопом. В один из дней своего путешествия они оказались в треугольнике, образованным тремя дорогами, и тут у них разгорелся спор – в какую сторону и по какой дороге ехать. В конце концов они решили поехать по той дороге, по которой пойдет первая же машина. Покажите, где они должны стоять, чтобы находиться на одинаковом расстоянии от каждой из трех дорог. Ответ обоснуйте.

Слайд 13

Учебное исследование №1 1. Начертите тупой(прямой, острый)угол. 2. Проведите его биссектрису. 3. Отметьте на ней произвольную точку О. 4. Опустите из неё перпендикуляр на стороны угла. 5. Измерьте длины перпендикуляров и сравните их. 6. Будут ли точки этой биссектрисы равноудалены от сторон угла?

Слайд 14

контрпример Точки, не лежащие на биссектрисе, не обладают этим свойством, т.е не равноудалены от сторон угла А Р

Слайд 15

ВЫВОД: точки биссектрисы любого угла равноудалены от сторон угла. Это и есть свойство биссектрисы угла.

Слайд 16

Учебное исследование №2. Где же должны стоять ребята? Точка пересечения биссектрис – это и есть место, где должны стоять ребята, чтобы находиться на одинаковом расстоянии от каждой трёх дорог. Почему?

Слайд 17

Место, где ребята должны находиться

Слайд 18

Отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны, называется биссектрисой треугольника. б и с с е к т р и с а о Это одна из замечательных точек треугольника – точка пересечения биссектрис является центром вписанной окружности.

Слайд 19

Итог урока: Какую задачу мы решали сегодня на уроке? Каким свойством обладает биссектриса? Все точки биссектрисы любого угла равноудалены от его сторон.

Слайд 20

Самостоятельная работа Вариант1 Вариант 2 1. Начертите угол АВС =60 2. Проведите биссектрису. 3. Отложите на ней отрезок ВД= 4см. 4. Определите расстояние от точки Д до сторон угла. 5. Вывод. 1. Начертите угол АВС =80 2. Проведите биссектрису. 3. Отложите на ней отрезок ВД= 4см. 4. Определите расстояние от точки Д до сторон угла. 5.Вывод.

Слайд 21

Начертите разные по виду треугольники и проверьте в них свойство биссектрисы угла или С -37.3. в двух вариантах (раздать карточки). Домашнее задание

Слайд 22

« Дети имеют настоящее понимание только о тех вещах, которые они открыли сами , и каждый раз, когда мы стараемся учить чему-то быстро, мы удерживаем их от открытия вещей заново» (Ж. Пиаже)

Слайд 23

МОЛОДЦЫ!