Каким свойством обладают структурные группы механизма
Строение механизмов
Основной принцип образования механизмов с одноподвижными кинематическими парами был впервые сформулирован русским ученым Л.В. Ассуром (1914 г.). Он заключается в том, что любой механизм может быть образован путем последовательного присоединения к начальному (ведущему) звену (или ведущим звеньям) и стойке кинематических цепей (структурных групп) с нулевой степенью свободы. Это принцип носит методологический характер, так как позволяет:
- 1) объяснить строение сложных механизмов;
- 2) выбрать рациональный алгоритм (порядок) исследования механизма.
Последнее положение особенно важно при выполнении кинематического и кинетостатического исследований.
Группа звеньев, состоящая из стойки и подвижных звеньев, движение которых задано, называется начальным механизмом (НМ). Число подвижных звеньев в начальном механизме определяется числом степеней свободы механизма — числом входных (ведущих) звеньев, движение которых задано. Например, в механизме на рис. 3.1 при
начальный механизм состоит из кривошипа / (его движение задано) и стойки 6 (рис. 3.2, а). Его число степеней свободы соответственно равно значению
т.е. число степеней свободы начального механизма всегда равно числу степеней свободы исследуемого механизма. При W> 1 начальный механизм образуют те подвижные звенья, движения которых заданы (рис. 3.2, б).
Группа подвижных звеньев, связанных между собой одноподвижными кинематическими парами и при присоединении к механизму не изменяющих его числа степеней свободы, называются структурной группой. Условие существования структурной группы:
Рис. 3.1. Плоский рычажный механизм
Рис. 3.2. Виды начальных механизмов
где Д W — число степеней свободы структурной группы; п’, Р[ — число звеньев и число одноподвижных кинематических пар в структурной группе соответственно.
В уравнении (3.1) п’ и Р — всегда целые числа. Решим это уравнение относительно п’ или Р[:
Из выражений (3.2) и (3.3) следует, что число звеньев в структурной группе всегда является четным числом, а число одноподвижных кинематических пар — кратно трем (рис. 3.3). Здесь п = 4, Рх = 6. Число степеней свободы структурной группы:
Рис. 3.3. Иллюстрация кратности трем одноподвижных кинематических пар в структурной группе
При составлении схемы структурной группы предполагают, что звенья 1, 2, 3 образуют одноподвижные кинематические пары Л, В, С с разными звеньями механизма, к которому данная структурная группа присоединяется. Структурные группы различаются между собой количеством поводков, с помощью которых они присоединяются к механизму.
Поводок структурной группы — звено, образующее одноподвижную кинематическую пару с одним из звеньев механизма. Наиболее известны и употребительны двух- (рис. 3.4, а), трех- (рис. 3.4, б) и четырехповодковые (рис. 3.4, в) структурные группы. При сокращении названий структурных групп используются термины: 2ПГ — двухповодковая группа, ЗПГ — трехповодковая группа, 4ПГ — четырехповодковая группа и т.д. В механизмах технологических машин самыми употребительными структурными группами являются двухповодковые. Их существует пять видов, различающихся между собой
Рис. 3.4. Виды структурных групп по подвижностям сочетанием и взаимным расположением вращательных и поступательных кинематических пар. Структурные схемы всех видов двухповодковых групп с примерами приведены в табл. 3.1.
При структурном анализе механизма решается задача по его расслоению на отдельные структурные группы и определению в них
Таблица 3.1
Виды двухповодковых групп
Вид двухповодковой группы | Схема структурной группы | Характерные точки в структурной группе | Схема механизма в данной группе |
1 |  |  | |
2 |  |  |  |
3 |  |  |  |
4 |  |  |  |
5 |  |  |  |
характерных точек, движение которых подлежит изучению при исследовании механизма. Наслоение структурных групп в механизме может быть последовательным, параллельным или смешанным. Так, механизм на рис. 3.1 может быть разделен на группы, представленные на рис. 3.5. Он состоит из начального механизма (НМ) (рис. 3.5, а) двухповодковой группы первого вида (рис. 3.5, б) и двухповодковой группы второго вида (рис. 3.5, в).
Рис. 3.5. Начальный механизм и двухповодковые группы второго вида
Для такого механизма можно составить следующую структурную формулу:
где 6, 1; 2, 3;… — набор цифр, состоящий из номеров звеньев, которые образуют соответствующую структурную группу; —? — символ, указывающий порядок наслоения структурных групп. Причем число входящих стрелок соответствует числу поводков данной группы. Каждая стрелка направляется от той структурной группы, к которой присоединяется поводок очередной группы, изображенный этой стрелкой.
В общем виде структурная формула механизма при последовательном наслоении структурных групп имеет вид:
• при параллельном наслоении (рис. 3.6, а):
• при смешанном наслоении (рис. 3.6, б):
Так, например, структурная формула механизма на рис. 3.6, а имеет вид:
на рис. 3.6, б:
Рис. 3.6. Параллельное (а) и смешанное (б) наслоение структурных групп
При структурном синтезе проектируемые схемы новых механизмов находятся наслоением к начальному механизму структурных групп, а не отдельных звеньев. Вид и структура присоединяемых структурных групп определяются требуемым законом движения ведомого (выходного) звена.
Рассмотрим свойства структурных групп.
- 1. Присоединение или отбрасывание структурной группы не изменяет числа степеней свободы механизма. Это свойство связано с определением структурной группы, для которой характерно ДИ/= 0.
- 2. Структурная группа является статически определимой системой. Физический смысл второго свойства заключается в том, что для каждой структурной группы можно составить число уравнений, соответствующее числу неизвестных реакций, тем самым имеется возможность их нахождения. Связи, накладываемые одноподвижными кинематическими парами (две связи), являются неизвестными реакциями. Следовательно, число одноподвижных кинематических пар в структурной группе — Р[, а число неизвестных реакций — 2Р[. Для любого отдельного звена в плоскости можно составить три уравнения (ZFX = 0; Е/т = 0; ЪМ = 0). В структурной группе п’ подвижных звеньев. Тогда для структурной группы можно составить Ъп’ независимых уравнения. Из условия существования структурной группы (A1V= 0) следует:
т.е. она является статически определимой системой.
Принципы наслоения структурных групп в плоских механизмах могут быть обобщены и распространены на пространственные механизмы с низшими кинематическими парами (/>,, Р2, Р3), так как их структуры подчиняются одним и тем же законам. На основе аналогии условие существования пространственных структурных групп имеет вид:
или в механизме без общих связей:
а в механизме с общими связями (см. (2.10)):
где п’, Р’ — число звеньев, кинематических пар /-й подвижности в структурной группе соответственно.
Из выражений (3.7) и (3.8) следует, что пространственные структурные группы могут быть образованы любыми кинематическими парами с подвижностью от 1 до 3 при соответствующем числе звеньев (п’). Учитывая, что /-подвижную кинематическую пару можно заменить соответствующими /-одноподвижными кинематическими парами (кинематическим соединением) (рис. 3.7) при условии соблюдения закона движения механизма, то выражение (3.7) примет вид:
в котором п’и Р[ — целые числа. Определим их:
т.е. в пространственных структурных группах с одноподвижными кинематическими парами число звеньев кратно 5 (п’ = 5, 10, 15), а число Р[ пар кратно 6 {Р{ = 6, 12, 18,…).
Рис. 3.7. Кинематические пары
Пространственные структурные группы по аналогии с плоскими могут быть двухповодковыми (и’ = 5, Р[ = 6 ) (рис. 3.8, а), трехповодковыми («’ = 10, Р[ = 12) (рис. 3.8, б) и т.д.
Рис. 3.8. Преобразованные пространственные структурные группы
В пространственных структурных группах в отличие от плоских структурных групп используются соединительные звенья. Число этих звеньев зависит от вида кинематических пар. Любое соединительное звено с двумя одноподвижными кинематическими парами можно заменить одной двухподвижной кинематической парой, а два соединительных звена с тремя одноподвижными кинематическими парами — одной трехподвижной кинематической парой. Заменяя одноподвижные кинематические пары многоподвижными кинематическими парами, можно получить многообразие пространственных структурных групп, которые используются в современных механизмах.
Так, например, на рис. 3.9 представлена схема шасси самолета, на которой звенья 2, 3 образуют пространственную двухповодковую
Рис. 3.9. Схема шасси самолета
структурную группу. Нетрудно заметить, что если в этой группе наложить три общие связи, т.е. сделать механизм плоским, то эта структурная группа превратится в плоскую двухповодковую группу первого вида. Это обстоятельство указывает на взаимосвязь плоских и пространственных структурных групп.
В общем виде пространственная трехповодковая структурная группа (см. рис. 3.8, б) может быть преобразована в группу третьего вида, представленную на рис. 3.10, для которой выполняется условие ее существования:
Рис. 3.10. Структурная группа третьего вида
Естественно, данная структурная группа будет иметь другие схемы, если в ней использовать как одно-, так и двух- и трехподвижные плоские механизмы как с низшими, так и с высшими кинематическими парами, если в них эти пары будут заменены соответствующим образом низшими кинематическими парами (Р{, Р2, Р3) (рис. 3.11). Здесь двухподвижная пара А заменена поступательной парой А и вращательной парой С, на оси которой расположен центр кривизны конструктивного профиля кулачка в данном положении механизма. Длины звеньев ОС и СА зависят от положения точки контакта А и являются переменными величинами. Другими словами, для любого конкретного положения механизма будет соответствующая кинема-
Рис. 3.11. Преобразование кулачкового механизма в плоский рычажный механизм
тическая схема, хотя структурная схема для всех положений этого механизма будет одна и та же.
Источник
Условие существования любой структурной группы описывается формулой
W = 3n – 2P5 = 0.
Так как количество звеньев n и количество кинематических пар P5 – целые числа, то
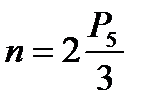– кратно 2, то есть чётно,
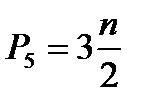– кратно 3.
Все структурные группы принято разделять на классы – со 2-го по 4-й.
Примеры структурных групп и начального механизма приведены на рис. 1.3.
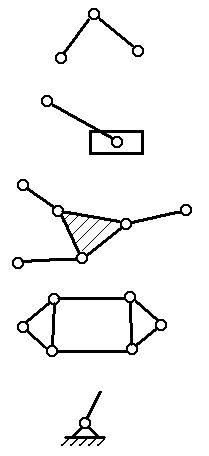Двухповодковая структурная группа 2-го кл.
Структурная группа 2-го кл.
Структурная группа 3-го кл.
Структурная группа 4-го кл.
Механизм 1-го кл. (начальный механизм)
Рис. 1.3. Примеры структурных групп
При добавлении к механизму 1-го класса различных структурных групп можно получить механизм, состоящий из одной или нескольких структурных групп и механизма 1-го класса.
Не путать класс механизма, класс структурной группы
и класс кинематической пары!
Механизмам присваивается определённый класс, соответствующий наивысшему классу входящих в него структурных групп. Примеры механизмов различных классов приведены на рис. 1.4.
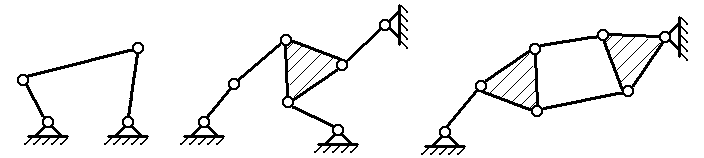
2-й кл. 3-й кл.4-й кл.
Рис. 1.4. Механизмы различных классов
Порядок структурной группы равен числу свободных кинематических пар, которыми группа присоединяется к более простому механизму. Свободные пары показаны стрелками (рис. 1.5).
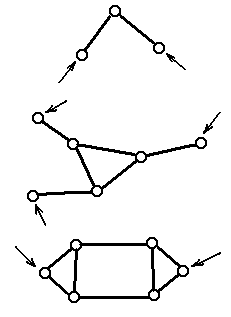
Структурная группа 2-го кл., 2-го порядка
(все структурные группы 2-го кл. имеют 2-й порядок)
Структурная группа 3-го кл., 3-го порядка
Структурная группа 4-го кл., 2-го порядка
Рис. 1.5. Примеры структурных групп различных классов
Наиболее распространённые структурные группы 2-го класса подразделяются на 5 видов (модификаций) (табл.)
Примечание. 1 – ведущее звено; 2 и 3 – звенья, образующие структурную группу.
Для определения класса механизма его расчленяют на структурные группы, начиная с конца механизма. За начало механизма принимают ведущее звено (начальный механизм).
От конца механизма отделяются поочерёдно простейшие структурные группы до тех пор, пока не останется лишь механизм 1-го класса (начальный механизм, их может быть несколько).
По классу структурных групп определяют класс механизма. Количество начальных механизмов равно величине W.
Пример расчленения плоского рычажного механизма на структурные группы показан на рис. 1.6. Предварительно вычисляют степень подвижности механизма W по формуле
W = 3n – 2P5 – P4.
В данном случае W = 1, а это значит, что в механизме должны быть одно ведущее звено и соответственно один начальный механизм.
а б в г
Рис. 1.6. Расчленение механизма на структурные группы:
а – исходный механизм; б – начальный механизм;
в – 2-й класс, 1-й вид; г – 2-й класс, 2-й вид
Избыточные связи
В некоторых случаях при проектировании механизмов для повышения жёсткости конструкции, улучшения условий передачи сил вводятся так называемые избыточные (пассивные) связи (дополнительные звенья), (рис. 1.7.).
Избыточная (пассивная) связь
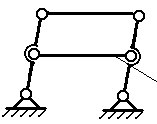
Рис. 1.7. Механизм с избыточной связью
В этом случае степень свободы вычисляется по формуле
W = 3n – 2P5 + q= 3×4 – 2×6 + 1 = 1,
где q – число избыточных (пассивных) связей.
Источник
В современном машиностроении все многообразие механизмов разбито на различные классы и группы в зависимости от общих классификационных признаков.
Структурный анализ механизма всегда предшествует его кинематическому и силовому расчетам.
Механизмы одного и того же класса имеют общие методы расчетов.
Деление механизмов на классы производится по структурным особенностям групп, составляющих данные механизм.
Структурные группы. Класс, порядок, вид групп Ассура. Согласно Л.В.Ассуру любой механизм образуется последовательным присоединением к входному звену (со стойкой) кинематических цепей, степень подвижности которых равна нулю. Такие цепи называются структурными группами Ассура. Если степень подвижности W=0, то число звеньев и пар плоского механизма, входящих в группу, связаны соотношением
Это уравнение имеет множество решений, состоящих из четного числа звеньев и кинематических пар 5-го класса, количество которых кратно 3.
Группами Ассура будут являться только неделимые цепи, т.е. такие, которые без разрушения нельзя разделить на самостоятельные структурные группы.
Класс, порядок, вид структурных групп. Группы Ассура разделяются на классы, каждая структурная группа имеет порядок, а в одном из классов, втором, различают еще и виды групп.
Класс группы Ассура определяется наивысшим классом контура, входящего в ее состав (табл. 1)
Таблица1
Кинематическая цепь, состоящая из двух звеньев и трех кинематических пар (n=2; ), всегда является группой Ассура второго класса.
Порядок структурной группы определяется числом внешних, свободных кинематических пар, которыми она присоединяется к другим звеньям механизма. В табл. 1 внешние пары затушеваны, они и определяют порядок структурной группы. Кинематические пары, входящие в замкнутый контур, называются внутренними. У групп Ассура второго класса всегда 2-й порядок.
Группы Ассура 2-го класса разделяются на пять видов, зависящих от взаимного расположения в группе вращательных и поступательных кинематических пар.
Виды групп Ассура 2-го класса представлены на рис. 1.
Рис. 1. Виды групп Ассура 2-го класса
Класс группы Ассура выше второго определяется числом внутренних кинематических пар, образующих замкнутый контур (табл. 1, контуры 3 и 4). Ведущее звено вместе со стойкой и кинематической парой, соединяющей их, называется механизмом 1-го класса и указывается стрелкой, направленной по движению ведущего звена.
Рис.2. Вращающееся ведущее (а) и поступательно движущееся (б) звенья
На рис. 2а представлено вращающееся ведущее звено, а на рис.2б
поступательно движущееся. Конструктивные особенности звеньев, не оказывающие влияния на движение механизма, на схемах не учитываются.
Класс механизма определяется наивысшим классом структурной группы, входящей в этот механизм. При определении класса механизма необходимо указать, какие звенья являются ведущими, т. к. в зависимости от выбора ведущих звеньев класс механизма может измениться.
В структурные группы входят только цепи с низшими кинематическими парами. Если в механизме имеются цепи с высшими кинематическими парами, каждая высшая пара должна быть заменена, и только после этого заменяющий механизм разбивается на структурные группы Ассура.
2. Замена высшей пары в плоском механизме
Каждая высшая кинематическая пара эквивалентна одному звену, оканчивающемуся двумя низшими парами. Вид низших пар зависит от соприкасающихся поверхностей звеньев.
Правила замены. Необходимо найти радиусы кривизны соприкасающихся поверхностей, в центре кругов кривизны поставить условные шарниры и между ними добавочное звено (рис. За). Если одна из контактируемых поверхностей прямолинейна, движение будет поступательным, а заменяющая пара -ползуном (рис. 3б).
Рис.3. Замена высших пар низшими
3.Структурный анализ механизма
Структурным анализом механизма называют определение количества ведущих звеньев, групп Ассура, последовательность их присоединения к кинематической цепи и класс механизма.
Структурный анализ возможен, если соблюдаются следующие условия:
I)число ведущих звеньев равно числу степеней свободы механизма;
2) ведущее звено входит в кинематическую пару со стойкой;
3)все кинематические пары относятся к 5-му классу.
Структура любого плоского механизма наглядно представляется с помощью формулы его строения. Формула строения механизма состоит из условного обозначения класса, порядка и вида каждой структурной группы, и схематично показывает порядок присоединения структурных групп к ведущим звеньям.
Например, если формула строения механизма
то первая цифра 1 указывает на механизм 1-го класса, в скобках (0-стойка, 1 -ведущее звено), т. е. ведущее звено со стойкой. Затем к ведущему звену присоединяется группа 2-го класса, 2-го порядка, 4-го вида; в скобках указаны номера звеньев, ее образующие.
В группе Ассура 3-го класса, 3-го порядка в скобках указаны номера звеньев, ее образующие. Одно из них поставлено в числителе, и оно носит название базисного, потому что к нему присоединяются более чем два других звена (их номера перечислены в знаменателе: 5, 6, 7).
Класс данного механизма третий, т. к. наивысший класс группы, входящей в этот механизм, – три.
4. Порядок проведения структурного анализа
1. Подсчитывается степень подвижности механизма по формуле Чебышева, для чего нумеруются подвижные звенья и определяется количество кинематических пар. При наличии высших кинематических пар их надо заменить цепями с низшими кинематическими парами.
Если в механизме есть лишние степени подвижности, их не учитывают. Могут оказаться в механизме и пассивные связи, которые не оказывают влияния на работу механизма. Применяются они в механизмах для увеличения жесткости, для более правильного распределения нагрузок. Лишние степени свободы служат для увеличения к.п.д. механизма и уменьшения износа.
Производится отделение групп Ассура, начиная с наиболее удаленной от ведущего звена. Если возможно, отделяется группа наиболее низкого класса. Если такую группу выделить невозможно, отделяется группа более высокого класса. Разложение механизма на структурные группы ведется до тех пор, пока не останутся ведущее звено и стойка. При этом необходимо проверять замкнутость оставшейся кинематической цепи. Каждое звено и любая кинематическая пара должны входить только в одну из структурных групп.
Записывается формула строения механизма, начиная с ведущего звена (механизма 1-го класса) и далее в порядке присоединения групп Ассура.
Указывается класс механизма.
5.Примеры структурного анализа
Пример 1. Кулачково-коромысловый механизм
Ролик 3 кулачкового механизма (рис. 4 а), образуя с коромыслом 2 вращательную пару 5-го класса, создает в механизме лишнюю степень подвижности. Он свободно вращается на своей оси, не оказывая никакого влияния на характер движения механизма. Ролик поставлен из конструктивных соображений для замены трения скольжения трением качения. Поэтому ролик 3 можно условно жестко закрепить коромыслом со звеном 2 (рис. 4 б). Тогда число подвижных звеньев механизма n=2, количество вращательных пар 5-го класса , они находятся в точках и , в точке контакта коромысла с кулачком – высшая пара 4-го класса, .
Степень подвижности механизма
W=3*2*2*2 -1 = 1.
Ведущим звеном выбран кулачок 1.
Высшая пара должна быть заменена добавочным условным звеном k (длина которого равна сумме радиусов кривизны и соприкасающихся поверхностей 1 и 2) и двумя низшими парами А и В, расположенными в центрах кривизны (рис. 4в).
Рис.4 Пример структурного анализа механизма с лишней степенью подвижности и высшей кинематической парой
Мгновенно заменяющий механизм представлен на рис.4в.
Кинематическая цепь этого механизма состоит из структурной группы 2-го класса,2-го порядка и 1-го вида и ведущего звена . Формула его строения:
.
Заменяющий механизм относится к механизму 2-го класса.
Исходный кулачковый механизм также относится к механизму 2-го класса.
Пример 2. Механизм с изменяемым классом
Рис.5.Пример структурного анализа механизма с изменяемым классом
Степень подвижности исходного механизма при n=5 и (рис.5а) W=3*5-2*7=1 указывает на наличие в нем одного ведущего звена.
Допустим, что входным звеном выбрано звено 1 (рис.5б). Делается попытка отделить от механизма группу Ассура 2-го класса ((n =2, ); звенья 3 и 4). Тогда оставшаяся цепь звеньев 1, 2, 5 будет незамкнутой, что приводит к неопределенности движения звеньев 2 и 5. Тот же результат получается при отделении от механизма звеньев 4, 5.
Правильное решение дает выделение из механизма группы Ассура, состоящей из четырех звеньев 2, 3, 4, 5 и шести пар (рис. 5в). Это группа Ассура .4. После отделения остается входное звено 1 и стойка 0 (механизм 1-го класса). Формула строения механизма в данном случае:
1(0,4)- (2,3,4,5),
т.е. механизм 4-го класса.
Если в данном механизме выбрать за входное звено 4, то класс его изменяется (рис. 5г). Цепь его ведомых звеньев 1, 2, 3, 5 представляет собой трехповодковую группу Ассура 3-го класса 3-го порядка. Формула строения механизма в этом случае:
1(0,4)- (2,1,3,5),
т.е механизм 3-го класса.
Таким образом, замена ведущего (начального) звена привела к понижению класса механизма.
Источник