Каким свойством обладают противоположные грани параллелепипеда
Что такое параллелепипед?
Что за слово такое мудреное – «параллелепипед»?
Что за многогранник скрывается за этим словом?
Что-то должно быть связано с параллельностью, не правда ли?
Так и есть. Читай статью и ты все поймешь!
Параллелепипед – многоугольник, образованный пересечением трех пар параллельных плоскостей.
Если слишком сложно, просто посмотри на картинку.
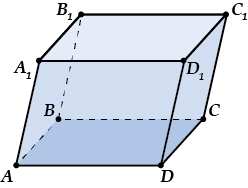
Какую фигуру из планиметрии (геометрии с «плоскими» фигурами) напоминает параллелепипед?
Немного похоже на параллелограмм, правда? Только «потолще» и слово подлиннее.

Смотри, запоминай и не путай!


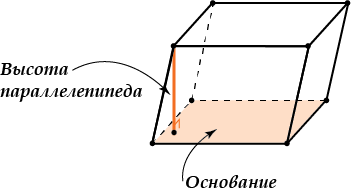

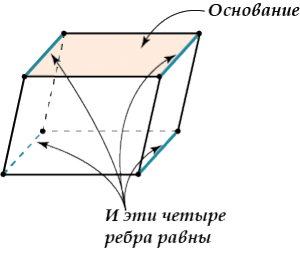
Высота – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Та грань, на которую опущена высота, называется основанием.
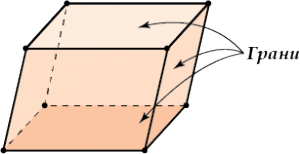
- Все грани параллелепипеда – параллелограммы.
- Противоположные грани параллелепипеда параллельны и равны.
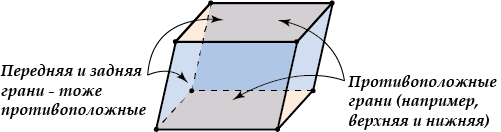
Внимание: передняя и задняя грани параллелепипеда равны, верхняя и нижняя – тоже равны, но не равны (не обязаны быть равны) передняя и верхняя грани – потому что они не противоположные, асмежные.
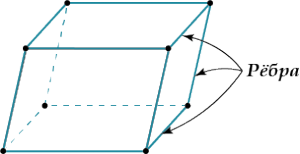
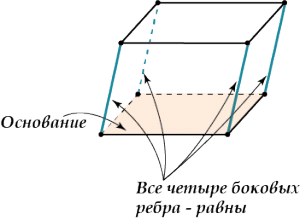
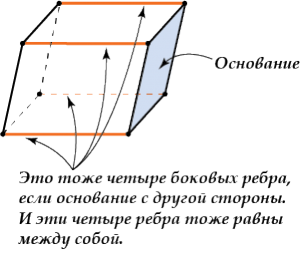
- Боковые ребра параллелепипеда равны.
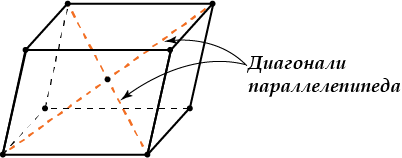
- Диагонали параллелепипеда пересекаются и точкой пересечения делятся пополам.
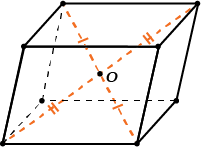
Точка пересечения диагоналей называется центром параллелепипеда.
Прямым называется параллелепипед, у которого боковые ребра перпендикулярны основанию.
Вот так:
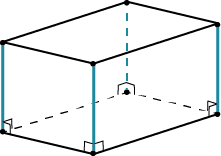
У прямого параллелепипеда в основании – параллелограмм, а боковые грани – прямоугольники.
Прямоугольным называется параллелепипед, у которого в основании прямоугольник, а боковые ребра перпендикулярны основанию.
Это такая обувная коробка:
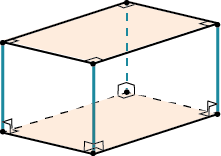
У прямоугольного параллелепипеда все грани – прямоугольники.
Давай-ка теперь выведем одну интересную формулу для диагонали прямоугольного параллелепипеда.

Диагональ прямоугольного параллелепипеда равна сумме квадратов его измерений.
( displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}).
Видишь, как красиво? На теорему Пифагора похоже, правда? И формула эта как раз и получается из теоремы Пифагора.
Смотри:
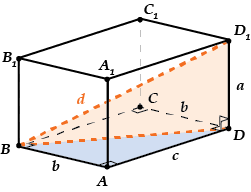
( displaystyle Delta BAD) – прямоугольный, поэтому
( displaystyle B{{D}^{2}}=A{{B}^{2}}+A{{D}^{2}}={{b}^{2}}+{{c}^{2}})
( displaystyle Delta BD{{D}_{1}}) – тоже прямоугольный!
Поэтому
( displaystyle B{{D}_{1}}^{2}=B{{D}^{2}}+D{{D}_{1}}^{2}),
Подставим:
( displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}})
Вывели формулу.
Куб – параллелепипед, у которого все грани квадраты.

Все ребра куба равны.
Кстати, заметь, что куб – частный вид прямоугольного параллелепипеда.
Поэтому для диагонали куба действует формула, которую мы получили для прямоугольного параллелепипеда.
( displaystyle {{d}^{2}}={{a}^{2}}+{{a}^{2}}+{{a}^{2}}),
То есть
( displaystyle d=asqrt{3})
Давай убедимся в пользе этой формулы.
Представь, что у тебя задача: «Диагональ куба равна ( displaystyle 5sqrt{3}). Найти полную поверхность».
Пользуясь нашей формулой: ( displaystyle d=asqrt{3}), мы узнали, что ( displaystyle 5sqrt{3}=asqrt{3} ), то есть ( displaystyle a=5).
Значит полная поверхность – шесть площадей квадратов со стороной ( displaystyle a) -равна:
( displaystyle S=6cdot {{a}^{2}}=6cdot 25=150).
Видишь, как быстро? И ты применяй!
Определения:

Параллелепипед — это четырехугольная призма (многогранник с ( displaystyle 6) гранями), все грани которой — параллелограммы.

Прямой параллелепипед — это параллелепипед, у которого ( displaystyle 4) боковые грани — прямоугольники.

Прямоугольный параллелепипед — параллелепипед, у которого все грани – прямоугольники

Куб — параллелепипед, у которого все грани квадраты.
Высота параллелепипеда – перпендикуляр, опущенный из любой вершины параллелепипеда на противоположную грань.
Свойства:
- Противолежащие грани параллелепипеда параллельны и равны.
- Диагонали параллелепипеда пересекаются в одной точке и делятся ею пополам.
- Любой отрезок с концами, принадлежащими поверхности параллелепипеда и проходящий через точку пересечения диагоналей (центр параллелепипеда), делится ею пополам.
- Все диагонали прямоугольного параллелепипеда равны между собой и равны сумме квадратов его измерений.
( displaystyle {{d}^{2}}={{a}^{2}}+{{b}^{2}}+{{c}^{2}}).

P.S. Последний бесценный совет ????
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
- проверить свою готовность к каждому типу задач на ЕГЭ (пройдя тест);
- подтянуть слабые места с помощью видеоуроков, вебинаров;
- понять тему с помощью статей учебника YouClever;
- набить руку, решая задачи и получая проверку и решения;
- сдать пробный ЕГЭ и получить сразу оценку и разбор ошибок.
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Время услышать тебя!
Теперь ты знаешь все про параллелепипед и куб. Ты воспользуешься этим в решении многих задач стереометрии!
Считай, ты помог себе из будущего ????
А теперь мы хотим услышать тебя. Напиши в комментариях ниже свое мнение об этой статье!
Помогла ли она тебе? Все ли было понятно?
А еще ты можешь задать любой вопрос. Мы ответим!
Успехов!
Источник
Тетраэдр. Виды тетраэдров
Тетраэдр (четырёхгранник) — многогранник, гранями которого являются четыре треугольника (от греческого tetra — четыре и hedra — грань).
Рис. 1
У тетраэдра (4) грани, (4) вершины и (6) рёбер (Рис. 1).
Один из треугольников называется основанием тетраэдра, а три остальные — боковыми гранями тетраэдра.
В зависимости от видов треугольников и их расположения выделяют разные виды тетраэдров.
В школьном курсе чаще говорят о следующих видах тетраэдра:
– равногранный тетраэдр, у которого все грани — равные между собой треугольники;
– правильная треугольная пирамида — основание — равносторонний треугольник, все боковые грани — одинаковые равнобедренные треугольники (Рис. 3);
– правильный тетраэдр, у которого все четыре грани — равносторонние треугольники (Рис. 2).
Рис. 2 Рис. 3
Свойство правильного тетраэдра:
из определения правильного многогранника следует, что все рёбра тетраэдра имеют равную длину, а грани — равную площадь.
Параллелепипед. Виды параллелепипедов
Параллелепипедом называется многогранник, у которого (6) граней — параллелограммы.
Рис. 4
У параллелепипеда, как отмечено, (6) граней, (8) вершин и (12) рёбер (Рис. 4).
Две грани параллелепипеда, имеющие общее ребро, называются смежными, а не имеющие общих рёбер — противоположными.
Обычно выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани — боковыми гранями параллелепипеда.
Рёбра параллелепипеда, не принадлежащие основаниям, называют боковыми рёбрами.
Отрезок, соединяющий две вершины, не принадлежащие одной грани, называется диагональю параллелепипеда (Рис. 5).
Рис. 5
В зависимости от видов параллелограммов и их расположения выделяют разные виды параллелепипедов:
параллелепипеды могут быть прямые и наклонные.
У прямых параллелепипедов боковые грани — прямоугольники (Рис. 5),
у наклонных — параллелограммы (Рис. 4).
Прямой параллелепипед, у которого основанием тоже является прямоугольник, называется прямоугольным параллелепипедом.
Рис. 6
Длины непараллельных рёбер прямоугольного параллелепипеда называются его линейными размерами (измерениями).
У прямоугольного параллелепипеда — три линейных размера: DA, DC, DD1 (Рис. 6).
Свойства параллелепипеда:
– противоположные грани параллелепипеда равны и параллельны.
– Все четыре диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
– Боковые грани прямого параллелепипеда — прямоугольники.
Построение сечения тетраэдра и параллелепипеда
Плоскостью сечения многогранника можно назвать любую плоскость, по обе стороны которой находятся точки многогранника.
Секущая плоскость пересекает грани многогранников по отрезкам.
Многоугольник, сторонами которого являются эти отрезки, называется сечением многогранника.
Так как у тетраэдра (4) грани, то сечением тетраэдра может быть треугольник (Рис. 7) или
четырёхугольник (Рис. 8).
Рис. 7 Рис. 8
У параллелепипеда (6) граней, поэтому сечением этого многогранника может быть треугольник (Рис. 9), четырёхугольник ( Рис. 10), пятиугольник (Рис. 11) или шестиугольник (Рис. 12).
При построении сечения надо вспомнить следующие знания из предыдущих тем:
1. если две точки прямой принадлежат плоскости, то прямая находится в этой плоскости.
2. Если две плоскости имеют общую точку, то эти плоскости пересекаются по прямой.
3. Если плоскость пересекает две параллельные плоскости, то линии пересечения параллельны.
Пример:
Задача
Построить сечение параллелепипеда плоскостью, которая проходит через точки (K), (M) и (N).
1. Проводим (MK), так как обе точки находятся в одной плоскости;
2. MK∩CC1=X — непараллельные прямые в одной плоскости пересекаются;
3. проводим (XN), так как обе точки находятся в одной плоскости;
4. XN∩D1C1=P;
5. проводим (MP), так как обе точки находятся в одной плоскости;
6. через точку (N) в плоскости основания NL∥MP, так как линии пересечения параллельных плоскостей с третьей плоскостью должны быть параллельны;
7. соединяем (N) и (L) и получаем сечение (MPNLK).
Источник
Поверхность, составленная из двух равных параллелограммов АВСD и А1В1С1D1 и четырех параллелограммов АВВ1А1, ВСС1В1, СDD1С1, DАА1D1, называется параллелепипедом (рис. 1).
Рис. 1
То есть: имеем два равных параллелограмма АВСD и А1В1С1D1 (основания), они лежат в параллельных плоскостях так, что боковые ребра АА1, ВВ1, DD1, СС1 параллельны. Таким образом, составленная из параллелограммов поверхность называется параллелепипедом.
Свойства параллелепипеда.
1. Противоположные грани параллелепипеда параллельны и равны.
(фигуры равны, то есть их можно совместить наложением)
Например:
АВСD = А1В1С1D1 (равные параллелограммы по определению),
АА1В1В = DD1С1С (так как АА1В1В и DD1С1С – противоположные грани параллелепипеда),
АА1D1D = ВВ1С1С (так как АА1D1D и ВВ1С1С – противоположные грани параллелепипеда).
2. Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам.
Диагонали АС1, В1D, А1С, D1В пересекаются в одной точке О, и каждая диагональ делится этой точкой пополам (рис. 2).
Рис. 2
3. Имеются три четверки равных и параллельных ребер: 1 – АВ, А1В1, D1C1, DC, 2 – AD, A1D1, B1C1, BC, 3 – АА1, ВВ1, СС1, DD1.
Определение. Параллелепипед называется прямым, если его боковые ребра перпендикулярны основаниям.
Пусть боковое ребро АА1 перпендикулярно основанию (рис. 3). Это означает, что прямая АА1 перпендикулярна прямым АD и АВ, которые лежат в плоскости основания. А, значит, в боковых гранях лежат прямоугольники. А в основаниях лежат произвольные параллелограммы. Обозначим, ∠BAD = φ, угол φ может быть любым.
Рис. 3
Определение. Параллелепипед называется прямоугольным, если его боковые ребра перпендикулярны к основанию. Основания являются прямоугольниками.
Параллелепипед АВСDА1В1С1D1 – прямоугольный (рис. 4), если:
1. АА1⊥ АВСD (боковое ребро перпендикулярно плоскости основания, то есть параллелепипед прямой).
2. ∠ВАD = 90°, т. е. в основании лежит прямоугольник.
Рис. 4
Прямоугольный параллелепипед обладает всеми свойствами произвольного параллелепипеда. Но есть дополнительные свойства, которые выводятся из определения прямоугольного параллелепипеда.
1. В прямоугольном параллелепипеде все шесть граней прямоугольники.
АВСD и А1В1С1D1 – прямоугольники по определению.
2. Боковые ребра перпендикулярны основанию. Значит, все боковые грани прямоугольники.
3. Все двугранные углы прямоугольного параллелепипеда прямые.
Рассмотрим, например, двугранный угол с ребром АВ, т. е. двугранный угол между плоскостями АВВ1 и АВС.
АВ – ребро, точка А1 лежит в одной плоскости – в плоскости АВВ1, а точка D в другой – в плоскости А1В1С1D1. Тогда рассматриваемый двугранный угол можно еще обозначить следующим образом: ∠А1АВD.
Возьмем точку А на ребре АВ. АА1 – перпендикуляр к ребру АВ в плоскости АВВ1, AD перпендикуляр к ребру АВ в плоскости АВС. Значит, ∠А1АD – линейный угол данного двугранного угла. ∠А1АD = 90°, значит, двугранный угол при ребре АВ равен 90°.
∠(АВВ1, АВС) = ∠(АВ) = ∠А1АВD= ∠А1АD = 90°.
Аналогично доказывается, что любые двугранные углы прямоугольного параллелепипеда прямые.
Теорема. Квадрат диагонали прямоугольного параллелепипеда равен сумме квадратов трех его измерений.
Примечание. Длины трех ребер, исходящих из одной вершины, являются измерениями прямоугольного параллелепипеда. Их иногда называют длина, ширина, высота.
Дано: АВСDА1В1С1D1 – прямоугольный параллелепипед (рис. 5).
Доказать: .
Рис. 5
Доказательство:
Прямая СС1 перпендикулярна плоскости АВС, а значит, и прямой АС. Значит, треугольник СС1А – прямоугольный. По теореме Пифагора:
Рассмотрим прямоугольный треугольник АВС. По теореме Пифагора:
Но ВС и AD – противоположные стороны прямоугольника. Значит, ВС = AD. Тогда:
Так как , а , то. Поскольку СС1 = АА1, то что и требовалось доказать.
Следствие: Диагонали прямоугольного параллелепипеда равны.
Обозначим измерения параллелепипеда АВС как a, b, c (см. рис. 6), тогда АС1 = СА1 = В1D = DВ1 =
Рис. 6
Источник
Тема урока:«Параллелепипед и его свойства». 10 класс.
Учитель математики МБОУ СОШ р.п. Евлашево Кузнецкого района Кузьмина Л.М.
Цель урока: создать условия для формирования представления учащихся о параллелепипеде, его видах и свойствах.
Задачи урока:
образовательная: формирование понятия параллелепипеда и ознакомление учащихся с его элементами и свойствами; решение задач на применение свойств параллелепипеда;
развивающая: развитие логического мышления, памяти, внимания, умения планировать свою работу, ориентироваться в нестандартной ситуации;
воспитательная: воспитание нравственных качеств личности, ответственности, самостоятельности, формирование интереса к изучению математики.
Тип урока: урок усвоения новых знаний (нестандартный).
Форма проведения: урок – исследование.
Методы обучения: индуктивно-репродуктивный, дедуктивно-эвристический.
Требования к ЗУН:
Учащиеся должны знать:
определение параллелепипеда;
элементы и свойства параллелепипеда.
Учащиеся должны уметь:
– доказывать свойства параллелепипеда и применять их при решении задач.
План урока:
Организационный момент (3 мин)
Вводная часть (5мин)
Основная часть(34 мин)
Заключительная часть (3 мин)
Ход урока.
1. Организационный момент включает в себя приветствие учителем класса, проверку отсутствующих, готовность помещения к уроку.
Здравствуйте ребята. Садитесь. У кого вопросы по домашнему заданию?
О математике существует много высказываний, но мне близко по духу вот это. «Математика существует не для того, чтобы навязывать кому-то тяжёлую работу. Наоборот, она существует только для удовольствия. Для удовольствия тех, кто может анализировать то, что он делает или может сделать, или то что уже сделал в надежде сделать ещё лучше».
А вы получаете удовольствие от уроков математики? Когда? Тогда все должны сегодня постараться, чтобы этот урок принёс удовольствие от сделанного и мне и вам.
Внимание на слайд. Разбейте на группы данные фигуры.
По какому признаку вы это сделали? (фигуры-тела, треугольники-параллелограммы, параллелепипеды –тетраэдры, изученные-неизученные))
Попробуйте определить тему урока.
Поставьте цель перед собой. Чему-бы вы хотели научиться?
2. Вводная часть.
Как вы думаете какие знания являются фундаментом нашего урока? (признаки параллелограмма и свойства параллельных плоскостей).
Давайте их повторим, но сформулируем вопрос с сомнением. Начнём со слов верно ли. Пожалуйста, кто начнёт? Верно ли, что параллелепипед в переводе с греческого рядом идущие плоскости? (да)
3. Основная часть.
Сложно было формулировать вопросы? Вы получили удовольствие от своей работы? Почему?
1. Параллелепипед и его элементы.
Учитель. Рассмотрим два равных параллелограмма ABCD и A1B1C1D1, расположенных в параллельных плоскостях так, что отрезки AA1, BB1, CC1 и DD1 параллельны. Четырехугольники ABB1A1, ВСС1В1,CDD1C1 и DAA1D1 также являются параллелограммами. Почему, объясните?
Учащиеся. Так как,в четырёхугольнике 2 противоположные стороны параллельны (по условию) и равны (по свойству)
Учитель. Поверхность, составленная из двух равных параллелограммов ABCD и A1B1C1D1 и четырех параллелограммов ABB1A1, ВСС1В1, CDD1C1 и DAA1D1, называется параллелепипедом и обозначается так ABCDA1B1C1D1
Параллелограммы, из которых составлен параллелепипед называются гранями.Часто выделяют какие-нибудь две противоположные грани и называют их основаниями, а остальные грани – боковыми гранями параллелепипеда.
Стороны гранейназываются ребрами параллелепипеда. Вершины параллелограммов называютсявершинами параллелепипеда.
Отрезок, соединяющий противоположные вершины, называется диагональю параллелепипеда.
Обратимся к первому слайду и попробуем проклассифицировать параллелепипеды. Можно ли их разбить на группы?
Да. Они бывают прямые и наклонные. Исследуем свойства различных параллелепипедов.
Работа в группах. Отметить какими свойствами обладает данный параллелепипед. (2мин). Далее ученик выходит к доске, прикрепляет листочек на доску и рассказывает.
Обобщим материал. Так какими свойствами обладают все параллелепипеды?
-все боковые рёбра равны;
– основания равны;
– диагонали пересекаются в одной точке, и делятся пополам
2. Свойства параллелепипеда.
Исследовав, рёбра попытаемся выяснить, как ведут себя грани. Работа в группах.
1гр выясняет, будут ли равны противоположные грани.
2гр. Выясняет, будут ли противоположные грани равны .
3 группа выясняет, делятся ли диагонали пополам.
4гр выясняет, все ли диагонали пересекаются в одной точке.
Свойство 1: Противоположные грани параллелепипеда параллельны и равны
Доказательство: 
Докажем, например, параллельность и равенство граней ABB1A1,DСС1D1.
Учитель. Докажем теперь равенство этих граней. Так как все грани параллелепипеда – параллелограммы, то АВ=DC и AA1=DD1. По этой же причине стороны углов A1AB и D1DC соответственно сонаправлены, и,значит, эти углы равны.
Из этого следует,Что две смежные стороны и угол между ними параллелограмма АВВ1А1 соответственно равны двум смежным сторонам и углу между ними параллелограмма DCС1D1, поэтому эти параллелограммы равны.
Свойство 2:Диагонали параллелепипеда пересекаются в одной точке и делятся этой точкой пополам. (запишем в листочки).
Доказательство: 
Чтобы доказать это свойство, рассмотрим четырехугольник A1D1CB, диагонали которого A1C и D1B являются диагоналями параллелепипеда ABCDA1B1C1D1
Поэтому диагонали A1C и D1B пересекаются в некоторой точке О и этой точкой, делятся пополам.
Далее рассмотрим четырехугольник AD1C1B(слайд 12).
Он также является параллелограммом и, следовательно,
его диагонали A1C и D1B пересекаются и точкой пересечения делятся пополам.
Учитель. Но серединой диагонали D1B является точка О. Таким образом, диагоналиA1C, D1B и АС1 пересекаются в точке О и делятся этой точкой пополам.
Наконец, рассматривая четырехугольник А1В1СD точно так же устанавливаем, что и четвертая диагональ параллелепипедаDB1проходит через точку О и делит ею пополам(слайд 13).
Итак, подведём итог. Что нового вы узнали на уроке? Было сложно? Основное условие: не запускать материал.
Решение задач.
Задача №77. Сумма всех ребер параллелепипеда ABCDA1B1C1D1 равна 120 см. Найдите каждое ребро параллелепипеда, если .
Запись на доске и в тетрадях:
Дано: ABCDA1B1C1D1 – параллелепипед,
АВ+ВС+СD+DA+A1B1+B1C1+C1D1+D1A1+AA1+BB1+CC1+DD1=120 см,
Найти: АВ, ВС, СD, DA, A1B1, B1C1, C1D1, D1A1,AA1, BB1, CC1, DD1
Решение:
Учитель. Обозначим одно из ребер через х. Выразим через х ребра АВ, ВС.
Ученик. Пусть ВВ1=х. Тогда ,
Запись на доске и в тетрадях:
Пусть ВВ1=х. Тогда ,
Из условия задачи
;
Ответ: 12, 8, 10 см.
Задача № 78. На рисунке изображен параллелепипед ABCDA1B1C1D1 , на ребрах которого отмечены точки M, N, M1 и N1 так, что АМ=CN=A1M1=C1N1. Докажите, что МВNDM1B1N1D1 – параллелепипед.
Дано: ABCDA1B1C1D1 – параллелепипед, МАВ, М1∊ А1В1, N∊DC, N1∊D1C1, АМ=CN=A1M1=C1N1.
Доказать, что МВNDM1B1N1D1 – параллелепипед.
Доказательство:
Учитель. Рассмотрим четырехугольник MBND. Докажем, что этот четырехугольник параллелограмм.
Ученик.ABCD – параллелограмм по условию, значит АВ=CD.
Учитель. Из чего следует равенство ВМ и DN?
Ученик. АВ – АМ = CD – CN, то есть ВМ=DN.
Ученик. По признаку параллелограмма, MBND – параллелограмм.
Ученик. Аналогично, N1B1M1D1 – параллелограмм.NDM=∠N1D1M1 как углы с соответственно параллельными и одинаково направленными сторонами.
Ученик. Параллелограммы MBND и M1B1N1D1равны, так как равны их соответствующие стороны и угол между ними.
Учитель. Докажем, сто А1М1МА, С1NN1C – параллелограммы.
Ученик. А1М1=АМ, поэтому А1М1МА – паралеллограмм.
Запись на доске и в тетрадях:
А1М1=АМ, поэтому А1М1МА – паралеллограмм, М1М‖А1А‖В1В.
Ученик. Аналогично, С1NN1C – параллелограмм. Отрезки параллельных прямых, заключенные между параллельными плоскостями, равны, поэтому ММ1=ВВ1=СС1=NN1=DD1.
Ученик. По признаку параллелограмма четырехугольники МВВ1М1, BNN1B1, DNN1D1 и MDD1M1 – параллелограммы. По определению МВNDM1B1N1D1 – параллелепипед.
4. Заключительная часть.
Вернёмся к началу урока. Помните какие задачи вы перед собой поставили? Удалось ли их решить? У вас на столах есть 2 стикера. Красный и зелёный. На красном укажите, где вы готовы изучать данный вопрос: только на уроке, во внеурочное время, заняться исследовательской деятельностью.
А зелёный – прикрепите на ось математического удовлетворения, оценив свою работу по пятибалльной системе.
Всем спасибо за урок.
Домашнее задание. П 13, Свойства. Задача на выбор, с учётом усвоения материала №76, 78*
Творческое задание изготовить модель любого параллелепипеда из спиц, бумаги, проволоки для использования их на дальнейших уроках.
«Параллелепипед и его свойства».
Параллелепипед и его элементы.


Поверхность, составленная из двух равных параллелограммов ABCD и A1B1C1D1 и четырех параллелограммов ABB1A1 ВСС1В1, CDD1C1 и DAA1D1, называется_____________________________________обозначается так __________________.
Параллелограммы, из которых составлен параллелепипед называются ________________. В параллелепипеде ABCDA1B1C1D1 гранями являются параллелограммы_________________________________________________________________________. Стороны граней называются ______________________________________________________. В параллелепипеде ABCDA1B1C1D1 отрезки __________________________________________
являются ребрами. Вершины параллелограммов называются _________________________ параллелепипеда. В параллелепипеде ABCDA1B1C1D1 точки __________________________________________являются вершинами.
Параллелепипед имеет граней, ребер и вершин. Две грани параллелепипеда, имеющие общее ребро, называются _____________________(например грани _______________и_________________), а не имеющие общих ребер –___________________________________(например _________и___________). Отрезок, соединяющий противоположные вершины, называется ________________________ параллелепипеда. Каждый параллелепипед имеет __________ диагонали._____________________________– диагонали параллелограмма ABCDA1B1C1D1.
Часто выделяют какие-нибудь две противоположные грани и называют их ____________________, а остальные грани – _________параллелепипеда.
ГР 1. Свойства параллелепипеда.
Свойство 1: Противоположные грани параллелепипеда параллельны.
Дано:ABCDA1B1C1D1-параллелепипед, 
Доказать: АA1B1B|| DСС1D1
Доказательство:
Так как ABCD и DAA1D1___________________,то АВ||DCиAA1||DD1. Таким образом, две пересекающиеся прямые АВ и AA1 одной грани соответственно двум пересекающимся прямым DC и DD1 другой грани. Отсюда попараллельности следует, что грани ABB1A1 и DСС1D1
ГР 2. Свойства параллелепипеда.
Свойство 1: Противоположные грани ?
