Каким свойством обладают накрест лежащие углы

Цели урока:

Образовательные

• повторить определение параллельных прямых,
  смежных и вертикальных углов;
• формировать понятие накрест лежащих,
  односторонних и соответственных углов;
• рассмотреть первый признак параллельности
  прямых и научить применять при решении задач;
• познакомится с новым способом доказательства
  теорем: способ от противного;

Воспитательные

• воспитывать познавательную потребность,
  интерес к предмету;
• воспитывать аккуратность построений
  геометрических рисунков; культуру речи и
  культуру общения;

Развивающие

• развивать внимание, наблюдательность, память,
  логическое мышление;
• развивать умение работать с компьютером и
  интерактивной доской.

Ход урока

I. Орг. момент.

Здравствуйте, ребята, и все гости нашего урока.
Слайд №2

– Этот урок я хочу начать словами:

“В науке нет широкой столбовой дороги. И только
тот достигнет ее сияющих вершин, кто не страшась
усталости карабкается по ее каменистым тропам”
(Карл Маркс).

– Так вот, ребята, изучая геометрию, мы и будем
карабкаться по ее каменистым тропам и очень
надеюсь, что ближайшие 40 минут пройдут с пользой
для всех.

II. Актуализация опорных знаний.

Прежде чем приступить к открытию новых знаний,
давайте повторим то, что нам для этого
понадобится.

– Что вы знаете о взаимном расположении двух
прямых на плоскости?

(Две прямые на плоскости могут пересекаться,
т.е. иметь одну общую точку или они не
пересекаются, т.е. не имеют общих точек)

Слайд № 3

– Рассмотрим рис.1. Как называются углы,
полученные при пересечении прямых? (подробные
вопросы про вертикальные и смежные углы)

– Рассмотрим рис.2. Что на нём изображено?

Две параллельные прямые
Не прикоснутся никогда
Друг к другу, как бы не хотели
Ни через год, ни через два.

Слайд №4

Слово параллельные произошло от греческого
слова “параллелос”, что в переводе на русский
язык означает “идущие рядом”.

– А теперь оглянемся вокруг, попробуем найти, ну
прямые вряд ли, параллельные отрезки. (Учащиеся
приводят примеры.)

Слайд №5

– Да действительно, параллельные прямые прочно
закрепились в нашей жизни.

Слайд №6

А вы когда-нибудь обращали внимание на
государственные флаги. Очень многие из них
представляют полотнище состоящие или содержащие
параллельные полосы – отрезки. Расположены
горизонтально и вертикально.

Слайд №7

Ребята, а вы никогда не задумывались, что было
бы в мире, если бы не было параллельных прямых,
отрезков?

(Не могли бы двигаться трамваи, поезда,
троллейбусы, машины сталкивались бы на дорогах,
рушились бы здания). Наверное, можно сказать, что
наступил бы всеобщий хаос.

Слайд №8

В начале XX века в живописи появилось новое
течение, которое называлось “кубизм”. Это
течение появилось как вызов стандартной
красивости салонного искусства.

Слайд №9

Ярким представителем данного направления был
художник Пабло Пикассо.

Слайд №10

Посмотрите на его картину “Мужская голова”.
Слайд с картинкой. Весь рисунок состоит из прямых
и пересекающихся линий. Создаётся впечатление,
что в голове этого человека множество
противоречивых мыслей, что весь он в сомнениях и
терзаниях.

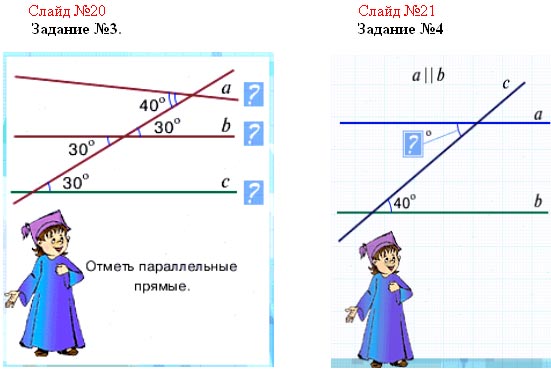
Просим назвать параллельные прямые

Слайд №11

Показ слайдов с оптические иллюзии

Ребята, можем ли мы, основываясь на нашем зрении
утверждать, что прямые параллельны или не
параллельны?

Ребята: Нет.

Учитель: Как же нам быть в таких
ситуациях?

В этих случаях помогают нам доказать
параллельность или не параллельность прямых
признаки.

– Ребята, возьмите опорные конспекты и в них
запишите число, классная работа и тему урока.

Слайд № 12

– Ой, ребята посмотрите компьютерные вирусы
уничтожили некоторые буквы в слове. Помогите мне,
какие буквы мы должны сюда написать!

III. Сообщение темы и целей урока.

Слайд №13

Так вот, ребята сегодня на уроке мы узнаем, как
называются углы, образованные при пересечении
двух прямых третьей, уметь их находить на
рисунке, докажем признаки параллельности прямых
и научимся применять их на практике.

IV. Объяснение нового материала.

(на уроке применяется опорный конспект (приложение), раздаётся каждому
ученику на перемене)

Прежде чем изучать признаки, мы должны
познакомиться с углами, которые образуются при
пересечении двух прямых третьей прямой.

Слайд №14

Начертите в тетради две прямые a и b и прямую с,
которая пересекает прямые a и b. Прямая с
называется секущей. При этом образовалось
несколько пар углов, часть из которых вам уже
знакома.

Названия каких углов вы уже знаете?
Вертикальные углы.

Назовите, какие углы являются вертикальными.
1 и 3, 2 и 4, 5 и 7, 6 и 8

Каким свойством обладают вертикальные углы?
Они равны.
Какие ещё пары углов вы знаете?
Смежные.

Назовите их?
1 и 2, 2 и 3, 1 и 4, 4 и 3

Достаточно. Каким свойством обладают смежные
углы?
Их сумма равна 180° .

Но на рисунке есть ещё пары неразвернутых
углов, которые пока вы не знаете.

Запишите:

Слайд №15

Потренируемся на другом рисунке находить эти
пары углов.

V. Физкультминутка.

Подняли обе руки параллельно вверх.
Вытянули обе руки параллельно вперёд.
Образовали руками развернутый угол.
Сколько градусов в развернутом угле? 180°.
Левую руку подняли вверх. Какой получился угол?
90°
Как расположены руки? Перпендикулярно.
Обе руки опустили вниз. Как они расположены?
Параллельно.

Хорошо, продолжаем наш урок.

VI. Изучение признаков параллельности
прямых.

1. Подготовительная работа (рисунок на доске)

Измерить накрест лежащие углы в двух случаях
(параллельные и непараллельные прямые)

Измерьте расстояние между прямыми a и b слева и
справа от секущей. Они равны?

(С помощью наводящих вопросов, ученики сами
формулируют I признак)

Слайд №16 I признак. Если при пересечении двух
прямых третьей, накрест лежащие углы равны, то
такие прямые параллельны.

Слайд №17

VIII. Подведение итогов.

Вспомните названия углов, которые образуются
при пересечении двух прямых секущей? Как
называются углы первой группы? Второй? Третьей?

Слайд №22

IX. Рефлексия

Ребята, у каждого из вас на парте лежат три
разноцветные многоугольника. Сейчас мы вместе с
вами создадим картину, одновременно оценив урок.
Прикрепите каждый к этому листу одну из фигур,
учитывая своё отношение к уроку.

Вот и каждый из вас сегодня побыл в роли
художника- авангардиста. Вы сегодня все вместе
создали картину. А я придумала её название –
“Вдохновение геометрией”.

Слайд №23

X. Домашнее задание.

П. 24-25

• Выучить определение параллельных прямых;
• Знать названия новых углов и уметь их находить
  на рисунке.
• Выучить и уметь доказывать I признак
  параллельности прямых.
• №186 c.58

Слайд №24

Окончен урок, и выполнен план.
Спасибо, ребята, огромное вам.
За то, что упорно и дружно трудились,
И знания точно уж вам пригодились.

До новых встреч!!!

Смотрите бесплатные видео-уроки на канале Ёжику Понятно.

Содержание страницы:

Угол – геометрическая фигура, образованная двумя лучами, выходящими из одной точки.

Стороны угла – лучи, которые образуют угол.

Вершина угла – точка, из которой выходят лучи.

Угол называют тремя заглавными латинскими буквами, которыми обозначены вершина и две точки, расположенные на сторонах угла.

Важно: в названии буква, обозначающая вершину угла, стоит между двумя буквами, обозначающими точки на сторонах угла. Так, угол, изображенный на рисунке, можно назвать: ∠AOB  или ∠BOA,  но ни в коем случае не ∠OAB,∠OBA,∠ABO,∠BAO.

Величину угла измеряют в градусах. ∠AOB=24°.

Биссектриса угла – это луч с началом в вершине угла, делящий его на два равных угла.

Или

Биссектриса угла – это геометрическое место точек, равноудаленных от сторон угла.

OD – биссектриса угла ∠AOB. Она делит этот угол на два равных угла.

∠AOD=∠BOD=∠AOB2

Точка D – произвольная точка на биссектрисе. Она равноудалена от сторон OA и OB угла ∠AOB.

Вертикальные углы – пара углов, у которых стороны одного угла являются продолжением сторон второго.

Свойство: вертикальные углы равны.

Смежные углы – пара углов, у которых одна сторона общая, а две другие стороны расположены на одной прямой.

Свойство: сумма смежных углов равна 180°.

Пример:

Пары углов

(1) и (3)
(2) и (4)

называются вертикальными.

По свойству вертикальных углов:

∠COD=∠AOB
∠BOD=∠AOC

Пары углов

(1) и (2)
(2) и (3)
(3) и (4)
(4) и (1)

называются смежными.

По свойству смежных углов:

∠COD+∠DOB=180°∠DOB+∠BOA=180°∠BOA+∠AOC=180°∠AOC+∠COD=180°

Прямая, пересекающая две заданные прямые, называется секущей этих прямых.

Существует пять видов углов, которые образуются при пересечении двух прямых секущей.

Пары углов:

(1) и (5)
(2) и (6)
(3) и (7)
(4) и (8)

называются соответственными.
(Легко запомнить: они соответствуют друг другу, похожи друг на друга).

Пары углов:

(3) и (5)
(4) и (6)

называются внутренними односторонними.
(Легко запомнить: лежат по одну сторону от секущей, между двумя прямыми).

Пары углов:

(1) и (7)
(2) и (8)

называются внешними односторонними.
(Легко запомнить: лежат по одну сторону от секущей по разные стороны от двух прямых).

Пары углов:

(3) и (6)
(4) и (5)

называются внутренними накрест лежащими.
(Легко запомнить: лежат между двумя прямыми, расположены наискосок друг относительно друга).

Пары углов:

(1) и (8)
(2) и (7)

называются внешними накрест лежащими.
(Легко запомнить: лежат по разные стороны от двух прямых, расположены наискосок друг относительно друга).

Если прямые, которые пересекает секущая, параллельны, то углы имеют следующие свойства:

• Соответственные углы равны.
• Внутренние накрест лежащие углы равны.
• Внешние накрест лежащие углы равны.
• Сумма внутренних односторонних углов равна 180°.
• Сумма внешних односторонних углов равна 180°.

Сумма углов произвольного n-угольника вычисляется по формуле:

Sn=180°⋅(n−2)

где n – это количество углов в n-угольнике.

Пользуясь этой формулой, можно вычислить сумму углов для произвольного n-угольника.

Сумма углов треугольника: S3=180°⋅(3−2)=180°

Сумма углов четырехугольника: S4=180°⋅(4−2)=360°

Сумма углов пятиугольника: S5=180°⋅(5−2)=540°

Так можно продолжать до бесконечности.

Правильный многоугольник – это выпуклый многоугольник, у которого все стороны равны и все углы равны.

На рисунках изображены примеры правильных многоугольников:

Чтобы найти величину угла правильного n-угольника, необходимо сумму углов этого многоугольника разделить на количество углов.

αn=180°⋅(n−2)n

Модуль геометрия: задания, связанные с углами

Скачать домашнее задание к уроку 2.

Базисные понятия

Угол — простая фигура в геометрии, образуемая двумя лучами, следующими из некоторой точки. Эту точку определяют как его вершину. Название «угол» может относиться к части плоскости, объединяющей все лучи, исходящие из вершины фигуры. Такое обозначение может также иметь угловая мера, чаще всего определяемая в градусах.

В геометрии существует несколько критериев, позволяющих выделить разные типы угловых фигур. Они бывают тупыми и острыми, смежными или вертикальными. Для углов, образуемых в результате пересечения секущей линией двух прямых, в качестве такого критерия берется свойство взаимных соотношений формируемых при этом фигур. При рассмотрении произвольного геометрического рисунка, образованного двумя прямыми линиями и секущей, можно увидеть 4 пары соответственных, по 2 пары внутренних и внешних накрест лежащих или односторонних угловых фигур. Все эти элементы могут быть как тупоугольными, так и остроугольными.

Углы, образующиеся при пересечении прямых

Чтобы понять, как выглядят соответственные углы, а также уметь находить их на любых геометрических рисунках, нужно хорошо усвоить разницу между типами фигур, образованных секущей линией. Кроме того, следует обратить внимание на наличие внутренней и внешней областей. Первая зона ограничивается площадью между двумя прямыми, второй внешней областью считается неограниченное пространство снаружи от этих двух линий.

Итак, образованным тремя прямыми линиями угловым фигурам можно дать следующие определения:

• Накрест лежащие внутренние углы — это разносторонние по отношению к секущей объекты внутри области, сформированной прямыми. Если обе фигуры лежат за пределами двух прямых по противоположные стороны от секущей, то такие угловые элементы называются внешними накрест лежащими.
• В отличие от предыдущих противолежащих фигур, односторонние углы расположены на одной стороне: внутри области, образованной двумя прямыми (внутренние), или во внешних областях (наружные).
• Соответственные по определению являются парными фигурами, образующимися по одну сторону от линии, пересекающей две других, с аналогичных сторон обеих прямых. Один из углов пары расположен между прямыми и является внутренним, а другой лежит вне этой зоны, поэтому считается внешним.

Более наглядное представление об этом типе углов можно получить, если секущую изобразить в виде направленного вектора. Парные угловые элементы расположены в одном направлении относительно прямых, пересеченных третьей линией.

Чтобы окончательно разобраться в вопросе, нужно усвоить понятие соответствия с математической точки зрения. В геометрии это свойство двух фигур, у которых углы, стороны или точки одного объекта аналогичны соответствующим элементам другого объекта. Аналогия проявляется не в их равенстве, а во взаимном соотношении элементов. О соответствии углов говорит аналогичное пространственное положение лучей в местах пересечения прямых с третьей секущей линией. Таким образом, речь идет об элементах, имеющих одинаковое относительное положение.

Соответственные углы при параллельных прямых

Свойства фигур, формирующихся при пересечении секущей параллельных прямых, давно описаны в планиметрии. Известно, что соответственные накрест лежащие угловые элементы при параллельных прямых равны. Сложение угловых величин односторонних фигур дает значение 180 градусов. В геометрии применяется формула для расчета суммы соответственных парных угловых фигур при условии параллельности двух линий. Для определения этого параметра из числа 360 надо вычесть удвоенную угловую величину одностороннего угла, прилежащего к любому из пары рассчитываемых соответственных угловых элементов.

Равные соответственные углы указывают на параллельность прямых. Справедливость этого признака вытекает из следующих утверждений:

1. Отметим отрезок на секущей, начало и конец которого, точки C и D, находятся в местах пересечения секущей с прямыми a и b.
2. Через среднюю точку K отрезка опустим перпендикуляр к прямой a. Точки его пересечения с прямыми обозначим как A и B. Сформированные отрезками треугольники CKA и DKB являются прямоугольными, а отрезки AK и BK — сторонами, прилежащими к прямоугольным вершинам. Каждый из этих катетов одновременно является высотой треугольника, проведенной из остроугольной вершины.
3. Для доказательства следует учитывать равенство вертикальных ∠CKA и ∠DKB, ∠BDK и ∠АСК равны по условию равенства соответственных углов с учетом того, что вертикальные углы с вершинами в точках C и D равны, CK и KD — два равных отрезка по условию.
4. Таким образом, в треугольниках CKA и DKB сторона и прилежащие к ней углы имеют равные величины, что соответствует одному из признаков равенства треугольников.
5. Поскольку AB перпендикулярен прямой a и отрезку AC, то CKA — прямоугольный треугольник, и это дает основание считать, что равный ему треугольник DKB также прямоугольный, из чего следует перпендикулярность отрезка AB по отношению к прямой b.
6. Было доказано, что две прямые перпендикулярны к третьей прямой, и это подтверждает их параллельность.

Доказательство можно развернуть и в обратном направлении. Параллельные линии при пересечении третьей прямой формируют одинаковые по величине соответственные углы. Это утверждение известно как свойство параллельных линий.

Такого рода свойства встречаются в описаниях признаков и теорем. Их равенство — часть доказательств равенства и подобия треугольников. В свою очередь, используя признаки подобных и равных треугольников, можно обосновывать доказательства сложных теорем, находить решения сложных задач, править возможные ошибки.

Доказательство подобия треугольников

Существует три признака, по которым могут быть определены подобные треугольники. Во-первых, подобие подтверждается пропорциональностью всех трех сторон треугольников. Во-вторых, подобными считаются треугольники, имеющие две пропорциональные стороны, угловая величина между которыми равна соответствующему элементу второго треугольника. В-третьих, подобие подтверждается, когда имеет место равенство двух углов обоих треугольников.

Рассмотрим доказательство этого признака, в ходе которого применяется свойство тождественности соответственных угловых объектов:

1. Возьмем два треугольника ABC и A1B1C1, в которых равны два угла. Из этого следует, что величина третьего угла также одинакова в обеих фигурах. Требуется доказать подобие треугольников.
2. Отметим точку A2 на AB таким образом, чтобы величина BA2 совпала с A1B1. Через A2 параллельно основанию AC проведем прямую, проходящую через BC в точке B2.
3. Треугольники A2BC2 и A1B1C1 равны, что подтверждается одинаковыми величинами сторон A1B1, BA2 и углов B, B1 (по построению или условию), а также равенством углов A, A1 как соответственных при параллельных линиях.
4. Поскольку, согласно лемме, параллельная стороне треугольника прямая отсекает от него подобный треугольник, то A2BC2 подобен ABC. Из этого следует подобие треугольников ABC и A1B1C1.

Подобного рода рассуждения и доказательства, учитывающие свойства соответственных угловых фигур, учитываются при решении разного рода задач.

В сложных планиметрических фигурах в качестве секущей, формирующей этот тип геометрических объектов, может выступать медиана, биссектриса треугольника или какие-либо другие линии. Для решения таких задач требуется хорошее знание базовых понятий, признаков, свойств, аксиом, позволяющее заметить определенные соотношения и закономерности в том или ином задании.