Каким свойством обладают графики обратных функций
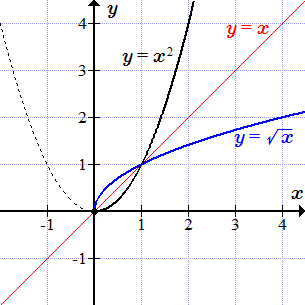
Понятие обратной функции
Допустим, что у нас есть некая функция y=f(x), которая является строго монотонной (убывающей или возрастающей) и непрерывной на области определения x∈a; b; область ее значений y∈c; d, а на интервале c; d при этом у нас будет определена функция x=g(y) с областью значений a; b. Вторая функция также будет непрерывной и строго монотонной. По отношению к y=f(x) она будет обратной функцией. То есть мы можем говорить об обратной функции x=g(y) тогда, когда y=f(x) на заданном интервале будет либо убывать, либо возрастать.
Две этих функции, f и g, будут взаимно обратными.
Для чего вообще нам нужно понятие обратных функций?
Это нужно нам для решения уравнений y=f(x), которые записываются как раз с помощью этих выражений.
Нахождение взаимно обратных функций
Допустим, нам нужно найти решение уравнения cos(x)=13. Его решениями будут все точки: x=±arсcos13+2π·k, k∈Z
Обратными по отношению друг к другу будут, например, функции арккосинуса и косинуса.
Разберем несколько задач на нахождение функций, обратных заданным.
Пример 1
Условие: какая функция будет обратной для y=3x+2?
Решение
Область определений и область значений функции, заданной в условии, – это множество всех действительных чисел. Попробуем решить данное уравнение через x, то есть выразив x через y.
Мы получим x=13y-23. Это и есть нужная нам обратная функция, но y здесь будет аргументом, а x – функцией. Переставим их, чтобы получить более привычную форму записи:
y=13x-23
Ответ: функция y=13x-23 будет обратной для y=3x+2.
Обе взаимно обратные функции можно отобразить на графике следующим образом:
Мы видим симметричность обоих графиков относительно y=x. Эта прямая является биссектрисой первого и третьего квадрантов. Получилось доказательство одного из свойств взаимно обратных функций, о котором мы поговорим далее.
Возьмем пример, в котором нужно найти логарифмическую функцию, обратную заданной показательной.
Пример 2
Условие: определите, какая функция будет обратной для y=2x.
Решение
Для заданной функции областью определения являются все действительные числа. Область значений лежит в интервале 0; +∞. Теперь нам нужно выразить x через y, то есть решить указанное уравнение через x. Мы получаем x=log2y. Переставим переменные и получим y=log2x.
В итоге у нас вышли показательная и логарифмическая функции, которые будут взаимно обратными друг другу на всей области определения.
Ответ: y=log2x.
На графике обе функции будут выглядеть так:
Основные свойства взаимно обратных функций
В этом пункте мы перечислим основные свойства функций y=f(x) и x=g(y), являющихся взаимно обратными.
Определение 1
- Первое свойство мы уже вывели ранее: y=f(g(y)) и x=g(f(x)).
- Второе свойство вытекает из первого: область определения y=f(x) будет совпадать с областью значений обратной функции x=g(y), и наоборот.
- Графики функций, являющихся обратными, будут симметричными относительно y=x.
- Если y=f(x) является возрастающей, то и x=g(y) будет возрастать, а если y=f(x) убывает, то убывает и x=g(y).
Советуем внимательно отнестись к понятиям области определения и области значения функций и никогда их не путать. Допустим, что у нас есть две взаимно обратные функции y=f(x)=ax и x=g(y)=logay. Согласно первому свойству, y=f(g(y))=alogay. Данное равенство будет верным только в случае положительных значений y, а для отрицательных логарифм не определен, поэтому не спешите записывать, что alogay=y. Обязательно проверьте и добавьте, что это верно только при положительном y.
А вот равенство x=f(g(x))=logaax=x будет верным при любых действительных значениях x.
Не забывайте про этот момент, особенно если приходится работать с тригонометрическими и обратными тригонометрическими функциями. Так, arcsinsin7π3≠7π3, потому что область значений арксинуса -π2; π2 и 7π3 в нее не входит. Верной будет запись
arcsinsin7π3=arcsinsin2π+π3==по формулепривидения=arcsinsinπ3=π3
А вот sinarcsin13=13 – верное равенство, т.е. sin(arcsin x)=x при x∈-1; 1 и arcsin(sin x)=x при x∈-π2; π2. Всегда будьте внимательны с областью значений и областью определений обратных функций!
Графики взаимно обратных функций
- Основные взаимно обратные функции: степенные
Если у нас есть степенная функция y=xa, то при x>0 степенная функция x=y1a также будет обратной ей. Заменим буквы и получим соответственно y=xa и x=y1a.
На графике они будут выглядеть следующим образом (случаи с положительным и отрицательным коэффициентом a):
- Основные взаимно обратные функции: показательные и логарифмические
Возьмем a,которое будет положительным числом, не равным 1.
Графики для функций с a>1 и a<1 будут выглядеть так:
- Основные взаимно обратные функции: тригонометрические и обратные тригонометрические
Если нам нужно построить график главной ветви синуса и арксинуса, он будет выглядеть следующим образом (показан выделенной светлой областью):
График главной ветви косинуса и арккосинуса выглядит так:
График главной ветви арктангенса и тангенса:
График главной ветви арккотангенса и котангенса будет таким:
Если же вам требуется построить обратные ветви, отличные от главных, то обратную тригонометрическую функцию при этом мы сдвигаем вдоль оси Oy на нужное число периодов. Так, если требуется обратная функция для ветви тангенса на π2; 3π2, то мы можем сдвинуть ее на величину π вдоль оси абсцисс. График будет представлять собой ветвь арктангенса, которая сдвинута на π вдоль оси ординат.
Это все свойства обратных функций, о которых мы хотели бы вам рассказать.
Источник
Определение и свойства
Определение обратной функции
Пусть функция имеет область определения X и множество значений Y. И пусть она обладает свойством:
для всех .
Тогда для любого элемента из множества Y можно поставить в соответствие только один элемент множества X, для которого . Такое соответствие определяет функцию, которая называется обратной функцией к . Обратная функция обозначается так:
.
Из определения следует, что
;
для всех ;
для всех .
Теорема о существовании и монотонности обратной функции
Если функция f строго возрастает (убывает), то существует обратная функция , которая также строго возрастает (убывает).
Доказательство
Свойство симметрии графиков прямой и обратной функций
Пусть функция f(x) определена на некотором множестве X, и имеет множество значений Y: f(X) ∈ Y. И пусть она имеет на множестве X обратную функцию f -1: f -1(Y) ∈ X. Тогда графики прямой и обратной f –1 функций, построенные при значениях их аргументов x ∈ X и x ∈ Y, соответственно, симметричны относительно прямой .
Доказательство
Теорема о существовании и непрерывности обратной функции на отрезке
Пусть функция непрерывна и строго возрастает (убывает) на отрезке . Тогда на отрезке определена и непрерывна обратная функция , которая строго возрастает (убывает).
Доказательство ⇓
Для возрастающей функции . Для убывающей – .
Теорема о существовании и непрерывности обратной функции на интервале
Пусть функция непрерывна и строго возрастает (убывает) на открытом конечном или бесконечном интервале . Тогда на интервале определена и непрерывна обратная функция , которая строго возрастает (убывает).
Доказательство ⇓
Для возрастающей функции .
Для убывающей: .
Аналогичным образом можно сформулировать теорему о существовании и непрерывности обратной функции на полуинтервале.
Если функция непрерывна и строго возрастает (убывает) на полуинтервале или , то на полуинтервале или определена обратная функция , которая строго возрастает (убывает). Здесь .
Если строго возрастает, то интервалам и соответствуют интервалы и . Если строго убывает, то интервалам и соответствуют интервалы и .
Эта теорема доказывается тем же способом, что и теорема о существовании и непрерывности обратной функции на интервале.
Примеры обратных функций
Арксинус
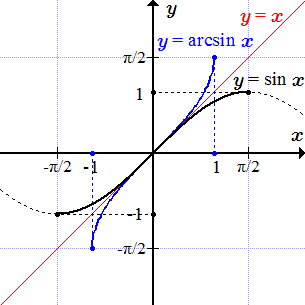
Графики y = sin x и обратной функции y = arcsin x.
Рассмотрим тригонометрическую функцию синус: . Она определена и непрерывна для всех значений аргумента , но не является монотонной. Однако, если сузить область определения, то можно выделить монотонные участки. Так, на отрезке , функция определена, непрерывна, строго возрастает и принимает значения от –1 до +1. Поэтому имеет на нем обратную функцию, которую называют арксинусом. Арксинус имеет область определения и множество значений .
Логарифм
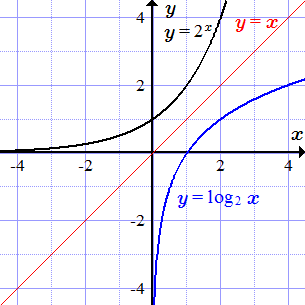
Графики y = 2x и обратной функции y = log2 x.
Показательная функция определена, непрерывна и строго возрастает при всех значений аргумента . Множеством ее значений является открытый интервал . Обратной функцией является логарифм по основанию два. Он имеет область определения и множество значений .
Квадратный корень
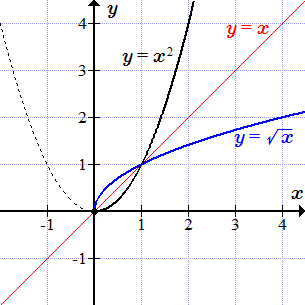
Графики y = x2 и обратной функции .
Степенная функция определена и непрерывна для всех . Множеством ее значений является полуинтервал . Но она не является монотонной при всех значений аргумента. Однако, на полуинтервале она непрерывна и строго монотонно возрастает. Поэтому если, в качестве области определения, взять множество , то существует обратная функция, которая называется квадратным корнем. Обратная функция имеет область определения и множество значений .
Пример. Доказательство существования и единственности корня степени n
Докажите, что уравнение , где n – натуральное, – действительное неотрицательное число, имеет единственное решение на множестве действительных чисел, . Это решение называется корнем степени n из числа a. То есть нужно показать, что любое неотрицательное число имеет единственный корень степени n.
Решение
Рассмотрим функцию от переменной x:
(П1) .
Докажем, что она непрерывна.
Используя определение непрерывности, покажем, что
.
Применяем формулу бинома Ньютона:
(П2)
.
Применим арифметические свойства пределов функции. Поскольку , то отлично от нуля только первое слагаемое:
.
Непрерывность доказана.
Докажем, что функция (П1) строго возрастает при .
Возьмем произвольные числа , связанные неравенствами:
, , .
Нам нужно показать, что . Введем переменные . Тогда . Поскольку , то из (П2) видно, что . Или
.
Строгое возрастание доказано.
Найдем множество значений функции при .
В точке , .
Найдем предел .
Для этого применим неравенство Бернулли. При имеем:
.
Поскольку , то и .
Применяя свойство неравенств бесконечно больших функций находим, что .
Таким образом, , .
Согласно теореме об обратной функции, на интервале определена и непрерывна обратная функция . То есть для любого существует единственное , удовлетворяющее уравнению . Поскольку у нас , то это означает, что для любого , уравнение имеет единственное решение, которое называют корнем степени n из числа x:
.
Доказательства свойств и теорем
Теорема о существовании и непрерывности обратной функции на отрезке
Все свойства ⇑ Пусть функция непрерывна и строго возрастает (убывает) на отрезке . Тогда на отрезке определена и непрерывна обратная функция , которая строго возрастает (убывает).
Доказательство
Пусть обозначает область определения функции – отрезок .
1. Покажем, что множеством значений функции является отрезок :
,
где .
Действительно, поскольку функция непрерывна на отрезке , то по теореме Вейерштрасса она достигает на нем минимума и максимума . Тогда по теореме Больцано – Коши функция принимает все значения из отрезка . То есть для любого существует , для которого . Поскольку и есть минимум и максимум, то функция принимает на отрезке только значения из множества .
2. Поскольку функция строго монотонна, то согласно теореме о существовании и монотонности обратной функции ⇑, существует обратная функция , которая также строго монотонна (возрастает, если возрастает ; и убывает, если убывает ). Областью определения обратной функции является множество , а множеством значений – множество .
3. Теперь докажем, что обратная функция непрерывна.
3.1. Пусть есть произвольная внутренняя точка отрезка : . Докажем, что обратная функция непрерывна в этой точке.
Пусть ей соответствует точка . Поскольку обратная функция строго монотонна, то есть внутренняя точка отрезка :
.
Согласно определению непрерывности нам нужно доказать, что для любого имеется такая функция , при которой
(3.1) для всех .
Заметим, что мы можем взять сколь угодно малым. Действительно, если мы нашли такую функцию , при которой неравенства (3.1) выполняются при достаточно малых значениях , то они будут автоматически выполняться и при любых больших значениях , если положить при .
Возьмем настолько малым, чтобы точки и принадлежали отрезку :
.
Введем и упорядочим обозначения:
.
Преобразуем первое неравенство (3.1):
(3.1) для всех .
;
;
;
(3.2) .
Поскольку строго монотонна, то отсюда следует, что
(3.3.1) , если возрастает;
(3.3.2) , если убывает.
Поскольку обратная функция также строго монотонна, то из неравенств (3.3) следуют неравенства (3.2).
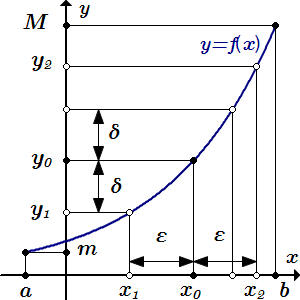
Для любого ε > 0 существует δ, так что |f -1(y) – f -1(y0)| < ε для всех |y – y0| < δ.
Неравенства (3.3) определяют открытый интервал, концы которого удалены от точки на расстояния и . Пусть есть наименьшее из этих расстояний:
.
В силу строгой монотонности , , . Поэтому и . Тогда интервал будет лежать в интервале, определяемом неравенствами (3.3). И для всех значений , принадлежащих ему будут выполняться неравенства (3.2).
Итак, мы нашли, что для достаточно малого , существует , так что
при .
Теперь изменим обозначения.
Для достаточно малого , существует такое , так что
при .
Это означает, что обратная функция непрерывна во внутренних точках .
3.2. Теперь рассмотрим концы области определения. Здесь все рассуждения остаются теми же самыми. Только нужно рассматривать односторонние окрестности этих точек. Вместо точки будет или , а вместо точки – или .
Так, для возрастающей функции , . Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Для убывающей функции , .
Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Обратная функция непрерывна в точке , поскольку для любого достаточно малого имеется , так что
при .
Теорема доказана.
Теорема о существовании и непрерывности обратной функции на интервале
Все свойства ⇑ Пусть функция непрерывна и строго возрастает (убывает) на открытом конечном или бесконечном интервале . Тогда на интервале определена и непрерывна обратная функция , которая строго возрастает (убывает).
Доказательство
Пусть обозначает область определения функции – открытый интервал . Пусть – множество ее значений. Согласно теореме о существовании и монотонности обратной функции ⇑, существует обратная функция , которая имеет область определения , множество значений и является строго монотонной (возрастает если возрастает и убывает если убывает ). Нам осталось доказать, что
1) множеством является открытый интервал , и что
2) обратная функция непрерывна на нем.
Здесь .
1. Покажем, что множеством значений функции является открытый интервал :
.
Как и всякое непустое множество, элементы которого имеют операцию сравнения, множество значений функции имеет нижнюю и верхнюю грани:
.
Здесь и могут быть конечными числами или символами и .
1.1. Покажем, что точки и не принадлежат множеству значений функции. То есть множество значений не может быть отрезком .
Если или является бесконечно удаленной точкой: или , то такая точка не является элементом множества. Поэтому она не может принадлежать множеству значений.
Пусть (или ) является конечным числом. Допустим противное. Пусть точка (или ) принадлежит множеству значений функции . То есть существует такое , для которого (или ). Возьмем точки и , удовлетворяющие неравенствам:
.
Поскольку функция строго монотонна, то
, если f возрастает;
, если f убывает.
То есть мы нашли точку, значение функции в которой меньше (больше ). Но это противоречит определению нижней (верхней) грани, согласно которому
для всех .
Поэтому точки и не могут принадлежать множеству значений функции .
1.2. Теперь покажем, что множество значений является интервалом , а не объединением интервалов и точек. То есть для любой точки существует , для которого .
Согласно определениям нижней и верхней граней, в любой окрестности точек и содержится хотя бы один элемент множества . Пусть – произвольное число, принадлежащее интервалу : . Тогда для окрестности существует , для которого
.
Для окрестности существует , для которого
.
Поскольку и , то . Тогда
(4.1.1) если возрастает;
(4.1.2) если убывает.
Неравенства (4.1) легко доказать от противного. Но можно воспользоваться теоремой о существовании и монотонности обратной функции ⇑, согласно которой на множестве существует обратная функция , которая строго возрастает, если возрастает и строго убывает, если убывает . Тогда сразу получаем неравенства (4.1).
Итак, мы имеем отрезок , где если возрастает;
если убывает.
На концах отрезка функция принимает значения и . Поскольку , то по теореме Больцано – Коши, существует точка , для которой .
Поскольку , то тем самым мы показали, что для любого существует , для которого . Это означает, что множеством значений функции является открытый интервал .
2. Теперь покажем, что обратная функция непрерывна в произвольной точке интервала : . Для этого применим предыдущую теорему ⇑ к отрезку . Поскольку , то обратная функция непрерывна на отрезке , в том числе и в точке .
Теорема доказана.
Использованная литература:
О.И. Бесов. Лекции по математическому анализу. Часть 1. Москва, 2004.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: 27-10-2018 Изменено: 10-12-2020
Источник
18.1Обратные функции
18.1.1Определение обратного отображения
Пусть отображение f:X→Y инъективно, то есть не склеивает
точки. Если представить себе его в виде картинки со стрелочками (см.
рис. 18.1 слева), это будет
означать, что нет двух стрелочек, приходящих в один и тот же элемент множества
Y. Обратим направления всех стрелочек (тот же рис. справа).
Теперь из некоторых (но может быть не
всех) точек множества Y выходит по одной стрелочке, ведущей в X. Так мы
получили новое отображение. Оно называется обратным к отображению f и
обозначается f−1.
Не нужно путать верхний индекс −1, который здесь используется, с обычной
минус первой степенью. Иными словами,
f−1(x)≠1f(x).
Какова область определения f−1? Это множество всех точек X, в которые
входит стрелочка, соответствующая отображению f. Иными словами, это множество
тех точек, в которые переходят какие-то точки из X, то есть полный образ
X под действием f. Он обозначается f(X):
f(X):={f(x)∣x∈X}⊂Y;f−1:f(X)→X.
Если отображение f биективно, то f(X)=Y и обратное
действует из Y в X.
Как записать формально, что значит, что мы «обратили стрелочки»? Возьмём любую
точку x∈X. Подействуем на неё отображеним f, получим точку f(x)∈Y.
Теперь подействуем на f(x) отображением f−1. Мы обязаны вернуться в x.
Итак, можно дать формальное определение.
Определение 1. Пусть f:X→Y — некоторое инъективное отображение. Отображение
g:f(X)→X называется обратным к отображению f, если для
всякого x∈X
g(f(x))=x.
В этом случае g обозначается через f−1.
18.1.2Обратимость и графики функций
Рассмотрим функцию f, заданную графиком. Как понять, является ли она обратимой
(то есть инъективной)? Для этого надо провести всевозможные горизонтальные
прямые и посмотреть на их точки пересечения с графиком y=f(x), см.
18.2. Если есть горизонтальные прямые, пересекающие график
в двух и более точках, функция необратима. Действительно, пусть прямая y=c
пересекает график y=f(x) в двух точках: (x1,c) и (x2,c), x1≠x2. Тогда по определению графика, это означает, что f(x1)=c и f(x2)=c, и
значит функция необратима.
Если же все горизонтальные прямые пересекают график не более, чем в одной точке,
обратная функция существует, см. рис. 18.3. Если прямая
y=c не пересекает график функции f вообще, это означает, что точка c не
лежит в области значений f и обратная функция в ней не определена. Если прямая
y=c пересекает график ровно в одной точке, обозначим эту точку через (x1,c). Тогда f(x1)=c и стало быть f−1(c)=x1. Таким образом мы однозначно
определили f−1 во всех точках, в которых эта функция определена.
Пример 1. Рассмотрим функцию f:R→R, f(x)=x2. Является
ли эта функция обратимой? Нет, не является: например, прямая y=1
пересекает график в двух точках: (−1,1) и (1,1), см.
рис. 18.4 слева.
Рис. 18.4: Функция f(x)=x2 не является обратимой всюду, но становится
обратимой, если её ограничить на неотрицательные числа
Однако, можно рассмотреть ограничение функции f на подмножество [0,+∞), то есть рассмотреть новую функцию ~f, заданную следующим
образом:
~f:[0,+∞)→R,∀x∈[0,+∞):~f(x)=g(x).
Обозначают ~f=f|[0,+∞).
Графиком ~f будет правая ветвь параболы (см. тот же рисунок,
справа), и, в отличие от исходной функции f, функция ~f является
обратимой. Её обратной является квадратный корень (вернее, арифметический
квадратный корень): ~f−1(y)=√y. Областью определения
обратной является множество [0,+∞), поскольку квадраты вещественных
чисел неотрицательны.
Вопрос 1. Найдите обратную к функции f|(−∞,0], то есть ограничению f на
множество неположительных чисел.
√x
Нет, потому что если x=−2, √x2=√4=2≠−2, то
есть мы не вернулись в ту точку, из которой вышли.
√−x
Нет. Подсказка: область определения обратной должна совпадать с областью
значения исходной функции, а область значений исходной функции
— все неотрицательные числа.
−√x
Верно, да. Для всех x≤0, (−√x)2=x.
−√−x
Нет. Подсказка: область определения обратной должна совпадать с областью
значения исходной функции, а область значений исходной функции
— все неотрицательные числа.
Вопрос 2. Рассмотрим функцию f:R→R:
f(x)=√x2
Верно ли, что f(x)=x для всех вещественных x?
Верно, посколько корень и возведение в квадрат — взаимно обратные
функции, см. замечание 1.
Нет. Найдите f(−1).
Нет, поскольку функция в левой части определена только для
неотрицательных x.
Да нет, вообще нет никаких проблем найти f(−1). Попробуйте!
Неверно, получатся разные функции.
Так и есть! При неотрицательных x равенство верно, а при x<0,
x2=(−x)2 и √x2=√(−x)2=−x (поскольку корень
обязан принимать неотрицательные значения). Значит,
√x2=|x|.
Пример 2. Функция f(x)=sinx также не является обратимой на всей области
определения, но её ограничение на отрезок [−π/2,π/2] обратимо.
Обратная к этому ограничению называется арксинусом:
arcsin:[−1,1]→[−π/2,π/2].
Рис. 18.5: Синус не является обратимой функцией, но его ограничение на
[−π/2,π/2] обратимо
Вопрос 3. Найдите обратную к функции sin|[−3π/2,−π/2].
arcsin(y+π)
Не-не-не, и у арксинуса, и у нашей обратной функции область
определения [−1,1], никакого π добавлять к аргументу не
нужно.
arcsin(y)+π
Множеством значений обратной функции является область
определения исходной. Например, если подставить y=0, получится
π, что лежит вне области определения нашей функции.
−arcsin(y)−π
Верно! Наверное, самый разумный способ понять, какой ответ
правильный, такой: построить график, провести горизонтальную
прямую y=c и отметить две точки на графике: одна соответствует
arcsin(c), а другая — искомой обратной функции. И понять, как
связаны их x-координаты.
arcsin(y)−π
Возьмём, например, y=1. Чему равняется sin(arcsin(1)−π)?
18.1.3Графики прямой и обратной функции
Если выбрать одинаковые масштабы горизонтальной и вертикальной оси и нарисовать
на одной и той же картинке графики функций y=x2, x≥0 и y=√x, мы
увидим, что они получаются друг из друга отражением относительно прямой y=x,
см. рис. 18.6 слева.
Это неудивительно: чтобы превратить график x2 в √x, нужно поменять
ролями вертикальную и горизонтальную оси, и отражение относительно y=x делает
именно это. Можно представить себе, что наша картинка нарисована на прозрачной
плёнке. Мы подняли её и повернули вокруг оси вращения, проходящей через прямую
y=x, а затем снова положили на стол. При этом координатная ось Ox легла на
место координатной оси Oy и наоборот, а кусочек параболы лёг на место графика
квадратного корня. То же самое происходит и с арксинусом (см. тот же рисунок,
справа).
Рис. 18.6: Примеры графиков функций и их обратных
Утверждение 1. Аналогичное утверждение будет верным и для любых других пар взаимно обратных
функций f и f−1.
Доказательство. Для формального доказательства нам понадобится немножко школьной
планиметрии, см. рис. 18.7.
Рис. 18.7: Иллюстрация к доказательству утверждения о симметрии графиков
Возьмём любую точку P=(x,f(x)) на графике y=f(x). Точка P′=(f(x),x)
будет принадлежать графику обратной функции, поскольку f−1(f(x))=x.
Пусть A=(0,f(x)) и A′=(f(x),0). Рассмотрим треугольники OPA и
OP′A′. Это прямоугольные треугольники, они равны по двум сторонам
(|OA|=|OA′|, |AP|=|A′P′|). Значит, |OP|=|OP′| и треугольник OPP′
равнобедренный. Прямая y=x является биссектрисой угла POP′, поскольку
она является биссектрисой прямого угла AOA′ и углы AOP и A′OP′ равны.
Значит, она является медианой и высотой треугольника OPP′. Значит отрезок
PP′ перпендикулярен бисектриссе и разбивается ей на равные отрезки. Это и
означает, что точки P и P′ симметричны относительно прямой y=x.∎
18.1.4Обратные функции и непрерывность
Утверждение 2. Пусть функиця f строго возрастает (убывает) и обратима. Тогда обратная
функция строго возрастает (убывает).
Доказательство. Рассмотрим случай когда f строго возрастает (обратный случай
рассматривается аналогично). Пусть f−1 не является строго возрастающей
функцией. Тогда найдутся точки y1 и y2, y2>y1, для которых
f−1(y2)<f−1(y1) (равенства быть не может в силу обратимости).
Но в силу возрастания f тогда
f((f−1(y2))<f(f−1(y1)).
По определению обратной функции (см. замечание 1),
f(f−1)(y2)=y2 и f(f−1)(y1)=y1. Значит y2<y1 вопреки
предположению.∎
Утверждение 3. Пусть функция непрерывна на [a,b] и обратима. Тогда f строго
монотонна на [a,b].
Доказательство. От противного. Пусть f(b)>f(a), обратный случай рассматривается аналогично.
Поскольку функция по предположению не является монотонной, она в частности не является
строго возрастающей.
Значит, найдутся такие точки x1,x2∈[a,b], что x2>x1 и
f(x2)≤f(x1). Равенства на самом деле быть не может в силу
инъективности f. Таким образом, f(x2)<f(x1). Возможно два
варианта.
Рис. 18.8: Иллюстрация к доказательству утверждения о монотонности обратимых
непрерывных функций
- Пусть f(x1)>f(a), см. рис. 18.8 слева.
Пусть y∗∈(max(f(a),f(x2)),f(x1)). По теореме о
промежуточном значении на [a,x1]
найдётся такая точка c1, что f(c1)=y∗. По той же теореме на
[x1,x2] найдётся такая точка c2, что f(c2)=y∗.
Противоречие с обратимостью. - Пусть f(x1)<f(a) (см. тот же рисунок, справа). Тогда аналогичное
рассуждение можно применить к точкам x1, x2, b. (Примените!)
Вопрос 4. На каком интервале нужно выбирать y∗ при рассмотрении второго случая?
y∗∈(f(x2),max(f(x1),f(b)))
А вот и не максимум.
y∗∈(f(x2),min(f(x1),f(b)))
Верно!
∎
Следствие 1. Пусть областью определения функции f является отрезок [a,b], функция
непрерывна и обратима и [x1,x2]⊂[a,b]. Тогда образом отрезка
[x1,x2] под действием f является отрезок с концами в точках f(x1)
и f(x2) (то есть [f(x1),f(x2)] или [f(x2),f(x1)], в зависимости
взаимного расположения f(x1) и f(x2)).
Доказательство. Нам нужно доказать два утверждения:
- Все точки y между f(x1) и f(x2) являются образами каких-то
точек x∈[x1,x2]. - Никакие другие точки не являются образами точек x∈[x1,x2].
Докажем первое утверждение. Все значения y между f(x1) и f(x2) принимаются по
теореме о промеужточном значении. Доказали.
Докажем второе. Если x1≤x≤x2 и функция строго возрастает, то
f(x1)≤f(x)≤f(x2), а если строго убывает,то f(x1)≥f(x)≥f(x2). В обоих случаях f(x) принадлежит отрезку с концами в точках
f(x1) и f(x2), и это верно для всякого x∈[x1,x2]. Тоже
доказали.∎
Следствие 2. Пусть областью определения функции f являтеся отрезок [a,b], функция
непрерывна и обратима. Пусть также [y1,y2] лежит в области значений f.
Тогда прообразом этого отрезка под действием f, то есть множеством
f−1([y1,y2]):={x∈[a,b]:f(x)∈[y1,y2]}
будет отрезок I с концами в точках f−1(y1) и f−1(y2).
Упражнение. Докажите это следствие.
Узнать ответ
По утверждению 2 обратная функция монотонна. Значит
для всех y∈[y1,y2], f−1(y) лежит между точкам f−1(y1) и
f−1(y2). То есть у любой точки y есть единственный прообраз (это
следует из обратимости), и он лежит на отрезке I (это следует из
монотонности). Значит, никакая точка вне этого отрезка не лежит в
f−1([y1,y2]). Наоборот, любая точка x∈I под действием f
переходит в точку отрезка [y1,y2] (в силу монотонности f), и значит
все такие точки x лежат в f−1([y1,y2]).
Упражнение 1. Приведите контрпримеры, демонстрирующие, что требования непрерывности и
обратимости являются существенными для двух доказанных выше следствий, то
есть что если хотя бы одно из них нарушается, утверждения перестают быть
верными. Пока вы этого не сделали, вы не можете считать, что понимаете
доказательства.
Утверждение 4. Пусть f непрерывна на [a,b] и обратима. Тогда f−1 также
непрерывна.
Доказательство. Пусть для определённости f(b)>f(a) (обратный случай рассматривается
аналогично). Тогда функция обязана возрастать: она будет монотонной в силу
обратимости, но убывать не может. Рассмотрим точку y0∈(f(a),f(b)) и
докажем, что f−1 непрерывна в y0 (односторонняя непрерывность в
концах отрезка доказывается аналогично). Пусть y0=f(x0). Мы хотим
доказать, что
limy→y0f−1(y)=f−1(y0)=x0.
Рис. 18.9: Иллюстрация к доказательству утверждения о непрерывности обратной к
непрерывной функции
Для всякого ε>0 рассмотрим интервал Uε(x0)=(x0−ε,x0+ε), см. рис. 18.9. Нам нужно доказать, что
найдётся такая окрестность ˚Uδ(y0), что все точки из этой
окрестности перейдут в Uε(x0) под действием обратного отображения
f−1. (Поскольку мы рассматриваем обратное отображение, мы, вопреки
обыкновению, ε-окрестности рисуем на горизонтальной оси, а
δ-окрестности — на вертикальной.) Будем считать, что ε
достаточно мало, чтобы Uε целиком лежал в интервале (a,b). По
следствию 1 и замечанию 2, образом
Uε под действием f является интервал V:=(f(x0−ε),f(x0+ε))
(он непуст, поскольку мы рассматриваем случай, когда f возрастает, и
значит правый конец будет правее левого). Поскольку y0=f(x0), y0∈V (в силу монотонности функции f), то есть V является окрестностью
точки y0. Поскольку под действием f окрестность Uε(x0) переходит
в окрестность V, то под действием обратного отображения f−1
окрестность (f(x0−ε),f(x0+ε)) перейдёт назад в Uε(x0).
Итак, мы получили окрестность точки f(x0), все точки из которой переходят
в ε-окрестность точки x0 под действием f−1. Это почти то, что
нам нужно. Давайте впишем в неё какую-то симметричную окрестность — она и
будет искомой δ-окрестностью (это немножко технический шаг, но в
определении предела мы используем симметричные окрестности, и нам формально
нужно получить именно такую).
Пусть δ=min(|y0−f(x0−ε)|,|y0−f(x0+ε)|)>0.
Тогда Uδ(y0)⊂(f(x0−ε),f(x0+ε)) и
f−1(Uδ(y0))⊂(x0−ε,x0+ε)=Uε(x0). (Если
всё множество V отображалось под действием f−1 в Uε(x0), то
подмножество V отображается в некоторое подмножество Uε(x0).
Таким образом, для любого y∈Uδ(y0), f−1(y)∈Uε(x0). Тем самым, построенная нами δ
удовлетворяет условию в определении искомого предела.∎
Пример 3. Мы знаем, что функция f(x)=expx=ex непрерывна и строго монотонна, её
областью определения является вся прямая и она принимает все положительные
значения. Значит, у неё существует непрерывная обратная. Она называется
натуральным логарифмом:
ln:(0,+∞)→R.
Для всех x∈R, lnex=x. Наоборот, для всех y>0, elny=y. Натуральный логарифм, так же, как и экспонента, монотонно возрастает.
Рис. 18.10: Графики экспоненты и натурального логарифма
18.2Производная обратной функции
18.2.1Мотивировка и формула
Будем использовать ту же интерпретацию производных, как в доказательстве
теоремы о производной сложной функции.
Рассмотрим две оси, x и y. Пусть f(x0)=y0. Рассмотрим небольшой отрезок
I=[x0,x0+Δx] на оси x и его образ под действием f: отрезок
f(I)=[f(x0),f(x0+Δx)] на оси y. (Для иллюстрации будем считать,
что f возрастает и Δx>0.) Тогда производная f′(x0) показывает, во
сколько (примерно) раз f(I) длиннее I, то есть во сколько раз отрезок I
растягивается отображением f, то есть f′(x0)≈|f(I)|/|I|.
Рис. 18.11: Производная функции f показывает, во сколько раз растягивается
маленький отрезок. Если f растягивает, то f−1 будет сжимать, то
есть производная обратной функции обратна к производной прямой функции.
Главное — разобраться, в каких точках эти производные нужно считать.
Посмотрим теперь на обратное отображение f−1. Оно переводит отрезок f(I)
назад в отрезок I. Когда I маленький, f(I) тоже маленький. Поэтому
(f−1)′(y0)≈|I|/|f(I)|. Обратите внимание: нам нужно брать
производную в точке, которая является концом отрезка f(I), то есть в точке
y0. Но y0=f(x0). Таким образом, можно ожидать, что
(f−1)′(f(x0))=1f′(x0).
Эту формулу мы и будем доказывать.
18.2.2Аккуратная формулировка и доказательство
Теорема 1. Пусть функция f непрерывна в окрестности точки x0 и дифференцируема
в x0. Пусть также f′(x0)≠0 и f обратима. Тогда f−1
дифференцируема в точке y0=f(x0) и
(f−1)′(f(x0))=1f′(x0).
Поскольку x0=f−1(y0), это равенство можно записать так:
(f−1)′(y0)=1f′(f−1(y0)).
Доказательство. Для упрощения формул будем обозначать f−1 через g.
Рассмотрим предел, используемый в определении производной функции
g в точке y0:
limΔy→0g(y0+Δy)−g(y0)Δy.(18.2)
Рассмотрим функцию
Δg(Δy)=g(y0+Δy)−g(y0).
В силу непрерывности g, Δg(Δy)→0 при Δy→0. Также Δg(Δy)≠0 при Δy≠0, иначе у одной точки x0 было бы два образа под действием f.
Заметим, что справедливо тождество (см. рис. 18.12):
Δy=f(x0+Δg(Δy))−f(x0).
Рис. 18.12: Иллюстрация к доказательству теоремы о производной обратной функции
Запишем теперь предел (18.2) в следующем виде:
limΔy→0g(y+Δy)−g(y)Δy=limΔy→0Δg(Δy)Δy=limΔy→01ΔyΔg(Δy)=limΔy→01f(x0+Δg(Δy))−f(x0)Δg(Δy)=…(18.3)
Рассмотрим функцию
F(Δx)=f(x0+Δx)−f(x0)Δx.
Тогда можно продолжить равенство (18.3):
…=limΔy→01F(Δg(Δy))=…(18.4)
Поскольку Δg(Δy)→0 при Δy→0 и Δg(Δy)≠0 при Δy≠0, можно воспользоваться теоремой о пределе
сложной функции (см. упражнение 2 из
лекции 13):
limΔy→0F(Δg(Δy))=limΔx→0F(Δx)=f′(x0).
Теперь можно применить теорему о пределе частного к (18.4)
(мы потребовали, чтобы f′(x0)≠0, так что делить можно) и
получить:
…=1limΔy→0F(Δg(Δy))=1f′(x0).
Теорема о пределе обратной функции доказана.∎
Пример 4. Найдём производную натурального логарифма. Известно, что (ex)′=ex.
Рассмотрим обратную функцию x=lny. Имеем:
(lny)′=1(ex)′|x=lny=1elny=1y,
где (ex)′|x=lny означает, что н
