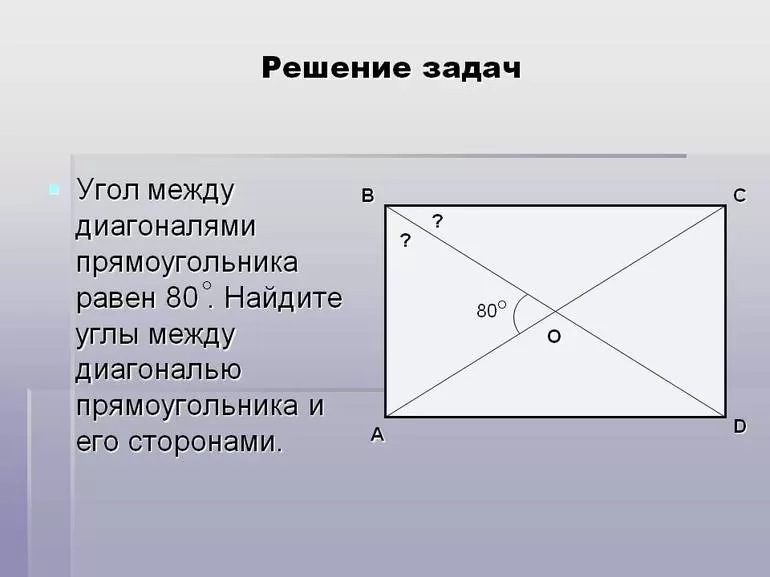
Каким свойством обладают диагонали прямоугольника

Общая информация
В задачах по геометрии и физике приходится находить некоторые параметры прямоугольника: углы, стороны, периметр, площадь и диагонали. Все эти величины связаны между собой некоторыми соотношениями. Каждый должен уметь их рассчитывать, поскольку это необходимо не только для решения математических задач, но и в жизни. Например, при укладке керамзитной плитки на пол.
Используя свойство диагоналей, можно определить метод ее укладки. Кроме того, в физике иногда требуется рассчитать площадь поперечного сечения, а необходимая формула неизвестна. Во время планирования покупки строительных материалов нужно вычислить их количество, произведя вычисление площади или периметра помещения.
Однако формул для ведения расчетов недостаточно, поскольку нужно идентифицировать геометрическую фигуру. Для каждой из них применяются разные соотношения. В случае неверного определения вычисления окажутся недостоверными, а это негативно сказывается не только на экзаменах или контрольных, но и в финансовой сфере.
Сведения о прямоугольнике

Прямоугольником называется фигура с прямыми внутренними углами между смежными сторонами, у которой противоположные стороны равны. Его частным случаем, как говорят математики, является квадрат. У него все стороны равны, а углы также являются прямыми. Не каждый может правильно определить тип фигуры, поскольку от этого шага зависит правильность вычислений какого-либо параметра.
Для каждого геометрического тела существуют определенные критерии, по которым можно узнать его принадлежность. Эти критерии называются признаками. Некоторые новички путают признаки и свойства, но существует главное отличие, которое заключено в определении терминов «признак» и «свойство». Кроме того, специалисты предлагают простой способ, позволяющий избежать путаницы между терминами.
Идентификация или признаки
Признак — некоторые критерии, по которым можно отнести фигуру к определенному типу. Свойствами называются некоторые аксиомы и утверждения, полученные при доказательстве теорем. Идентифицировать прямоугольник можно с помощью теоремы из эвклидовой геометрии. Она имеет такую формулировку: если три угла фигуры являются прямыми, то она является прямоугольником. Для доказательства нужно выполнить такие действия:
- Вычислить значение четвертого угла: D = 360 — (90 * 3) = 90 (градусов).
- Сопоставить сведения, полученные при вычислении, с определением.
Существуют также и другие признаки, по которым можно идентифицировать фигуру. По одному из них можно определить ее принадлежность к прямоугольнику. К признакам можно отнести такие:
- Равенство сторон, которые противоположны между собой.
- Внутренние углы между собой равны, а их градусная мера соответствует 90 градусам.
- Диагонали равны между собой.
- Сумма квадратов двух сторон, которые не противоположны, равна квадрату одной диагонали. Это следует из теоремы Пифагора, по которой находится одна из сторон прямоугольного треугольника.
- Если прямоугольник не является квадратом, то его стороны не равны одному значению.
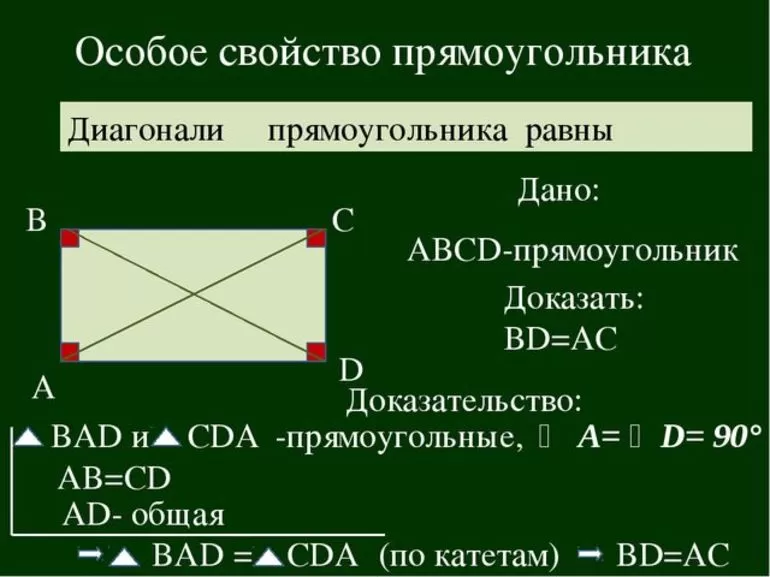
Первый и второй признаки получаются из основного определения фигуры. Третий признак является следствием доказательства теоремы, формулировка которой является следующей: диагонали прямоугольника равны. Она еще называется теоремой о диагоналях прямоугольника.
Для ее доказательства нужно начертить произвольный прямоугольник ABCD и провести в нем диагонали AC и BD. Они будут пересекаться в некоторой точке X. Они образуют прямоугольные треугольники ABC и ABD. В этом случае нужно доказать равенство треугольников. Они равны между собой: сторона АВ — общая, угол А равен В и сторона BC = AD (по равенству противоположных сторон). Из этого следует, что треугольники равны. Следовательно, их гипотенузы, которые также являются и диагоналями, равны.
Четвертый признак также доказывается. Следует рассматривать прямоугольный треугольник ABC. Используя теорему Пифагора, нужно выразить гипотенузу, которая является диагональю фигуры, через катеты (стороны фигуры): AC 2 = AB 2 + BC 2. Таким способом доказывается данный признак. Последнее утверждение получается из частного случая: если у прямоугольника все стороны равны, то он является квадратом.
Свойства фигуры
Необходимо отметить, что квадрат — правильный четырехугольник, поскольку у него все стороны равны. Результирующая формула диагонали прямоугольника будет выглядеть таким образом: d = (AB2 + BC2)^(½). При решении задач применяются свойства прямоугольника:
- Каждый из углов равен 90 градусам.
- Стороны, которые являются противолежащими и параллельными, равны.
- Сумма углов внутри фигуры составляет 360.
- Пересечение диагоналей в точке, которая делит их пополам, также является центром окружности, описанной вокруг фигуры и центром симметрии.
- Треугольники, полученные в результате проведения диагоналей, равны.
- Суммарное значение квадратичных значений всех сторон эквивалентно двойному квадрату диагонали.
- Большой и маленький треугольники, образованные диагоналями, подобны. Следует обратить внимание на коэффициент подобия.
- Диагональ эквивалентна диаметру окружности, описанной около фигуры.
- Геометрическая характеристика фигуры (сумма противоположных углов составляет 180) позволяет описать вокруг нее окружность.
- Вписать круг в прямоугольник можно тогда, когда он является правильным, т. е. ширина эквивалентна длине (квадрат).
- Угол между смежными сторонами равен 90.
- В любом прямоугольнике диагонали взаимно перпендикулярны, когда он является квадратом.
- Диагонали, пересекаясь между собой, образуют не разносторонние, а прямоугольные и равносторонние треугольники.
- Половина диагонали, проведенная из любой вершины фигуры, является медианой и высотой.
- Диагональ является биссектрисой (прямоугольник — квадрат).
- Средняя линия прямоугольника проходит через точку пересечения диагоналей.

Однако при решении задач свойств недостаточно. Для этого применяются специальные соотношения и формулы. Некоторые из них были получены из свойств фигуры. Во всех формулах будет браться радиус описанной окружности — R и ее диаметр — D, а также функция «sqrt», которая эквивалентна квадратному корню (x^(1/2) = x^(0.5)).
Периметр и площадь
Для удобства необходимо ввести некоторые обозначения. Диагонали следует обозначить литерой d, а противолежащие стороны — a и b, соответственно. Периметр — характеристика, соответствующая суммарному значению сторон фигуры. Очень часто ее обозначают литерой P. Существует также базовая формула: Р = 2а + 2b. Соотношение можно править таким способом: Р = 2 (a + b). Кроме того, существуют другие соотношения для определения P, когда известны некоторые параметры:
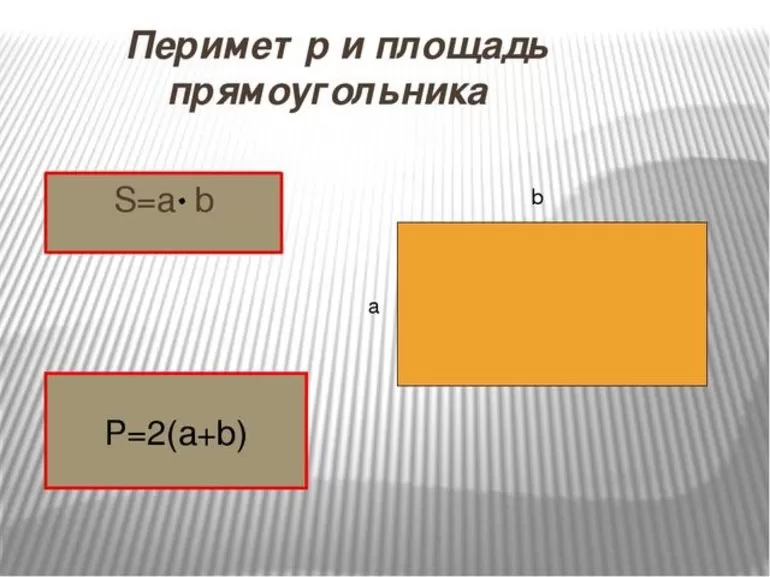
- Величина площади и сторона, которая известна: P = (2S + 2a 2 ) / a или P = (2S + 2b 2 ) / b.
- Диагональ и a (b): P = 2(a + (d 2 — a 2 )^(0.5)) = 2(b + (d 2 — b 2 )^(0.5)).
- a (b) и R: P = 2(a + (4 * R 2 — a 2 )^(0.5)) = 2(b + (4 * R 2 — b 2 )^(0.5)).
- D и a (b): P = 2(a + sqrt(D 2 — a 2 )) = 2(b + sqrt(D 2 — b 2 )).
Площадь — характеристика размерности двумерной фигуры. Ее обозначают литерой S, и измеряют в метрических единицах в квадрате (мм 2, см 2, м 2 и т. д.). Следует отметить, что она вычисляется интегральным методом. Однако для частных случаев существуют соотношения. Формула, которая является основанием для всех остальных соотношений, называется базовой. Она имеет такой вид: S = a * b. Площадь находится в зависимости от параметров, которые известны:
P и a (b): S = [(P * a) — 2a 2 ] / 2 = [(P * b) — 2b 2 ] / 2.
a (b) и d: S = a * sqrt[d 2 — a 2 ] = b * sqrt[d 2 — b 2 ].
Синус острого угла (Y) между двумя d и d: S = d 2 * sin (Y) / 2.
R и a (b): S = a * sqrt[4 * R 2 — a 2 ] = b * sqrt[4 * R 2 — b 2 ].
D и a (b): S = a * sqrt[D 2 — a 2 ] = b * sqrt[D 2 — b 2 ].
Для решения различных задач также могут быть полезны и другие соотношения, позволяющие найти не только диагонали, но и стороны прямоугольника.
Диагонали и стороны
Для оптимизации решения нужно знать формулы, с помощью которых можно находить одну из сторон или диагональ прямоугольника. Необходимо разобрать основные соотношения, по которым находятся стороны фигуры, когда известны следующие параметры:
- d и a (b): a = sqrt[d 2 — b 2 ] и b = sqrt[d 2 — a 2 ].
- S и a (b): a = S / b и b = S / a.
- P и a (b): a = (P — 2b) / 2 и b = (P — 2a) / 2.
Для нахождения диагонали также есть некоторые формулы. Для их применения следует знать такие параметры фигуры:
a и b: d = [a 2 + b 2 ]^(1/2).
S и a (b): d = (S 2 + a 4 )^(1/2) / a= (S 2 + b 4 )^(1/2) / b.
P и a (b): d = (P 2 — 4Pa + 8a 2 )^(1/2) / 2 = (P 2 — 4Pb + 8b 2 )^(1/2) / 2.
- R и D: d = 2R и d = D.
Однако это не все соотношения. В некоторых случаях разрешается описывать окружность вокруг фигуры. С помощью такого «геометрического хода» можно существенно упростить решение задачи. Это позволяет воспользоваться другими формулами.
Другие соотношения
Для решения задач используются и другие соотношения, которые позволяют найти параметры окружности, которая описана. Пусть дана окружность с радиусом R и диаметром D. Кроме того, известны некоторые параметры фигуры (a, b, d, P и S). С помощью формул можно найти D и R окружности при известных некоторых величинах:
a и b: R = (a 2 + b 2 )^(1/2) / 2.
P и a (b): R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (P 2 — 4Pb + 8b 2 )^(1/2) / 4.
S и a (b): R = (S 2 + a 4 )^(1/2) / 2a = (S 2 + b 4 )^(1/2) / 2b.
- d: R = d / 2.
- sin(F), прилегающего к диагонали и стороне, и a: R = a / 2sin (F).
- cos(F) и b: R = b / 2cos (F).
Для нахождения угла F следует воспользоваться такой формулой: sin (F) = a / d и cos (F) = b / d. Острый угол между двумя диагоналями определяется при помощи такого соотношения: sin (Y) = 2S / d 2 .
Пример решения
Пусть дана некоторая фигура, диагонали которой равны, а ее периметр равен 50. Одна из сторон a = 10. Следует провести идентификацию, а также найти такие параметры:

- Другие стороны.
- Значения диагоналей.
- Площадь.
- R описанной окружности через площадь и периметр.
- Выяснить возможность укладки плитки в форме квадрата на такую поверхность.
- Вычислить значения всех углов между смежными сторонами.
Данная задача является типом сложного класса, поскольку название фигуры не упоминается. Ее следует идентифицировать, а затем применить некоторые формулы для решения. Кроме того, необходимо верно выполнить 5 пункт. Однако не следует углубляться в строительную сферу. Бывают два метода укладки плитки: обычный — форма помещения является прямоугольником или квадратом, и с центра — другая фигура.
У фигуры диагонали равны, значит по третьему признаку она является прямоугольником. К нему можно применять вышеописанные формулы. Для нахождения другой стороны следует составить уравнение 2x + 2 * 10 = 50. Затем нужно перенести все известные значения в правую часть: 2х = 50 — 20. Далее можно найти переменную: х = 30 / 2 = 15 (ед.). Следует обратить внимание на написание единицы измерения. Если в условии задачи она не указана, то пишется единица измерения, которая заключается в круглые скобки. Достаточно найти только одну сторону, поскольку у прямоугольника существует свойство равенства противоположных сторон.
Значение диагоналей находится по формуле: d = [a 2 + b 2 ]^(1/2) = (15 2 + 10 2 )^(1/2) = (225 +100)^(1/2) = (325)^(1/2). Площадь можно найти таким образом: S = a * b = 15 * 10 = 150 [(ед.)^2]. Радиус вычисляется так:
R = (P 2 — 4Pa + 8a 2 )^(1/2) / 4 = (50 2 — 4 * 50 * 10 + 8 * 10 2 )^(1/2) / 4 = (1300)^(1/2) / 4 (ед.).
R = (S 2 + a 4 )^(1/2) / 2a = (150 2 + 100 4 )^(1/2) / (2 * 10) = (1300)^(1/2) / 4 (ед.).
Плитку можно укладывать обыкновенным способом, начиная не с центра, поскольку поверхность является прямоугольником. Все углы между сторонами равны между собой. Их градусная мера по 12 свойству соответствует 90.
Таким образом, при решении задач рекомендуется идентифицировать геометрическую фигуру, а затем применять к ней формулы.
Источник
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы расскажем об одной из основных геометрических фигур – ПРЯМОУГОЛЬНИКЕ.
Название это весьма говорящее, и в нем скрыто официальное определение.
Прямоугольник – это четырехугольник, у которого все углы прямые, то есть равны 90 градусам.
Впервые описание этой фигуры встречается еще в Древнем Египте. Но в те времена все геометрические правила давались как неопровержимые истины, не предоставляя доказательств.
Более правильный подход появился в Древней Греции. И естественно, автором стал самый знаменитый математик той эпохи — Евклид. А прямоугольник, как и многие другие фигуры и термины, был подробно описан в его произведении «Начала».
Прямоугольник — это…
Все тот же Евклид разделил все четырехугольники на два вида – параллелограммы (что это?) и трапеции (что это?).
У первых противоположные стороны равны и параллельны, а у вторых параллельна только одна пара сторон, и они при этом не равны.
То есть выглядит это так:
Так вот, прямоугольник в данном случае является частным случаем параллелограмма.
Судите сами:
У этой фигуры противоположные стороны параллельны. Это первое условие по Евклиду. И к тому же они равны, что является условием номер два.
У прямоугольника есть и собственный частный случай. Когда равны не только противоположные стороны, а все. И как нетрудно догадаться, фигура эта называется квадрат.
Ну, и логично предположить, что квадрат (как и сам прямоугольник) является частным случаем параллелограмма.
Признаки прямоугольника
Признаки геометрической фигуры – это совокупность отличий, по которым ее можно выделить среди других.
В случае с прямоугольником их всего три:
- Если один из углов параллелограмма прямой, то данный параллелограмм является прямоугольником.
- Если три угла четырехугольника являются прямыми, то перед нами опять же прямоугольник. При этом нет необходимости доказывать, что четырехугольник является параллелограммом. Это промежуточное звено становится верно само по себе.
- Если диагонали параллелограмма равны между собой, то фигура точно является прямоугольником.
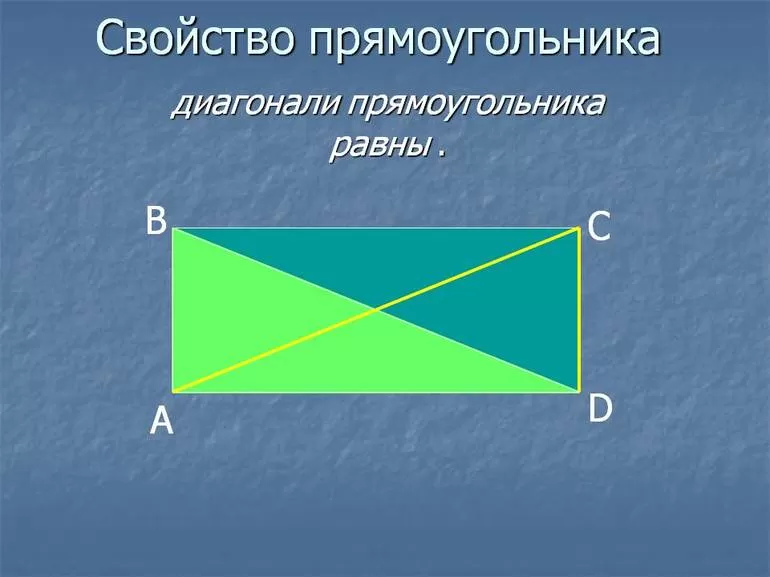
Диагонали прямоугольника
Как мы уже упомянули выше, диагонали прямоугольника (отрезки, соединяющие его противоположные углы) равны между собой.
Доказать это можно с помощью известной теоремы Пифагора. Она гласит, что «Сумма квадратов катетов прямоугольного треугольника равна квадрату гипотенузы».
В нашем случае гипотенузой является диагональ прямоугольника, которая делит его на два равных прямоугольных треугольника. И теорема Пифагора выглядит следующим образом:
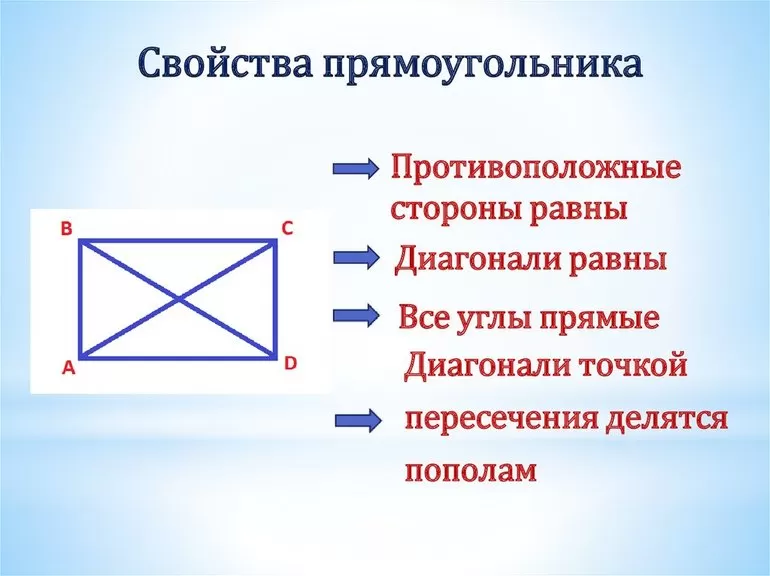
Свойства прямоугольника
К свойствам прямоугольника относятся следующие утверждения:
- Прямоугольник является параллелограммом, а значит имеет все присущие ему свойства.
- У прямоугольника равны противоположные стороны.
- У прямоугольника противоположные стороны параллельны.
- У прямоугольников все прилегающие друг к другу стороны пересекаются под прямыми углами. А в сумме они дают 360 градусов.
- У прямоугольников обе диагонали равны между собой.
- Диагональ прямоугольника делит фигуру ровно пополам, и в результате получаются два одинаковых прямоугольных треугольника.
- Диагонали прямоугольника пересекаются в его геометрическом центре. А их точка пересечения делит каждую диагональ на два равных отрезка. Более того, все четыре отрезка равны между собой.
- У прямоугольника точка пересечения диагоналей является еще и центром описанной вокруг окружности. Причем длина диагонали одновременна является диаметром (что это такое?) этой окружности.
Периметр и площадь
Для того чтобы определить периметр прямоугольника, надо просто сложить длины всех его четырех сторон.
Но с учетом того, что попарно они равны, то конечная формула может выглядеть более просто:
Площадь прямоугольника вычисляется также весьма просто. Надо лишь перемножить две его стороны:
К слову, это не единственная формула для вычисления площади. Площадь также можно получить, имея значение периметра фигуры или длину его диагонали. Но эти формулы гораздо сложнее.
Вот и все, что мы хотели рассказать о геометрической фигуре ПРЯМОУГОЛЬНИК. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Использую для заработка
- ВоркЗилла – удаленная работа для всех
- Анкетка – платят за прохождение тестов
- Etxt – платят за написание текстов
- Кьюкоммент – биржа комментариев
- Поиск лучшего курса обмена
- 60сек – выгодный обмен криптовалют
- Бинанс – надёжная биржа криптовалют
- ВкТаргет – заработок в соцсетях (ВК, ОК, FB и др.)
Источник
Планируемый результат.
Учащиеся узнают, что такое диагональ, научатся проводить диагонали в многоугольниках, познакомятся со свойствами диагоналей квадрата и прямоугольника, вычислят периметр и площадь квадрата и прямоугольника.
Тип урока – изучение нового учебного материала.
Техническое обеспечение урока – компьютер, интерактивная доска IQ Board, электронное приложение к учебнику Г.В. Дорофеева, Т.Н. Мираковой «Математика», 4 класс, М., «Просвещение», 2014 год.
Оборудование: учебник Г.В. Дорофеева, Т.Н. Мираковой «Математика», 4 класс, М., «Просвещение», 2014 год, маркеры, карточки для выполнения заданий, конверты с геометрическими фигурами, ножницы, коробка с геометрическими фигурами для жеребьёвки.
Отгадывание загадок. Решение задач на нахождение площади и периметра.
Этапы урока
Ход урока
Характеристика деятельности учителя и учащихся
Организационный момент.
Математика пришла,
Занимай свои места!
Математика сложна,
Но скажу с почтением:
Математика нужна
Всем без исключения!
Начинаем мы опять
Решать, отгадывать, смекать!
– Работать мы будем группами. Состав каждой группы определяется с помощью жеребьёвки. Вытянув геометрические фигуры из коробки, ребята распределяются на группы.
Проводится жеребьёвка. В коробке вырезаны из картона геометрические фигуры ( пятиугольник, круг, трапеция). Вынимая фигуру, ребёнок называет её и отправляется в свою группу.
Актуализация знаний учащихся.
- Отгадывание загадок. Решение задач на нахождение площади и периметра.
Работа в группах.
Учитель читает загадку. Группа, отгадавшая загадку, получает от учителя задание для выполнения. Задание выполняется в группе, на листе бумаге маркером.
Цель:
Актуализировать знания о многоугольниках и их вершинах. Характеризовать св-ва геометрических фигур.
Закреплять умение вычислять периметр треугольника и периметр и площадь прямоугольника.
Уметь выполнять взаимооценку учебного задания и оказывать необходимую взаимопомощь
Применять простейшие приёмы ораторского искусства и оценивать своё умение это делать. Применять изученные способы действий для решения задач в типовых и поисковых ситуациях
Фронтальная работа.
Выполнив задание, учащиеся представляют свою работу на доске. Представитель от группы рассказывает способ решения.
Цель:
Знать формулы площади и периметра прямоугольника (S = а • Ь, Р = (о + Ь) • 2), площади и периметра квадрата (S = а -а, Р = 4 • а)и уметь их применять при решении задач.
Работать в группах: распределять роли между членами группы, планировать работу, распределять виды работ, определять сроки, представлять результаты с помощью сообщений, рисунков, средств ИКТ, оценивать результат работы.
Формулировать в рамках учебного диалога понятные высказывания, используя термины..
Самоопределение к деятельности
- Посмотрите на доску. (Слайд №1)
– Что изображено?
– Как называются эти фигуры?
– Какую из этих фигур можно назвать лишней? Почему? (дети высказывают предположения: классификация по цвету, по форме и пр.)
- Начертите себе в тетрадь такие фигуры.
– Соедините противоположные вершины многоугольников, которые не лежат на одной стороне, отрезками.
– Назовите эти отрезки у прямоугольника, квадрата, многоугольника.
– Почему нет такого отрезка у треугольника? (нет противоположной вершины, не лежащей на одной стороне)
– Кто знает, как называется такой отрезок? (дети высказывают предположения)
– Что узнаем на уроке? (Узнаем как называется отрезок, соединяющий противоположные вершины многоугольников, которые не лежат на одной стороне.)
Фронтальная работа.
Работа на интерактивной доске.
Цель:
Классифицировать множество объектов по свойству и оценивать своё умение это делать (на основе применения соответствующих эталонов)
Уметь строить отрезки, определять виды углов многоугольника, уметь распознавать геометрические фигуры и чертить фигуры на клетчатой бумаге
Физ минутка.
«Мишка-панда»
Цель:
снятие эмоционального и мышечного напряжения, контролировать своё поведение и общение с нормами социума.
Работа по теме урока
- Работа с учебником.
– Прочитайте определение на с.23.
– О каком отрезке идёт речь? Как он называется?
– Почему у треугольника не может быть диагонали?
– Взгляните на доску ещё раз. Какую фигуру можно назвать лишней и почему?
- Практическая работа «Свойства диагоналей прямоугольника и квадрата»
– Вам предстоит работа в группах, будьте терпимы друг к другу, уважайте мнение другого, если даже с вашей точкой зрения не совпадает.
Фронтальная работа.
Цель:
научить использовать приобретённые знания и умения в практической деятельности, осуществлять взаимный контроль, приходя к единому мнению, адекватно взаимодействовать с партнёром в рамках учебного диалога.
1 группа.
2 группа.
3 группа.
Работа в группах.
Цель:
Уметь пользоваться изученной математической терминологией. Работать с информацией
Проводить диагонали многоугольника. Характеризовать свойства диагоналей прямоугольника, квадрата. Исследовать фигуру, выявлять свойства ее элементов, высказывать суждения и обосновывать или опровергать их.
Составлять инструкцию, план решения, алгоритм выполнения задания
Уметь действовать согласно инструкции.
Выполнив задание, учащиеся представляют свою работу на интерактивной доске. (Слайд №2). Представитель от группы рассказывает способ решения.
Выполняет задание из учебника №1 с.23.
Вывод: Диагонали прямоугольника равны.
Вывод: Диагонали прямоугольника точкой пересечения делятся попалам.
1. Возьмите из конверта синий прямоугольник. Соедините отрезком противоположные вершины и разрежьте прямоугольник по диагонали (нижняя левая вершина и верхняя правая).
2. Возьмите второй синий прямоугольник и проведите диагональ из верхнего левого угла в нижний правый. Разрежьте прямоугольник по диагонали.
3. Сравните длины диагоналей прямоугольника путем наложения.
4. Обоснуйте свой вывод.
Вывод: Диагональ делит прямоугольник на два треугольника.
Вывод: Диагонали прямоугольника равны.
1.Возьмите красный прямоугольник. Проведите в нем диагонали (соедините отрезком противоположные вершины). Укажите точку пересечения отрезков.
2. Разрежьте прямоугольник по диагоналям на отрезки.
3. Сколько треугольников получилось?
4. Наложите их попарно так, чтобы точка пересечения была вершинами тупоугольных треугольников и остроугольных.
5. Накладывая треугольники друг на друга, сравните стороны, идущие от вершин.
6. Обоснуйте свой вывод.
Вывод: Отрезки, полученные при пересечении диагоналей, равны.
Вывод: Диагонали делят прямоугольник на 4 треугольника
Первичное закрепление.
- Самостоятельная работа.
№2 с.24
Цель:
Выполнять учебное задание, используя свойства диагоналей. Уметь решать задачи арифметическим способом
Рефлексия
Выполнение заданий из электронного приложения к учебнику.
– Кто доволен своей работой на уроке?
Фронтальная работа.
Цель:
понимание собственных достижений и достижений команды, навыки взаимодействия в коллективе.
Итог урока
– Что вам понравилось на уроке?
-Что было трудно?
– Где можно применить полученные знания? (на уроках ИЗО, технологии, в строительстве, при пошиве одежды, в архитектуре и пр.)
Цель:
Анализировать житейские ситуации, формировать интерес к изучаемому материалу.
Домашнее задание.
№8, №9 с.24.
Цель:
Выполнять учебное задание, используя свойства диагоналей. Уметь решать задачи арифметическим способом
Г.В.Дорофеев ,Т.Н. Миракова «Уроки математики». 4 класс, М.: Просвещение, 2013 год.
Т.Н. Максимова «Поурочные разработки по математике» 3 класс к УМК Л.Г. Петерсон, М. «Вако», 2013 год.
Т.Н. Максимова «Поурочные разработки по математике» 4 класс к УМК Л.Г. Петерсон, М. «Вако», 2013 год.
Источник
