Каким свойством обладает средняя линия треугольника трапеции

Серединный отрезок
Трапеция — фигура (четырехугольник), что состоит из четырех сторон, две из которых лежат на параллельных прямых, а остальные нет. Параллельные — верхнее и нижнее основание, 2 другие имеют название боковых сторон. Из этого следует, что четырехугольник состоит из двух оснований.
Средняя линия — отрезок, который соединяет середины боков фигуры и обозначается буквой m. Интересно, что если в треугольнике таких отрезков можно провести 3, то в таком четырёхугольнике исключительно одну.
Свойство и формулы
Серединная линия равняется половине сумм длины двух оснований. Это определение является теоремой, доказательство и для того чтобы его сформулировать, необходимо обратить внимание на свойство срединного отрезка в треугольнике.
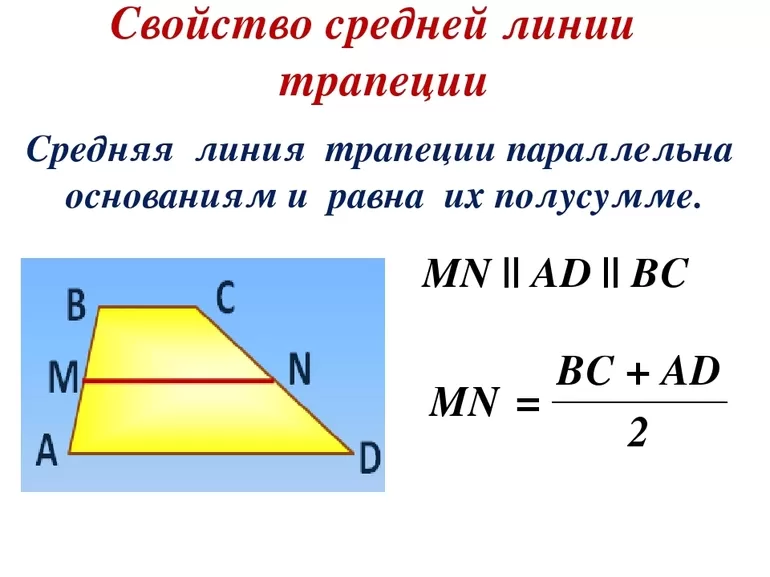
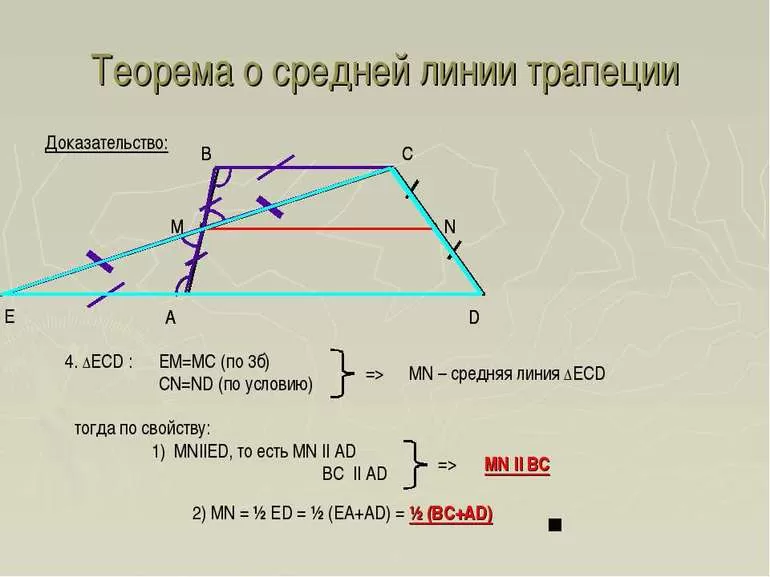
Доказать теорему просто. Для этого в трапеции проводят серединный отрезок так, чтобы он опускался с верхней точки фигуры и пересекался с продленным нижним основанием. Такая линия делит четырёхугольник на два треугольника. Причем средняя линия фигуры также принадлежит треугольнику и выполняет те же функции. Она равна половине нижней стороны, которая состоит из двух отрезков, равных основаниям трапеции.
Свойство такого отрезка — в четырехугольнике он параллелен основаниям. Учитывая эти данные, их можно использовать как признак при решениях различных заданий для выявления этого понятия.
Формула для нахождения записывается так:
m = (a + b) / 2, где a, b — обозначение длины оснований.
Тригонометрия углов применима в формуле:
- m = a — h (ctga +ctg b)/ 2;
- m = b — h (ctga +ctg b)/ 2.
Полусумма оснований трапеции вычисляется через диагонали и их угол пересечения и высоту. Итак, для этого находится:
- m = d 1 d 2 /2 h * sina;
- m = d 1 d 2 /2 h * sinb.
Углы а, b находятся при нижнем основании, а линия h является высотой, проведенной к этому отрезку.
Формула средней линии трапеции через площадь и высоту записывается так:
m = S / h.
Кроме этого, такой отрезок делит фигуру на две части и имеет место соотношение их площадей, которое выражается в виде:
S 1 /S 2 =3a+b/a+3b, где основания a<b.
Все эти формулы используются для решения задач и доказывания определённых утверждений.
Примеры заданий
Серединный отрезок трапеции равен 15 дм, а одно из оснований на 6 дм длиннее от другого. Определить длину параллельных сторон в трапеции.
Чтобы найти нужные стороны, нужно припустить, что на одну приходится х дм, соответственно на другую — (х+6) дм. Учитывая свойство серединного отрезка в этой фигуре, следует, что m = a + b /2.
m =2х+6/2=15, от сюда следует, что х=12 дм.
В результате a =12 дм, b =18 дм.
Следующее задание, где требуется искать стороны, что лежат на параллельных прямых. При этом дано их соотношения 4:7 средняя линия равна 55 дм.
Итак, пусть k — коэффициент пропорциональности, основания относятся как 4 k :7 k. Получается уравнение (4k +7k)/2=55. Отсюда следует, что k =10, то есть на нужные отрезки приходится по 40 и 70 дм.
Таким образом, средняя линия треугольника и трапеции имеет одинаковое свойство. Темы между собой очень похожи. Следовательно, средняя линия трапеции равна половине сумм двух оснований.
Источник
[{Large{text{Произвольная трапеция}}}]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна (180^circ).
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
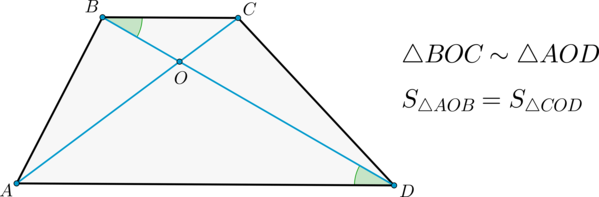
Доказательство
1) Т.к. (ADparallel BC), то углы (angle BAD) и (angle ABC) – односторонние при этих прямых и секущей (AB), следовательно, (angle
BAD
+angle ABC=180^circ).
2) Т.к. (ADparallel BC) и (BD) – секущая, то (angle DBC=angle
BDA) как накрест лежащие.
Также (angle BOC=angle AOD) как вертикальные.
Следовательно, по двум углам (triangle BOC sim triangle AOD).
Докажем, что (S_{triangle AOB}=S_{triangle COD}). Пусть (h) – высота трапеции. Тогда (S_{triangle ABD}=frac12cdot hcdot
AD=S_{triangle ACD}). Тогда: [S_{triangle AOB}=S_{triangle ABD}-S_{triangle AOD}=S_{triangle ACD}-S_{triangle AOD}=S_{triangle
COD}]
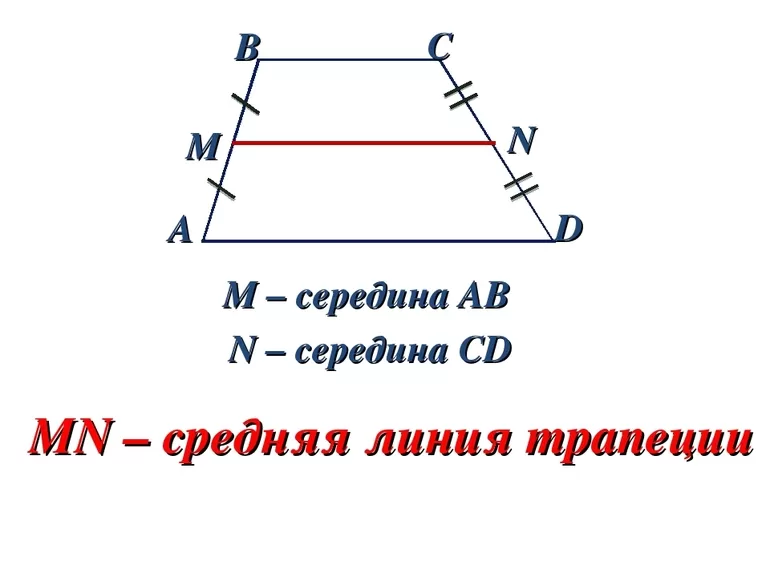
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
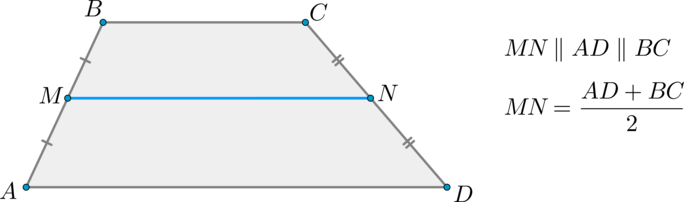
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем параллельность.
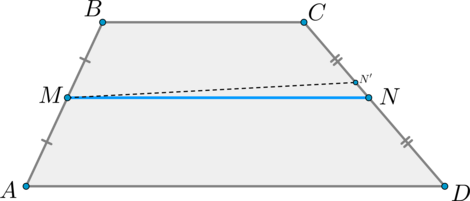
Проведем через точку (M) прямую (MN’parallel AD) ((N’in CD)). Тогда по теореме Фалеса (т.к. (MN’parallel ADparallel BC, AM=MB)) точка (N’) — середина отрезка (CD). Значит, точки (N) и (N’) совпадут.
2) Докажем формулу.
Проведем (BB’perp AD, CC’perp AD). Пусть (BB’cap MN=M’, CC’cap
MN=N’).
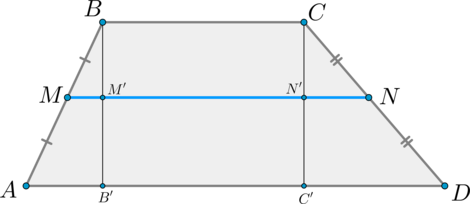
Тогда по теореме Фалеса (M’) и (N’) — середины отрезков (BB’) и (CC’) соответственно. Значит, (MM’) – средняя линия (triangle
ABB’), (NN’) — средняя линия (triangle DCC’). Поэтому: [MM’=dfrac12 AB’, quad NN’=dfrac12 DC’]
Т.к. (MNparallel ADparallel BC) и (BB’, CC’perp AD), то (B’M’N’C’) и (BM’N’C) – прямоугольники. По теореме Фалеса из (MNparallel AD) и (AM=MB) следует, что (B’M’=M’B). Значит, (B’M’N’C’) и (BM’N’C) – равные прямоугольники, следовательно, (M’N’=B’C’=BC).
Таким образом:
[MN=MM’+M’N’+N’N=dfrac12 AB’+B’C’+dfrac12 C’D=] [=dfrac12 left(AB’+B’C’+BC+C’Dright)=dfrac12left(AD+BCright)]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
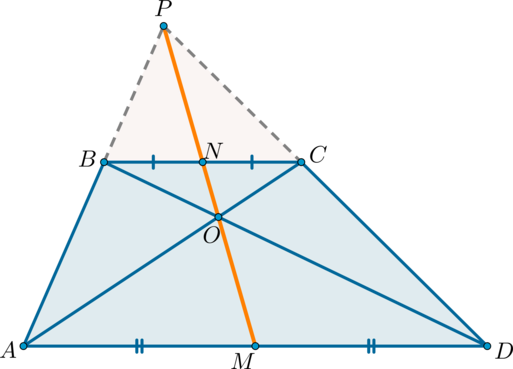
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки (P), (N) и (M) лежат на одной прямой.
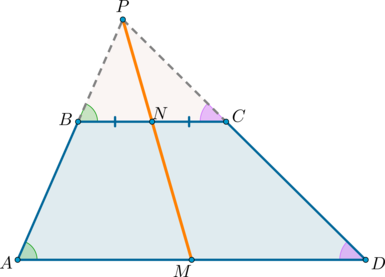
Проведем прямую (PN) ((P) – точка пересечения продолжений боковых сторон, (N) – середина (BC)). Пусть она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
Рассмотрим (triangle BPN) и (triangle APM). Они подобны по двум углам ((angle APM) – общий, (angle PAM=angle PBN) как соответственные при (ADparallel BC) и (AB) секущей). Значит: [dfrac{BN}{AM}=dfrac{PN}{PM}]
Рассмотрим (triangle CPN) и (triangle DPM). Они подобны по двум углам ((angle DPM) – общий, (angle PDM=angle PCN) как соответственные при (ADparallel BC) и (CD) секущей). Значит: [dfrac{CN}{DM}=dfrac{PN}{PM}]
Отсюда (dfrac{BN}{AM}=dfrac{CN}{DM}). Но (BN=NC), следовательно, (AM=DM).
2) Докажем, что точки (N, O, M) лежат на одной прямой.
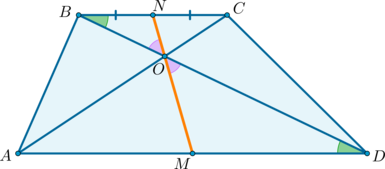
Пусть (N) – середина (BC), (O) – точка пересечения диагоналей. Проведем прямую (NO), она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
(triangle BNOsim triangle DMO) по двум углам ((angle OBN=angle
ODM) как накрест лежащие при (BCparallel AD) и (BD) секущей; (angle BON=angle DOM) как вертикальные). Значит: [dfrac{BN}{MD}=dfrac{ON}{OM}]
Аналогично (triangle CONsim triangle AOM). Значит: [dfrac{CN}{MA}=dfrac{ON}{OM}]
Отсюда (dfrac{BN}{MD}=dfrac{CN}{MA}). Но (BN=CN), следовательно, (AM=MD).
[{Large{text{Равнобедренная трапеция}}}]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию (ABCD).
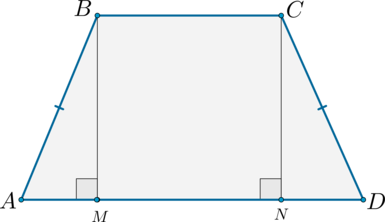
Из вершин (B) и (C) опустим на сторону (AD) перпендикуляры (BM) и (CN) соответственно. Так как (BMperp AD) и (CNperp AD), то (BMparallel CN); (ADparallel BC), тогда (MBCN) – параллелограмм, следовательно, (BM = CN).
Рассмотрим прямоугольные треугольники (ABM) и (CDN). Так как у них равны гипотенузы и катет (BM) равен катету (CN), то эти треугольники равны, следовательно, (angle DAB = angle CDA).
2) 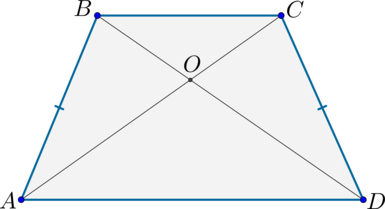
Т.к. (AB=CD, angle A=angle D, AD) – общая, то по первому признаку (triangle ABD=triangle ACD). Следовательно, (AC=BD).
3) Т.к. (triangle ABD=triangle ACD), то (angle BDA=angle CAD). Следовательно, треугольник (triangle AOD) – равнобедренный. Аналогично доказывается, что и (triangle BOC) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
Рассмотрим трапецию (ABCD), такую что (angle A = angle D).
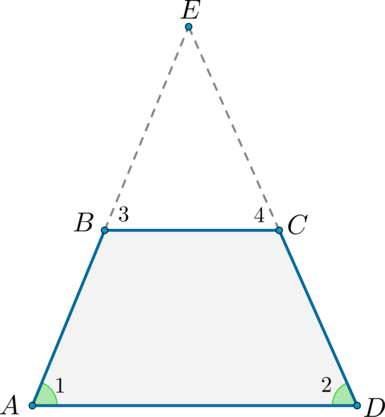
Достроим трапецию до треугольника (AED) как показано на рисунке. Так как (angle 1 = angle 2), то треугольник (AED) равнобедренный и (AE
= ED). Углы (1) и (3) равны как соответственные при параллельных прямых (AD) и (BC) и секущей (AB). Аналогично равны углы (2) и (4), но (angle 1 = angle 2), тогда (angle 3 = angle 1 = angle 2 =
angle 4), следовательно, треугольник (BEC) тоже равнобедренный и (BE = EC).
В итоге (AB = AE – BE = DE – CE = CD), то есть (AB = CD), что и требовалось доказать.
2) Пусть (AC=BD). Т.к. (triangle AODsim triangle BOC), то обозначим их коэффициент подобия за (k). Тогда если (BO=x), то (OD=kx). Аналогично (CO=y Rightarrow AO=ky).
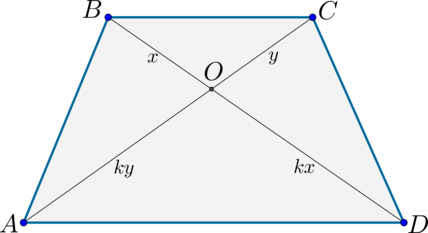
Т.к. (AC=BD), то (x+kx=y+ky Rightarrow x=y). Значит (triangle AOD) – равнобедренный и (angle OAD=angle ODA).
Таким образом, по первому признаку (triangle ABD=triangle ACD) ((AC=BD, angle OAD=angle ODA, AD) – общая). Значит, (AB=CD), чтд.
Источник
Средняя линия фигур в планиметрии — отрезок, соединяющий середины двух сторон данной фигуры. Понятие употребляется для следующих фигур: треугольник, четырёхугольник, трапеция.
Средняя линия треугольника[править | править код]
Средняя линия треугольника
Средняя линия треугольника — отрезок, соединяющий середины двух сторон этого треугольника[1].
Свойства[править | править код]
- средняя линия треугольника параллельна основанию и равна его половине.
- средняя линия отсекает треугольник, подобный и гомотетичный исходному с коэффициентом 1/2; его площадь равна одной четвёртой площади исходного треугольника.
- три средние линии делят исходный треугольник на четыре равных треугольника. Центральный из этих треугольников называется дополнительным или серединным треугольником.
Признаки[править | править код]
- Если отрезок в треугольнике проходит через середину одной из его сторон, пересекает вторую и параллелен третьей, то этот отрезок – средняя линия.
Средняя линия четырёхугольника[править | править код]
Средняя линия четырёхугольника — отрезок, соединяющий середины противолежащих сторон четырёхугольника.
Свойства[править | править код]
Первая линия соединяет 2 противоположные стороны.
Вторая соединяет 2 другие противоположные стороны.
Третья соединяет центры двух диагоналей (не во всех четырёхугольниках диагонали пунктом пересечения делятся пополам).
- Если в выпуклом четырёхугольнике средняя линия образует равные углы с диагоналями четырёхугольника, то диагонали равны.
- Длина средней линии четырёхугольника меньше полусуммы двух других сторон или равна ей, если эти стороны параллельны, и только в этом случае.
- Середины сторон произвольного четырёхугольника — вершины параллелограмма. Его площадь равна половине площади четырёхугольника, а его центр лежит на точке пересечения средних линий. Этот параллелограмм называется параллелограммом Вариньона;
- Последний пункт означает следующее: В выпуклом четырёхугольнике можно провести четыре средние линии второго рода. Средние линии второго рода – четыре отрезка внутри четырёхугольника, проходящие через середины его смежных сторон параллельно диагоналям. Четыре средние линии второго рода выпуклого четырёхугольника разрезают его на четыре треугольника и один центральный четырёхугольник. Этот центральный четырёхугольник является параллелограммом Вариньона.
- Точка пересечения средних линий четырёхугольника является их общей серединой и делит пополам отрезок, соединяющий середины диагоналей. Кроме того, она является центроидом вершин четырёхугольника.
- В произвольном четырёхугольнике вектор средней линии равен полусумме векторов оснований.
Средняя линия трапеции[править | править код]
Средняя линия трапеции — отрезок, соединяющий середины боковых сторон этой трапеции. Отрезок, соединяющий середины оснований трапеции, называют второй средней линией трапеции.
Она рассчитывается по формуле: , где AD и BC — основания трапеции.
Свойства[править | править код]
- средняя линия параллельна основаниям
- средняя линия равна полусумме оснований
- cредняя линия разбивает фигуру на две трапеции, площади которых соотносятся как [1]
См. также[править | править код]
- Теорема Вариньона (геометрия)
Примечания[править | править код]
Источник
Средние линии треугольника
Определение. Средней линией треугольника называют отрезок, соединяющий середины двух сторон треугольника (рис. 1).

Рис.1
На рисунке 1 средней линией является отрезок DE.
Утверждение 1. Средняя линия треугольника параллельна не пересекающейся с ней стороне треугольника и равна половине этой стороны.
Доказательство. Рассмотрим произвольный треугольник ABC и обозначим буквой D середину стороны AB (рис. 2). Проведем через точку D до пересечения с прямой BC прямую, параллельную прямой AC . Обозначим буквой E точку пересечения прямых DE и BC .

Рис.2
Поскольку AD = DB , а прямые AC и DE параллельны, то выполнены все условия теоремы Фалеса, и можно заключить, что выполнено равенство: CE = EB . Отсюда вытекает, что точка E является серединой стороны CB , а отрезок DE является средней линией треугольника.
Первую часть утверждения 1 мы доказали.
Для того, чтобы доказать вторую часть утверждения 1, заметим, что в любом треугольнике можно провести три средних линии – отрезки DE , EF и FD (рис.3).

Рис.3
Поскольку
DE | | FC , DF | | EC ,
то четырёхугольник DECF – параллелограммчетырёхугольник DECF – параллелограмм, следовательно, DE = FC .
Поскольку
DE | | AF , AD | | FE ,
то четырёхугольник DEFA – параллелограммчетырёхугольник DEFA – параллелограмм, следовательно, DE = AF .
Но поскольку AF = FC , то отсюда вытекает равенство
что и требуется доказать.
Доказательство утверждения 1 закончено.
Следствие.
- Три средних линии делят треугольник на 4 равных треугольника ADF , DBE , ECF , DEF (рис. 4).
- Каждый из четырёх треугольников ADF , DBE , ECF , DEF подобен треугольнику ABC с коэффициентом подобия 0,5.

Рис.4
Средняя линия трапеции
Напомним, что трапециейтрапецией называют четырёхугольник, у которого две стороны параллельны, а две другие – не параллельны.
Параллельные стороны трапеции называют основаниями, а непараллельные стороны – боковыми сторонами трапеции.
Отрезки, соединяющие противоположные вершины трапеции, называют диагоналями трапеции.
Определение. Средней линией трапеции называют отрезок, соединяющий середины боковых сторон трапеции (рис. 5).


Рис.5
На рисунке 5 средней линией трапеции является отрезок EF .
Утверждение 2. Средняя линия трапеции параллельна основаниям трапеции и равна половине суммы этих оснований.


Рис.6
Доказательство. Проведем через вершину B и середину боковой стороны F трапеции прямую линию (рис. 6). Обозначим точку пересечения прямых BF и AD буквой G . Рассмотрим треугольники BCF и FDG . У этих треугольников стороны CF и FD равны, поскольку точка F – середина стороны CD . Углы BCF и FDG равны, поскольку они являются внутренними накрест лежащими углами, образованными при пересечении параллельных прямых BC и AD с секущей CD . Углы BFC и DFG равны, поскольку они являются вертикальными. Тем самым выполнены все условия признака равенства треугольников «По стороне и прилежащим к ней углам», и можно заключить, что треугольники BCF и FDG равны. Из равенства треугольников BCF и FDG следует равенство отрезков BF и FG , откуда вытекает, что отрезок EF является средней линией треугольника ABG . Поэтому
что и требовалось доказать.
Задача 1. Доказать, что средняя линия трапеции делит пополам любой отрезок с концами на основаниях трапеции.


Рис.7
Решение. Пусть ABCD – трапеция, EF – её средняя линия, LM – указанный отрезок (рис.7). Поскольку AE = EB , то, в силу теоремы Фалеса, выполнено равенство: LN = NM , что и требовалось доказать.
Задача 2. Доказать, что отрезок, который диагонали трапеции высекают на средней линии трапеции, равен половине разности оснований трапеции.


Рис.8
Решение. Пусть ABCD – трапеция, EF – её средняя линия, KL – указанный отрезок (рис.8). В соответствии с задачей 1 можем заключить, что точка K – середина отрезка AC , а точка L – середина отрезка BD . Поэтому отрезок EK – средняя линия треугольника BAC , а отрезок EL – средняя линия треугольника ABD . В силу утверждения 1 выполнены равенства:
Следовательно,
что и требовалось доказать.
Утверждение 3. Прямая, проходящая через середины оснований трапеции, проходит через точку пересечения боковых сторон трапеции.

Рис.9
Доказательство. Пусть K и L – середины оснований BC и AD трапеции ABCD соответственно (рис.9). Обозначим буквой M точку пересечения боковых сторон AB и CD . Проведем через точки M и K прямую и обозначим точку пересечения этой прямой с основанием AD символом N . Докажем, что точки N и L совпадают. Для этого заметим, что треугольник BMK подобен треугольнику AMN . Следовательно, выполнено равенство:
Заметим также, что треугольник KMC подобен треугольнику NMD . Поэтому
Из этих соотношений получаем:
откуда вытекает, что точки N и L совпадают. Доказательство завершено.
Почти те же рассуждения позволяют доказать следующий факт, который мы предоставляем читателю в качестве упражнения.
Утверждение 4. Прямая, проходящая через точку пересечения диагоналей и середину одного из оснований трапеции, проходит через середину другого основания трапеции.
Следствие. Точка пересечения диагоналей, середины оснований и точка пересечения боковых сторон трапеции лежат на одной прямой.
Средние линии четырехугольника. Теорема Вариньона
Определение. Средней линией четырехугольника называют отрезок, соединяющий середины непересекающихся сторон четырёхугольника.
Поскольку у каждого четырехугольника имеются две пары непересекающихся сторон, то у каждого четырехугольника имеются две средних линии (рис.10).


Рис.10
На рисунке 10 средние линии – это отрезки EF и GH .
Замечание 1. Приведенное определение средней линии относится не только к плоским четырехугольникам, но и к «пространственным четырехугольникам» (рис.11). «Пространственным четырехугольником» мы называем замкнутую ломаную линию из 4 звеньев без самопересечений, не лежащую в одной плоскости.

Рис.11
На рисунке 11 изображен «пространственный четырёхугольник» ABCD , средними линиями которого являются отрезки EF и GH .
Замечание 2. Несмотря на то, что трапеция является четырехугольником, принято средней линией трапеции называть только отрезок, соединяющий середины её боковых сторон.
Замечание 3. В данном разделе справочника не рассматриваются невыпуклые четырёхугольники и четырёхугольники с самопересечениями.
Теорема Вариньона. Середины сторон произвольного плоского или «пространственного» четырёхугольника являются вершинами параллелограммапараллелограмма.
Доказательство. Рассмотрим плоский четырёхугольник ABCD , изображенный на рисунке 12. Точки E, G, F, H – середины сторон, отрезок AC – диагональ четырёхугольника.


Рис.12
Поскольку отрезок EG – средняя линия треугольника ABC , то отрезок EG параллелен диагонали AC и равен её половине. Поскольку отрезок FH – средняя линия треугольника CDA , то отрезок FH параллелен диагонали AC и равен её половине. Таким образом, в четырёхугольнике EGFH противоположные стороны EG и FH равны и параллельны. В силу признака параллелограммапризнака параллелограммапризнака параллелограмма отсюда вытекает, что четырёхугольник EGFH – параллелограмм, что и требовалось доказать.
Замечание 4 . В случае «пространственного четырёхугольника» ABCD доказательство остаётся тем же (рис. 13).

Рис.13
Поскольку диагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополамдиагонали параллелограмма в точке пересечения делятся пополам, то справедливо следующее утверждение, непосредственно вытекающее из теоремы Вариньона.
Утверждение 5. Средние линии произвольного четырёхугольника пересекаются и в точке пересечения делятся пополам (рис. 14).


Рис.14
Утверждение 6. Рассмотрим произвольный плоский или «пространственный» четырёхугольник ABCD , у которого отрезок EF является одной из средних линий (рис. 15). Тогда будет выполнено векторное равенство:

Рис.15
Доказательство. Рассмотрим в пространстве или на плоскости произвольную декартову систему координат с началом в некоторой точке O (рис. 16).


Рис.16
В соответствии со свойствами векторов справедливы следующие равенства:
что и требовалось доказать.
Следствие. Средняя линия четырёхугольника меньше или равна половине суммы не пересекающих её сторон четырёхугольника, причём равенство достигается лишь в том случае, когда указанные стороны четырёхугольника параллельны.
Другими словами, средняя линия четырёхугольника равна половине суммы не пересекающих её сторон четырёхугольника лишь в том случае, когда этот четырехугольник является трапециейтрапецией, а не пересекающие среднюю линию стороны четырёхугольника – основания трапеции.
Средние линии тетраэдра
Тетраэдром называют произвольную треугольную пирамиду (рис.17).

Рис.17
У каждого тетраэдра имеется 4 вершины, 4 грани и 6 рёбер, причем все рёбра делятся на 3 пары непересекающихся рёбер. На рисунке 17 каждая пара непересекающихся рёбер выделена отдельным цветом. Каждые два непересекающихся ребра тетраэдра лежат на скрещивающихся прямых скрещивающихся прямых.
Определение. Средней линией (бимедианой) тетраэдра называют отрезок, соединяющий середины двух непересекающихся рёбер тетраэдра.

Рис.18
У каждого тетраэдра имеется 3 средних линии. Изображённый на рисунке 18 отрезок EF является одной из средних линий тетраэдра.
Утверждение 7. Все средние линии тетраэдра пересекаются в одной точке и делятся этой точкой пополам.
Доказательство. Выберем какую-нибудь среднюю линию тетраэдра, например, EF и докажем, что любая другая средняя линия тетраэдра проходит через середину отрезка EF . Для этого рассмотрим, например, среднюю линию GH , соединяющую середины рёбер AC и BD , и соединим отрезками точки E, H, F, G (рис.19).

Рис.19
Заметим, что отрезок EH является средней линией треугольника ADB , поэтому
Отрезок GF является средней линией треугольника ACB , поэтому
Отсюда вытекает, что отрезки EH и GF равны и параллельны, следовательно, четырёхугольник EHFG – параллелограммследовательно, четырёхугольник EHFG – параллелограммследовательно, четырёхугольник EHFG – параллелограмм. Поскольку средние линии тетраэдра EF и GH являются диагоналями этого параллелограмма, то в точке пересечения они делятся пополамв точке пересечения они делятся пополамв точке пересечения они делятся пополам, что и требовалось доказать.
Определение. Точку пересечения средних линий тетраэдра называют центроидом тетраэдра.
Утверждение 8. Рассмотрим в пространстве декартову систему координат с началом в точке O и произвольный тетраэдр ABCD . Если обозначить буквой M центроид этого тетраэдра (рис. 20), то будет выполнено векторное равенство:


Рис.20
Доказательство. По свойствам векторов
что и требовалось доказать.
На сайте можно также ознакомиться с нашими учебными материалами для подготовки к ЕГЭ и ОГЭ по математике.
Источник
