Каким свойством обладает параллелограмм

Определение.
Параллелограмм – это четырехугольник у которого противоположные стороны попарно параллельны (лежат на параллельных прямых).
Параллелограммы отличаются между собой как размером прилегающих сторон, так и углами, однако противоположные углы одинаковые.
Признаки параллелограмма
Четырехугольник ABCD будет параллелограммом, если выполняется хотя бы одно из следующих условий:
1. Четырехугольник имеет две пары параллельных сторон:
AB||CD, BC||AD
2. Четырехугольник имеет пару параллельных и равных сторон:
AB||CD, AB = CD (или BC||AD, BC = AD)
3. В четырехугольнике противоположные стороны попарно равны:
AB = CD, BC = AD
4. В четырехугольнике противоположные углы попарно равны:
∠DAB = ∠BCD, ∠ABC = ∠CDA
5. В четырехугольнике диагонали точкой пересечения делятся пополам:
AO = OC, BO = OD
6. Сумма углов четырехугольника прилегающих к любой стороне равна 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
7. В четырехугольнике сумма квадратов диагоналей равна сумме квадратов его сторон:
AC2 + BD2 = AB2 + BC2 + CD2 + AD2
Основные свойства параллелограмма
Квадрат, прямоугольник и ромб – есть параллелограммом.
1. Противоположные стороны параллелограмма имеют одинаковую длину:
AB = CD, BC = AD
2. Противоположные стороны параллелограмма параллельны:
AB||CD, BC||AD
3. Противоположные углы параллелограмма одинаковые:
∠ABC = ∠CDA, ∠BCD = ∠DAB
4. Сумма углов параллелограмма равна 360°:
∠ABC + ∠BCD + ∠CDA + ∠DAB = 360°
5. Сумма углов параллелограмма прилегающих к любой стороне равна 180°:
∠ABC + ∠BCD = ∠BCD + ∠CDA = ∠CDA + ∠DAB = ∠DAB + ∠DAB = 180°
6. Каждая диагональ делит параллелограмма на два равных треугольника
7. Две диагональ делят параллелограмм на две пары равных треугольников
8. Диагонали параллелограмма пересекаются и точкой пересечения делят друг друга пополам:
| AO = CO = | d1 |
| 2 | |
| BO = DO = | d2 |
| 2 |
9. Точка пересечения диагоналей называется центром симметрии параллелограмма
10. Сумма квадратов диагоналей параллелограмма равна сумме квадратов его сторон:
AC2 + BD2 = 2AB2 + 2BC2
11. Биссектрисы противоположных углов параллелограмма всегда параллельны
12. Биссектрисы соседних углов параллелограмма всегда пересекаются под прямым углом (90°)
Стороны параллелограмма
Формулы определения длин сторон параллелограмма:
1. Формула сторон параллелограмма через диагонали и угол между ними:
a =
√d12 + d22 – 2d1d2·cosγ2 =
√d12 + d22 + 2d1d2·cosδ2
b =
√d12 + d22 + 2d1d2·cosγ2 =
√d12 + d22 – 2d1d2·cosδ2
2. Формула сторон параллелограмма через диагонали и другую сторону:
3. Формула сторон параллелограмма через высоту и синус угла:
4. Формула сторон параллелограмма через площадь и высоту:
Диагонали параллелограмма
Определение.
Диагональю параллелограмма называется любой отрезок соединяющий две вершины противоположных углов параллелограмма.
Параллелограмм имеет две диагонали – длинную d1, и короткую – d2
Формулы определения длины диагонали параллелограмма:
1. Формулы диагоналей параллелограмма через стороны и косинус угла β (по теореме косинусов)
d1 = √a2 + b2 – 2ab·cosβ
d2 = √a2 + b2 + 2ab·cosβ
2. Формулы диагоналей параллелограмма через стороны и косинус угла α (по теореме косинусов)
d1 = √a2 + b2 + 2ab·cosα
d2 = √a2 + b2 – 2ab·cosα
3. Формула диагонали параллелограмма через две стороны и известную другую диагональ:
d1 = √2a2 + 2b2 – d22
d2 = √2a2 + 2b2 – d12
4. Формула диагонали параллелограмма через площадь, известную диагональ и угол между диагоналями:
| d1 = | 2S | = | 2S |
| d2·sinγ | d2·sinδ |
| d2 = | 2S | = | 2S |
| d1·sinγ | d1·sinδ |
Периметр параллелограмма
Определение.
Периметром параллелограмма называется сумма длин всех сторон параллелограмма.
Формулы определения длины периметра параллелограмма:
1. Формула периметра параллелограмма через стороны параллелограмма:
P = 2a + 2b = 2(a + b)
2. Формула периметра параллелограмма через одну сторону и две диагонали:
P = 2a + √2d12 + 2d22 – 4a2
P = 2b + √2d12 + 2d22 – 4b2
3. Формула периметра параллелограмма через одну сторону, высоту и синус угла:
Площадь параллелограмма
Определение.
Площадью параллелограмма называется пространство ограниченный сторонами параллелограмма, т.е. в пределах периметра параллелограмма.
Формулы определения площади параллелограмма:
1. Формула площади параллелограмма через сторону и высоту, проведенную к этой стороне:
S = a · ha
S = b · hb
2. Формула площади параллелограмма через две стороны и синус угла между ними:
S = ab sinα
S = ab sinβ
3. Формула площади параллелограмма через две диагонали и синус угла между ними:
Источник
Определение
Параллелограмм – это четырехугольник, у которого противоположные стороны попарно параллельны.
Теорема (первый признак параллелограмма)
Если в четырехугольнике две стороны равны и параллельны, то этот четырехугольник – параллелограмм.
Доказательство
Пусть в четырехугольнике (ABCD) стороны (AB) и (CD) параллельны и (AB = CD).

Проведём диагональ (AC), разделяющую данный четырехугольник на два равных треугольника: (ABC) и (CDA). Эти треугольники равны по двум сторонам и углу между ними ((AC) – общая сторона, (AB = CD) по условию, (angle 1 = angle 2) как накрест лежащие углы при пересечении параллельных прямых (AB) и (CD) секущей (AC)), поэтому (angle 3 = angle 4). Но углы (3) и (4) накрест лежащие при пересечении прямых (AD) и (BC) секущей (AC), следовательно, (ADparallel BC). Таким образом, в четырехугольнике (ABCD) противоположные стороны попарно параллельны, и, значит, четырехугольник (ABCD) – параллелограмм.
Теорема (второй признак параллелограмма)
Если в четырехугольнике противоположные стороны попарно равны, то этот четырехугольник – параллелограмм.
Доказательство
Проведём диагональ (AC) данного четырехугольника (ABCD), разделяющую его на треугольники (ABC) и (CDA).

Эти треугольники равны по трем сторонам ((AC) – общая, (AB = CD) и (BC = DA) по условию), поэтому (angle 1 = angle 2) – накрест лежащие при (AB) и (CD) и секущей (AC). Отсюда следует, что (ABparallel CD). Так как (AB = CD) и (ABparallel CD), то по первому признаку параллелограмма четырёхугольник (ABCD) – параллелограмм.
Теорема (третий признак параллелограмма)
Если в четырехугольнике диагонали пересекаются и точкой пересечения делятся пополам, то этот четырехугольник – параллелограмм.
Доказательство
Рассмотрим четырехугольник (ABCD), в котором диагонали (AC) и (BD) пересекаются в точке (O) и делятся этой точкой пополам.
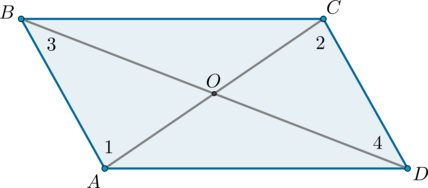
Треугольники (AOB) и (COD) равны по первому признаку равенства треугольников ((AO = OC), (BO = OD) по условию, (angle AOB = angle
COD) как вертикальные углы), поэтому (AB = CD) и (angle 1 = angle
2). Из равенства углов (1) и (2) (накрест лежащие при (AB) и (CD) и секущей (AC)) следует, что (ABparallel CD).
Итак, в четырехугольнике (ABCD) стороны (AB) и (CD) равны и параллельны, значит, по первому признаку параллелограмма четырехугольник (ABCD) – параллелограмм.
Свойства параллелограмма:
1. В параллелограмме противоположные стороны равны и противоположные углы равны.
2. Диагонали параллелограмма точкой пересечения делятся пополам.
Свойства биссектрисы параллелограмма:
1. Биссектриса параллелограмма отсекает от него равнобедренный треугольник.
2. Биссектрисы смежных углов параллелограмма пересекаются под прямым углом.
3. Отрезки биссектрис противоположных углов равны и параллельны.
Доказательство
1) Пусть (ABCD) – параллелограмм, (AE) – биссектриса угла (BAD).
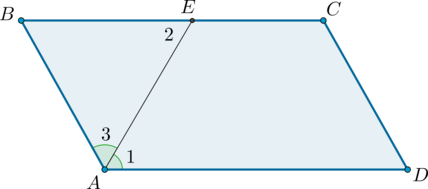
Углы (1) и (2) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (AE). Углы (1) и (3) равны, так как (AE) – биссектриса. В итоге (angle 3 = angle 1 = angle 2), откуда следует, что треугольник (ABE) – равнобедренный.
2) Пусть (ABCD) – параллелограмм, (AN) и (BM)– биссектрисы углов (BAD) и (ABC) соответственно.
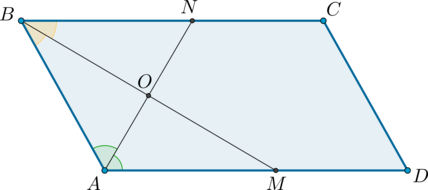
Так как сумма односторонних углов при параллельных прямых и секущей равна (180^{circ}), тогда (angle DAB + angle ABC =
180^{circ}).
Так как (AN) и (BM) – биссектрисы, то (angle BAN + angle ABM =
0,5(angle DAB + angle ABC) = 0,5cdot 180^circ = 90^{circ}), откуда (angle AOB = 180^circ – (angle BAN + angle ABM) =
90^circ).
3. Пусть (AN) и (CM) – биссектрисы углов параллелограмма (ABCD).
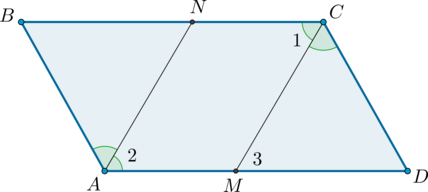
Так как в параллелограмме противоположные углы равны, то (angle 2 =
0,5cdotangle BAD = 0,5cdotangle BCD = angle 1). Кроме того, углы (1) и (3) равны как накрест лежащие при параллельных прямых (AD) и (BC) и секущей (CM), тогда (angle 2 = angle 3), откуда следует, что (ANparallel CM). Кроме того, (AMparallel CN), тогда (ANCM) – параллелограмм, следовательно, (AN = CM).
Источник
Параллелограмм — четырехугольник, у которого противоположные стороны попарно параллельны. Площадь параллелограмма равна произведению его основания (a) на высоту (h). Также можно найте его площадь через две стороны и угол и через диагонали.
Свойства параллелограмма
1. Противоположные стороны тождественны
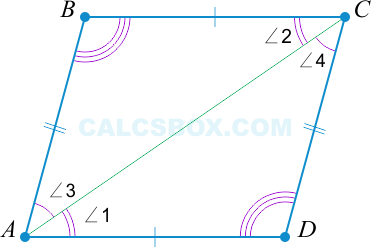
Первым делом проведем диагональ ( AC ). Получаются два треугольника: ( ABC ) и ( ADC ).
Так как ( ABCD ) — параллелограмм, то справедливо следующее:
( AD || BC Rightarrow angle 1 = angle 2 ) как лежащие накрест.
( AB || CD Rightarrow angle3 = angle 4 ) как лежащие накрест.
Следовательно, ( triangle ABC = triangle ADC ) (по второму признаку: ( angle 1 = angle 2, angle 3 = angle 4 ) и ( AC ) — общая).
И, значит, ( triangle ABC = triangle ADC ), то ( AB = CD ) и ( AD = BC ).
2. Противоположные углы тождественны
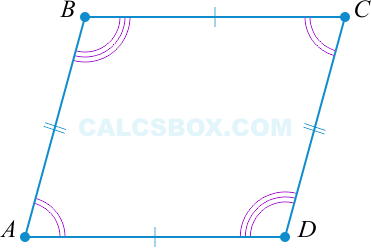
Согласно доказательству свойства 1 мы знаем, что ( angle 1 = angle 2, angle 3 = angle 4 ). Таким образом сумма противоположных углов равна: ( angle 1 + angle 3 = angle 2 + angle 4 ). Учитывая, что ( triangle ABC = triangle ADC ) получаем ( angle A = angle C ), ( angle B = angle D ).
3. Диагонали разделены пополам точкой пересечения
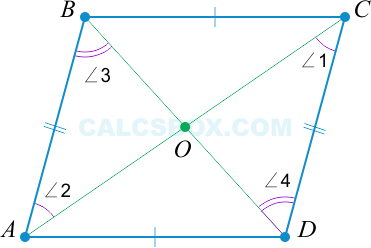
По свойству 1 мы знаем, что противоположные стороны тождественны: ( AB = CD ). Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что ( triangle AOB = triangle COD ) по второму признаку равенства треугольников (два угла и сторона между ними). То есть, ( BO = OD ) (напротив углов ( angle 2 ) и ( angle 1 )) и ( AO = OC ) (напротив углов ( angle 3 ) и ( angle 4 ) соответственно).
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны
( AB = CD ); ( AB || CD Rightarrow ABCD ) — параллелограмм.
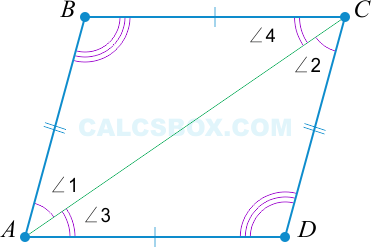
Рассмотрим подробнее. Почему ( AD || BC )?
( triangle ABC = triangle ADC ) по свойству 1: ( AB = CD ), ( angle 1 = angle 2 ) как накрест лежащие при параллельных ( AB ) и ( CD ) и секущей ( AC ).
Но если ( triangle ABC = triangle ADC ), то ( angle 3 = angle 4 ) (лежат напротив ( AD || BC ) (( angle 3 ) и ( angle 4 ) – накрест лежащие тоже равны).
Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны
( AB = CD ), ( AD = BC Rightarrow ABCD ) — параллелограмм.
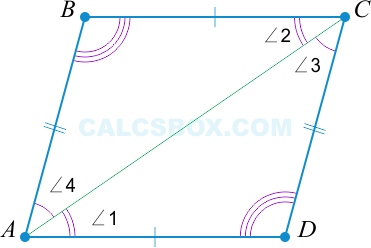
Рассмотрим данный признак. Еще раз проведем диагональ ( AC ).
По свойству 1 ( triangle ABC = triangle ACD ).
Из этого следует, что: ( angle 1 = angle 2 Rightarrow AD || BC ) и ( angle 3 = angle 4 Rightarrow AB || CD ), то есть ( ABCD ) — параллелограмм.
Второй признак верен.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны
( angle A = angle C ), ( angle B = angle D Rightarrow ABCD ) — параллелограмм.
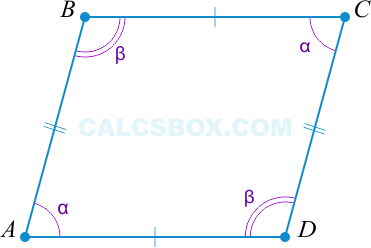
( 2 alpha + 2 beta = 360^{circ} ) (поскольку ( angle A = angle C ), ( angle B = angle D ) по условию).
Получается, ( alpha + beta = 180^{circ} ). Но ( alpha ) и ( beta ) являются внутренними односторонними при секущей ( AB ).
И то, что ( alpha + beta = 180^{circ} ) говорит и о том, что ( AD || BC ).
При этом ( alpha ) и ( beta ) — внутренние односторонние при секущей ( AB || CD ).
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам
( AO = OC ); ( BO = OD Rightarrow ) параллелограмм.
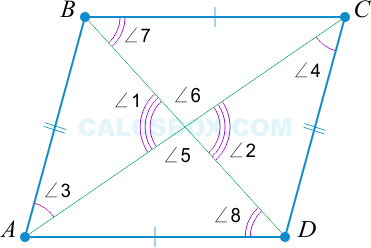
( BO = OD ); ( AO = OC ), ( angle 1 = angle 2 ) как вертикальные ( Rightarrow triangle AOB = triangle COD ), ( Rightarrow angle 3 = angle 4 ), и ( Rightarrow AB || CD ).
Аналогично ( BO = OD ); ( AO = OC ), ( angle 5 = angle 6 Rightarrow triangle AOD = triangle BOC Rightarrow angle 7 = angle 8 ), и ( Rightarrow AD || BC ).
Четвертый признак верен.
Источник
Если материал понравился Вам и оказался для Вас полезным, поделитесь им со своими друзьями!
Источник
Свойства параллелограмма
1. Противоположные стороны тождественны.

Доказательство
Первым делом проведем диагональ AC. Получаются два треугольника: ABC и ADC.

Так как ABCD — параллелограмм, то справедливо следующее:
AD || BC Rightarrow angle 1 = angle 2 как лежащие накрест.
AB || CD Rightarrow angle3 = angle 4 как лежащие накрест.
Следовательно, triangle ABC = triangle ADC (по второму признаку: angle 1 = angle 2, angle 3 = angle 4 и AC — общая).
И, значит, triangle ABC = triangle ADC, то AB = CD и AD = BC.
Доказано!
2. Противоположные углы тождественны.

Доказательство
Согласно доказательству свойства 1 мы знаем, что angle 1 = angle 2, angle 3 = angle 4. Таким образом сумма противоположных углов равна: angle 1 + angle 3 = angle 2 + angle 4. Учитывая, что triangle ABC = triangle ADC получаем angle A = angle C, angle B = angle D.
Доказано!
3. Диагонали разделены пополам точкой пересечения.

Доказательство
Проведем еще одну диагональ.

По свойству 1 мы знаем, что противоположные стороны тождественны: AB = CD. Еще раз отметим накрест лежащие равные углы.
Таким образом видно, что triangle AOB = triangle COD по второму признаку равенства треугольников (два угла и сторона между ними). То есть, BO = OD (напротив углов angle 2 и angle 1) и AO = OC (напротив углов angle 3 и angle 4 соответственно).

Доказано!
Признаки параллелограмма
Если лишь один признак в вашей задаче присутствует, то фигура является параллелограммом и можно использовать, все свойства данной фигуры.
Для лучшего запоминания, заметим, что признак параллелограмма будет отвечать на следующий вопрос — «как узнать?». То есть, как узнать, что заданная фигура это параллелограмм.
1. Параллелограммом является такой четырехугольник, у которого две стороны равны и параллельны.

AB = CD; AB || CD Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим подробнее. Почему AD || BC?

triangle ABC = triangle ADC по свойству 1: AB = CD, AC — общая и angle 1 = angle 2 как накрест лежащие при параллельных AB и CD и секущей AC.
Но если triangle ABC = triangle ADC, то angle 3 = angle 4 (лежат напротив AB и CD соответственно). И следовательно AD || BC (angle 3 и angle 4 – накрест лежащие тоже равны).

Первый признак верен.
2. Параллелограммом является такой четырехугольник, у которого противоположные стороны равны.

AB = CD, AD = BC Rightarrow ABCD — параллелограмм.
Доказательство
Рассмотрим данный признак. Еще раз проведем диагональ AC.

По свойству 1 triangle ABC = triangle ACD.

Из этого следует, что: angle 1 = angle 2 Rightarrow AD || BC и angle 3 = angle 4 Rightarrow AB || CD, то есть ABCD — параллелограмм.
Второй признак верен.
3. Параллелограммом является такой четырехугольник, у которого противоположные углы равны.

angle A = angle C, angle B = angle D Rightarrow ABCD — параллелограмм.
Доказательство

2 alpha + 2 beta = 360^{circ} (поскольку ABCD — четырехугольник, а angle A = angle C, angle B = angle D по условию).
Получается, alpha + beta = 180^{circ}. Но alpha и beta являются внутренними односторонними при секущей AB.
И то, что alpha + beta = 180^{circ} говорит и о том, что AD || BC.
При этом alpha и beta — внутренние односторонние при секущей AD. И это значит AB || CD.
Третий признак верен.
4. Параллелограммом является такой четырехугольник, у которого диагонали разделены точкой пересечения пополам.

AO = OC; BO = OD Rightarrow параллелограмм.
Доказательство

BO = OD; AO = OC, angle 1 = angle 2 как вертикальные Rightarrow triangle AOB = triangle COD, Rightarrow angle 3 = angle 4, и Rightarrow AB || CD.
Аналогично BO = OD; AO = OC, angle 5 = angle 6 Rightarrow triangle AOD = triangle BOC Rightarrow angle 7 = angle 8, и Rightarrow AD || BC.
Четвертый признак верен.
Источник
Ñâîéñòâà ñòîðîí è óãëîâ ïàðàëëåëîãðàììà.
Ó ïàðàëëåëîãðàììà ïðîòèâîïîëîæíûå ñòîðîíû èìåþò îäèíàêîâóþ äëèíó, à ïðîòèâîïîëîæíûå óãëû ðàâíóþ âåëè÷èíó.

Äàíî:
ABCD — ïàðàëëåëîãðàìì.
Äîêàçàòü:
AB=CD, AD=BC,
∠A=∠C, ∠B=∠D.
Äîêàçàòåëüñòâî:
Ïðîâîäèì â ïàðàëëåëîãðàììå ABCD äèàãîíàëü BD.

Ðàññìàòðèâàåì òðåóãîëüíèêè ABD è CDB. Çäåñü âàæíî ïðàâèëüíî óêàçàòü òðåóãîëüíèêè.
1) Ñòîðîíà BD ÿâëÿåòñÿ îáùåé.
2) ∠ABD=∠CDB (êàê âíóòðåííèå íàêðåñò ëåæàùèå ïðè AB∥CD è ñåêóùåé BD)
3) ∠ADB=∠CBD (êàê âíóòðåííèå íàêðåñò ëåæàùèå ïðè AD∥BC è ñåêóùåé BD)
Òî åñòü, ∆ABD= ∆CDB (ïî ñòîðîíå è 2-ì ïðèëåæàùèì ê íåé óãëàì).
Èç ðàâåíñòâà òðåóãîëüíèêîâ ñëåäóåò ðàâåíñòâî ñîîòâåòñòâóþùèõ ñòîðîí:
AB=CD, AD=BC
è ðàâåíñòâî ñîîòâåòñòâóþùèõ óãëîâ:
∠A=∠C.
 ïóíêòàõ 2) è 3) îáúÿñíåíî, ÷òî ∠ABD=∠CDB è ∠ADB=∠CB.
Çíà÷èò,
∠ABC=∠ABD+∠CBD=∠CDB+∠ADB=∠ADC,
Ò.å., ∠B=∠D. ×òî è òðåáîâàëîñü äîêàçàòü.
Ñâîéñòâî óãëîâ ïàðàëëåëîãðàììà, ïðèëåæàùèõ ê îäíîé ñòîðîíå.
Ñóììà óãëîâ ïàðàëëåëîãðàììà, êîòîðûå ïðèëåæàò ê îäíîé ñòîðîíå ñîîòâåòñòâóåò 180 ãðàäóñàì.
Ýòî ñâîéñòâî âûõîäèò èç òîãî, ÷òî óãëû, êîòîðûå ïðèëåæàò ê 1-îé ñòîðîíå ïàðàëëåëîãðàììà îêàçûâàþòñÿ âíóòðåííèìè îäíîñòîðîííèìè óãëàìè ïðè ïàðàëëåëüíûõ ïðÿìûõ.
Äëÿ ïàðàëëåëîãðàììà ABCD:
∠A+∠B=180º (êàê âíóòðåííèå îäíîñòîðîííèå ïðè AD∥BC è ñåêóùåé AB;
∠C+∠D=180º (êàê âíóòðåííèå îäíîñòîðîííèå ïðè AD∥BC è ñåêóùåé CD;
∠A+∠D=180º (êàê âíóòðåííèå îäíîñòîðîííèå ïðè AB∥CD è ñåêóùåé AD;
∠B+∠C=180º (êàê âíóòðåííèå îäíîñòîðîííèå ïðè AB∥CD è ñåêóùåé BC.
Åùå íåêîòîðûå ñâîéñòâà óãëîâ ïàðàëëåëîãðàììà:
Áèññåêòðèñû óãëîâ ïàðàëëåëîãðàììà, êîòîðûå ïðèëåæàò ê îäíîé ñòîðîíå, — ïåðïåíäèêóëÿðíû.
Áèññåêòðèñû ïðîòèâîëåæàùèõ óãëîâ ïàðàëëåëîãðàììà — ïàðàëëåëüíû.
Áèññåêòðèñà óãëà ïàðàëëåëîãðàììà îòñåêàåò îò íåãî ðàâíîáåäðåííûé òðåóãîëüíèê.
Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
| Ïîìîùü â ðåøåíèè çàäà÷ ïî ãåîìåòðèè, ó÷åáíèê îíëàéí (âñå êàëüêóëÿòîðû ïî ãåîìåòðèè). | |
| Êàëüêóëÿòîðû ïî ãåîìåòðèè | |
Ãåîìåòðè÷åñêèå ôèãóðû. | |
| Ãåîìåòðè÷åñêèå ôèãóðû – ïèðàìèäà, ïðÿìîóãîëüíèê, ðîìá, óãëû, øàð, ïàðàëëåëîãðàìì, ïàðàëëåëåïèïåä, ïðèçìà, ñâîéñòâà, ôîðìóëû ãåîìåòðè÷åñêèõ ôèãóð | |
| Ãåîìåòðè÷åñêèå ôèãóðû. | |
Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
| Îñíîâíàÿ èíôîðìàöèÿ ïî êóðñó ãåîìåòðèè äëÿ îáó÷åíèÿ è ïîäãîòîâêè â ýêçàìåíàì, ÃÂÝ, ÅÃÝ, ÎÃÝ, ÃÈÀ | |
| Ãåîìåòðèÿ 6,7,8,9,10,11 êëàññ, ÅÃÝ, ÃÈÀ | |
Ãåîìåòðè÷åñêèå ôèãóðû. Ïðàâèëüíàÿ ïèðàìèäà. | |
| Ïðàâèëüíàÿ ïèðàìèäà – êîãäà îñíîâàíèåì ïèðàìèäû ÿâëÿåòñÿ ïðàâèëüíûé ìíîãîóãîëüíèê, à âûñîòà ïðîåöèðóåòñÿ â öåíòð îñíîâàíèÿ (èëè ïðîõîäèò ÷åðåç íåãî). | |
| Ãåîìåòðè÷åñêèå ôèãóðû. Ïðàâèëüíàÿ ïèðàìèäà. | |
Ãåîìåòðè÷åñêèå ôèãóðû. Ïðèçìà. Îáúåì ïðèçìû. | |
| Ïðèçìà ìíîãîãðàííèê, 2 ãðàíè ýòî êîíãðóýíòíûå (ðàâíûå) ìíîãîóãîëüíèêè, êîòîðûå ëåæàò â ïàðàëëåëüíûõ ïëîñêîñòÿõ, à îñòàâøèåñÿ ãðàíè ïàðàëëåëîãðàììû, èìåþùèå îáùèå ñòîðîíû ñ ýòèìè ìíîãîóãîëüíèêàìè. | |
| Ãåîìåòðè÷åñêèå ôèãóðû. Ïðèçìà. Îáúåì ïðèçìû. | |
Источник
