Каким свойством обладает объем фигуры

Геометрия, 11 класс

Урок №11

Понятие объёма

Перечень вопросов, рассматриваемых на уроке:

Понятие объёма.

Свойства объёмов.

Объём прямоугольного параллелепипеда.

Формула объёма прямоугольного параллелепипеда.

Тезаурус

Объём тела– величина, характеризующая часть пространства, занимаемую телом, и определяемая формой и линейными размерами этого тела.

Основные свойства объёма:

– равные тела имеют равные объёмы;

– если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Основная литература:

Атанасян Л. С. и др. Математика: алгебра и начала математического анализа, геометрия. Геометрия. 10–11 классы [текст]: учеб. для общеобразоват. организаций: базовый и углубл. уровни – М.: Просвещение, 2014. – 255 с. С. 130–133.

Теоретический материал для самостоятельного изучения

С понятием объёмного тела, отличающегося от плоской фигуры, мы познакомились ещё в начальной школе.

Объёмом принято называть положительную величину, характеризующую часть пространства, занимаемую телом, и определяемую формой и линейными размерами этого тела.

Мы можем вычислить объём тела точно так же, как ранее находили площадь фигуры. Объём принято измерять в единицах измерения объёма (единицах измерения размера пространства, занимаемого телом), то есть в кубических метрах, сантиметрах, миллиметрах и так далее. За единицу измерения объёма можно принять куб с ребром 1 см, то есть, кубический сантиметр (обозначение: см3). По аналогии, можно за единицу измерения объёма принять кубический миллиметр (1 мм3), кубический метр (1 м3) и тому подобное.

Объём выражается в положительных числах. Это число показывает, сколько единиц измерения содержится в теле. Например, сколько кубических миллиметров в аквариуме, сколько кубических метровв бассейне и так далее.

Объём обозначается заглавной латинской буквой V.

Пример:

Объём книги400 кубических сантиметров запишут: V = 400см3.

Рассмотрим свойства объёмов.

Свойство № 1. Равные тела имеют равные объёмы. Это означает, что если два тела идентичны, то есть имеют равное количество единиц измерения и частей, то равны и их объёмы. Например, 2 одинаковых пакета молока равны в объёме.

Свойство № 2. Если тело составлено из нескольких тел, то его объём равен сумме объёмов этих тел.

Следствие из основных свойств объёмов.

Объём куба с ребром 1/n равен 1/n3

Доказательство. Рассмотрим куб, объём которого принят за единицу измерения объёмов, тоесть равный некоторому числукубических сантиметров. Его ребро равно единице измерения отрезков. Разобьём каждое ребро этого куба на произвольное количество частей – nтак, чтобы провести плоскости, перпендикулярные к этому ребру.

По второму свойству объёмов, сумма объёмов всех кубиков равна объёму всего куба (1 см3). Следовательно, поскольку мы разбили каждое ребро на n частей, то каждый маленький куб внутри большого куба будет иметь ребро

Объём каждого из маленьких кубиков при этом будет равен 1/n3.

Объём прямоугольного параллелепипеда

Теорема

Объём прямоугольного параллелепипеда равен произведению трёх его измерений.

Доказательство

Обозначимизмеренияпрямоугольного параллелепипеда P буквами a,b,c, его объём буквой V, и докажем, что V = a ∙ b ∙ c.

Рассмотрим два возможных случая.

Случай первый. Измерения a, b и c представляют собой конечные десятичные дроби, у которых число знаков после запятой не превосходит n (можно считать, что n больше или равно 1). В этом случае числа a ∙10n, b∙10n, c∙10n, являются целыми. Разобьём каждое ребро параллелепипеда на равные части длины: 1/10n и через точки разбиения проведём плоскости, перпендикулярные к этому ребру. Параллелепипед P разобьётся на abc∙103n равных кубов с ребром 1/10n. Так как объём каждого куба равен 1/103n, что мы доказали ранее, то объём всего параллелепипеда P = abc, что и требовалось доказать.

Случай второй.

Хотя бы одно из измерений a, b, c представляет собой бесконечную десятичную дробь. Рассмотрим конечные десятичные дроби: an, bn, cn, которые получаются из чисел a, b, c, если отбросить в каждом из них все цифры после запятой, начиная с n + 1. Очевидно, an ≤ a ≤ an’, где an’ = an+1 : 10n. Аналогичные неравенства справедливы для b и c. Перемножив эти неравенства, получим произведение anbncn ≤ abc ≤ an’bn’cn’, где bn’= bn+1 : 10n, cn’ = cn+1 : 10n

По доказанному в первом случае, левая часть неравенства представляет собой объём Vn прямоугольного параллелепипеда Pn с измерениями an, bn, cn, а правая часть – это объём Vn’ прямоугольного параллелепипеда Pn’ с измерениями an’, bn’, cn’. Так как параллелепипед P содержит в себе параллелепипед Pn, а сам содержится в параллелепипеде Pn’, то объём V параллелепипеда P заключён между Vn, = anbncn и Vn’= an’bn’cn’. Будем неограниченно увеличивать n. Тогда 1/10n будет становиться сколь угодно малым, и поэтому произведение an’bn’cn’ будет сколь угодно мало отличаться от числа, выраженного произведением anbncn. Отсюда следует, что число V сколь угодно мало отличается от числа, выраженного произведением anbncn, а значит, они равны.V = abc, что и требовалось доказать.

Примеры и разбор решения заданий тренировочного модуля.

№1.Длины сторон основания прямоугольного параллелепипеда равны 15 см и 20 см. Высота параллелепипеда равна диагонали основания. Найдите объём этого параллелепипеда.

Решение:

Найдём длину диагонали основания, для этого воспользуемся теоремой Пифагора:

А теперь найдём объём параллелепипеда:

V = 15 ∙ 20 ∙ 25 = 7500 см3

Ответ: V = 7500 см3.

№2.

Найдите площадь закрашенной фигуры, если объём прямоугольного параллелепипеда равен 960 см3, AB = 8 см, АА1= 20 см.

Варианты ответов:

220 см2

100 см2

400 см2

200 см2

Решение.

Найдём длину АD:

AD = 960 : 8 : 20 = 6 см

Найдём АС, воспользовавшись теоремой Пифагора:

Закрашенная фигура – прямоугольник. Вычислим его площадь: 10∙20= 200 см2.

Ответ: площадь закрашенной фигуры 200 см2.

Верный ответ: 200 см2.

Нетрадиционная форма урока.

Понятие объема и его свойств вводилось по аналогии, в сравнении с понятием
площади многоугольника на плоскости (проверялись остаточные знания по данной
теме в форме устного опроса).

Понятие объема прямоугольного параллелепипеда и объем куба были записаны с
помощью ответов учащихся (ранее изученные темы).

Остальные формулы объемов тел были выведены поэтапно, применяя ранее знакомые
понятия и формулы, в процессе фронтальной беседы с учащимися.

Закрепление нового материала отрабатывалось на решении как полуустных задач,
так и на письменных задачах. Образцы правильного решения и оформления задач были
продемонстрированы на слайдах.

Кроме этого были показаны примеры использования понятий стереометрии в других
науках: физике, биологии, географии и др.

Во время проведения урока чувствовался неподдельный интерес учащихся, о чем
они написали после урока в своих отзывах. Во время данного урока был охвачен
большой объем теоретического материала на наглядном и доступном уровне, с
экономией 5 уроков, которые будут использованы для решения задач по данной теме.

В конце урока проведена рефлексия с учащимися класса.

Уровень дисциплины хороший. Очень активны на уроке около 80% учащихся;
остальные усваивают материал на индивидуальном уровне.

Усвоение знаний осуществляется через применение ТСО, самостоятельную работу,
индивидуальную и фронтальную работу учащихся.

На уроке используются методы: объяснительно-иллюстративный, репродуктивный,
проблемное изложение, частично– поисковый.

Применяются приемы: аналогия, сравнение, анализ; устное решение задач;
повторение формул; применение формул в новых условиях; беседа; формулирование
выводов самими учащимися; слайдовые решения и оформление задач для самопроверки;
решение задач по алгоритму.

Темп урока средний, что соответствует познавательным способностям учащихся и
уровню их работоспособности.

В ходе урока обращается внимание на уровень дисциплины, степень усвоения
материала, выполнение плана урока; оценивают и комментируют ответы учащихся; при
необходимости корректируют знания учащихся.

На уроке применяются пособия: слайдовые, наглядно-иллюстративные изображения
растений ит.д. Дифференциация осуществлялась через наводящие вопросы, , через
алгоритм решения задач.

Оригинальность заданий проявилась в том, что учащиеся узнавали новые знания
на основе имеющихся знаний, приводили примеры из жизни (то есть практико-ориентированные задания).

На уроке применялись, в основном, репродуктивные методы, так как это связано
с психологическими особенностями учащихся. Творчество учащихся проявилось в
интеграции; учащиеся применяли свои знания математики в литературе, биологии,
географии.

Психологическая атмосфера на уроке спокойная, доброжелательная, деловая.
Общение учителей с учащимися корректное.

Выводы:

1. Цели и задачи урока выполнены.
2. Урок нетрадиционный, интересный, продуктивный.
3. Материал повторен каждым учащимся на своем индивидуальном уровне
   благодаря наглядности, доступности, разнообразию приемов и методов.
4. Подобная нетрадиционная форма урока позволила сэкономить время для
   отработки полученных знаний при решении задач.

Цели и задачи урока:

1. ввести понятие объема тел его свойств, единиц измерения объема,
   познакомить с объемами параллелепипеда, куба, прямой призмы, пирамиды,
   цилиндра и конуса, руководствуясь наглядно-иллюстративными соображениями;
2. учить сравнивать, сопоставлять, анализировать, делать выводы, развивать
   правильную математическую речь, целесообразную вариативности математических
   упражнений, закрепить знания в результате решения задач на применение новых
   формул объема;
3. воспитывать трудолюбие, внимательность; развитие интереса учащихся к
   предмету математика, активизация мыслительной деятельности, развитие
   математической речи, расширение математического кругозора у учащихся,
   научить учащихся мыслить логически, быстро думать и принимать правильные
   решения;

Педагогические возможности:

• повышение уровня математического мышления,
• углубление теоретических знаний,
• расширение кругозора,
• возникновение интереса к математике,
• воспитание стремления к совершенствованию своих знаний,
• формирование умений коллективного поиска ответов на вопросы,
• сплочение коллектива, формирование дружеских, товарищеских отношений

Использовалась дополнительная литература:

• Все рисунки и чертежи выполнены автором данной работы – Варенко Оксаной
  Валентиновной в программах: Microsoft
  Office
  Word, Paint.
• В данной работе использованы фотографии c
  сайтов:
  –
  ru.wikipedia.org›wiki/Конус_выноса
  
  images.yandex.ru›конуснарастания
  
  medusy.ru›diving/yad_mollusk/index.shtm
  
  reinesland.ru›wiki/Телесный_угол

Ход урока

Приложение. Слайд 1 и Слайд 2.

Учитель: Сегодня на
уроке мы с вами введем понятие объема тел его свойств, познакомимся и узнаем
единицы измерения объема, познакомимся с объемами параллелепипеда, куба, прямой
призмы, пирамиды, цилиндра и конуса, руководствуясь наглядно-иллюстративными
соображениями.

Слайд 3.

Подобно тому как все искусства тяготеют к музыке, все науки стремятся к
математике.
Д. Сантаяна

Слайд 4.

Геометрия есть искусство правильно рассуждать на неправильных чертежах.
Пойа Д.

Повторение с частичным (первичным) введением нового материала. (Повторить
известные многогранники и тела вращения– определения и чертежи – заранее
заготовленных карточках.)

Найдите соответствия

Слайд 5: Изучение нового материала в сравнении – “Планиметрия–
Стереометрия”.

Понятие объема тела вводится по аналогии с понятием площади плоской фигуры.
Из курса планиметрии известно, что каждый многоугольник имеет площадь, которая
измеряется с помощью выбранной единицы измерения площадей. В качестве единицы
измерения площадей обычно берут квадрат, сторона которого равна единице
измерения отрезков.

Площадь многоугольника – это положительная величина той части плоскости ,
которую занимает многоугольник.

Аналогично будем считать, что каждое из рассматриваемых нами тел имеет объем,
который можно измерять с помощью выбранной единицы измерения объемов.

Объем тела – это положительная величина той части пространства , которую
занимает геометрическое тело.

Слайд 6: В чем измеряется площадь плоских фигур?

Какие единицы измерения площадей вы уже знаете?

За единицу измерения площадей берут квадрат, сторона которого равна единице
измерения отрезков.

1 км2, 1 м2, 1 дм2, 1 см2, 1 мм2
, 1 а, 1 га и т.д.

За единицу измерения объемов примем куб, ребро которого равно единице
измерения отрезков.

Куб с ребром 1 см называют кубическим сантиметром и обозначают см3.

Аналогично определяют :

1 м3, 1 дм3, 1 см3 , 1 мм3 и т.д.

Процедура измерения объемов тел аналогична процедуре измерения площадей. При
выбранной единице измерения объем каждого тела выражается положительным числом,
которое показывает . сколько единиц измерения объемов и частей единицы
содержится в данном теле.

Слайд 7.Мы с вами уже знакомы из курса планиметрии со
свойствами площадей.

Давайте вспомним первое свойство: (ученики используют подсказку на
слайде).

Равные многоугольники имеют равные площади.

Мы с вами можем сформулировать первое свойство объема тел используя в
качестве подсказки рисунок слайда. Равные тела имеют равные объемы.

Равенство двух фигур, в частности двух тел, в стереометрии определяется так
же, как и в планиметрии: два тела называются равными, если их можно совместить
наложением.

Слайд 8. Рассмотрим еще одно свойство объемов.

Для этого мы вспомним второе свойство из курса планиметрии: (ученики
используют подсказку на слайде). Свойство 2: – Если многоугольник
составлен из нескольких многоугольников, то его площадь равна сумме площадей
этих многоугольников.

SF=
SF1+
SF2+
SF3 +
SF4

Итак давайте выведем второе свойство объема: Если тело составлено из
нескольких тел, то его объем равен сумме объемов этих тел.

VF=
VF1+
VF2

Слайд 9. Мы с вами вспомнило некоторые свойства из курса планиметрии и
рассмотрели 2 свойства объемов.

Сформулируйте – какие фигуры называются равновеликими? Равновеликими
называются геометрические фигуры, имеющие равные площади
SF= SF1
.

Сформулируйте – какие тела называются равновеликими?
Равновеликими называются тела, объемы которых равны
VF=
VF1

Слайд 10. В стереометрии мы с вами будем рассматривать объемы
многогранников и объемы тел вращения

Назовите известные вам многогранники и фигуры вращения?

(Учащиеся должны
назвать – прямоугольный параллелепипед, куб, призма, пирамида, цилиндр, конус,
сфера и шар.)

Слайд 11. Введение формул объемов тел через диалог учителей и
учащихся.

В курсе математики 5-го класса мы с вами уже познакомились с прямоугольным
параллелепипедом. Давайте воспользуемся чертежом и вспомним основные элементы
прямоугольного параллелепипеда и формулы уже известные нам.

Измерения – а – длина; b –
ширина; с – высота.

Известные формулы:

V = a.b.c

Sосн =
a.b
V = Sосн.H

Следствие 1: Объем прямоугольного параллелепипеда равен произведению площади
основания на высоту.

Слайд 12. А как называется прямоугольный параллелепипед у которого все
измерения равны? Куб.

Длина куба а = а; ширина в = а; высота с = а.

Подставим имеющиеся данные в формулу V=a.b.c
в результате чего мы получаем:

(Ученики сами выводят формулу нахождения объема куба.)

V =
a.а.а = а3

V = а3

Слайд 13:

А сейчас мы рассмотрим прямую призму, основанием которой является
прямоугольный треугольник (используем рисунок на слайде).

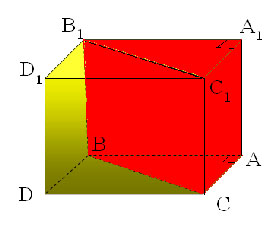
Ученики вспоминают, что прямая призма, основанием которой
является прямоугольный треугольник образуется путем разрезания прямоугольного
параллелепипеда на две равные части. Они могут самостоятельно определить формулу
для нахождения объема прямой призмы

Следствие 2 – Объем прямой призмы, основанием которой является прямоугольный
треугольник, равен произведению основания на высоту.

Слайд 14. А сейчас мы с вами найдем объем пирамиды. Достроим
пирамиду ABCS до призмы.
Достроенная призма будет состоять из 3 пирамид– SABC,
SCC1B1,
SCBB1. У 2 и 3
пирамиды– SC– общая, треугольник
CC1B1=
треугольнику CBB1

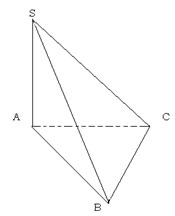
У 1 и 3 пирамиды – СS – общая,
треугольник SAB = треугольнику
BB1S

V1=V2=V3

V призмы= 3 V
пирам

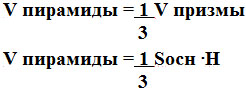
Слайд 15. Мы с вами узнали и вывели несколько формул для нахождения
объемов тел. А сейчас поработаем с телами вращения.

 Какие тела вращения вы уже знаете? Цилиндр. Конус, усеченный конус, сфера
и шар.

Давайте выведем с вами формулу для нахождения объема цилиндра.

Вспомним обозначения и уже известные нам формулы, которые мы применяли для
нахождения элементов цилиндра.

Обозначения:

R – радиус основания.
H – высота.
L – образующая.
L= H

V – объем цилиндра.

Sосн = ПR2

Говорят, что призма вписана в цилиндр, если ее основания вписаны в основания
цилиндра и призма описана около цилиндра, если ее основания описаны около
оснований цилиндра. Ясно, что высота любой призмы, вписанной в цилиндр или
описанной около него равна высоте самого цилиндра.

Теорема: Объем цилиндра равен произведению площади основания на высоту.

V = ПR2H

V = Sосн
.H

Слайд 16. Назовите мне фигуру вращения, которую вы видите на данном
слайде? Конус.

Давайте вспомним основные обозначения конуса и все уже известные нам формулы,
которые мы применяем при решении задач на нахождение элементов конуса.

Обозначения:

R – радиус основания.
L – образующая конуса.
H – высота.
V – объем.

Пирамида вписана в конус, если ее основания вписаны в основания конуса и
пирамида описана около конуса, если ее основания описаны около оснований конуса.
Ясно, что высота любой пирамиды, вписанной в конус или описанной около него
равна высоте самого конуса. Так как мы уже знаем с вами , что объем пирамиды
равен:  V пирамиды =
Sосн
.H
Тогда и Vконуса =
Sосн .H
, а в основании конуса лежит круг, то Sосн
= ПR2Н

Поэтому V=
ПR2Н

Слайд 17. Это интересно: (межпредметные
связи).

Слайд 18.

Проверь свои знания:

• Сформулируйте понятие объема.
• Сформулируйте основные свойства объемов тел.
• Назовите единицы измерения объема тел.
• Назовите формулу для измерения объема:
  – прямоугольного параллелепипеда;
  – объема куба;
  – объем прямой призмы;
  – объем пирамиды;
  – объем цилиндра
  – объем конуса.
• Изменится ли объем цилиндра, если радиус его осн