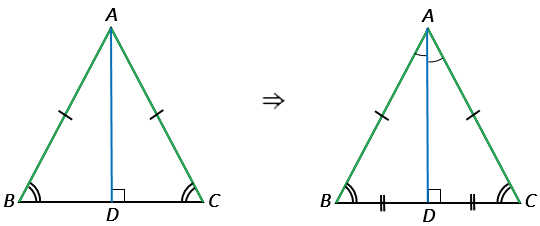
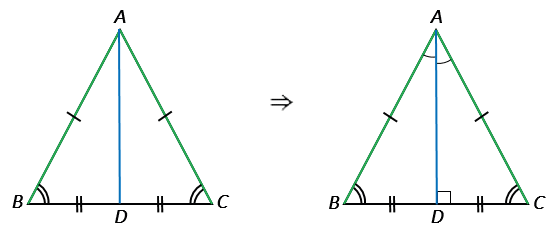
Каким свойством обладает медиана равнобедренного треугольника

Содержание:
- Свойства равнобедренного треугольника.
- Признаки равнобедренного треугольника.
- Формулы равнобедренного треугольника:
- формулы длины стороны;
- формулы длины равных сторон;
- формулы высоты, медианы, биссектрисы равнобедренного треугольника.
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.
АВ = ВС — боковые стороны
АС — основание
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника выражаются через 5 теорем:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Рассмотрим равнобедренный Δ ABC с основанием АС.
Боковые стороны равны АВ = ВС,
Следовательно углы при основании ∠ BАC = ∠ BСA.
Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника
- Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
- Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Доказательство теоремы:
- Дан Δ ABC.
- Из точки В проведем высоту BD.
- Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).
- Прямые АС и BD называются перпендикуляром.
- В Δ ABD и Δ BCD ∠ BАD = ∠ BСD (из Теоремы 1).
- АВ = ВС — боковые стороны равны.
- Стороны АD = СD, т.к. точка D отрезок делит пополам.
- Следовательно Δ ABD = ΔBCD.
- Биссектриса, высота и медиана это один отрезок – BD
Вывод:
- Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
- Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
- Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.
Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.
- Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство теоремы:
Дано два Δ ABC и Δ A1B1C1. Стороны AB = A1B1; BC = B1C1; AC = A1C1.
Доказательство от противного.
- Пусть треугольники не равны (а то треугольники были равны по первому признаку).
- Пусть Δ A1B1C2 = Δ ABC, у которого вершина C2 лежит в одной полуплоскости с вершиной C1 относительно прямой A1B1. По предположению вершины C1 и C2 не совпадают. Пусть D – середина отрезка C1C2. Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.
- Отсюда пришли к противоречию и теорему доказали.
Признаки равнобедренного треугольника
- Если в треугольнике два угла равны.
- Сумма углов треугольника 180°.
- Если в треугольнике биссектриса является медианой или высотой.
- Если в треугольнике медиана является биссектрисой или высотой.
- Если в треугольнике высота является медианой или биссектрисой.
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы длины стороны (основания — b):
- b = 2a sin( beta /2)= a sqrt { 2-2 cos beta }
- b = 2a cos alpha
Формулы длины равных сторон — (а):
- a=frac { b } { 2 sin(beta /2) } = frac { b } { sqrt { 2-2 cos beta } }
- a=frac { b } { 2 cosalpha }
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
- L — высота=биссектриса=медиана
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
- L = a sina
- L = frac { b } { 2 } *tgalpha
- L = a sqrt { (1 + cos beta)/2 } =a cos (beta)/2)
Формула высоты, биссектрисы и медианы, через стороны, (L):
- L = sqrt { a^ { 2 } -b^ { 2 } /4 }
Площадь равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- h — высота
Формула площади треугольника через высоту h и основание b, (S):
S=frac { 1 } { 2 } *bh
Смотри также:
- Теорема о сумме углов треугольника
- Формулы площади поверхности, основания, сечения призмы
- Площадь поверхности куба, формулы и примеры
- Основные формулы по математике
- Справочные материалы ЕГЭ от ФИПИ по математике
Источник
У этого термина существуют и другие значения, см. Медиана.
Треугольник и его медианы.
Медиа́на треуго́льника (лат. mediāna — средняя) ― отрезок, соединяющий вершину треугольника с серединой противоположной стороны. Иногда медианой называют также прямую, содержащую этот отрезок. Точка пересечения медианы со стороной треугольника называется основанием медианы.
Связанные определения[править | править код]
Три медианы, проходящие через общую точку
На рис. справа в треугольнике ABC через точку O проведены 3 медианы: AD, BE и CF. Тогда точка O пересечения 3 медиан разбивает каждую медиану на 2 отрезка прямых, один из них (который начинается в вершине, а заканчивается в точке пересечения O) мы назовем домедианой или предмедианой, а второй из них (который начинается в точке пересечения O, а заканчивается в точке его пересечения со стороной, противоположной вершине) мы назовем постмедианой.[1]
С помощью этих 2 понятий совсем просто формулируются некоторые теоремы геометрии. Например, в любом треугольнике отношение пред- и постмедианы равно двум.
Свойства[править | править код]
Основное свойство[править | править код]
Все три медианы треугольника пересекаются в одной точке, которая называется центроидом или центром тяжести треугольника, и делятся этой точкой на две части в отношении 2:1, считая от вершины.
Свойства медиан равнобедренного треугольника[править | править код]
В равнобедренном треугольнике две медианы, проведенные к равным сторонам треугольника, равны, а третья медиана одновременно является биссектрисой и высотой. Верно и обратное: если в треугольнике две медианы равны, то треугольник — равнобедренный, а третья медиана одновременно является биссектрисой и высотой угла при своей вершине.
У равностороннего треугольника все три медианы равны.
Свойства оснований медиан[править | править код]
- Теорема Эйлера для окружности девяти точек: основания трёх высот произвольного треугольника, середины трёх его сторон (основания его медиан) и середины трёх отрезков, соединяющих его вершины с ортоцентром, все лежат на одной окружности (так называемой окружности девяти точек).
- Отрезок, проведенный через основания двух любых медиан треугольника, является его средней линией. Средняя линия треугольника всегда параллельна той стороне треугольника, с которой она не имеет общих точек.
- Следствие (теорема Фалеса о параллельных отрезках). Средняя линия треугольника равна половине длины той стороны треугольника, которой она параллельна.
- Теркем доказал теорему Теркема.[2] Она утверждает, что если окружность девяти точек пересекает стороны треугольника или их продолжения в 3 парах точек (в 3 основаниях соответственно высот и медиан), являющихся основаниями 3 пар чевиан, то, если 3 чевианы для 3 из этих оснований пересекаются в 1 точке (например 3 медианы пересекаются в 1 точке), то 3 чевианы для 3 других оснований также пересекаются в 1 точке (т. е. 3 высоты также обязаны пересечься в 1 точке).
Другие свойства[править | править код]
- Если треугольник разносторонний (неравносторонний), то его биссектриса, проведённая из любой вершины, лежит между медианой и высотой, проведёнными из той же вершины.
- Медиана разбивает треугольник на два равновеликих (по площади) треугольника.
- Треугольник делится тремя медианами на шесть равновеликих треугольников. Центры описанных окружностей этих шести треугольников лежат на одной окружности, которая называется окружностью Ламуна.
- Из отрезков, образующих медианы, можно составить треугольник, площадь которого будет равна 3/4 от всего треугольника. Длины медиан удовлетворяют неравенству треугольника.
- В прямоугольном треугольнике медиана, проведённая из вершины с прямым углом, равняется половине гипотенузы.
- Большей стороне треугольника соответствует меньшая медиана.
- Отрезок прямой, симметричный или изогонально сопряжённый внутренней медиане относительно внутренней биссектрисы, называется симедианой треугольника. Три симедианы проходят через одну точку — точку Лемуана.
- Медиана угла треугольника изотомически сопряжена самой себе.
Бесконечно удаленная прямая — трилинейная поляра центроида
- Трилинейная поляра центроида (точки пересечения трех медиан) — бесконечно удаленная прямая (см. рис.).
Основные соотношения[править | править код]
Чтобы вычислить длину медианы, когда известны длины сторон треугольника, применяется теорема Аполлония (выводится через теорему Стюарта или достроением до параллелограмма и использованием равенства в параллелограмме суммы квадратов сторон и суммы квадратов диагоналей):
где — медианы к сторонам треугольника соответственно.
В частности, сумма квадратов медиан произвольного треугольника составляет 3/4 от суммы квадратов его сторон:
.
Обратно, можно выразить длину произвольной стороны треугольника через медианы:
где — медианы к соответствующим сторонам треугольника, — стороны треугольника.
Площадь любого треугольника, выраженная через длины его медиан:
где — полусумма длин медиан.
См. также[править | править код]
- Биссектриса
- Высота треугольника
- Инцентр
- Симедиана
- Центроид
- Чевиана
Примечания[править | править код]
Литература[править | править код]
- Ефремов Дм. Новая геометрия треугольника, 1902 год.
Источник
Медиана треугольника, так же, как и высота служит графическим параметром, определяющим весь треугольник, значение его сторон и углов. Три значения: медианы, высоты и биссектрисы – это, как штрих-код на товаре, наша задача просто уметь его считать.

Определение
Медиана – это отрезок, соединяющий высоту и середину противоположной стороны. В треугольнике три вершины, а значит и медианы три. Медианы не всегда совпадают с высотами или биссектрисами. Чаще всего это отдельные отрезки.
Свойства медиан
- Медиана равнобедренного треугольника, проведенная к основанию, совпадает с высотой и биссектрисой. В равностороннем треугольнике все медианы совпадают с биссектрисами и высотами.
- Все медианы треугольника пересекаются в одной точке.
- Медиана делит треугольник на два равновеликих, а три медианы, на 6 равновеликих треугольника.
Равновеликими называют треугольники, площади которых равны.
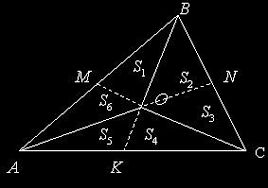
Рис. 1. Три медианы образуют 6 равновеликих треугольника.
- Точка пересечения медиан делит их в отношении 2:1, считая от вершины.
- Медиана, проведенная к гипотенузе прямоугольного треугольника, равна половине гипотенузы.
Задачи
Все эти свойства несложно запомнить, они легко закрепляются на практике. Для большего понимания темы, решим несколько задач:
- В прямоугольном треугольнике известны катеты, которые равны a=3 и b=4. Найти значение медианы m, проведенной к гипотенузе c.
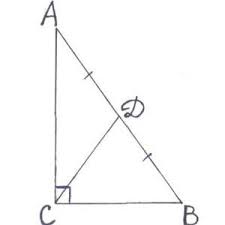
Рис. 2. Рисунок к задаче.
Для того, чтобы найти значение медианы, нам необходимо найти гипотенузу, так как медиана, проведенная к гипотенузе равна ее половине. Гипотенуза через теорему Пифагора: $$a^2+b^2=c^2$$
$$c=sqrt{a^2+b^2}=sqrt{9+16}=sqrt{25}=5$$
Найдем значение медианы: $$m={cover2}={5over2}=2,5$$ – получившееся число и есть значение медианы.
Значения медиан в треугольнике не равны. Поэтому нужно обязательно представлять, какую именно величину необходимо найти.
- В треугольнике известны значения сторон : a=7; b=8; c=9. Найти значение медианы, опущенной к стороне b.
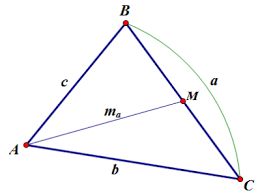
Рис. 3. Рисунок к задаче.
Чтобы решить эту задачу нужно воспользоваться одной из трех формул для нахождения медианы по сторонам треугольника:
$$m^2 ={1over2}*(a^2+c^2-b^2)$$
Как видно, главное здесь запомнить коэффициент при скобках и знаки у значения сторон. Знаки запомнить проще всего – вычитается всегда сторона, к которой опущена медиана. В нашем случае это b, но может быть любая другая.
Подставим значения в формулу и найдем величину медианы: $$m=sqrt{{1over2}*(a^2+c^2-b^2)}$$
$$m=sqrt{{1over2}*(49+81-64)}=sqrt{33}$$ – оставим результат в виде корня.
- В равнобедренном треугольнике медиана, проведенная к основанию равна 8, а само основание 6. Вместе с оставшимися двумя, эта медиана делит треугольник на 6 треугольников. Найти площадь каждого из них.
Медианы, разбивают треугольник на шесть равновеликих. Значит, площади малых треугольников будут равны между собой. Достаточно найти площадь большего и поделить ее на 6.
Дана медиана, проведенная к основанию, в равнобедренном треугольнике она является биссектрисой и высотой. Значит в треугольнике известны основание и высота. Можно найти площадь.
$$S={1over2}*6*8=24$$
Площадь каждого из малых треугольников: $${24over6}=4$$
Что мы узнали?
Мы узнали, что такое медиана. Определили свойства медианы, и нашли решение типовых задач. Поговорили о базовых ошибках и разобрались как просто и быстро запомнить формулу нахождения медианы через стороны треугольника.
Тест по теме
Оценка статьи
Средняя оценка: 4.7. Всего получено оценок: 137.
Источник
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Треугольники
- Свойства равнобедренного треугольника
1. Теорема
Дано:  АВС – равнобедренный, ВС – основание.
АВС – равнобедренный, ВС – основание.
Доказать:  В =
В =  С.
С.
Доказательство:
Проведем биссектрису АD из вершины А к стороне ВС.
Рассмотрим  АВD и
АВD и  АСD: АВ = АС по условию (
АСD: АВ = АС по условию ( АВС – равнобедренный), АD – общая сторона,
АВС – равнобедренный), АD – общая сторона,  BAD =
BAD =  CAD, так как АD – биссектриса по построению,
CAD, так как АD – биссектриса по построению, 
 АВD =
АВD =  АСD по первому признаку равенства треугольников
АСD по первому признаку равенства треугольников 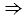
 В =
В =  С,потому что в равных треугольниках против равных сторон лежат равные углы (
С,потому что в равных треугольниках против равных сторон лежат равные углы ( В лежит против стороны АС,
В лежит против стороны АС,  С. – против стороны АВ).
С. – против стороны АВ).
Теорема доказана.
Справедливо и обратное утверждение:
Если в каком-либо треугольнике два угла равны, то такой треугольник равнобедренный.
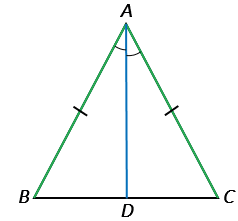
2. Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.
Дано:  АВС – равнобедренный, ВС – основание, АD – биссектриса.
АВС – равнобедренный, ВС – основание, АD – биссектриса.
Доказать: АD – медиана и высота.
Доказательство:

Рассмотрим  АВD и
АВD и  АСD: АВ = АС по условию (
АСD: АВ = АС по условию ( АВС – равнобедренный), АD – общая сторона,
АВС – равнобедренный), АD – общая сторона,  BAD =
BAD =  CAD, так как АD – биссектриса по условию,
CAD, так как АD – биссектриса по условию, 
 АВD =
АВD =  АСD по первому признаку равенства треугольников
АСD по первому признаку равенства треугольников  ВD = DC и
ВD = DC и  ADВ =
ADВ =  ADС.
ADС.
Мы доказали, что ВD = DC 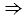 точка D – середина стороны ВС, тогда АD является медианой
точка D – середина стороны ВС, тогда АD является медианой  АВС (по определению медианы).
АВС (по определению медианы).
Мы доказали, что  ADВ =
ADВ =  ADС, причем
ADС, причем  ADВ и
ADВ и  ADС – смежные углы, поэтому
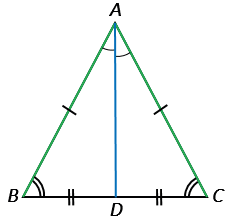
ADС – смежные углы, поэтому  ADВ +
ADВ +  ADС = 1800, тогда
ADС = 1800, тогда  ADВ =
ADВ =  ADС =900, т.е. АD
ADС =900, т.е. АD BC, а это означает, что AD является высотой
BC, а это означает, что AD является высотой  АВС (по определению высоты).
АВС (по определению высоты).
Теорема доказана.
Справедливо и обратное утверждение:
Если в каком-либо треугольнике медиана и высота совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника.
3. Теорема
В равнобедренном треугольнике высота, проведённая к основанию, является медианой и биссектрисой.
Справедливо и обратное утверждение:
Если в каком-либо треугольнике медиана и биссектриса совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника.
4. Теорема
В равнобедренном треугольнике медиана, проведённая к основанию, является высотой и биссектрисой.
Справедливо и обратное утверждение:
Если в каком-либо треугольнике высота и биссектриса совпадут, то такой треугольник равнобедренный, а сторона, к которой они проведены, основание данного треугольника.
Важно помнить, что данные теоремы справедливы только в том случае, если высота, медиана и биссектриса равнобедренного треугольника проведены к его ОСНОВАНИЮ.
Если треугольник равносторонний, то данные теоремы справедливы для медиан, биссектрис и высот, проведенных к каждой из сторон треугольника.
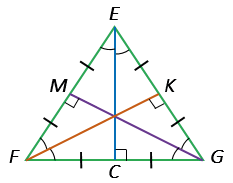
 EFG – равносторонний:
EFG – равносторонний:
- ЕС – биссектриса, медиана и высота, проведенная к стороне FG,
- FK – биссектриса, медиана и высота, проведенная к стороне ЕG,
- GM – биссектриса, медиана и высота, проведенная к стороне ЕF.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Треугольник
Равенство треугольников
Первый признак равенства треугольников
Перпендикуляр к прямой
Медианы треугольника
Биссектрисы треугольника
Высоты треугольника
Равнобедренный треугольник
Второй признак равенства треугольников
Третий признак равенства треугольников
Окружность
Построения циркулем и линейкой
Треугольники
Правило встречается в следующих упражнениях:
7 класс
Задание 119,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 6,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 420,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 436,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 515,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 18,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 726,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 900,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1057,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1275,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Источник
“Свойство медианы равнобедренного треугольника”
Цель: сформулировать и доказать теорему о свойстве медианы равнобедренного треугольника.
Задачи урока:
Углубить знания по теме «Равнобедренный треугольник»
сформулировать умение применения теоремы о свойстве медианы равнобедренного треугольника в стандартных и нестандартных ситуациях;
Развитие грамотной речи, развитие умений сравнивать, выявлять закономерности, обобщать, анализировать и делать выводы.
Воспитание интереса к предмету, настойчивости, воли при решении поставленной задачи.
Ход урока.
I.Организационная часть урока.
Мой юный друг!
Сегодня ты пришел вот в этот класс
На геометрии очередной урок,
Чтоб подвести изученному небольшой итог,
А также умом своим на новое взглянуть.
Пускай не станешь ты Евклидом. А вдруг?
Ведь столько не разгадано ещё вокруг?
Учитель: Кто ж такой Евклид?
Ученик: Евклид – древнегреческий ученый, живший в III веке до н.э.
Учитель: А в чем состоит заслуга Евклида?
Ученик: Его заслуга состоит в том, что он написал великий труд книгу «Начала».
Учитель: Из скольких частей состоят «Начала»?
Ученик: «Начала» состоят из 13 частей.
Учитель:Ребята, 9 из них посвящены вопросам геометрии и более двух тысяч лет геометрию изучали по этой книге. Поэтому геометрия, которую мы изучаем в школе называется…
Ученики: евклидовой.
Учитель: «Начала» считаются популярным рукописным памятником древности. Мировая наука начинается с геометрии. Ребята, большое место в «Началах» Евклида уделено сведениям о треугольниках. И в частности одному «удивительному» треугольнику. И, как вы догадались речь идет о равнобедренном треугольнике.
Ребята, а знаете ли вы, что среди равнобедренных треугольников есть «золотой» или «возвышенный»? Вы удивились этому? Сегодня на уроке мы с вами откроем еще одно свойство равнобедренного треугольника.
II.Устная работа.
Учитель: Ребята, внимание на доску. Ответьте, пожалуйста, на следующие вопросы:
Задание №1 (устно)
а) Какие из треугольников являются равнобедренными? Почему?
б) В равнобедренных треугольниках назовите основание и боковые стороны.
в) Назовите равные углы. Почему?

Задание №2 (устно):
а) Назовите треугольник, на котором изображена биссектриса. Почему?
б) Назовите треугольник, на котором изображена высота. Почему?
в) Назовите треугольник, на котором изображена медиана. Почему?

Задание №3 (в тетрадях): Начертите равнобедренный треугольник АВС, с основанием АВ.
Проведите в данном треугольнике медиану из вершины С к основанию АВ.
На этом же чертеже проводим высоту из вершины С к основанию АВ. И биссектрису угла С.
(В процессе построения вести диалог с учеником у доски и всем классом, объясняя каждый шаг построения).
Учитель: Ребята, что вы увидели? Какой вывод можно сделать, исходя из построения?
Мы это с вами сейчас сделали. Но геометрия – эта наука, в которой нельзя делать вывод, исходя из решения одной задачи. Всё, кроме аксиом, необходимо доказать. Поэтому переходим к изучению нового материала.
III. Постановка учебной задачи.Формирование новых понятий.
Цель: сформулировать и доказать свойство медианы равнобедренного треугольника.
Учитель: Ребята, запишите в тетрадях тему нашего урока «Свойство медианы равнобедренного треугольника». Ребята, скажите, пожалуйста, изучив сегодняшнюю тему, на какой вопрос в конце урока вы сможете ответить?
Да, действительно цель нашего урока сформулировать и доказать свойство медианы равнобедренного треугольника, и на примерах показать его применение.
Учитель: Ребята, займемся геометрическим исследованием (в результате исследования учащиеся должны сформулировать и доказать теорему о свойстве медианы равнобедренного треугольника). Результаты исследования должны быть представлены в виде схемы. Учащиеся вместе с учителем рассматривают рисунок и делают выводы.
Итак, перед нами рисунок. Узнай об этом треугольнике все что можно.
В результате исследования должна получиться следующая схема:
Учащиеся делают вывод: В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой, и ЗАПИСЫВАЮТ в тетрадях из учебника формулировку теоремы.
IV. Формирование умений и навыков.
Решение задач.
№1 (устно) В
Найдите ,
Если 0
С D А
№2
Начертите равнобедренный треугольник, основание которого равно 5см, а медиана проведенная к основанию равна 3,5см. (воспользуйтесь чертёжным треугольником и линейкой с делениями)
№3
Высота МТ КМР является бисссектрисой этого треугольника. Докажите, что данный треугольник является равноберенным.
Доказательство:
1.Рассмотрим треугольники …………… и ………….….:
Их элементы: ……………………… ……………………. ………………………………………………….
2.Воспользуемся………………………….. признаком, ………………………………………………………………………….
откуда, КМТ………………………..
3. Следовательно, ………………………..
Значит,……………………. является равнобедренным.
№4
На медиане BF равнобедренного АВС с основанием АС отмечена точка М. Докажите, что МА= МС.
Доказательство.
1.Рассмотрим АВМ и ……… :
АВ = ……… (по ………………………), сторона МВ- …………………………… АВМ= ……………, так как медиана ВF – ………………………………….. (по свойству ……………………………………).
2. Воспользуемся …………признаком …………….………………………………………………Получим, что ……..…….=……………,поэтому …………….=…………..
V.Подведение итогов.
Какой треугольник называется равнобедренным?
Каким свойством обладает равнобедренный треугольник?
Сколько медиан в треугольнике можно провести?
Каким свойством обладает медиана равнобедренного треугольника?
Этим свойством обладают все медианы в равнобедренном треугольнике?
Верно ли утверждение «Биссектриса, проведённая к основанию равнобедренного треугольника, является медианой и высотой?»
VI.Выставление оценок.
Учитель: Знания, накопленные в геометрии, использовались в архитектуре, в живописи. Древние зодчие, художники были прекрасными геометрами. использовали они и свойства равнобедренного треугольника, в частности «золотого треугольника» – у которого углы при основании по 720, а при вершине 360. Он обладает особым свойством: биссектриса угла при основании делит противолежащую сторону в золотом сечении. Равнобедренный треугольник основа пропорциональной сетки, которую используют художники и архитекторы при написании картин и создании прекрасных зданий.
Примеры. Миланский собор, картина Леонардо да Винчи «Джоконда».
VII.Домашнее задание: пункт 26, вопрос 11, №28.
ДЛЯ УСТНОЙ РАБОТЫ
Источник