Каким свойством обладает график четной функции
Функция – это одно из важнейших математических понятий. Функция – зависимость переменной у от переменной x, если каждому значению х соответствует единственное значение у. Переменную х называют независимой переменной или аргументом. Переменную у называют зависимой переменной. Все значения независимой переменной (переменной x) образуют область определения функции. Все значения, которые принимает зависимая переменная (переменная y), образуют область значений функции.
Графиком функции называют множество всех точек координатной плоскости, абсциссы которых равны значениям аргумента, а ординаты – соответствующим значениям функции, тоесть по оси абсцисс откладываются значения переменной x, а по оси ординат откладываются значения переменной y. Для построения графика функции необходимо знать свойства функции. Основные свойства функции будут рассмотрены далее!
Для построения графика функции советуем использовать нашу программу – Построение графиков функций онлайн. Если при изучении материала на данной странице у Вас возникнут вопросы, Вы всегда можете задать их на нашем форуме. Также на форуме Вам помогут решить задачи по математике, химии, геометрии, теории вероятности и многим другим предметам!
Основные свойства функций.
1) Область определения функции и область значений функции.
Область определения функции – это множество всех допустимых действительных значений аргумента x (переменной x), при которых функция y = f(x) определена.
Область значений функции – это множество всех действительных значений y, которые принимает функция.
В элементарной математике изучаются функции только на множестве действительных чисел.
2) Нули функции.
Значения х, при которых y=0, называется нулями функции. Это абсциссы точек пересечения графика функции с осью Ох.
3) Промежутки знакопостоянства функции.
Промежутки знакопостоянства функции – такие промежутки значений x, на которых значения функции y либо только положительные, либо только отрицательные, называются промежутками знакопостоянства функции.
4) Монотонность функции.
Возрастающая функция (в некотором промежутке) – функция, у которой большему значению аргумента из этого промежутка соответствует большее значение функции.
Убывающая функция (в некотором промежутке) – функция, у которой большему значению аргумента из этого промежутка соответствует меньшее значение функции.
5) Четность (нечетность) функции.
Четная функция – функция, у которой область определения симметрична относительно начала координат и для любого хиз области определения выполняется равенство f(-x) = f(x). График четной функции симметричен относительно оси ординат.
Нечетная функция – функция, у которой область определения симметрична относительно начала координат и для любогох из области определения справедливо равенство f(-x) = – f(x). График нечетной функции симметричен относительно начала координат.
Четная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0), то есть если точка a принадлежит области определения, то точка -a также принадлежит области определения.
2) Для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=f(x)
3) График четной функции симметричен относительно оси Оу.
Нечетная функция обладает следующими свойствами:
1) Область определения симметрична относительно точки (0; 0).
2) для любого значения x, принадлежащего области определения , выполняется равенство f(-x)=-f(x)
3) График нечетной функции симметричен относительно начала координат (0; 0).
Не всякая функция является четной или нечетной. Функции общего вида не являются ни четными, ни нечетными.
6) Ограниченная и неограниченная функции.
Функция называется ограниченной, если существует такое положительное число M, что |f(x)| ≤ M для всех значений x . Если такого числа не существует, то функция – неограниченная.
7) Периодическость функции.
Функция f(x) – периодическая, если существует такое отличное от нуля число T, что для любого x из области определения функции имеет место: f(x+T) = f(x). Такое наименьшее число называется периодом функции. Все тригонометрические функции являются периодическими. (Тригонометрические формулы).
Функция f называется периодической, если существует такое число , что при любом x из области определения выполняется равенство f(x)=f(x-T)=f(x+T). T – это период функции.
Всякая периодическая функция имеет бесконечное множество периодов. На практике обычно рассматривают наименьший положительный период.
Значения периодической функции через промежуток, равный периоду, повторяются. Это используют при построении графиков.
Источник
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
(blacktriangleright) Функция (f(x)) называется четной, если при всех (x) из ее области определения верно: (f(-x)=f(x)).
График четной функции симметричен относительно оси (y):
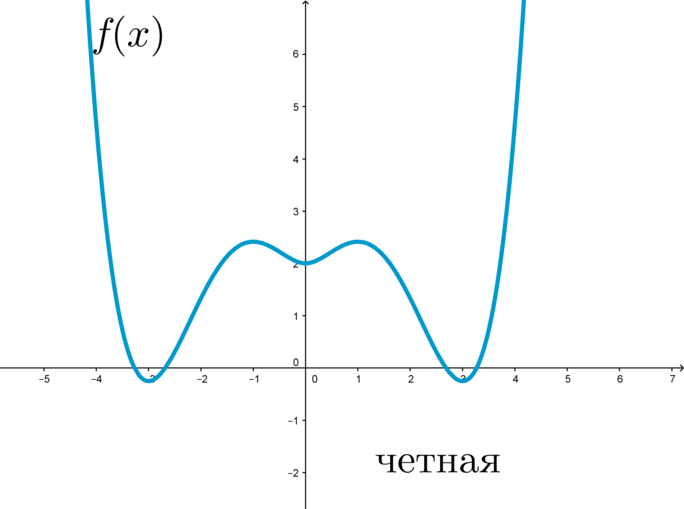
Пример: функция (f(x)=x^2+cos x) является четной, т.к. (f(-x)=(-x)^2+cos{(-x)}=x^2+cos x=f(x)).
(blacktriangleright) Функция (f(x)) называется нечетной, если при всех (x) из ее области определения верно: (f(-x)=-f(x)).
График нечетной функции симметричен относительно начала координат:
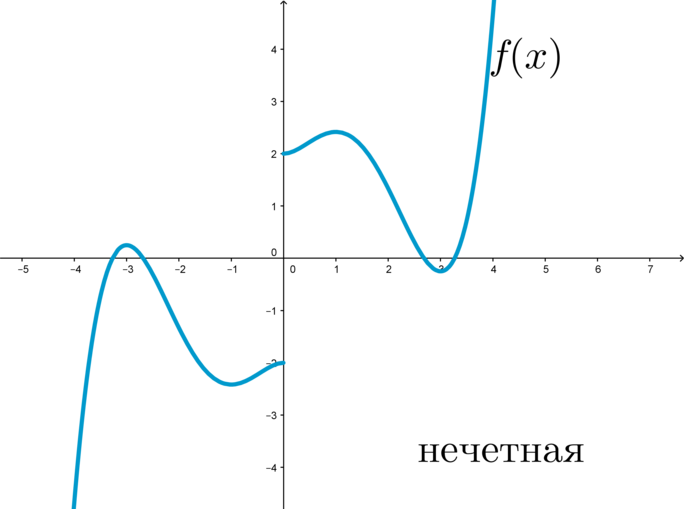
Пример: функция (f(x)=x^3+x) является нечетной, т.к. (f(-x)=(-x)^3+(-x)=-x^3-x=-(x^3+x)=-f(x)).
(blacktriangleright) Функции, не являющиеся ни четными, ни нечетными, называются функциями общего вида. Такую функцию можно всегда единственным образом представить в виде суммы четной и нечетной функции.
Например, функция (f(x)=x^2-x) является суммой четной функции (f_1=x^2) и нечетной (f_2=-x).
(blacktriangleright) Некоторые свойства:
1) Произведение и частное двух функций одинаковой четности — четная функция.
2) Произведение и частное двух функций разной четности — нечетная функция.
3) Сумма и разность четных функций — четная функция.
4) Сумма и разность нечетных функций — нечетная функция.
5) Если (f(x)) — четная функция, то уравнение (f(x)=c (cin
mathbb{R})) имеет единственный корень тогда и только когда, когда (x=0).
6) Если (f(x)) — четная или нечетная функция, и уравнение (f(x)=0) имеет корень (x=b), то это уравнение обязательно будет иметь второй корень (x=-b).
(blacktriangleright) Функция (f(x)) называется периодической на (X), если для некоторого числа (Tne 0) выполнено (f(x)=f(x+T)), где (x,
x+Tin X). Наименьшее (T), для которого выполнено данное равенство, называется главным (основным) периодом функции.
У периодической функции любое число вида (nT), где (nin mathbb{Z}) также будет являться периодом.
Пример: любая тригонометрическая функция является периодической;
у функций (f(x)=sin x) и (f(x)=cos x) главный период равен (2pi), у функций (f(x)=mathrm{tg},x) и (f(x)=mathrm{ctg},x) главный период равен (pi).
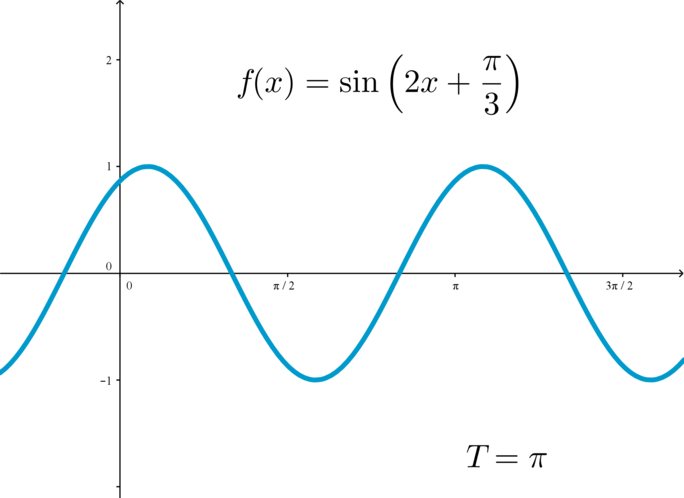
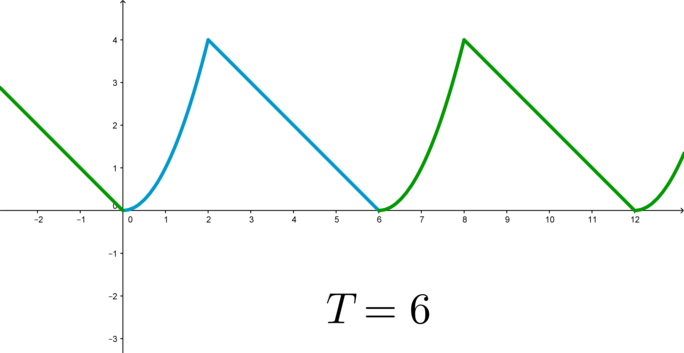
Для того, чтобы построить график периодической функции, можно построить ее график на любом отрезке длиной (T) (главный период); тогда график всей функции достраивается сдвигом построенной части на целое число периодов вправо и влево:
(blacktriangleright) Область определения (D(f)) функции (f(x)) — это множество, состоящее из всех значений аргумента (x), при которых функция имеет смысл (определена).
Пример: у функции (f(x)=sqrt x+1) область определения: (xin
[0;+infty)).
(blacktriangleright) Область значений (E(f)) функции (f(x)) — это множество, состоящее из всех значений функции (f(a)), где (ain
D(f)).
Пример: у функции (f(x)=sqrt x +1) область значений: (f(x)in
[1;+infty)).
(blacktriangleright) Уравнение (f(x)=a) имеет решение тогда и только тогда, когда (a) принадлежит области значений функции (f(x)), т.е. (ain E(f)).
(blacktriangleright) Если область значений функции (f(x)) не превышает некоторого числа (A), т.е. (f(x)leq A) при всех (xin
D(f)), а функция (g(x)geq A) при всех (xin D(g)), то уравнение [{large{f(x)=g(x)}} Leftrightarrow begin{cases} f(x)=A\g(x)=Aend{cases}]
Задание
1
#6364
Уровень задания: Равен ЕГЭ
При каких значениях параметра (a) уравнение
[2x^2+amathrm{tg},(cos x)+a^2=0]
имеет единственное решение?
Заметим, что так как (x^2) и (cos x) — четные функции, то если уравнение будет иметь корень (x_0), оно также будет иметь и корень (-x_0).
Действительно, пусть (x_0) – корень, то есть равенство (2x_0^2+amathrm{tg},(cos x_0)+a^2=0) верно. Подставим (-x_0): (2
(-x_0)^2+amathrm{tg},(cos(-x_0))+a^2=2x_0^2+amathrm{tg},(cos
x_0)+a^2=0).
Таким образом, если (x_0ne 0), то уравнение уже будет иметь как минимум два корня. Следовательно, (x_0=0). Тогда:
[2cdot 0+amathrm{tg},(cos 0)+a^2=0 quad Rightarrow quad
a^2+amathrm{tg},1=0 quad Rightarrow quad left[
begin{gathered}begin{aligned}
&a=0\
&a=-mathrm{tg},1 end{aligned} end{gathered}right.]
Мы получили два значения параметра (a). Заметим, что мы использовали то, что (x=0) точно является корнем исходного уравнения. Но мы нигде не использовали то, что он единственный. Следовательно, нужно подставить получившиеся значения параметра (a) в исходное уравнение и проверить, при каких именно (a) корень (x=0) действительно будет единственным.
1) Если (a=0), то уравнение примет вид (2x^2=0). Очевидно, что это уравнение имеет лишь один корень (x=0). Следовательно, значение (a=0) нам подходит.
2) Если (a=-mathrm{tg},1), то уравнение примет вид [2x^2-mathrm{tg},1cdot mathrm{tg},(cos x)+mathrm{tg}^2,1=0] Перепишем уравнение в виде [2x^2+mathrm{tg}^2,1=mathrm{tg},1cdot mathrm{tg},(cos x)qquad (*)] Так как (-1leqslant cos xleqslant 1), то (-mathrm{tg},1leqslant mathrm{tg},(cos x)leqslant
mathrm{tg},1). Следовательно, значения правой части уравнения (*) принадлежат отрезку ([-mathrm{tg}^2,1; mathrm{tg}^2,1]).
Так как (x^2geqslant 0), то левая часть уравнения (*) больше или равна (0+
mathrm{tg}^2,1).
Таким образом, равенство (*) может выполняться только тогда, когда обе части уравнения равны (mathrm{tg}^2,1). А это значит, что [begin{cases} 2x^2+mathrm{tg}^2,1=mathrm{tg}^2,1 \
mathrm{tg},1cdot mathrm{tg},(cos x)=mathrm{tg}^2,1
end{cases}
quadLeftrightarrowquad begin{cases} x=0\
mathrm{tg},(cos x)=mathrm{tg},1
end{cases}quadLeftrightarrowquad x=0] Следовательно, значение (a=-mathrm{tg},1) нам подходит.
Ответ:
(ain {-mathrm{tg},1;0})
Задание
2
#3923
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых график функции [f(x)=3mathrm{tg},dfrac{ax}5 +2sin dfrac{8pi a-3x}4]
симметричен относительно начала координат.
Если график функции симметричен относительно начала координат, то такая функция является нечетной, то есть выполнено (f(-x)=-f(x)) для любого (x) из области определения функции. Таким образом, требуется найти те значения параметра, при которых выполнено (f(-x)=-f(x).)
[begin{aligned}
&3mathrm{tg},left(-dfrac{ax}5right)+2sin dfrac{8pi a+3x}4=
-left(3mathrm{tg},left(dfrac{ax}5right)+2sin dfrac{8pi
a-3x}4right)quad Rightarrowquad -3mathrm{tg},dfrac{ax}5+2sin
dfrac{8pi a+3x}4=
-left(3mathrm{tg},left(dfrac{ax}5right)+2sin dfrac{8pi
a-3x}4right) quad Rightarrow\[3ex]
Rightarrowquad &sin dfrac{8pi a+3x}4+sin dfrac{8pi a-3x}4=0
quad Rightarrow quad2sin dfrac12left(dfrac{8pi
a+3x}4+dfrac{8pi a-3x}4right)cdot cos dfrac12
left(dfrac{8pi a+3x}4-dfrac{8pi a-3x}4right)=0 quad
Rightarrowquad sin (2pi a)cdot cos frac34 x=0
end{aligned}]
Последнее уравнение должно быть выполнено для всех (x) из области определения (f(x)), следовательно, (sin(2pi a)=0 Rightarrow
a=dfrac n2, ninmathbb{Z}).
Ответ:
(dfrac n2, ninmathbb{Z})
Задание
3
#3069
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение [f(x)=|a+2|sqrt[3]x] имеет 4 решения, где (f) – четная периодическая с периодом (T=dfrac{16}3) функция, определенная на всей числовой прямой, причем (f(x)=ax^2) при (0leqslant xleqslant dfrac83.)
(Задача от подписчиков)
Так как (f(x)) – четная функция, то ее график симметричен относительно оси ординат, следовательно, при (-dfrac83leqslant
xleqslant 0) (f(x)=ax^2). Таким образом, при (-dfrac83leqslant
xleqslant dfrac83), а это отрезок длиной (dfrac{16}3), функция (f(x)=ax^2).
1) Пусть (a>0). Тогда график функции (f(x)) будет выглядеть следующим образом: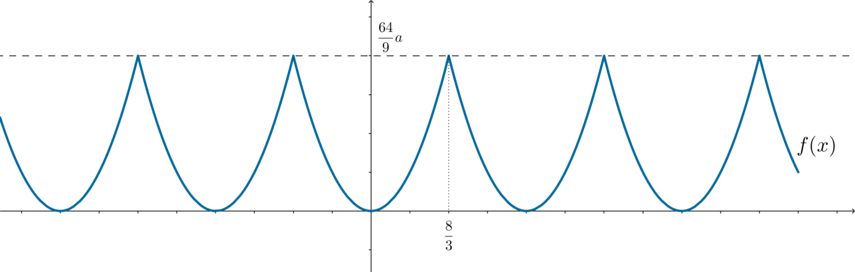
Тогда для того, чтобы уравнение имело 4 решения, нужно, чтобы график (g(x)=|a+2|cdot sqrt[3]x) проходил через точку (A):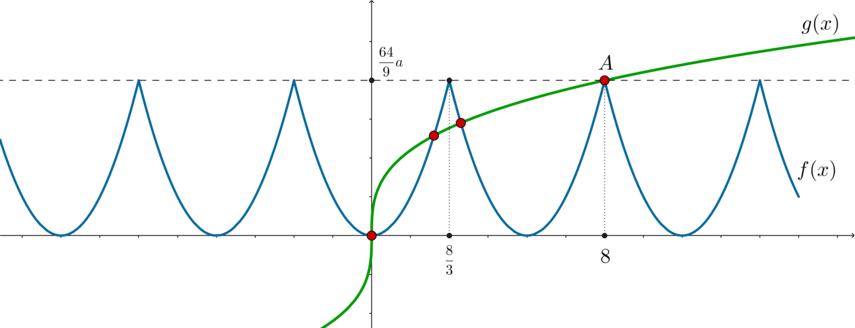
Следовательно, [dfrac{64}9a=|a+2|cdot sqrt[3]8 quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &9(a+2)=32a\
&9(a+2)=-32a end{aligned} end{gathered}right.
quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &a=dfrac{18}{23}\[2ex]
&a=-dfrac{18}{41} end{aligned} end{gathered}right.] Так как (a>0), то подходит (a=dfrac{18}{23}).
2) Пусть (a<0). Тогда картинка окажется симметричной относительно начала координат: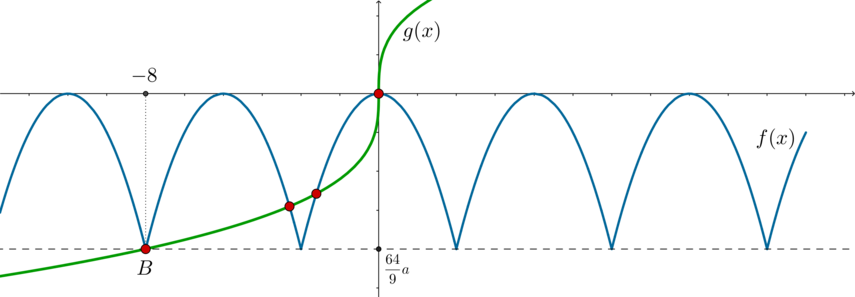
Нужно, чтобы график (g(x)) прошел через точку (B): [dfrac{64}9a=|a+2|cdot sqrt[3]{-8} quadLeftrightarrowquad
left[begin{gathered}begin{aligned} &a=dfrac{18}{23}\[2ex]
&a=-dfrac{18}{41} end{aligned} end{gathered}right.] Так как (a<0), то подходит (a=-dfrac{18}{41}).
3) Случай, когда (a=0), не подходит, так как тогда (f(x)=0) при всех (x), (g(x)=2sqrt[3]x) и уравнение будет иметь только 1 корень.
Ответ:
(ain left{-dfrac{18}{41};dfrac{18}{23}right})
Задание
4
#3072
Уровень задания: Равен ЕГЭ
Найдите все значения (a), при каждом из которых уравнение [a^2-7a+7sqrt{2x^2+49}=3|x-7a|-6|x|]
имеет хотя бы один корень.
(Задача от подписчиков)
Перепишем уравнение в виде [7sqrt{2x^2+49}=3|x-7a|-6|x|-a^2+7a] и рассмотрим две функции: (g(x)=7sqrt{2x^2+49}) и (f(x)=3|x-7a|-6|x|-a^2+7a).
Функция (g(x)) является четной, имеет точку минимума (x=0) (причем (g(0)=49)).
Функция (f(x)) при (x>0) является убывающей, а при (x<0) – возрастающей, следовательно, (x=0) – точка максимума.
Действительно, при (x>0) второй модуль раскроется положительно ((|x|=x)), следовательно, вне зависимости от того, как раскроется первый модуль, (f(x)) будет равно (kx+A), где (A) – выражение от (a), а (k) равно либо (-9), либо (-3). При (x<0) наоборот: второй модуль раскроется отрицательно и (f(x)=kx+A), где (k) равно либо (3), либо (9).
Найдем значение (f) в точке максимума: [f(0)=-a^2+7a+21|a|]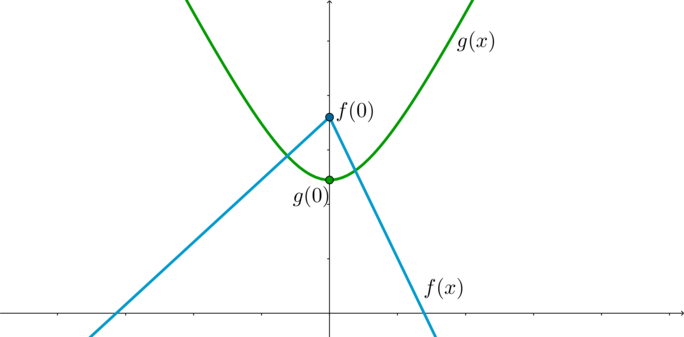
Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций (f) и (g) имели хотя бы одну точку пересечения. Следовательно, нужно: [f(0)geqslant g(0) quadRightarrowquad -a^2+7a+21|a|geqslant 49
quadLeftrightarrowquad left[ begin{gathered} begin{aligned}
&begin{cases} a>0\
a^2-28a+49leqslant 0 end{cases}\
&begin{cases} a<0\
a^2+14a+49leqslant 0 end{cases}\
&begin{cases} a=0\
0geqslant 49end{cases} end{aligned} end{gathered}right.] Решая данную совокупность систем, получим ответ: [ain {-7}cup [14-7sqrt3;14+7sqrt3]]
Ответ:
(ain {-7}cup[14-7sqrt3;14+7sqrt3])
Задание
5
#3912
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение [2^{x^3-3x^2+4}+(a-10)cdot (sqrt2)^{x^3-3x^2+4}+12-a=0]
имеет шесть различных решений.
Сделаем замену ((sqrt2)^{x^3-3x^2+4}=t), (t>0). Тогда уравнение примет вид [t^2+(a-10)t+12-a=0quad (*)] Будем постепенно выписывать условия, при которых исходное уравнение будет иметь шесть решений.
Заметим, что квадратное уравнение ((*)) может максимум иметь два решения. Любое кубическое уравнение (Ax^3+Bx^2+Cx+D=0) может иметь не более трех решений. Следовательно, если уравнение ((*)) имеет два различных решения (положительных!, так как (t) должно быть больше нуля) (t_1) и (t_2), то, сделав обратную замену, мы получим: [left[begin{gathered}begin{aligned}
&(sqrt2)^{x^3-3x^2+4}=t_1\[2ex]
&(sqrt2)^{x^3-3x^2+4}=t_2end{aligned}end{gathered}right.] Так как любое положительное число можно представить как (sqrt2) в какой-то степени, например, (t_1=(sqrt2)^{log_{sqrt2} t_1}), то первое уравнение совокупности перепишется в виде [x^3-3x^2+4=log_{sqrt2} t_1] Как мы уже говорили, любое кубическое уравнение имеет не более трех решений, следовательно, каждое уравнение из совокупности будет иметь не более трех решений. А значит и вся совокупность будет иметь не более шести решений.
Значит, чтобы исходное уравнение имело шесть решений, квадратное уравнение ((*)) должно иметь два различных решения, а каждое полученное кубическое уравнение (из совокупности) должно иметь три различных решения (причем ни одно решение одного уравнения не должно совпадать с каким-либо решением второго!)
Очевидно, что если квадратное уравнение ((*)) будет иметь одно решение, то мы никак не получим шесть решений у исходного уравнения.
Таким образом, план решения становится ясен. Давайте по пунктам выпишем условия, которые должны выполняться.
1) Чтобы уравнение ((*)) имело два различных решения, его дискриминант должен быть положительным: [D=a^2-16a+52>0quadLeftrightarrowquad
ain (-infty;8-2sqrt3)cup(8+2sqrt3;+infty)]
2) Также нужно, чтобы оба корня были положительными (так как (t>0)). Если произведение двух корней положительное и сумма их положительная, то и сами корни будут положительными. Следовательно, нужно: [begin{cases} 12-a>0\-(a-10)>0end{cases}quadLeftrightarrowquad a<10]
Таким образом, мы уже обеспечили себе два различных положительных корня (t_1) и (t_2).
3) Давайте посмотрим на такое уравнение [x^3-3x^2+4=log_{sqrt2} t] При каких (t) оно будет иметь три различных решения?
Рассмотрим функцию (f(x)=x^3-3x^2+4).
Можно разложить на множители: [x^3-3x^2+4=x^3+x^2-4x^2+4=x^2(x+1)-4(x+1)(x-1)=(x+1)(x-2)^2] Следовательно, ее нули: (x=-1;2).
Если найти производную (f'(x)=3x^2-6x), то мы получим две точки экстремума (x_{max}=0, x_{min}=2).
Следовательно, график выглядит так: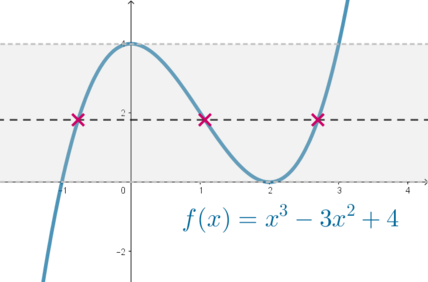
Мы видим, что любая горизонтальная прямая (y=k), где (0<k<4), пересекает график в трех точках. При всех остальных значениях (k) будет меньше трех точек пересечения. Следовательно, для того, чтобы уравнение (x^3-3x^2+4=log_{sqrt2} t) имело три различных решения, нужно, чтобы (0<log_ {sqrt2}t<4).
Таким образом, нужно: [begin{cases} 0<log_{sqrt2}t_1<4\ 0<log_{sqrt2}t_2<4end{cases}qquad (**)] Давайте также сразу заметим, что если числа (t_1) и (t_2) различны, то и числа (log_{sqrt2}t_1) и (log_{sqrt2}t_2) будут различны, значит, и уравнения (x^3-3x^2+4=log_{sqrt2} t_1) и (x^3-3x^2+4=log_{sqrt2} t_2) будут иметь несовпадающие между собой корни.
Систему ((**)) можно переписать так: [begin{cases} 1<t_1<4\
1<t_2<4end{cases}]
Таким образом, мы определили, что оба корня уравнения ((*)) должны лежать в интервале ((1;4)). Как записать это условие?
В явном виде выписывать корни мы не будем.
Рассмотрим функцию (g(t)=t^2+(a-10)t+12-a). Ее график – парабола с ветвями вверх, которая имеет две точки пересечения с осью абсцисс (это условие мы записали в пункте 1)). Как должен выглядеть ее график, чтобы точки пересечения с осью абсцисс были в интервале ((1;4))? Так: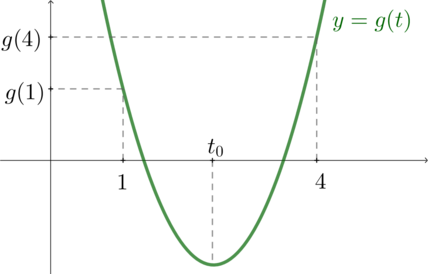
Во-первых, значения (g(1)) и (g(4)) функции в точках (1) и (4) должны быть положительными, во-вторых, вершина параболы (t_0) должна также находиться в интервале ((1;4)). Следовательно, можно записать систему: [begin{cases}
1+a-10+12-a>0\[1ex]
4^2+(a-10)cdot 4+12-a>0\[2ex]
1<dfrac{-(a-10)}2<4end{cases}quadLeftrightarrowquad 4<a<8]
Таким образом, нам нужно пересечь значения параметра (a), найденные в 1-ом, 2-ом и 3-ем пунктах, и мы получим ответ: [begin{cases} ain (-infty;8-2sqrt3)cup(8+2sqrt3;+infty)\ a<10\
4<a<8end{cases}quadLeftrightarrowquad 4<a<8-2sqrt3]
Ответ:
((4;8-2sqrt3))
Задание
6
#1828
Уровень задания: Равен ЕГЭ
Найдите все значения параметра (a), при каждом из которых уравнение
[25x^5+25(a-1)x^3-4(a-7)x=0]
имеет ровно пять различных решений, а сами решения, упорядоченные по возрастанию, образуют арифметическую прогрессию.
Заметим, что данное уравнение при любых значениях (a) всегда имеет как минимум один корень (x=0). Значит, для выполнения условия задачи нужно, чтобы уравнение [25x^4+25(a-1)x^2-4(a-7)=0 qquad (*)]
имело четыре различных корня, отличных от нуля, представляющих вместе с (x=0) арифметическую прогрессию.
Заметим, что функция (y=25x^4+25(a-1)x^2-4(a-7)) является четной, значит, если (x_0) является корнем уравнения ((*)), то и (-x_0) будет являться его корнем. Тогда необходимо, чтобы корнями этого уравнения были упорядоченные по возрастанию числа: (-2d, -d, d, 2d) (тогда (d>0)). Именно тогда данные пять чисел будут образовывать арифметическую прогрессию (с разностью (d)).
Чтобы этими корнями являлись числа (-2d, -d, d, 2d), нужно, чтобы числа (d^{,2}, 4d^{,2}) являлись корнями уравнения (25t^2+25(a-1)t-4(a-7)=0). Тогда по теореме Виета:
[begin{cases}
-dfrac{4(a-7)}{25}=d^{,2}cdot 4d^{,2}\[4pt]
-dfrac{25(a-1)}{25}=d^{,2}+4d^{,2}
end{cases} quad Rightarrow quad begin{cases}
d^{,4}=dfrac{7-a}{25}\
dfrac{7-a}{25}=left(dfrac{1-a}{5}right)^2
end{cases} quad Rightarrow quad
left[begin{gathered}begin{aligned} &a=-2\&a=3
end{aligned} end{gathered} right.]
Причем при (a=-2) (d=pm sqrt{frac35}), а при (a=3) (din
varnothing). Значит, подходит значение (a=-2) и (d=sqrt{frac35}) (т.к. должно быть (d>0)).
Ответ:
(ain {-2})
Задание
7
#3198
Уровень задания: Равен ЕГЭ
Найдите все значения (a), при каждом из которых уравнение [a^2+13|x|+2^{x^2+2}=20a+2|5x+12a|]
имеет хотя бы один корень.
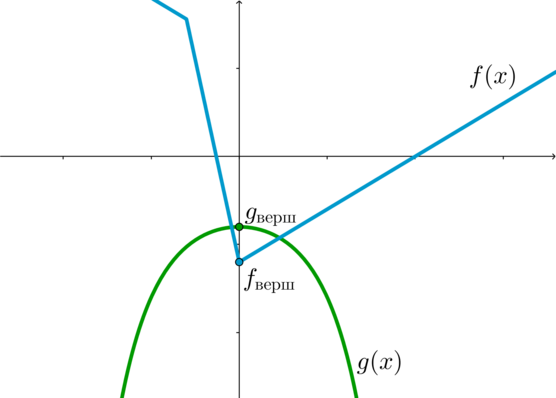
Перепишем уравнение в виде [13|x|-2|5x+12a|=20a-a^2-2^{x^2+2}] и рассмотрим две функции: (g(x)=20a-a^2-2^{x^2+2}) и (f(x)=13|x|-2|5x+12a|).
Функция (g(x)) имеет точку максимума (x=0) (причем (g_{text{верш}}=g(0)=-a^2+20a-4)):
(g'(x)=-2^{x^2+2}cdot ln 2cdot 2x). Ноль производной: (x=0). При (x<0) имеем: (g’>0), при (x>0): (g'<0).
Функция (f(x)) при (x>0) является возрастающей, а при (x<0) – убывающей, следовательно, (x=0) – точка минимума.
Действительно, при (x>0) первый модуль раскроется положительно ((|x|=x)), следовательно, вне зависимости от того, как раскроется второй модуль, (f(x)) будет равно (kx+A), где (A) – выражение от (a), а (k) равно либо (13-10=3), либо (13+10=23). При (x<0) наоборот: первый модуль раскроется отрицательно и (f(x)=kx+A), где (k) равно либо (-3), либо (-23).
Найдем значение (f) в точке минимума: [f_{text{верш}}=f(0)=-24|a|]
Для того, чтобы уравнение имело хотя бы одно решение, нужно, чтобы графики функций (f) и (g) имели хотя бы одну точку пересечения. Следовательно, нужно: [f(0)leqslant g(0) quadRightarrowquad a^2-20a+4leqslant 24|a|
quadLeftrightarrowquad left[ begin{gathered} begin{aligned}
&begin{cases} ageqslant 0\
a^2-44a+4leqslant 0 end{cases}\
&begin{cases} a<0\
a^2+4a+4leqslant 0 end{cases} end{aligned}
end{gathered}right.] Решая данную совокупность систем, получим ответ: [ain {-2}cup[22-4sqrt{30};22+4sqrt{30}]]
Ответ:
(ain {-2}cup[22-4sqrt{30};22+4sqrt{30}])
Источник
