Каким свойством обладает биссектриса треугольника
Мария Полютова
20 февраля 2019 · 15,6 K
Имею естественно научное образование, в юношестве прикипел к литературе, сейчас…
Основные свойства бисскетрисы:
- Делит противовположные стороны на части, которые пропорциональные прилегающим сторонам
- Все биссектрисы пересекаются в точке внутри треугольника, и эта точка является центром окружности, вписанной в треугольник
- Точки биссектрисы равноудалены от точек ее угла
- Бисскетрисы внешнего и внутреннего уголов прямоугольника являются перпендикулярными
- Бисскетриса является и медианой и высотой только в правильном треугольнике
Биссектриса является медийной и высотой и в равнобедренном треугольнике
Геометрия как быстро выучить что такое треугольник высота медиана биссектриса?
Высота значит точно то же, что и в обычном мире 🙂 То есть расстояние от вершины (она может быть любой) до той линии, на которой треугольник “стоит”.
Медиана соединяет вершину с центром стороны напротив.
Биссектриса делит угол пополам, выходя из вершины “внутрь”.
Высоты – из вершин к плоскости, на которой треугольник может “стоять”. Тоесть под прямым углом сверху-вниз.
Медиана – делит сторону напротив угла пополам
Биссектриса – делит пополам сам угол
Прочитать ещё 2 ответа
Возможен ли не прямоугольный треугольник, в котором сумма квадратов двух сторон равна квадрату третьей стороны?
Я согласен с ответом от Uwe Boll, но постараюсь ответить более детально.
Вообще, если вам даны один угол и длина двух сторон, или два угла и длина одной стороны, или все три стороны, то они определяют остальные три элемента. Однако если вам даны три угла, то они определяют длину сторон с точностью до фактора.
В вашем вопросе, даны длины всех трех сторон с точностью до фактора:
fA, fB, и fC=f sqrt(A^2+B^2). Мы хотим понять почему никакой “гибкости” в этом треугольнике нет.
Обозначим углы напротив каждой из сторон соотвенственно a, b, c .
Мы используем закон косинусов на плоскости:
Косинус угла напротив “длинной” стороны (мы подозреваем, гипотенузы) определен
cos(c) = (A^2 + B^2 – C^2) / (2AB)
(фактор f сокращается). (Заметим, что два других угла тоже определены без всякой гибкости, но нам они не интересны.) Дальже идет алгебра – мы знаем длину C(A,B) и подставляем в правую сторону:
(A^2 + B^2 – C^2) / (2AB) = (A^2 + B^2 – sqrt(A^2+B^2)^2) / (2AB) = (A^2 + B^2 – (A^2+B^2)) / (2AB) = 0.
То есть косинус угла c = ноль. Значит это должен быть прямой угол.
Однако закон косинусов так не работает, если ваш треугольник не на плоскости, а, например, на сфере.
Прочитать ещё 2 ответа
Чему равно число Пи?
Никто не знает точно, чему равно пи. Если разделить длину окружности на ее диаметр, то результат всегда будет одинаковый, какую окружность ни возьми. Этот результат и обозначили греческой буквой пи. Буква понадобилась потому, что привычными цифрами это число точно записать невозможно. Но мы знаем, чему оно равно приблизительно.
Самое знаменитое приближение – 3,14. Чтобы запомнить больше цифр, можно выучить стишок:
Надо очень постараться
И запомнить всё как есть:
Три, четырнадцать, пятнадцать,
Девяносто два и шесть
Прочитать ещё 17 ответов
Какие четыре точки называют “замечательными точками” треугольника?
Замечательных точек треугольника много, все не перечесть 🙂
Четыре самые знаменитые, их изучают в школе:
- Центр масс — точка пересечения медиан треугольника
- Центр описанной около треугольника окружности — точка пересечения серединных перпендикуляров
- Центр вписанной в треугольник окружности — точка пересечения биссектрис
- Ортоцентр — точка пересечения высот треугольника
Вот еще примеры замечательных точек:
- Точка Жергонна — точка пересечения прямых, проходящих через точки касания вписанной окружности со сторонами треугольника и противолежащие вершины.
- Точка Нагеля — точка пересечения прямых, проходящих через точки касания вневписанных окружностей со сторонами треугольника и противолежащие вершины
- Точка Лемуана — точка, изогонально сопряжённая точке пересечения медиан, то есть точка пересечения прямых, симметричных медианам относительно соответствующих биссектрис треугольника
Есть еще много других
Прочитать ещё 1 ответ
Источник
Базовым понятием и одним из наиболее интересных и полезных объектов школьной математики является биссектриса. С её помощью доказываются многие положения планиметрии, упрощается решение задач.
Известные свойства позволяют рассматривать геометрические фигуры с разных точек зрения. Появляется вариативность при выборе пути доказательств.
Становится возможным использование инструмента алгебры, например, свойство пропорции, нахождение неизвестных величин, решение алгебраических уравнений при рассмотрении геометрических вопросов.
Что такое биссектриса в геометрии
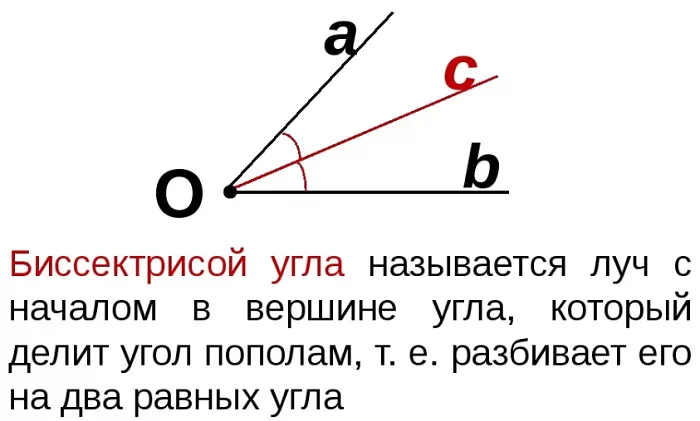
Рассматривают луч, выходящий из вершины угла или его часть (отрезок), который делит угол пополам. Такой луч (или, соответственно, отрезок) называется биссектрисой.
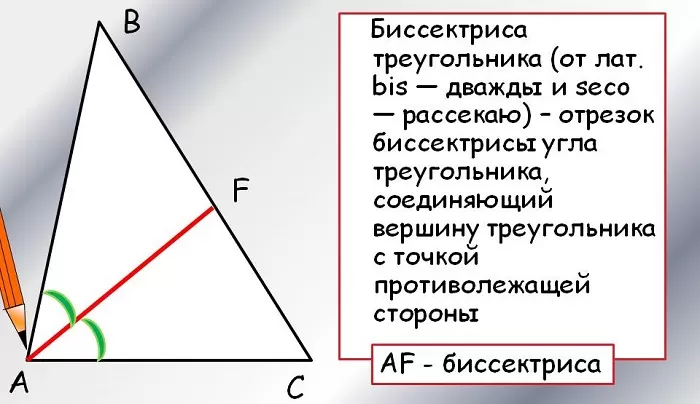
Часто для треугольников определение немного сужают, говоря об отрезке, соединяющем вершину угла, делящем его пополам, с точкой на противолежащей стороне. При этом рассматривается внутренняя область фигуры.
В то же время, часто при решении задач используются прямые, делящие внешние углы на два равных.
Биссектриса прямоугольного треугольника
Для прямоугольного треугольника одна из биссектрис образует равные углы, величины которых хорошо просчитываются (45 градусов).
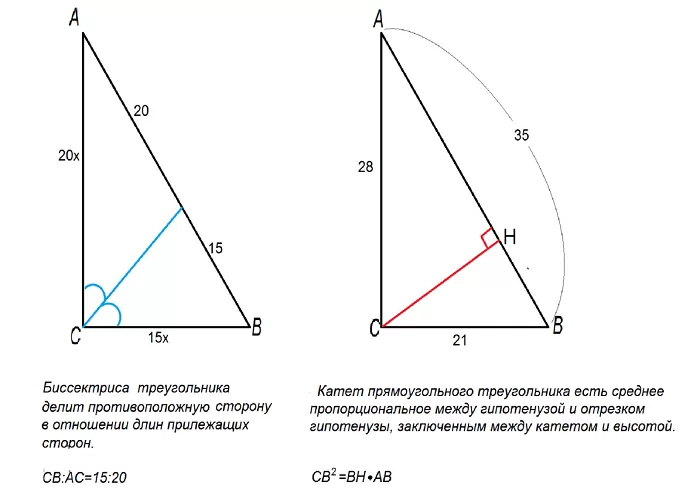
Это помогает вычислять углы при решении задач, связанных с фигурами, которые можно представить в виде прямоугольных треугольников или прямоугольников.
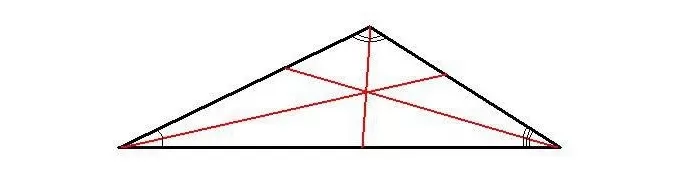
В тупоугольном треугольнике биссектриса делит больший угол на равные части, величина которых меньше 900.
Свойства биссектрисы треугольника
1. Каждая точка этой линии равноудалена от сторон угла. Часто эту характеристику выбирают в качестве определения, поскольку верно и обратное утверждение для любого произвольного треугольника. Это позволяет находить и радиус вписанной окружности.
2. Все внутренние отрезки, делящие углы пополам, пересекаются в одной точке, которая является центром окружности, вписанной в фигуру, т. е. точка пересечения находится на равных расстояниях от сторон.
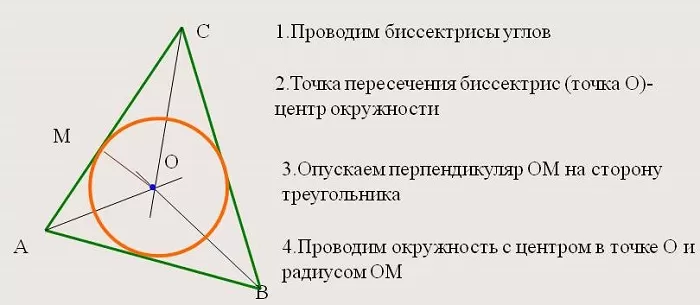
Данное свойство позволяет решать целый класс разнообразных задач, выводить формулы для радиусов вписанных окружностей правильных многоугольников.
Благодаря этому утверждению, легко доказывается следующее правило:
Площадь описанного многоугольника равна:
S = p∗r
где p – полупериметр, а r – радиус вписанной окружности.
Это позволяет находить решение не только планиметрических, но и стереометрических задач.
Важную роль играют внешние биссектрисы треугольника. Вместе с внутренними они образуют прямые углы;
3. Сумма величин двух прилежащих сторон, делённая на длину противолежащей стороны, задаёт отношение частей биссектрисы (считая от вершины), полученных точкой пересечения всех трёх соответствующих линий.
Некоторые виды геометрических фигур, в силу своих особенностей, порождают особые примечательные характеристики;
4. В равнобедренном треугольнике биссектриса, проведённая к основанию, одновременно является медианой и высотой. Две другие – равны между собой.
В этом случае основание параллельно внешней биссектрисе.
Обратное положение также имеет место. Если прямая проведена параллельно основанию равнобедренного треугольника через некоторую вершину, то внешняя биссектриса при этой вершине является частью этой линии;
5. Для равностороннего многоугольника важной характеристикой считается равенство всех биссектрис;
6. У правильного треугольника все внешние биссектрисы параллельны сторонам;
7. Выделяют несколько особенностей, среди которых есть следующая теорема:
«Биссектриса треугольника делит противолежащую сторону на отрезки, пропорциональные двум другим сторонам».
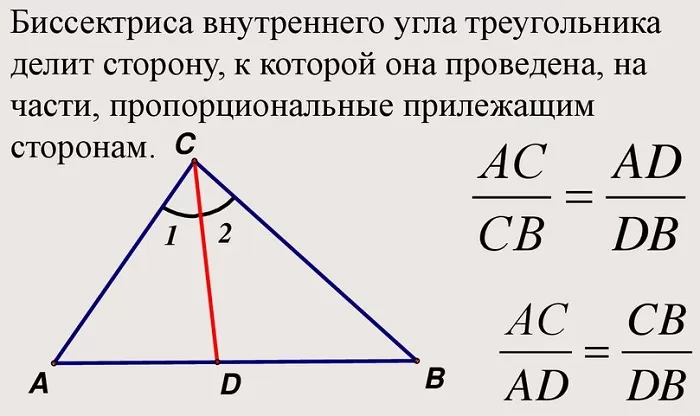
Обратное утверждение («Прямая делит сторону на отрезки, пропорциональные двум другим сторонам») выражает признаки того, что рассматриваемая линия является внутренней биссектрисой;
8. Разносторонний треугольник позволяет определить взаимное расположение его высоты, медианы и биссектрисы, проведённых из одной точки. В частности, медиана и высота располагаются по разные стороны от третьей линии.
Все формулы биссектрисы в треугольнике
В зависимости от исходных данных, длина биссектрисы, проведённой к стороне C, lc, равна:

Примеры решения задач
Задача №1
В ΔABC ∠C = 90°, проведена биссектриса острого угла. Отрезок, соединяющий её основание с точкой пересечения медиан, перпендикулярен катету. Найти углы заданной фигуры.
Решение.
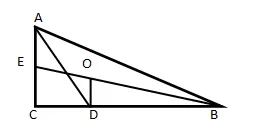
Пусть ∠ACB = 90°, AD – биссектриса, BE – медиана, O – точка пересечения медиан, OD⊥BC.
Тогда OE : OB = 1 : 2по свойству медиан.
Так как OD⊥BC, то ODIIOC, следовательно, ΔBOD ∼ ΔBEC по второму признаку подобия, поэтому, по свойству подобных фигур, CD : DB = 1 : 2.
Это означает, что CA : AB = 1 : 2.
Так как катет равен половине гипотенузы, то ∠ABC = 30°, откуда ∠CAB = 60°.
Ответ: 90°, 60°, 30°.
Задача №2
Диагональ параллелограмма делит его острый угол пополам. Доказать, что этот параллелограмм является ромбом.
Доказательство.

Так как ABCD – параллелограмм, то ∠DAC = ∠ACB, как накрест лежащие при параллельных прямых AD, BC и секущей AC.
По условию, ∠DAC = ∠ACB = ∠BAC, поэтому ΔACB равнобедренный, то есть AB = BC, следовательно, ABCD – ромб.
Доказано.
Источник
Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru. Сегодня мы поговорим о таком термине, как БИССЕКТРИСА.
Это понятие широко применяется в геометрии. И каждый школьник в России знакомится с ним уже в 5 классе. А после эта величина часто используется для решения различных задач.
Биссектриса — это…
Итак,
Биссектриса – это луч, который выходит из вершины треугольника и делит ее ровно на две части.
Также под биссектрисой принято понимать и длину отрезка (что это?), который начинается в вершине треугольника, а заканчивается на противоположной от этой вершины стороне.
Есть еще понятие «биссектриса угла», которая является лучом и точно так же делит угол (любой, не обязательно треугольника) пополам:
Само понятие БИССЕКТРИСА пришло к нам из латинского языка. И название это весьма говорящее. Оно состоит из двух слов – «bi» означает «двойное, пара», а «sectio» можно дословно перевести, как «разрезать, поделить».
Вот и получается, что само слово БИССЕКТРИСА – это «разрезание пополам», что собственно и отражается в определении термина, который мы только что привели.
А сейчас задачка на закрепление материала. Посмотрите на эти рисунки и скажите, на каком изображена биссектриса. Подумали? Правильно, на втором.
На первом луч, выходящий из угла АОВ, явно не делит его пополам. На втором это соотношение углов более очевидно, а потому можно предположить, что луч ОД является БИССЕКТРИСОЙ. Хотя, конечно, на сто процентов это утверждать сложно.
Для более точного определения используют специальные инструменты. Например, транспортир. Это такой инструмент в виде полусферы из металла или пластмассы. Вот как он выглядит:
Хотя есть еще вот такие варианты:
Наверняка у каждого такие были в школе. И пользоваться ими весьма просто. Надо только ровненько совместить основание транспортира (прямоугольная линейка) с основанием треугольника, а после на полусфере отметить значение, которое соответствует размеру угла.
И точно по такой же схеме можно поступить наоборот – имея транспортир, начертить угол необходимого размера. Чаще всего – от 0 до 180 градусов. Но на втором рисунке у нас транспортир, который помогает начертить градусы от 0 до 360.
Количество биссектрис в треугольнике
Но вернемся к нашей главной теме. И ответим на вопрос – сколько БИССЕКТРИС есть в треугольнике?
Ответ в общем-то логичен, и он заложен в самом названии нашей геометрической фигуры. Треугольник – три угла. А соответственно, и биссектрис в нем будет тоже три – по одной на каждую вершину.
Снова посмотрим на наши рисунки. В данном случае наглядно видно, что у треугольника АВС (именно так в геометрии обозначается эта фигура – по наименованию ее вершин) три БИССЕКТРИСЫ. Это отрезки AD, BE и CF.
На чертежах БИССЕКТРИСЫ обозначатся следующим образом. Видите одинарные выгнутые черточки между отрезками АС /AL1 и АВ/AL1? Так обозначаются углы. А то, что они оба обозначены одинаковыми черточками, говорит о том, что углы равны. А значит, отрезок AL1 является БИССЕКТРИСОЙ.
То же самое относится и к углам между АВ/DL2 и ВС/BL2. Они обозначены одинаковыми двойными черточками. А значит, отрезок BL2 – биссектриса. А углы АС/CL3 и ВС/CL3 обозначены тройными черточками. Соответственно, это показывает, что отрезок CL3 также является биссектрисой.
Пересечение биссектрис треугольника
Как можно было заметить по приведенным выше рисункам, у биссектрис треугольника есть одно важное свойство. А именно:
Биссектрисы треугольника всегда пересекаются в одной точке, называемой инцентром!
Это правило является аксиомой (что это такое?) и не допускает никаких исключений. Другими словами, вот такого быть не может:
Если вы видите такую картину, то перед вами точно не БИССЕКТРИСЫ. Во всяком случае, минимум один отрезок таковой не является. А может и все три.
А есть еще один интересный факт, связанный с пересечением биссектрис треугольника.
Центр пересечения биссектрис в треугольнике является центром окружности, который списан в эту фигуру.
Это свойство биссектрис на самом деле не только выглядит интересно на чертежах. Оно часто помогает в решение сложных задач.
Свойство основания биссектрисы
У каждой БИССЕКТРИСЫ есть основание. Так называют точку пересечения со стороной треугольника. Например, в нашем случае это будет точка К.
И с этим основанием связана одна весьма интересная теорема. Она гласит, что
Биссектриса треугольника делит противоположную сторону, то есть точкой основания, на два отрезка. И их отношение равно отношению двух прилежащих сторон.
Звучит несколько тяжеловато, но на деле выглядит весьма просто. Отношение отрезков на основании биссектрисы – это ВК/КС. А отношение прилежащих сторон – это АВ/АС. И получается, что в нашем случае теорема выглядит вот так:
ВК/КС = АВ/АС
Интересно, что для данной теоремы будет справедливо и другое утверждение:
ВК/АВ = КС/АС
Ну, как часто бывает в математике – это правило работает и в обратном направлении. То есть, если вы знаете длины все сторон и их соотношения равны, то можно сделать вывод, что перед нами БИССЕКТРИСА, А соответственно, будет проще рассчитать размер угла треугольника.
Биссектриса равнобедренного треугольника
Для начала напомним, что такое равнобедренный треугольник.
Это такой треугольник, у которого две стороны абсолютно равны (то есть имеет равные «бедра»).
Так вот в таком треугольнике БИССЕКТРИСА имеет весьма интересные свойства.
Она одновременно является еще и медианой (что это?), и высотой.
Эти понятия нам также знакомы по школьному курсу. Но если кто забыл, мы обязательно напомним:
- Высота – линия, которая выходит из вершины треугольника и опускается на противоположную сторону под прямым углом.
- Медиана – линия, которая выходит из вершины треугольника, и делит противоположную сторону на две ровные части.
А в равностороннем треугольнике или как его еще называют правильном (у которого все стороны и все углы равны) все три биссектрисы являются высотами и медианами. И плюс ко всему, их длины равны.
Вот и все, что нужно знать о таком понятии, как БИССЕКТРИСА. До новых встреч на страницах нашего блога.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Использую для заработка
- ВоркЗилла – удаленная работа для всех
- Анкетка – платят за прохождение тестов
- Etxt – платят за написание текстов
- Кьюкоммент – биржа комментариев
- Поиск лучшего курса обмена
- 60сек – выгодный обмен криптовалют
- Бинанс – надёжная биржа криптовалют
- ВкТаргет – заработок в соцсетях (ВК, ОК, FB и др.)
Источник
Биссектриса треугольника – это уникальный отрезок; он один из самых сложных по восприятию и пониманию. Легко понять и осознать, что такое высота, можно разобраться с определением и назначением медианы, но биссектрисы – это сложно. Просто потому, что основой для понимания биссектрисы служит понимание угла, а это не так легко усвоить, как величину отрезка.

Определения
Какие определения нам понадобятся в процессе работы? Во-первых, это определение биссектрисы.
Биссектриса – это луч, имеющий начало в вершине угла и делящий угол пополам.
Биссектриса треугольника – это отрезок биссектрисы, которой начинается в вершине треугольника и заканчивается на стороне, противолежащей этой вершине.
Вписанная окружность – это окружность, которая касается всех сторон треугольника. Треугольник в этом случае называется описанным.
Теперь обозначим основные свойства биссектрисы и приведем для них доказательства.
Первое, что нужно обозначить, это различие понятий биссектрисы и биссектрисы треугольника. Это похожие вещи, но свойства биссектрис углов треугольников не будут действовать на все биссектрисы. Это нужно запомнить.
Свойства биссектрисы треугольника
- Биссектриса в треугольнике делит сторону на отрезки, пропорциональные прилежащим сторонам.
Проведем в треугольнике АВС биссектрису ВК. После этого проведем прямую СМ, параллельную этой биссектрисе так, что точка М будет являться точкой пересечения продолжения стороны АВ.
Тогда два параллельных отрезка ВК и МС отсекут от сторон угла ВАС пропорциональные отрезки. То есть: АВ:АК=ВМ:КС. Докажем, что ВМ=ВС. Для этого посмотрим на треугольник ВМС. Угол АВК равен углу ВМС, как соответственные углы параллельных прямых при секущей АМ. С другой стороны угол КВС равен углу ВСМ, как накрест лежащие при параллельных прямых и секущей ВС. Но при этом угол АВК равен углу КВС, так как ВК – это биссектриса. Запишем все в виде равенств для большего понимания.
$$АВК = ВМС$$
$$КВС = ВСМ$$
$АВК = КВС$, значит углы ВМС и МСВ равны, а треугольник МВС – равнобедренный. Тогда $ВМ=ВС$ и $АВ:АК=ВС:СК$. Что и требовалось доказать.
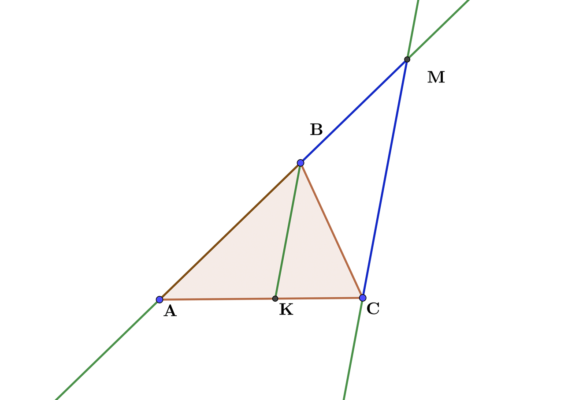
Рис. 1. Первое свойство
- Биссектриса равноудалена от сторон угла, в котором она проведена.
Это свойство не биссектрисы треугольника, а любой биссектрисы, поэтому ее доказательство проще рассматривать на рисунке угла.
Нарисуем угол АВС и проведем в нем биссектрису ВМ. Расстояние от биссектрисы до стороны в любой точке это перпендикуляр. Поэтому выберем произвольную точку на биссектрисе. Назовем ее D и опустим перпендикуляр на сторону АВ в точку Р и на сторону ВС в точку N. Тогда мы получим два прямоугольных треугольника: DРВ и DNB, равные между собой по гипотенузе ВD, которая будет общей стороной треугольников, и острому углу, так как угол PBD равен углу DBN, так как ВМ – биссектриса. Значит, и стороны PD=DN – как соответственные элементы. Доказательство простое, но изящное. Знание этого свойство поможет в доказательстве следующей теоремы.
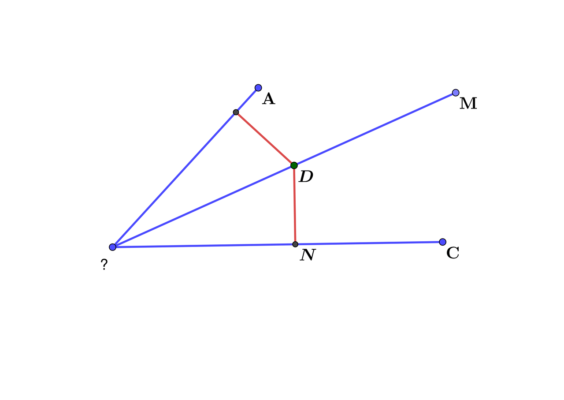
Рис. 2. Второе свойство
- Биссектрисы треугольника пересекаются в одной точке, и эта точка служит центром вписанной окружности. Это доказывается очень просто, необходимо из точки пересечения опустить перпендикуляры к каждой стороне.
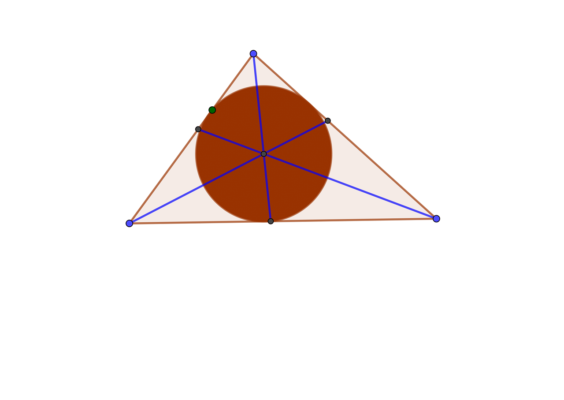
Рис. 3. Третье свойство
Что мы узнали?
Мы узнали, что такое биссектриса треугольника и чем она отличается от обычной биссектрисы. Выделили три свойства биссектрисы треугольника, которые пригодятся при решении задач и доказательстве теорем.
Тест по теме
Оценка статьи
Средняя оценка: 3.9. Всего получено оценок: 191.
Источник
