Каким свойством обладает биссектриса равнобедренного треугольника
Биссектриса равнобедренного треугольника обладает особенным свойством, которое определяет стиль решения задач на нахождение элементов равнобедренного треугольника. Чтобы лучше понять смысл решения подобных задач, поговорим о биссектрисе равнобедренного треугольника.

Определения
Равнобедренный треугольник – это треугольник, две стороны которого равны между собой. Третья сторона зовется основанием, углы при основании равны.
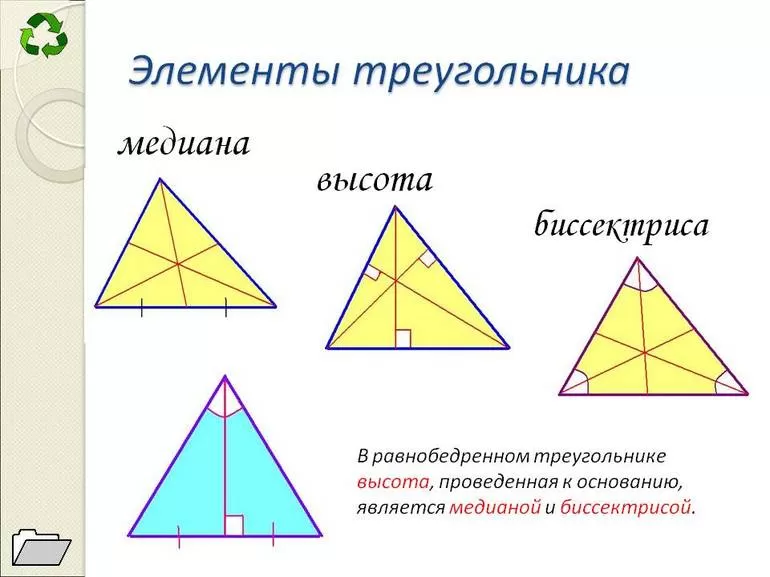
Биссектриса треугольника – это отрезок, который делить угол треугольника на две равные части. Каждая точка биссектрисы равноудалена от каждой из сторон треугольника, т.е. если из любой точки биссектрисы опустить перпендикуляры на каждую из сторон угла, то эти перпендикуляры окажутся равны между собой. Точка пересечения биссектрис является центром вписанной в треугольник окружности и зовется инцентром треугольника.

Рис. 1. Биссектриса
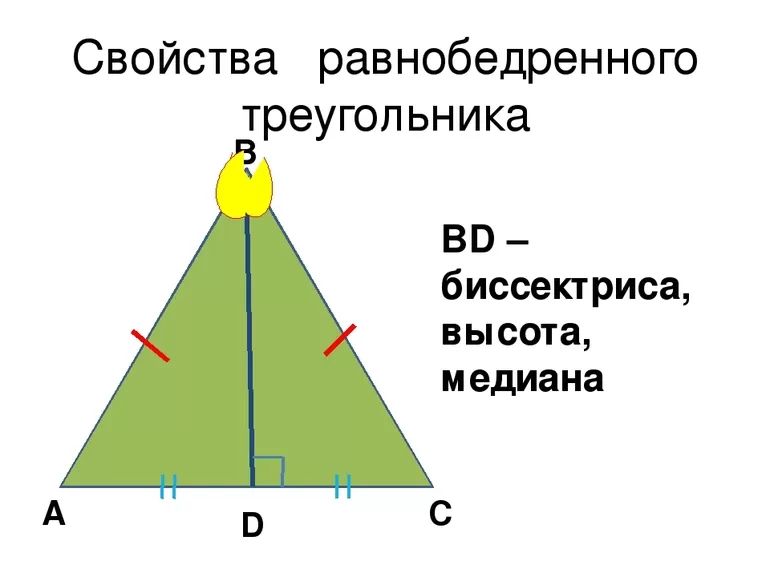
Биссектриса равнобедренного треугольника
Равнобедренный треугольник уникален равенством двух сторон и двух углов. Именно этим обеспечивается основное свойство биссектрисы равнобедренного треугольника: в равнобедренном треугольнике биссектриса, проведенная к основанию, совпадает с высотой и медианой.
В равнобедренному треугольнике только биссектриса, проведенная к основанию, совпадает с высотой и медианой. Две другие биссектрисы будут разница с соответствующими медианами и высотами. Это стоит запомнить раз и навсегда, чтобы не допускать нелепых ошибок.
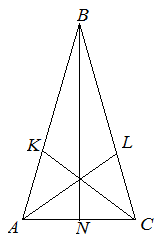
Рис. 2. Биссектрисы в равнобедренном треугольнике
При решении задач, нужно понимать, что это свойство можно применять не только в равнобедренном, но и в равностороннем треугольнике.
Ведь, если выбрать любую из сторон равностороннего треугольника и принять ее за основание, то две другие стороны будут равны, а, значит, равносторонний треугольник может считаться равнобедренным треугольником, у которого любая сторона может выступать в роли основания.
А раз любую сторону можно принимать за основание, то и каждая биссектриса будет совпадать с каждой соответствующей медианой и высотой. Ведь каждая биссектриса будет проведена к стороне, которую можно считать основанием.
Именно на этом свойстве основано равенство двух треугольников, которые получаются в равнобедренном треугольнике в результате проведения биссектрисы. Ведь в таких треугольниках одна сторона, та самая биссектриса, будет общей.
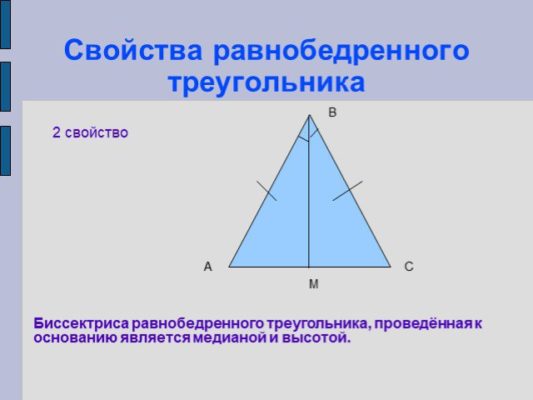
Рис. 3. Биссектриса проведенная к основанию равнобедренного треугольника
Биссектриса совпадет с высотой, а, значит, два малых треугольника будут прямоугольными, а биссектриса дает два равных угла. То есть, два треугольника будут равны по катету и прилежащему острому углу, одному из признаков равенства прямоугольных треугольников.
Использование двух малых треугольников часто встречается на практике. Например, если известно основание треугольника и его боковая сторона, а нужно найти биссектрису, сделать это можно гораздо проще, нежели в других треугольниках.
Биссектриса совпадет с медианой и высотой, а, значит, станет катетом малого прямоугольного треугольника, тогда значение биссектрисы можно найти как значение катета через теорему Пифагора.
Что мы узнали?
Мы вспомнили, что такое равнобедренный треугольник. Поговорили о свойствах биссектрисы равнобедренного треугольника, в особенности остановившись на свойствах биссектрисы равнобедренного треугольника и равностороннего треугольника. Выделили наиболее применяемый и простой способ нахождения биссектрисы равнобедренного треугольника.
Тест по теме
Доска почёта
Чтобы попасть сюда – пройдите тест.
-
Анастасия Уманец
9/10
Оценка статьи
Средняя оценка: 4.6. Всего получено оценок: 100.
Источник
Содержание:
- Свойства равнобедренного треугольника.
- Признаки равнобедренного треугольника.
- Формулы равнобедренного треугольника:
- формулы длины стороны;
- формулы длины равных сторон;
- формулы высоты, медианы, биссектрисы равнобедренного треугольника.
Равнобедренным называется треугольник, у которого две стороны равны. Эти стороны называются боковыми, а третья сторона — основанием.
АВ = ВС — боковые стороны
АС — основание
Свойства равнобедренного треугольника
Свойства равнобедренного треугольника выражаются через 5 теорем:
Теорема 1. В равнобедренном треугольнике углы при основании равны.
Доказательство теоремы:
Рассмотрим равнобедренный Δ ABC с основанием АС.
Боковые стороны равны АВ = ВС,
Следовательно углы при основании ∠ BАC = ∠ BСA.
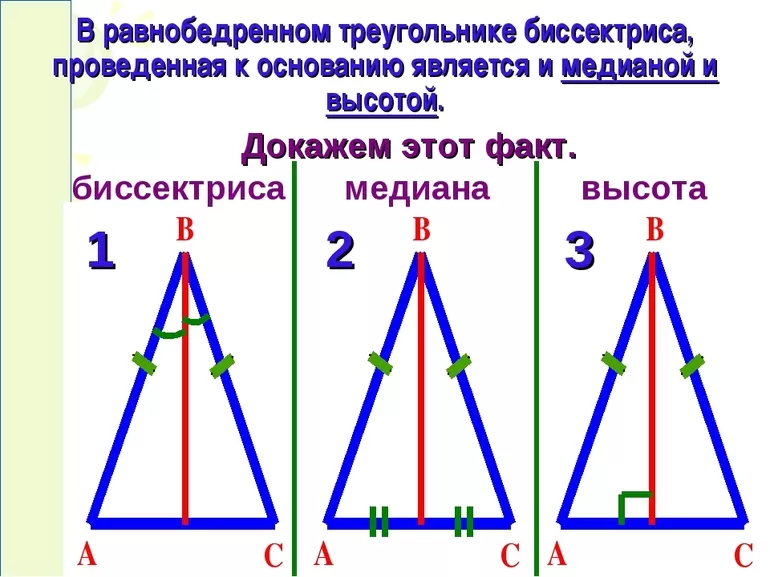
Теорема о биссектрисе, медиане, высоте, проведенной к основанию равнобедренного треугольника
- Теорема 2. В равнобедренном треугольнике биссектриса, проведенная к основанию, является медианой и высотой.
- Теорема 3. В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
- Теорема 4. В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
Доказательство теоремы:
- Дан Δ ABC.
- Из точки В проведем высоту BD.
- Треугольник разделился на Δ ABD и ΔCBD. Эти треугольники равны, т.к. гипотенузы и общий катет у них равны (теорема Пифагора).
- Прямые АС и BD называются перпендикуляром.
- В Δ ABD и Δ BCD ∠ BАD = ∠ BСD (из Теоремы 1).
- АВ = ВС — боковые стороны равны.
- Стороны АD = СD, т.к. точка D отрезок делит пополам.
- Следовательно Δ ABD = ΔBCD.
- Биссектриса, высота и медиана это один отрезок – BD
Вывод:
- Высота равнобедренного треугольника, проведенная к основанию, является медианой и биссектрисой.
- Медиана равнобедренного треугольника, проведенная к основанию, является высотой и биссектрисой.
- Биссектриса равнобедренного треугольника, проведенная к основанию, является медианой и высотой.
Запомни! При решении таких задач опусти высоту на основание равнобедренного треугольника. Чтобы разделить его на два равных прямоугольных треугольника.
- Теорема 5. Если три стороны одного треугольника равны трем сторонам другого треугольника, то такие треугольники равны.
Доказательство теоремы:
Дано два Δ ABC и Δ A1B1C1. Стороны AB = A1B1; BC = B1C1; AC = A1C1.
Доказательство от противного.
- Пусть треугольники не равны (а то треугольники были равны по первому признаку).
- Пусть Δ A1B1C2 = Δ ABC, у которого вершина C2 лежит в одной полуплоскости с вершиной C1 относительно прямой A1B1. По предположению вершины C1 и C2 не совпадают. Пусть D – середина отрезка C1C2. Δ A1C1C2 и Δ B1C1C2 – равнобедренные с общим основанием C1C2. Поэтому их медианы A1D и B1D являются высотами. Значит, прямые A1D и B1D перпендикулярны прямой C1C2. A1D и B1D имеют разные точки A1 и B1, следовательно, не совпадают. Но через точку D прямой C1C2 можно провести только одну перпендикулярную ей прямую.
- Отсюда пришли к противоречию и теорему доказали.
Признаки равнобедренного треугольника
- Если в треугольнике два угла равны.
- Сумма углов треугольника 180°.
- Если в треугольнике биссектриса является медианой или высотой.
- Если в треугольнике медиана является биссектрисой или высотой.
- Если в треугольнике высота является медианой или биссектрисой.
Формулы равнобедренного треугольника
Формулы сторон равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы длины стороны (основания — b):
- b = 2a sin( beta /2)= a sqrt { 2-2 cos beta }
- b = 2a cos alpha
Формулы длины равных сторон — (а):
- a=frac { b } { 2 sin(beta /2) } = frac { b } { sqrt { 2-2 cos beta } }
- a=frac { b } { 2 cosalpha }
Формулы высоты, медианы, биссектрисы равнобедренного треугольника
- L — высота=биссектриса=медиана
- b — сторона (основание)
- а — равные стороны
- a — углы при основании
- b — угол образованный равными сторонами
Формулы высоты, биссектрисы и медианы, через сторону и угол, (L):
- L = a sina
- L = frac { b } { 2 } *tgalpha
- L = a sqrt { (1 + cos beta)/2 } =a cos (beta)/2)
Формула высоты, биссектрисы и медианы, через стороны, (L):
- L = sqrt { a^ { 2 } -b^ { 2 } /4 }
Площадь равнобедренного треугольника
- b — сторона (основание)
- а — равные стороны
- h — высота
Формула площади треугольника через высоту h и основание b, (S):
S=frac { 1 } { 2 } *bh
Смотри также:
- Теорема о сумме углов треугольника
- Формулы площади поверхности, основания, сечения призмы
- Площадь поверхности куба, формулы и примеры
- Основные формулы по математике
- Справочные материалы ЕГЭ от ФИПИ по математике
Источник
Общие сведения
Геометрическая фигура является треугольником, если она состоит из трех точек, лежащих в одной плоскости и не лежащих на одной прямой. Она изучается в пятом классе. В геометрии принято сокращенное обозначение при помощи символа Δ, после которого следует писать произвольные три литеры (вершины) в алфавитном порядке. Например, ТUV.
Вершина — точка, из которой исходят два отрезка и образуют две стороны. Отрезок является элементом луча. Обозначается он двумя заглавными литерами (ТU, UV и т. д. ). Луч — часть прямой, имеющая только начало. Он необходим для построения отрезков, из которых состоят все фигуры геометрии.
Прямая — линия, проходящая в бесконечном пространстве. У нее не существует начала и конца. Математики обозначают ее произвольной маленькой латинской буквой (например, m). Кроме того, у равнобедренного Δ существуют и дополнительные параметры — биссектриса, медиана и высота. Первая делит любой угол (сокращенное обозначение — ∠) при вершине, из которой она исходит, на два ∠ с эквивалентной градусной мерой, т. е. пополам.
Медиана соединяет вершину и середину противоположной стороны, а высота — простой перпендикуляр. Он начинается в вершине и находится внутри треугольника, опускаясь на противолежащую сторону.
Равнобедренный Δ – фигура, имеющая две равные боковые стороны. Следует отметить, что любая биссектриса равнобедренного треугольника является медианой. Это правило выполняется, когда она проведена к основанию фигуры. Существует еще один вид Δ. Он называется правильным или равносторонним. Для него справедливо такое утверждение, сформулированное учеными-математиками: любая высота является медианой и биссектрисой. Для решения задач по геометрии рекомендуется знать теорему о биссектрисе равнобедренного треугольника и ее свойства.
Теоремы о биссектрисах
Теорема о биссектрисах треугольника звучит таким образом: точка пересечения биссектрис — инцентр ΔTUV. Доказывается теорема по такому алгоритму:

- Из вершин T и U нужно провести биссектрисы TT’ и UU’ на противоположные стороны UV и TV соответственно.
- На чертеже видно, что они пересекаются в некоторой точке. Последнюю следует обозначить Z.
- Если предположить, что TT’ и UU’ не пересекаются, а параллельны (||), то секущей является сторона TU. В этом случае должно выполняться тождество: ∠(Т/2)+∠(U/2)=180.
- Однако утверждение в третьем пункте противоречит сумме градусных мер ∠ треугольника, поскольку ∠Т+∠U+∠V=180. Из выражения, полученного на третьем шаге алгоритма, следует, что ∠Т+∠U=360.
- На основании рассуждений можно сделать вывод, что Z — точка пересечения биссектрис.
- Таким же образом доказывается случай для вершины V и биссектрисы VV’.
- Точка Z — центр описанной окружности. Чтобы это доказать, нужно просто провести круг. На рисунке все вершины ΔTUV будут лежать на нем. Теорема полностью доказана.
Кроме того, существует еще одно утверждение, имеющее такой вид: любая высота равнобедренного треугольника является его биссектрисой и медианой.
Доказать его можно посредством такой методики:
- Начертить равнобедренный ΔTUV. У него стороны TU=UV, а TV — основание.
- Провести высоту UU’ на основание.
- Рассмотреть два прямоугольный Δ: TUU’ и UVU’. Они равны между собой, поскольку UU’ — общая, TU=UV и углы (∠Т=∠V) при основании — по определению равнобедренного Δ, а ∠ТU’U=∠UU’V — по построению.
- На основании третьего пункта можно сделать вывод о равенстве сторон TU’ и VU’, а также ∠U’UТ=∠VU’U. Следовательно, в первом случае UU’ — медиана, а во втором — биссектриса.
- На основании четвертого утверждения теорема доказана.
Кроме того, существуют определенные свойства, которые могут быть полезными при решении задач. Их получают из теорем и других тождеств, доказываемые математиками.
Полезные свойства
Математики вывели пять полезных свойств для биссектрисы в равнобедренном Δ.
К ним относятся следующие:
- Свойство биссектрисы, проведенной к основанию равнобедренного треугольника: она есть медиана и высота.
- При проведении из вершин, образующих основание, углы, образованные ими, эквивалентны между собой.
- Если провести биссектрису TT’ из вершины при основании, то будет выполняться следующее тождество: TU/TV=UT’/T’V (отношение стороны к основанию эквивалентно частному из двух отрезков, полученных при построении).
- Длина биссектрисы, проведенной к основанию, эквивалентна корню второй степени из квадрата боковой стороны без четвертой части квадрата основания: UU’=[m 2 — (¼)*n 2 ](^½), где m и n — длина боковой стороны и основания.
- Через точку пересечения проходит круг, касающийся вершин основания.
Следует отметить, что в равностороннем треугольнике каждая биссектриса будет отсекать равные углы из каждой вершины.
В нем можно провести их всего три, а в равнобедренном — 2 высоты, 2 медианы, 2 биссектрисы, а также одну к основанию.
Пример решения
Чтобы усвоить материал, необходимо решить задачу по геометрии. Ее условие имеет такой вид:
- Периметр равнобедренного Δ равен 40 см.
- Основание больше боковой стороны на 10 см.
Необходимо найти значение высоты. Решать нужно по такому алгоритму:
- Составить уравнение: 40=2*t+(t+10), где t — боковая сторона, а (t+10) — основание.
- Раскрыть скобки: 40=2*t+t+10.
- Привести подобные коэффициенты:3t=30.
- Найти неизвестную: t=10 (см).
- Вычислить основание: 10+10=20 (см).
- Определить высоту: h= [100+((¼)*20)^2]^(½)=5[5]^(½) (см).
Следовательно, высота равнобедренного Δ со сторонами 10 и 20 см эквивалентна 5[5]^(½) см. Существуют и более сложные задачи, в которых требуется составлять уравнения. Например, условие одной из них имеет такой вид:
- Высота, опущенная из вершины на основание (ТТ’), равна 20 см.
- Основание больше стороны на 5 см.
Необходимо найти периметр треугольника. Для решения задачи необходимо составить определенный алгоритм:
- Обозначить стороны: основание — n, сторона — m и высота — h.
- Периметр P: Р=2m+n.
- Записать формулу, руководствуясь первым и четвертым свойствами биссектрисы: h=[m 2 -(¼)*n 2 ]^(½).
- Записать связь сторон, обозначив боковую сторону переменной t: t=t+5.
- Подставить в соотношение во втором пункте: 20=[t 2 -(¼)*(t+5)^2]^(½).
- Возвести обе части в квадрат: 400=t 2 -(¼)*(t+5)^2.
- Раскрыть скобки: 400=t 2 -(¼)*(t 2 +10+25)=t 2 -(¼)t 2 −10/4−25/4=(¾)t 2 -(10/4)-25/4=(¼)*(3t 2 -10−25).
- Решить квадратное уравнение, сократив на ¼ обе части: (3t 2 -10t-25)=200.
- Первый корень равен -7, а второй — +25. Второе значение подходит, поскольку является положительным числом.
- Основание вычисляется таким образом: n=25+5=30 (см).
- Если подставить полученное значение для проверки в соотношение h=[t 2 -(¼)*(t+5)^2]^(½), то получится такое выражение: 20=[25 2 -(¼)*30 2 ]^(½)=[625−900/4]^(½)=[625−225]^(½)=20. Значение найдено верно.
- Периметр находится по формуле: P=25*2+30=80 (см).
Задача решена в полном объеме. Из методики решения видно, что сначала нужно записать основную формулу, а затем найти неизвестные в ней величины по другим вспомогательным тождествам.
Таким образом, при решении задач по геометрии необходимо знать основные определения, формулы, свойства и теоремы, которые также могут быть полезны.
Источник
Определения
Медиана треугольника – это отрезок, соединяющий вершину треугольника с серединой противоположной стороны.
Биссектриса треугольника – это отрезок биссектрисы угла треугольника, соединяющий вершину треугольника с точкой противоположной стороны.
Высота треугольника – это перпендикуляр, проведенный из вершины треугольника к прямой, содержащей противоположную сторону.
Теорема
В любом треугольнике высоты (или их продолжения) пересекаются в одной точке (рис. 1 и 2), биссектрисы пересекаются в одной точке (рис. 3), медианы пересекаются в одной точке (рис. 4).

Теорема
В равнобедренном треугольнике биссектриса, проведённая к основанию, является медианой и высотой.

Верны и другие утверждения:
В равнобедренном треугольнике высота, проведенная к основанию, является биссектрисой и медианой.
В равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой.
[{Large{text{Медиана}}}]
Теорема
В любом треугольнике медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Доказательство
Пусть (AD) и (BE) – медианы в треугольнике (ABC), (O) – точка пересечения (AD) и (BE).

(DE) – средняя линия в треугольнике (ABC), тогда (DEparallel AB), значит (angle ADE = angle BAD), (angle BED = angle ABE), следовательно, треугольники (ABO) и (DOE) подобны (по двум углам).
Из подобия треугольников (ABO) и (DOE): (dfrac{BO}{OE} =
dfrac{AB}{DE} = dfrac{2}{1}).
Для других медиан треугольника (ABC) требуемое свойство доказывается аналогично.
Теорема
Медиана треугольника делит его на два равновеликих треугольника (равновеликие треугольники – это треугольники, у которых площади равны).
Доказательство
Площадь треугольника равна половине произведения основания на высоту, проведенную к этому основанию: (S_{ABC} = 0,5cdot ACcdot
h).

Пусть (BD) – медиана в треугольнике (ABC), тогда (AD = DC).
(S_{ABD} = 0,5cdot ADcdot h),
(S_{BCD} = 0,5cdot DCcdot h).
Так как (AD = DC), то (S_{ABD} = S_{BCD}), что и требовалось доказать.
Теорема
В прямоугольном треугольнике медиана, проведенная к гипотенузе, равна половине гипотенузы.
Верно и обратное: если медиана равна половине стороны, к которой она проведена, то она проведена из вершины прямого угла.
Доказательство
1) Докажем, что если (triangle ABC) – прямоугольный, то (BM=frac12AC), где (M) – середина гипотенузы (AC).

Достроим треугольник (ABC) до прямоугольника (ABCD) и проведем диагональ (BD). Т.к. в прямоугольнике диагонали делятся точкой пересечения пополам и равны, то (ACcap BD=M), причем (AM=MC=BM=MD), чтд.
2) Докажем, что если в треугольнике (ABC) медиана (BM=AM=MC), то (angle B=90^circ).

Треугольники (AMB) и (CMB) – равнобедренные, следовательно, (angle
BAM=angle ABM=alpha, quad angle MBC=angle MCB=beta).
Т.к. сумма углов в треугольнике равна (180^circ), то для (triangle
ABC):
(alpha+(alpha+beta)+beta=180^circ Rightarrow
alpha+beta=90^circ Rightarrow angle B=90^circ), чтд.
[{Large{text{Биссектриса}}}]
Теорема
Биссектриса треугольника делит его сторону на части, пропорциональные прилежащим сторонам:

Верно и обратное: если отрезок, проведенный из вершины треугольника к стороне, делит эту сторону на отрезки, пропорциональные прилежащим сторонам, то это биссектриса.
Доказательство
Площади треугольников, у которых есть равные углы, относятся как произведения сторон, образующих эти углы, то есть [dfrac{S_{ACD}}{S_{BCD}} = dfrac{ACcdot CD}{CBcdot CD} =
dfrac{AC}{CB}]
С другой стороны, (dfrac{S_{ACD}}{S_{BCD}} = dfrac{0,5cdot
ADcdot h}{0,5cdot DBcdot h}), где (h) – высота, проведённая из точки (C), тогда (dfrac{S_{ACD}}{S_{BCD}} = dfrac{AD}{DB}).
В итоге (dfrac{AD}{DB} = dfrac{S_{ACD}}{S_{BCD}} =
dfrac{AC}{CB}), откуда (dfrac{AD}{AC} = dfrac{DB}{BC}), что и требовалось доказать.
Теорема
Если точка равноудалена от сторон угла, то она лежит на его биссектрисе.
Верно и обратное: если точка лежит на биссектрисе угла, то она равноудалена от его сторон.

Доказательство
1) Докажем, что если (KA=KB), то (OK) – биссектриса.
Рассмотрим треугольники (AOK) и (BOK): они равны по катету и гипотенузе, следовательно, (angle AOK=angle BOK), чтд.
2) Докажем, что если (OK) – биссектриса, то (KA=KB).
Аналогично треугольники (AOK) и (BOK) равны по гипотенузе и острому углу, следовательно, (KA=KB), чтд.
Источник
