Каким свойством должны обладать кролики фибоначчи

Вам, конечно же, знакома идея о том, что математика является самой главной из всех наук. Но многие могут с этим не согласиться, т.к. порой кажется, что математика – это лишь задачи, примеры и тому подобная скукотища. Однако математика может запросто показать нам знакомые вещи с совершенно незнакомой стороны. Мало того – она даже может раскрыть тайны мироздания. Как? Давайте обратимся к числам Фибоначчи.
Что такое числа Фибоначчи?
Числа Фибоначчи являются элементами числовой последовательности, где каждое последующее число образуется посредством суммирования двух предыдущих, например: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89… Как правило, записывается такая последовательность формулой: F0 = 0, F1 = 1, Fn = Fn-1 + Fn-2, n ≥ 2.
Числа Фибоначчи могут начинаться и с отрицательных значений «n», но в таком случае последовательность будет двусторонней – она будет охватывать и положительные и отрицательные числа, стремясь к бесконечности в двух направлениях. Примером такой последовательности может послужить: -34, -21, -13, -8, -5, -3, -2, -1, 1, 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, а формула будет: Fn = Fn+1 — Fn+2 или же F-n = (-1)n+1Fn.
Создателем чисел Фибоначчи является один из первых математиков Европы средних веков по имени Леонардо Пизанский, которого, собственно и знают, как Фибоначчи – это прозвище он получил спустя много лет после своей смерти.
При жизни Леонардо Пизанский очень любил математические турниры, по причине чего в своих работах («Liber abaci» /«Книга абака», 1202; «Practica geometriae»/«Практика геометрии», 1220, «Flos»/«Цветок», 1225 год – исследование на тему кубических уравнений и «Liber quadratorum»/«Книга квадратов», 1225 – задачи о неопределенных квадратных уравнениях) очень часто разбирал всевозможные математические задачи.
О жизненном пути самого Фибоначчи известно крайне мало. Но достоверно известно то, что его задачи пользовались огромнейшей популярностью в математических кругах в последующие века. Одну из таких мы и рассмотрим далее.
Задача Фибоначчи с кроликами
Для выполнения задачи автором были поставлены следующие условия: есть пара новорождённых крольчат (самка и самец), отличающихся интересной особенностью – со второго месяца жизни они производят новую пару кроликов – тоже самку и самца. Кролики находятся в замкнутом пространстве и постоянно размножаются. И ни один кролик не умирает.
Задача: определить количество кроликов через год.
Решение:
У нас есть:
- Одна пара кроликов в начале первого месяца, которая спаривается в конце месяца
- Две пары кроликов во втором месяце (первая пара и потомство)
- Три пары кроликов в третьем месяце (первая пара, потомство первой пары с прошлого месяца и новое потомство)
- Пять пар кроликов в четвёртом месяце (первая пара, первое и второе потомство первой пары, третье потомство первой пары и первое потомство второй пары)
Количество кроликов в месяц «n» = количеству кроликов прошлого месяца + количество новых пар кроликов, другими словами, вышеназванная формула: Fn = Fn-1 + Fn-2. Отсюда получается рекуррентная числовая последовательность (о рекурсии мы скажем далее), где каждое новое число соответствует сумме двух предыдущих чисел:
1 месяц: 1 + 1 = 2
2 месяц: 2 + 1 = 3
3 месяц: 3 + 2 = 5
4 месяц: 5 + 3 = 8
5 месяц: 8 + 5 = 13
6 месяц: 13 + 8 = 21
7 месяц: 21 + 13 = 34
8 месяц: 34 + 21 = 55
9 месяц: 55 + 34 = 89
10 месяц: 89 + 55 = 144
11 месяц: 144 + 89 = 233
12 месяц: 233+ 144 = 377
И эта последовательность может продолжаться бесконечно долго, но учитывая, что задачей является узнать количество кроликов по истечении года, получается 377 пар.
Здесь важно также заметить, что одним из свойств чисел Фибоначчи является то, что если сопоставить две последовательные пары, а затем разделить большую на меньшую, то результат будет двигаться по направлению к золотому сечению, о котором мы также скажем ниже.
Пока же предлагаем вам ещё две задачи по числам Фибоначчи:
- Определить квадратное число, о котором известно только, что если отнять от него 5 или прибавить к нему 5, то снова выйдет квадратное число.
- Определить число, делящееся на 7, но при условии, что поделив его на 2, 3, 4, 5 или 6 в остатке будет 1.
Такие задачи не только станут отличным способом развития ума, но и занимательным времяпрепровождением. О том, как решаются эти задачи, вы также можете узнать, поискав информацию в Интернете. Мы же не будем заострять на них внимание, а продолжим наш рассказ.
Что же такое рекурсия и золотое сечение?
Рекурсия
Рекурсия является описанием, определением или изображением какого-либо объекта или процесса, в котором есть сам данный объект или процесс. Иначе говоря, объект или процесс можно назвать частью самого себя.
Рекурсия широко используется не только в математической науке, но также и в информатике, массовой культуре и искусстве. Применимо к числам Фибоначчи, можно сказать, что если число равно «n>2», то «n» = (n-1)+(n-2).
Золотое сечение
Золотое сечение является делением целого на части, соотносящиеся по принципу: большее относится к меньшему аналогично тому, как общая величина относится к большей части.
Впервые о золотом сечении упоминает Евклид (трактат «Начала» прим. 300 лет до н.э.), говоря и построении правильного прямоугольника. Однако более привычное понятие было введено немецким математиком Мартином Омом.
Приблизительно золотое сечение можно представить в качестве пропорционального деления на две разные части, к примеру, на 38% и 68%. Численное же выражение золотого сечения равно примерно 1,6180339887.
На практике золотое сечение используется в архитектуре, изобразительном искусстве (посмотрите работы Леонардо да Винчи), кино и других направлениях. На протяжении долгого времени, впрочем, как и сейчас, золотое сечение считалось эстетической пропорцией, хотя большинством людей оно воспринимается непропорциональным – вытянутым.
Вы можете попробовать оценить золотое сечение сами, руководствуясь следующими пропорциями:
- Длина отрезка a = 0,618
- Длина отрезка b= 0,382
- Длина отрезка c = 1
- Соотношение c и a = 1,618
- Соотношение c и b = 2,618
Теперь же применим золотое сечение к числам Фибоначчи: берём два соседних члена его последовательности и делим большее на меньшее. Получаем примерно 1,618. Если же возьмём то же самое большее число и поделим его на следующее большее за ним, то получим примерно 0,618. Попробуйте сами: «поиграйте» с числами 21 и 34 или какими-то другими. Если же провести этот опыт с первыми числами последовательности Фибоначчи, то такого результата уже не будет, т.к. золотое сечение «не работает» в начале последовательности. Кстати, чтобы определить все числа Фибоначчи, нужно знать всего лишь три первых последовательных числа.
И в заключение ещё немного пищи для ума.
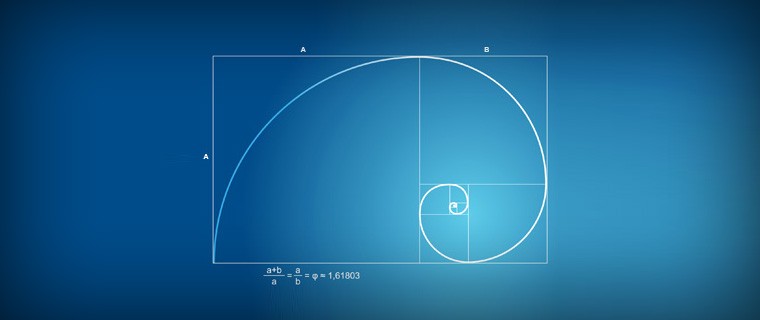
Золотой прямоугольник и спираль Фибоначчи
«Золотой прямоугольник» — это ещё одна взаимосвязь между золотым сечением и числами Фибоначчи, т.к. соотношение его сторон равно 1,618 к 1 (вспоминайте число 1,618!).
Вот пример: берём два числа из последовательности Фибоначчи, например 8 и 13, и чертим прямоугольник с шириной 8 см и длинной 13 см. Далее разбиваем основной прямоугольник на мелкие, но их длина и ширина должна соответствовать числам Фибоначчи – длина одной грани большого прямоугольника должна равняться двум длинам грани меньшего.
После этого соединяем плавной линией углы всех имеющихся у нас прямоугольников и получаем частный случай логарифмической спирали – спираль Фибоначчи. Её основными свойствами являются отсутствие границ и изменение форм. Такую спираль можно часто встретить в природе: самыми яркими примерами являются раковины моллюсков, циклоны на изображениях со спутника и даже ряд галактик. Но более интересно то, что этому же правилу подчиняется и ДНК живых организмов, ведь вы помните, что оно имеет спиралевидную форму?
Эти и многие другие «случайные» совпадения даже сегодня будоражат сознание учёных и наводят на мысль о том, что всё во Вселенной подчинено единому алгоритму, причём, именно математическому. И эта наука кроет в себе огромное количество совсем нескучных тайн и загадок.
Источник
Задача о размножении кроликов
Одним
из наиболее известных математиков эпохи Средневековья по праву
считается Леонардо Пизано Фибоначчи. Позже мы расскажем о Фибоначчи и
его роли в развитии западноевропейской математики более подробно. По
иронии судьбы Фибоначчи, который внес выдающийся вклад в развитие
математики, стал известным в современной математике только лишь как
автор интересной числовой последовательности, называемой числами Фибоначчи. Эта числовая последовательность была получена Фибоначчи при решении знаменитой “задачи о размножении кроликов”.
Формулировка и решение этой задачи считается основным вкладом Фибоначчи
в развитие комбинаторики. Именно с помощью этой задачи Фибоначчи
предвосхитил метод рекуррентных соотношений, который считается
одним из мощных методов решения комбинаторных задач. Рекуррентная
формула, полученная Фибоначчи при решении этой задачи, считается первой в
истории математики рекуррентной формулой.
Существо своей “задачи о размножении кроликов” Фибоначчи сформулировал предельно просто:
“Пусть
в огороженном месте имеется пара кроликов (самка и самец) в первый день
января. Эта пара кроликов производит новую пару кроликов в первый день
февраля и затем в первый день каждого следующего месяца. Каждая
новорожденная пара кроликов становится зрелой уже через месяц и затем
через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько
пар кроликов будет в огороженном месте через год, то есть через 12
месяцев с начала размножения?”
Для решения этой задачи, которая наглядно демонстрируется с помощью рисунка, обозначим через A пару зрелых кроликов, а через B –
пару новорожденных кроликов. Тогда процесс “размножения” может быть
описан с помощью двух “переходов”, которые описывают ежемесячные
превращения кроликов в процессе размножения:
Заметим,
что переход (1) моделирует ежемесячное превращение каждой зрелой пары
кроликов А в две пары, а именно в ту же самую пару зрелых кроликов А и
новорожденную пару кроликов В. Переход (2) моделирует процесс
“созревания” кроликов, когда новорожденная пара кроликов В через месяц
превращается в зрелую пару А. Тогда, если мы начнем в первом месяце со
зрелой пары А, тогда процесс размножения кроликов может быть представлен
с помощью Таблицы 1.
Таблица 1.
| Дата | Пары кроликов | A | B | A + B |
| 1-го января | A | 1 | 1 | |
| 1-го февраля | AB | 1 | 1 | 2 |
| 1-го марта | ABA | 2 | 1 | 3 |
| 1-го апреля | ABAAB | 3 | 2 | 5 |
| 1-го мая | ABAABABA | 5 | 3 | 8 |
| 1-го июня | ABAABABAABAAB | 8 | 5 | 13 |
Заметим, что в столбцах А и В таблицы 1 указаны количества зрелых и новорожденных пар кроликов в каждом месяце года, а в таблице А+В – суммарное количество кроликов.
Изучая последовательности А-, В- и (А+В)-чисел, можно установить следующую закономерность в этих числовых последовательностях: каждый член последовательности равен сумме двух предыдущих. Если теперь обозначить n-й член последовательности, удовлетворяющей этому правилу через Fn, тогда указанное выше общее правило может быть записано в виде следующей математической формулы:
Такая формула называется рекуррентной формулой.
Заметим,
что конкретные значения числовой последовательности, порождаемой
рекуррентной формулой (3), зависят от начальных значений
последовательности F1 и F2. Например, мы имеем F1 = F2 = 1 дляA-чисел и для этого случая рекуррентная формула (3) “генерирует” следующую числовую последовательность:
| 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, … . | (4) |
Для В-чисел мы имеем: F1 = 0 и F2 = 1; тогда соответствующая числовая последовательность для этого случая будет иметь вид:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, … .
Наконец, для (А + В)-последовательности мы имеем: F1 = 1 и F2 = 2; тогда соответствующая числовая последовательность для этого случая будет иметь вид:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, … .
В
математике под числами Фибоначчи, как правило, понимается числовая
последовательность (4). Числа Фибоначчи обладают удивительными
математическими свойствами, но об этом – на следующей странице нашего
Музея.
О кроликах
Думается,
что самое время поговорить о кроликах. Почему именно это животное вошло
в историю математики? Как известно, кролик – это млекопитающее отряда
грызунов семейства зайцев. Первоначальной родиной дикого кролика в
основном считались страны южной части Западной Европы (Испания, Франция,
Италия), откуда кролик был привезен человеком во все страны к северу от
Альпийских гор. Современная область распространения дикого кролика –
вся южная и средняя части Западной Европы, но особенно многочислен он в
странах, прилегающих к Средиземному морю, а также в Африке, Азии,
Австралии, Новой Зеландии, Америке.
Особенностью
кроликов является их удивительная плодовитость. Крольчиха в 3-4 месяца
от роду достигает половой зрелости, причем она способна размножаться
круглый год. Беременность оплодотворенных крольчих длится от 28 до 32
суток (то есть в среднем 30 суток); это означает, что, рассматривая
процесс размножения кроликов, Фибоначчи исходил из реальных фактов
(беременность крольчихи в среднем длится 1 месяц). Но число крольчат,
которые могут быть получены от одной крольчихи в результате одного
окрола, составляет 8-10 (а иногда и больше), то есть на самом деле
кролики размножаются еще более интенсивно, чем предположил Фибоначчи в
своей задаче.
Именно
этой исключительной плодовитостью кроликов объясняется тот факт, что во
многих странах «нашествие кроликов» рассматриваются как национальная
трагедия. Примером является Австралия. Началось все с того, что в
1837 г. один австралийский фермер создал кролеферму из 24 кроликов,
которые, расплодившись и вырвавшись на свободу, уничтожили мало не всю
зелень континента. И только благодаря решительным мерам австралийского
правительства в борьбе с «длинноухой саранчой» удалось сократить
численность прожорливой твари. В Австралии кроликам объявлена настоящая
война, которая уже длится более 150 лет. Через весь материк на многие
сотни километров австралийцы построили «великую китайскую стену» —
барьер, непреодолимый для кроликов; за каждого убитого кролика
выплачивается вознаграждение, против кроликов применяются химические и
биологические средства. Война продолжается с переменным успехом.
Австралийские дикие кролики научились лазить по деревьям, стали ужасно
агрессивными, устраивают уничтожающие набеги на поля и огороды фермеров.
Кроме
того, плодовитое кроличье племя, некогда своеобразно повлиявшее на
выдающегося математика Италии, в настоящее время взяло в осадное
положение итальянский остров Устика (севернее Сицилии). На 1000 жителей
этого крохотного островка приходится 100 000 кроликов. В отличие от
жителей Австралии коренное население Устики сдается без боя: уже пятая
часть жителей эмигрировала с острова.
Но
не следует забывать и о другой стороне «кроличьей проблемы: кроличье
мясо считается одним из наиболее вкусных и полезных. И одним из
крупнейших производителей кроличьего мяса является Италия, родина
Фибоначчи. В этой связи итальянским (да и не только итальянским)
историкам математики необходимо много поработать, чтобы установить, что
же послужило Фибоначчи первопричиной формулировки «задачи о размножении
кроликов»: пристрастность к крольчатине или любовь к высшей математике.
Источник
Институт Золотого Сечения – Под знаком “Золотого Сечения”
Стахов А.П.
Под знаком «Золотого Сечения»:
Исповедь сына студбатовца.
Глава 3. Что такое «золотое сечение»?
3.4. Задача о размножении кроликов
Одним из наиболее известных математиков эпохи Средневековья по праву считается Леонардо Пизано Фибоначчи. Позже я расскажу о Фибоначчи и его роли в развитии западноевропейской математики более подробно. По иронии судьбы Фибоначчи, который внес выдающийся вклад в развитие математики, стал известным в современной математике только лишь как автор интересной числовой последовательности, называемой числами Фибоначчи. Эта числовая последовательность была получена Фибоначчи при решении знаменитой «задачи о размножении кроликов». Формулировка и решение этой задачи считается основным вкладом Фибоначчи в развитие комбинаторики. Именно с помощью этой задачи Фибоначчи предвосхитил метод рекуррентных соотношений, который считается одним из мощных методов решения комбинаторных задач. Рекуррентная формула, полученная Фибоначчи при решении этой задачи, считается первой в истории математики рекуррентной формулой.
Существо своей «задачи о размножении кроликов» Фибоначчи сформулировал предельно просто:
«Пусть в огороженном месте имеется пара кроликов (самка и самец) в первый день января. Эта пара кроликов производит новую пару кроликов в первый день февраля и затем в первый день каждого следующего месяца. Каждая новорожденная пара кроликов становится зрелой уже через месяц и затем через месяц дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в огороженном месте через год, то есть через 12 месяцев с начала размножения?»
Кролики Фибоначчи
Для решения этой задачи, которая наглядно демонстрируется с помощью рисунка, обозначим через A пару зрелых кроликов, а через B – пару новорожденных кроликов. Тогда процесс «размножения» может быть описан с помощью двух «переходов», которые описывают ежемесячные превращения кроликов в процессе размножения:
Заметим, что переход (1) моделирует ежемесячное превращение каждой зрелой пары кроликов А в две пары, а именно в ту же самую пару зрелых кроликов А и новорожденную пару кроликов В. Переход (2) моделирует процесс «созревания» кроликов, когда новорожденная пара кроликов В через месяц превращается в зрелую пару А. Если теперь мы начнем в первом месяце со зрелой пары А, тогда процесс размножения кроликов может быть представлен с помощью Таблицы 1.
Таблица 1
Дата | Пары кроликов | A | B | A+B |
1-го января | A | 1 | 1 | |
1-го февраля | AB | 1 | 1 | 2 |
1-го марта | ABA | 2 | 1 | 3 |
1-го апреля | ABAAB | 3 | 2 | 5 |
1-го мая | ABAABABA | 5 | 3 | 8 |
1-го июня | ABAABABAABAAB | 8 | 5 | 13 |
Заметим, что в столбцах А иВ таблицы 1 указаны количества зрелых и новорожденных пар кроликов в каждом месяце года, а в таблице А+В – суммарное количество кроликов.
Изучая последовательности А-, В- и (А+В)-чисел, можно установить следующую закономерность в этих числовых последовательностях: каждый член последовательности равен сумме двух предыдущих. Если теперь обозначить n-й член последовательности, удовлетворяющей этому правилу через Fn, тогда указанное выше общее правило может быть записано в виде следующей математической формулы:
Такая формула называется рекуррентной формулой.
Заметим, что конкретные значения числовой последовательности, порождаемой рекуррентной формулой (3), зависят от начальных значений последовательности F1 и F2. Например, мы имеем F1= F2=1 для A-чисел и для этого случая рекуррентная формула (3) «генерирует» следующую числовую последовательность:
| 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233,…. | (4) |
Для В-чисел мы имеем: F1=0 и F2=1; тогда соответствующая числовая последовательность для этого случая будет иметь вид:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89,….
Наконец, для (А+В)-последовательности мы имеем: F1=1 и F2=2; тогда соответствующая числовая последовательность для этого случая будет иметь вид:
1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144,….
В математике под числами Фибоначчи, как правило, понимается числовая последовательность (4). Числа Фибоначчи обладают удивительными математическими свойствами и об этом я расскажу ниже.
О кроликах
Думается, что самое время поговорить о кроликах. Почему именно это животное вошло в историю математики? Как известно, кролик – это млекопитающее отряда грызунов семейства зайцев. Первоначальной родиной дикого кролика в основном считались страны южной части Западной Европы (Испания, Франция, Италия), откуда кролик был привезен человеком во все страны к северу от Альпийских гор. Современная область распространения дикого кролика – вся южная и средняя части Западной Европы, но особенно многочислен он в странах, прилегающих к Средиземному морю, а также в Африке, Азии, Австралии, Новой Зеландии, Америке.
Особенностью кроликов является их удивительная плодовитость. Крольчиха в 3-4 месяца от роду достигает половой зрелости, причем она способна размножаться круглый год. Беременность оплодотворенных крольчих длится от 28 до 32 суток (то есть в среднем 30 суток); это означает, что, рассматривая процесс размножения кроликов, Фибоначчи исходил из реальных фактов (беременность крольчихи в среднем длится 1 месяц). Но число крольчат, которые могут быть получены от одной крольчихи в результате одного окрола, составляет 8-10 (а иногда и больше), то есть на самом деле кролики размножаются еще более интенсивно, чем предположил Фибоначчи в своей задаче.
Именно этой исключительной плодовитостью кроликов объясняется тот факт, что во многих странах «нашествие кроликов» рассматриваются как национальная трагедия. Примером является Австралия. Началось все с того, что в 1837 г. один австралийский фермер создал кролеферму из 24 кроликов, которые, расплодившись и вырвавшись на свободу, уничтожили мало не всю зелень континента. И только благодаря решительным мерам австралийского правительства в борьбе с «длинноухой саранчой» удалось сократить численность прожорливой твари. В Австралии кроликам объявлена настоящая война, которая уже длится более 150 лет. Через весь материк на многие сотни километров австралийцы построили «великую китайскую стену» барьер, непреодолимый для кроликов; за каждого убитого кролика выплачивается вознаграждение, против кроликов применяются химические и биологические средства. Война продолжается с переменным успехом. Австралийские дикие кролики научились лазить по деревьям, стали ужасно агрессивными, устраивают уничтожающие набеги на поля и огороды фермеров.
Кроме того, плодовитое кроличье племя, некогда своеобразно повлиявшее на выдающегося математика Италии, в настоящее время взяло в осадное положение итальянский остров Устика (севернее Сицилии). На 1000 жителей этого крохотного островка приходится 100 000 кроликов. В отличие от жителей Австралии коренное население Устики сдается без боя: уже пятая часть жителей эмигрировала с острова.
Но не следует забывать и о другой стороне «кроличьей проблемы: кроличье мясо считается одним из наиболее вкусных и полезных. И одним из крупнейших производителей кроличьего мяса является Италия, родина Фибоначчи. В этой связи итальянским (да и не только итальянским) историкам математики необходимо много поработать, чтобы установить, что же послужило Фибоначчи первопричиной формулировки «задачи о размножении кроликов»: пристрастность к крольчатине или любовь к высшей математике.
(продолжение следует)
Стахов А.П., Под знаком «Золотого Сечения»: Исповедь сына студбатовца. Глава 3. Что такое «золотое сечение»? 3.4. Задача о размножении кроликов // «Академия Тринитаризма», М.,
Эл № 77-6567,
публ.13159, 30.03.2006
[Обсуждение на форуме «Публицистика»]
Источник
