Какие в математике бывают свойства чисел

Ниже приведены характеристики чисел с примерами, которые рассматривает сайт aboutnumber.ru
Сумма цифр
Сумма цифр, из которых состоит число.
62316 → 6 + 2 + 3 + 1 = 18
Произведение цифр
Произведение цифр, из которых состоит число.
872 → 8 * 7 * 2 = 112
Количество цифр в числе
Отображение количества цифр в числе (если их больше 4-х). Это удобно, так как не всегда можно на глаз определить
порядок числа.
57348920572348 → 14
Все делители числа
Полный список делителей, на которые делится число без остатка.
2612 → 1, 2, 4, 653, 1306, 2612
Наибольший делитель из ряда степеней двойки
Ряд степеней двойки — это ряд вида 1, 2, 4, 8, 16, 32, 64, 128, 256 и т.д.
Эти числа являются основными числами в бинарной математике (в двоичной записи), так как ими можно охарактеризовать
объем
информации.
832 → 64
Количество делителей
Суммарное число делителей.
3638143886 → всего 32 делителя
Сумма делителей
Сумма всех делителей числа.
77432243032 → сумма делителей 145185455700
Простое число
Проверка на простое число. Простое число — это число, которое делится без остатка только на единицу и само себя.
Таким образом у простого числа может быть всего два делителя.
677 → 1 * 677
Полупростое число
Проверка на полупростое число. Полупростое число — число, которое можно представить в виде произведения двух простых чисел.
У полупростого числа два делителя — оба простые числа.
898 → 2 * 449
Обратное число
Два числа называются обратными если их произведение равно единице. Таким образом обратным к заданному числу N всегда
будет 1/N.
125 → 0.008
Проверка: 0.008 * 125 = 1
Факторизация
Факторизация числа — представление числа в виде произведения простых чисел.
220683351 → 3 * 7 * 953 * 11027
Двоичный вид
Двоичное, оно же бинарное представление числа. Это запись числа в системе счисления с основанием два.
72412810 → 101100001100101000002
Троичный вид
Троичное представление числа. Это запись числа в системе счисления с основанием три.
990418010 → 2001220112221113
Восьмеричный вид
Восьмеричное представление числа. Это запись числа в системе счисления с основанием восемь.
9788143604410 → 13312140276148
Шестнадцатеричный вид (HEX)
Шестнадцатеричное представление числа. Часто его пишут английскими буквами «HEX». Это запись числа в системе
счисления с основанием шестнадцать.
12444510 → 1E61D16
Перевод из байтов
Конвертация из байтов в килобайты, мегабайты, гигабайты и терабайты.
29141537 (байт) → 27 мегабайтов 810 килобайтов 545 байтов
Цвет
В случаем, если число меньше чем 16777216, то его можно представить в виде цвета. Шестнадцать миллионов цветов,
которые можно
закодировать стандартной цветовой схемой компьютера.
8293836 →
RGB(126, 141, 204) или #7E8DCC
Наибольшая цифра в числе (возможное основание)
Наибольшая цифра, встречающаяся в числе. В скобках указана система счисления, с помощью которой, возможно, записано
это число.
347524172 → 7 (8, восьмеричный вид)
Перевод двоичной/троичной/восьмеричной записи в десятичную
Число, записанное с помощью единиц и нолей — имеет бинарный вид, таким образом его можно перевести в
десятичную систему счисления.
Число, записанное с помощью единиц, нолей и двоек — имеет троичный вид.
Если с помощью цифр до семи (включая) — восьмеричный вид числа.
111010010010112 → 1492310
120201001200213 → 278227610
745312768 → 1590547010
Число Фибоначчи
Проверка на число Фибоначчи. Числа Фибоначчи — это последовательно чисел, в которых каждый последующий элемент равен
сумме двух предыдущих.
Ряд Фибоначчи: 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377 и т.д.
Позиция в ряду Фиббоначчи
Характеризует порядковый номер числа в ряду Фибоначчи.
21 → 8-е число в ряду Фибоначчи
Нумерологическое значение
Нумерологическое значение вычисляется путем последовательного сложения всех цифр числа до тех пор, пока не
не получится цифра от 0 до 9. В нумерологии каждой цифре соответствует свой характер.
8372890 → 8 + 3 + 7 + 2 + 8 + 9 + 0 = 37 → 3 + 7 = 10 → 1 + 0 = 1
мужество, логика, независимость, самостоятельность, индивидуализм, смелость, решительность, изобретательность
Синус числа
Расчет тригонометрической функции синуса числа в радианах.
Sin(18228730686) = -0.20084127807633853
Косинус числа
Расчет тригонометрической функции косинуса числа в радианах.
Cos(792834113) = 0.6573990013186783
Тангенс числа
Расчет тригонометрической функции тангенса числа в радианах. Чтобы получить котангенс числа, надо единицу поделить на
величину тангенса.
Tan(651946045) = 2.5709703278560982
Натуральный логарифм
Это логарифм числа по основанию константы e ≅ 2,718281828459.
Ln(7788338399) = 22.77589337484777
Десятичный логарифм
Это логарифм числа по основания десять.
LOG(1010432) = 6.004507091707365
Квадратный корень
Квадратный корень из введенного числа.
8512326 → 2917.589073190397
Кубический корень
Кубический корень из введенного числа.
5834788 → 180.02867855810877
Квадрат числа
Число, возведенное в квадрат, то есть умноженное само на себя.
31203^2 = 973627209
Перевод из секунд
Конвертация числа секунд в дни, часы, минуты и секунды.
1805506 (секунд) → 2 недели 6 дней 21 час 31 минута 46 секунд
Дата по UNIX-времени
UNIX-время или UNIX-дата — количество секунд, прошедших с полуночи 1 января 1970 года (по UTC).
Таким образом введенное число можно преобразовать в дату.
5265079917115 → Sun, 04 Nov 2136 10:11:57 GMT
Римская запись
Римская запись числа, в том случае, если оно меньше чем максимальное для римской записи 3999.
2014 → MMXIV
Индо-арабское написание
Запись числа с помощью индо-арабских цифр. Они используются в арабских странах Азии и в Египте.
24579540882896 → ٢٤٥٧٩٥٤٠٨٨٢٨٩٦
Азбука морзе
Число, закодированное с помощью азбуки морзе, каждый символ которой представляется в виде последовательсти
коротких (точка) и длинных (тире) сигналов.
7282077 → –… ..— —.. ..— —– –… –…
MD5
Хэш-сумма числа, рассчитанная по алгоритму MD5.
4706204202547 → db2766a5747fd3f8c8c77a1ddd2e24d0
SHA1
Хэш-сумма числа, рассчитанная по алгоритму SHA-1.
345297 → 3855120d2f9d556544bbd24746d0877b79a023df
Base64
Представление числа в системе Base64, то есть в системе счисления с основанием 64.
78868 → SmF2YVNjcmlwdA==
QR-код числа
Двумерный штрих-код-картинка. В ней зашифровано введенное число.
969393779 →
Источник
Натуральные числа
Натуральные числа определение – это целые положительные числа. Натуральные числа используют для счета предметов и многих иных целей. Вот эти числа:
1; 2; 3; 4;…
Это натуральный ряд чисел.
Ноль натуральное число? Нет, ноль не является натуральным числом.
Сколько натуральных чисел существует? Существует бесконечное множество натуральных чисел.
Каково наименьшее натуральное число? Единица — это наименьшее натуральное число.
Каково наибольшее натуральное число? Его невозможно указать, ведь существует бесконечное множество натуральных чисел.
Сумма натуральных чисел есть натуральное число. Итак, сложение натуральных чисел a и b:
a + b = c
с — это всегда натуральное число.
Произведение натуральных чисел есть натуральное число. Итак, произведение натуральных чисел a и b:
a * b = c
с — это всегда натуральное число.
Разность натуральных чисел Не всегда есть натуральное число. Если уменьшаемое больше вычитаемого, то разность натуральных чисел есть натуральное число, иначе — нет.
Частное натуральных чисел Не всегда есть натуральное число. Если для натуральных чисел a и b
a : b = c
где с — натуральное число, то это значит, что a делится на b нацело. В этом примере a — делимое, b — делитель, c — частное.
Делитель натурального числа — это натуральное число, на которое первое число делится нацело.
Каждое натуральное число делится на единицу и на себя.
Простые натуральные числа делятся только на единицу и на себя. Здесь имеется ввиду делятся нацело. Пример, числа 2; 3; 5; 7 делятся только на единицу и на себя. Это простые натуральные числа.
Единицу не считают простым числом.
Числа, которые больше единицы и которые не являются простыми, называют составными. Примеры составных чисел:
4; 6; 8; 9; 10
Единицу не считают составным числом.
Множество натуральных чисел составляют единица, простые числа и составные числа.
Множество натуральных чисел обозначается латинской буквой N.
Свойства сложения и умножения натуральных чисел:
переместительное свойство сложения
a + b = b + a;
сочетательное свойство сложения
(a + b) + c = a + (b + c);
переместительное свойство умножения
ab = ba;
сочетательное свойство умножения
(ab) c = a (bc);
распределительное свойство умножения
a (b + c) = ab + ac;
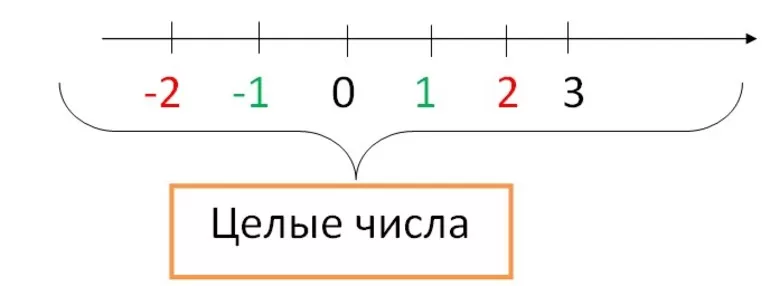
Целые числа
Целые числа — это натуральные числа, ноль и числа, противоположные натуральным.
Числа, противоположные натуральным — это целые отрицательные числа, например:
-1; -2; -3; -4;…
Множество целых чисел обозначается латинской буквой Z.
Рациональные числа
Рациональные числа — это целые числа и дроби.
Любое рациональное число может быть представлено в виде периодической дроби. Примеры:
-1,(0); 3,(6); 0,(0);…
Из примеров видно, что любое целое число есть периодическая дробь с периодом ноль.
Любое рациональное число может быть представлено в виде дроби m/n, где m целое число,n натуральное число. Представим в виде такой дроби число 3,(6) из предыдущего примера:
22/6 = 3,(6);
Другой пример: рациональное число 9 может быть представлено в виде простой дроби как 18/2 или как 36/4.
Ещё пример: рациональное число -9 может быть представлено в виде простой дроби как -18/2 или как -72/8.
Множество рациональных чисел обозначается латинской буквой Q.
Подробнее о рациональных числах в разделе Рациональные числа.
Иррациональные числа
Иррациональные числа — это бесконечные непериодические десятичные дроби. Примеры:
число пи = 3,141592…
число е = 2,718281…
Подробнее об иррациональных числах в разделе Иррациональные числа.
Действительные числа
Действительные числа – это все рациональные и все иррациональные числа.
Множество действительных чисел обозначается латинской буквой R.
Источник
Натуральные числа и их свойства
Для счёта предметов в жизни используют натуральные числа. В записи любого натурального числа используются цифры $0,1,2,3,4,5,6,7,8,9$
Последовательность натуральных чисел, каждое следующее число в котором на $1$ больше предыдущего, образует натуральный ряд, который начинается с единицы (т.к. единица- самое маленькое натуральное число) и не имеет наибольшего значения, т.е. бесконечен.
Нуль не относят к натуральным числам.
Свойства отношения следования
Все свойства натуральных чисел и операций над ними следуют из четырех свойств отношений следования, которые были сформулированы в $1891$ г. Д.Пеано:
Единица- натуральное число, которое не следует ни за каким натуральным числом.
За каждым натуральным числом следует одно и только одно число
Каждое натуральное число, отличное от $1$, следует за одним и только одним натуральным числом
Подмножество натуральных чисел, содержащее число $1$, а вместе с каждым числом и следующее за ним число, содержит все натуральные числа.
Готовые работы на аналогичную тему
Получить выполненную работу или консультацию специалиста по вашему учебному проекту
Узнать стоимость
Если запись натурального числа состоит из одной цифры его называют однозначным (например, $2,6.9$ и т.д.), если запись состоит из двух цифр-двузначным(например,$12,18,45$) и т.д. по аналогии. Двузначные, трехзначные, четырехзначные и т.д. числа называют в математике многозначными.
Свойство сложения натуральных чисел
Переместительное свойство: $a+b=b+a$
Сумма не изменяется при перестановке слагаемых
Сочетательное свойство: $a+ (b+c) =(a+b) +c$
Чтобы прибавить к числу сумму двух чисел, можно сначала прибавить первое слагаемое, а потом, к полученной сумме- второе слагаемое
От прибавления нуля число не измениться и если прибавить к нулю какое- нибудь число, то получится прибавленное число.
Свойства вычитания
Свойство вычитания суммы из числа $a-(b+c) =a-b-c$ если $b+c ≤ a$
Для того, чтобы вычесть сумму из числа, можно сначала вычесть из этого числа первое слагаемое, а затем из полученной разности- второе слагаемое
Свойство вычитания числа из суммы $(a+b) -c=a+(b-c)$, если $c ≤ b$
Чтобы из суммы вычесть число, можно вычесть его из одного слагаемого, а к полученной разности прибавить другое слагаемое
Если из числа вычесть нуль, то число не изменится
Если из числа вычесть его само, то получится нуль
Свойства умножения
Переместительное $acdot b=bcdot a$
Произведение двух чисел не изменяется при перестановке множителей
Сочетательное $acdot (bcdot c)=(acdot b)cdot c$
Чтобы умножить число на произведение двух чисел,можно сначала умножить его на первый множитель, а потом полученное произведение умножить на второй множитель
При умножении на единицу произведение не изменяется $mcdot 1=m$
При умножении на нуль произведение равно нулю
Когда в записи произведения нет скобок, умножение выполняют по порядку слева направо
Свойства умножения относительно сложения и вычитания
Распределительное свойство умножения относительно сложения
$(a+b)cdot c=ac+bc$
Для того чтобы умножить сумму на число,можно умножить на это число каждое слагаемое и сложить получившиеся произведения
Например, $5(x+y)=5x+5y$
Распределительное свойство умножение относительно вычитания
$(a-b)cdot c=ac-bc$
Для того,чтобы умножить разность на число,множно умножить на это число уменьшаемое и вычитаемое и из первого произведения вычесть второе
Например, $5(x-y)=5x-5y$
Сравнение натуральных чисел
Для любых натуральных чисел $a$ и $b$ может выполняться только одно из трех соотношений $a=b$, $a
Меньшим считается число, которое в натуральном ряду появляется раньше, а большим, которое появляется позже. Нуль меньше любого натурального числа.
если $a
Пример 1
Сравнить числа $a$ и $555$, если известно, что существует некоторое число $b$, причем выполняются соотношения: $a
Решение: На основании указанного свойства ,т.к. по условию $a
в любом подмножестве натуральных чисел, содержащем хотя бы одно число, есть наименьшее число
Подмножеством в математике называют часть множества. Говорят, что множество является подмножеством другого, если каждый элемент подмножества является одновременно и элементом большего множества
если $a
Если $c
Часто для сравнения чисел находят их разность и сравнивают ее с нулем. Если разность больше $0$, но первое число больше второго, если разность меньше $0$, то первое число меньше второго.
Округление натуральных чисел
Когда полная точность не нужна, или не возможна ,числа округляют,т.е заменяют их близкими числами с нулями на конце.
Натуральные числа округляют до десятков, сотен,тысяч и т.д
При округлеии числа до десятков его заменяют ближайшим числом,состоящим из целых десятков; у такого числа в разряде единиц стоит цифра $0$
При округлеии числа до сотен его заменяют ближайшим числом,состоящим из целых сотен; у такого числа в разряде десятков и единиц должна стоять цифра $0$. И т.д
Числа,до которых округляют данное называют приближенным значением числа с точностью до указанных разрядов.Например если округлять число $564$ до десятков то получим, что округлить его можно с недостатком и получить $560$, или с избытком и получить $570$.
Правило округления натуральных чисел
Если справа от разряда, до которого округляют число, стоит цифра $5$ или цифра,большая $5$, то к цифре этого разряда прибавляют $1$; в противном случае эту цифру оставляют без изменения
Все цифры, расположенные правее разряда, до которого округляют число ,заменяют нулями
Источник
Исторические данные
Математика зародилась одновременно с необходимостью подсчета. Группа натуральных чисел появилась еще во времена первобытных людей. Они считали количество овец, дней, людей. Позже человек познакомился со сложением и вычитанием. Умножение и деление появились позже, их считали пакетными суммой и разностью (к примеру, 2х3 = 2+2+2).

Ноль первыми начали применять индийские математики. Сначала он использовался как цифра для позиционной записи чисел, постепенно он превратился в полноценную. В Древнем Китае и Индии возникла отрицательная группа, хотя Вавилон, Греция и Египет были не согласны с ее существованим. Если в результате расчетов получалось значение со знаком минус, его отвергали как невозможное. Но Диофант в третьем веке уже умел умножать отрицательные цифры. А через четыре столетия их важность признали и другие математики.
В Европе отрицательные числа считались мнимыми, ложными или абсурдными. И только после выхода работы Пизанского «Книга абака» в 1202 их начали использовать для записи долгов. В XVII веке появилась аналитическая геометрия, цифры со знаком минус нашли свое место на координатной оси. Но еще долгое время оставались непонятными арифметические действия с ними. А в XIX столетии Гамильтон и Грассман создали полную теорию отрицательных чисел.
Свойства чисел
В математике существуют три основных арифметических действия: умножение, сложение и вычитание. И для каждой операции множеству целых чисел присущи некоторые свойства:

- вычитание и сложение — коммутативность, ассоциативность, противоположного элемента и нуля;
- возведение в степень и умножение — добавляется дистрибутивность и свойство единицы;
- упорядоченность;
- делимость.
В первом случае используется правило знаков при открытии скобок: -(-а) = а, -(а+в) = -а-в, -(а-в) = -а+в. Если складываются только положительные или отрицательные значения, то суммируются их величины. А если знаки разные, то из большего вычитают меньшее и приписывают символ уменьшаемого. С целыми выражениями вычитание выполнимо всегда. Некоторым сложно считать выражения с разными знаками. Тогда можно представить себе цифры на координатной оси. При сложении положительных нужно двигаться вправо, отрицательных — влево. В случае вычитания все наоборот.
Произведение чисел с разными знаками отрицательно, в остальных случаях оно положительно: (-а)в = а (-в) = -ав и (-а)(-в) = ав. Целые цифры возводятся в степень так же, как и натуральные. Если это произведение, то нужно возвести каждый множитель, в выражениях с одинаковым основанием показатели складываются, при делении они вычитаются.

Упорядоченность необходима для сравнения целых чисел. Положительными являются те, что больше нуля, отрицательными — меньше. При сравнении выражений с минусовыми знаками большим оказывается то, у которого меньше абсолютная величина.
Делиться целый ряд может с остатком или нацело. В первом случае формула будет содержать делимое, делитель, неполное частное и всегда положительный остаток. Если это деление нацело, то остаток равен нулю. У каждого целого выражения n, которое не равно 0 или 1, есть четыре тривиальных делителя: n и — n, 1 и -1. Если других нет, то это выражение называется простым.
В алгебре для натуральных чисел есть возможность разложить их на простые множители. Это же определение присуще и целой группе, но нужно учитывать знаки.
Основные виды
Есть несколько видов целых выражений, которыми можно оперировать при расчетах. Основные из них:
- вещественные;
- неположительные;
- неотрицательные.
В некоторых задачах ответ нужно округлить до целого значения, то есть заменить его более подходящим выражением из этого ряда. Если оно изменяется в меньшую сторону, то обозначается по правилу Гаусса или Лежандра: [ x ] или E (x). А когда нужно округлить до большего значения, то применяется функция «потолок». Также можно убрать дробную часть или записать ближайшее целое число.

Вещественный ряд в любом случае можно приблизить рациональным, это связывает его с целыми выражениями.
Лучшим инструментом для выполнения этой задачи считаются цепные или непрерывные дроби. К примеру, необходимо разложить число Пи: десятичную дробь 3,14159265 записывают в виде обыкновенных и целого числа — 3, 22/7, 333/106, 355/113. Наиболее подходящим является второе выражение — 22/7.
Целые выражения бывают неположительными и неотрицательными. К первым относят все со знаком минус и нуль, ко вторым — со знаком плюс. А сам 0 нельзя назвать ни положительным, ни отрицательным. Используется такое высказывание для упрощения. Можно не говорить, что а больше или равно нулю, достаточно сказать: оно неотрицательное. Простые примеры целых чисел для двух случаев: 0, 13, 28 и 0, -7, -24.
Описание изменения величин
Класс целых значений применяется для описания изменения различных величин. В частности, с их помощью решают простые задачи: на складе хранится 400 насосов, 300 привезли вчера, а 200 увезли сегодня, нужно найти остаток. Если добавилось 300 предметов, то их записывают со знаком плюс: 400+300 = 700. А для уменьшения количества перед числом ставят минус: 700−200 = 500. Искомое выражение — 500 насосов. Если никаких передвижений товаров не будет, то на неизменность количества укажет нуль.

Основное преимущество целых значений перед натуральными заключается в том, что они четко характеризуют увеличение или уменьшение величин. Удобно использовать их при описании температуры воздуха. Мороз записывают именно отрицательными числами, а тепло — положительными.
А также они применяются в финансовых расчетах. Если человек должен отдать кому-то 10 долларов, то на данный момент у него есть -10 долл. То есть долги можно записать отрицательными числами, а прибыль — положительными. Общую задолженность также узнают с помощью целого ряда: если за электроэнергию нужно заплатить 200 рублей, а за квартплату отдать 100, то вместе счет за коммунальные платежи -200+(-100) = -300 р.
Применение в науках
После того, как стало понятно, что такое целое число в математике, можно разобраться с его применением. А используют этот тип чисел в разных сферах:
- прикладные науки;
- информатика;
- общая алгебра.

При исследованиях различных объектов природы некоторые данные записываются отрицательными и положительными числами. Это удобно в том случае, если приходится составлять таблицы для финансовых отчетов, формировать задачи с неделимыми предметами — временными периодами, единицами техники, живыми объектами.
В физике для описания микромира используются маленькие квантовые числа, все они являются целыми или полуцелыми. А для решения задач с ними разработаны специальные математические методы: теория диофантовых уравнений или целочисленное программирование.
Информатика также оперирует целыми числами. В этой сфере они используются как один из видов данных в языках программирования. Они превращаются в фиксированный набор битов, один из них кодирует знак, а другой сами цифры. У современных компьютеров есть большой набор команд для операций с целочисленными выражениями. В общей алгебре выстроена четкая иерархия множеств. Натуральные числа входят в целые, которые включены в рациональные. Также есть вещественные и иррациональные выражения.
Множества чисел бесконечны. Целых столько же, сколько и натуральных. На них похожи некоторые алгебраические структуры: гауссовы комплексные и формулы Эйзенштейна. С целыми значениями можно выполнять любые арифметические действия, осуществлять проверки и описывать изменения величин.
Источник
