Какие треугольники называются подобными каковы их свойства
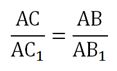
Подобие геометрических фигур
Две фигуры называют подобными, если они переводятся друг в друга путем преобразования подобия (расстояния между точками фигур изменяются одно и то же число раз).
Обозначение подобия фигур: (sim), например (triangle ABCsimtriangle KLM) (треугольник (ABC) подобен треугольнику (KLM))
Признаки подобия треугольников
Для доказательства признаков подобия нам понадобится следующее утверждение:
Лемма
Прямая, параллельная какой-нибудь стороне треугольника и пересекающая две другие стороны, отсекает от него треугольник, подобный исходному.

Источник: wiki.eduvdom.com
Первый признак: подобие по двум углам
Теорема. Если два угла одного треугольника соответственно равны двум углам другого, то такие треугольники подобны.
Докажем данное утверждение.
Дано: (triangle ABC, triangle A_1B_1C_1, angle A=angle A_1, angle B=angle B_1)
Доказать: (triangle ABCsimtriangle A_1B_1C_1)

Источник: wiki.eduvdom.com
Доказательство:
Отложим на (AB) отрезок (BA_2), равный отрезку (A_1B_1) и проведем (A_2C_2parallel AC). Рассмотрим (triangle A_1B_1C_1) и (triangle A_2BC_2: A_1B_1 = A_2B) по построению, (angle B=angle B_1) по условию и (angle A_1=angle A_2) как соответственные при параллельных прямых. Из леммы следует: (triangle A_2BC_2simtriangle ABC), значит,( triangle ABCsimtriangle A_1B_1C_1).
Второй признак: по двум пропорциональным сторонам и углу между ними
Теорема. Если две стороны одного треугольника соответственно пропорциональны двум сторонам другого треугольника и углы между этими сторонами равны, то такие треугольники подобны.
Третий признак: по трем пропорциональным сторонам
Теорема. Если три стороны одного треугольника пропорциональны трём сторонам другого, то такие треугольники подобны.

Источник: sites.google.com
Примеры задач
Задача 1
Через точки (М) и (N) на сторонах (АВ) и (ВС) треугольника (ABC) соответственно, проведена прямая (МN), параллельная стороне (АС), (ВС = 6), (МN = 4) и (АС = 9). Найдите длину (СN).

Источник: egemaximum.ru
Решение:
Рассмотрим (triangle MBN) и (triangle ABC):
- (angle B) — общий
- (angle BMN = angle BAC) как соответственные при (MNparallel AC) и секущей (AB).
Следовательно (triangle MBNsimtriangle ABC)
Можем сделать вывод о пропорциональности соответствующих сторон: (frac{BN}{BC}=frac{MN}{AC}=frac{MB}{AB};)
Пусть (NC = x), тогда (BN = 6 – x). Значит справедливо равенство:
(frac{6-x}6=frac49)
(9(6-x)=6times4)
(x=frac{10}3)
Ответ: (frac{10}3)
Задача 2
Прямая, параллельная основанию треугольника, отсекает от него треугольник и трапецию, площади которых относятся как 4:5 соответственно. Периметр маленького треугольника равен 20 см. Найти периметр данного треугольника.

Источник: egemaximum.ru
Решение:
Имеем соотношение: (frac{S_{DBE}}{S_{ADEC}}=frac45,) значит (frac{S_{DBE}}{S_{ABC}}=frac49) (т.к. всего треугольник условно делится на (4+5=9) частей)
Рассмотрим (triangle DBE) и (triangle ABC):
- (angle B) — общий
- (angle BDE = angle BAC) как соответственные при (DEparallel AC) и секущей (AB)
Следовательно, (triangle DBEsimtriangle AB)C по двум углам.
Площади соотносятся как (k^2) ((k) — коэффициент подобия), значит (k=frac23), то есть (frac{P_{DBE}}{P_{ABC}}=frac23), а так как (P_{DBE}=20), то выражаем (P_{ABC}=30.)
Ответ:30
Насколько полезной была для вас статья?
У этой статьи пока нет оценок.
Выделите текст и нажмите одновременно клавиши «Ctrl» и «Enter»
Текст с ошибкой:
Расскажите, что не так
Источник
План урока:
Пропорциональные отрезки
Определение подобных треугольников
Первый признак подобия треугольников
Второй и третий признаки подобия треугольников
Отношение площадей подобных треугольников
Пропорциональные отрезки
Если известна длина двух отрезков, то можно узнать, во сколько раз один из них больше другого. Например, если некоторый отрезок NM = 24 см, а другой отрезок KP = 4 см, то можно утверждать, что NM в 6 раз длиннее, так как

Величину NM/KP именуют отношением отрезков NM и KP. Надо заметить, что в ряде случаев отношение отрезков можно найти, не зная их длины. Пусть в ∆МКР проведена медиана МН. Очевидно, что отрезок КР будет вдвое длиннее КН, ведь Н – середина КР:

Другой пример – это отношение между диагональю квадрата и его стороной.

Используя теорему Пифагора, несложно показать, что в любом квадрате АВСD

Наконец, в прямоугольном треуг-ке, один из углов которого равен 30°, гипотенуза всегда вдвое длиннее меньшего из катетов:

Если отношение отрезка AB к А1В1 равно отношению отрезка СD к С1D1, то говорят, что отрезки AB и CD пропорциональны отрезкам А1В1 и С1D1. Например, пусть

Получается, AВ и CD пропорциональны А1В1 и С1D1. Важно отметить, что пропорциональны могут быть также сразу три и более отрезка.
Определение подобных треугольников
В жизни нередко можно наблюдать объекты, у которых совпадает форма, но отличаются размеры. В качестве примера можно привести мяч для настольного тенниса и баскетбольный мяч. Оба этих предмета имеют форму шара, на баскетбольный мяч значительно больше. Другой пример – настоящий танк и игрушка, изображающая его. Часто подобны друг другу матрешки, которые вкладываются друг в друга – все они выглядят одинаково, а отличаются только общим размером. Наконец, подобны и знаменитые египетские пирамиды:

Такие объекты в геометрии именуют подобными. Подобны друг другу любые две окружности и любые два квадрата. Но особо важную роль в геометрии играют подобные треугольники. Рассмотрим это понятие подробнее.
Пусть есть два треуг-ка, ∆AВС и ∆А1В1С1, у которых соответственно равны углы:
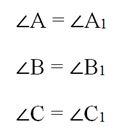
Стороны, которые лежат против одинаковых углов в таких треуг-ках, именуют сходственными. Ими являются стороны AВ и А1В1, ВС и В1С1, АС и А1С1.

Можно дать такое определение подобных треугольников:

Таким образом, подобие треугольников (оно обозначается символом ∾) обозначает выполнение сразу нескольких равенств:

Отношение между сходственными сторонами подобных треуг-ков именуется коэффициентом подобия и обозначается буквой k:

Грубо говоря, подобие треуг-ков означает, что их форма одинакова, но один из них в несколько раз больше или меньше другого. Чтобы получить, из одного треуг-ка другой, равный ему по размерам, его надо просто «масштабировать». Например, на этом рисунке все стороны исходного треуг-ка просто увеличили в три раза:

Это значит, что коэффициент подобия в данном случае равен 3. Однако важно понимать, что в различных геометрических задачах подобные треуг-ки также могут быть повернуты друг относительно друга:

Задание. ∆AВС подобен ∆DEF. Известно, что
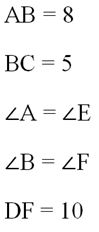
Найдите длину ЕF.

Решение. Как только в задаче появляются подобные треуг-ки, стоит сразу же определить их коэффициент подобия, а для этого надо разобраться, какие стороны будут сходственными. Так как∠А = ∠Е, то лежащие против них стороны DF и ВС– сходственные. Их отношение и будет равно коэффициенту подобия:
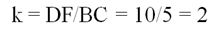
Получили, что стороны ∆DEF вдвое длиннее сходственных им сторон ∆AВС. У подобных треуг-ков углы одинаковы, поэтому∠С = ∠D. Отсюда следует, что стороны AВ и ЕF сходственны, а потому ЕF вдвое больше:
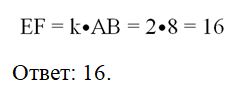
Задание. ∆AВС и∆DEF – подобные. Известно, что
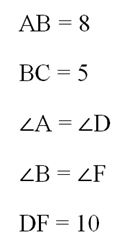
Найдите длину ЕF.

Решение. По сравнению с предыдущей задачей изменилось только одно условие, теперь∠А = ∠D. Однако это меняет сходственные стороны. Из подобия треуг-ков следует, что∠С = ∠Е. Тогда сходственными оказываются уже стороны AВ и DF. Найдем коэффициент подобия треугольников:
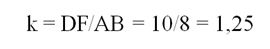
Сходственными являются также стороны ВС и ЕF (ведь∠А = ∠D), поэтому ЕF в 1,25 раза длиннее:
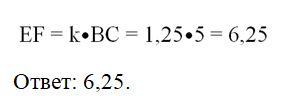
Эти две задачи показывают, как важно правильно определять сходственные стороны подобных треугольников.
Естественно, что все равные друг другу треуг-ки являются одновременно и подобными, причем их коэффициент подобия равен единице.
Задание. Докажите, что у подобных треуг-ков отношение их периметров равно коэффициенту подобия.
Решение. Пусть подобны ∆ AВС и ∆А1В1С1, причем

Периметр ∆AВС можно вычислить так:

Мы доказали утверждение, сформулированное в условии.
Первый признак подобия треугольников
Оказывается, для того, чтобы доказать подобие треуг-ков, не требуется сравнивать все их углы и находить соотношение всех сторон. Существуют три простых признака подобия треугольников.
Однако прежде, чем сформулировать их, нам придется доказать отдельное утверждение, которое известно как обобщенная теорема Фалеса («обычную», не обобщенную теорему мы уже изучали ранее).

Если прямые ВВ1 и СС1 (показаны красным цветом)параллельны, то отрезки AВ и АС пропорциональны отрезкам AВ1 и АС1, то есть справедливо соотношение:
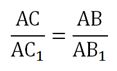
Доказывать будем от противного. Пусть отрезки AВ и АС непропорциональны AВ1 и АС1. Тогда отметим наАС такую точку Н, которая разобьет АС на пропорциональные отрезки, то есть
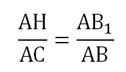
Естественно, эта точка не будет совпадать с С1. Рассмотрим случай, когда она окажется правее, чем С1:

Теперь поступим следующим образом. Проведем через стороны угла большое число прямых, параллельных ВС, которые будут разбивать АС на одинаковые отрезки. По теореме Фалеса эти же прямые отсекут одинаковые отрезки и на AВ. При этом мы проведем настолько много параллельных прямых, что хотя бы одна из них пересечет отрезок С1Н:

Пусть эта прямая пересечет отрезок С1Н в некоторой точке С2, а сторону AВ в точке В2. Ясно, что отрезки AВ и АВ2 пропорциональны отрезкам АС и АС2, так как они состоят из одинакового количества одинаковых отрезков. Например, на построенном рисунке отношение AB2 к AB равно 5/8, так как AB2 состоит из 5 отрезков, отсеченных зелеными параллельными прямыми, а AB состоит из 8 таких отрезков. Аналогично и отношение АС2 к АС также равно 5 к 8. Таким образом, можно записать:

Здесь мы рассмотрели случай, когда точка Н лежит правее С1, то есть АН >C1. Случай, когда АН <АС1, рассматривается аналогично, и также получается противоречие. Эти противоречия означают, что на самом деле точка Н должна совпадать с С1, то есть справедливо равенство
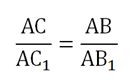
ч.т. д.
Теперь, доказав обобщенную теорему Фалеса, мы можем перейти к первому признаку подобия треугольников.

Действительно, пусть есть ∆AВС и ∆А1В1С1, у которых
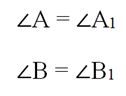
Так как сумма углов у любого треуг-ка постоянна и составляет 180°, то должны быть одинаковы и третьи углы:

При таком наложении прямые ВС и В1С1 окажутся параллельными, так как соответственные углы ∠В1С1А и ∠ВСА одинаковы. Но параллельные прямые должны отсекать на сторонах угла пропорциональные отрезки, то есть

У ∆AВС и ∆А1В1С1 углы одинаковы, а лежащие напротив них стороны пропорциональны, следовательно, это подобные треуг-ки.
Задание. Прямая, параллельная стороне AВ ∆AВС, пересекает стороны ВС и АС в точках Е и Р. Известно, что ЕС = 2, ВЕ = 3, ЕР = 3,2. Какова длина AВ?

Решение. В данной задаче есть только два треуг-ка, ∆AВС и ∆РЕС. Докажем их подобие. У них есть общий∠С, а ∠СЕР = ∠СВА, ведь это односторонние углы при параллельных прямых ЕР и AВ. Отсюда следует, что ∆AВС∾∆РЕС. Значит, ∠А = ∠СРЕ.
Далее надо найти коэффициент подобия. Стороны СЕ и ВС лежат против равных углов∠А и ∠СРЕ, поэтому они сходственные.
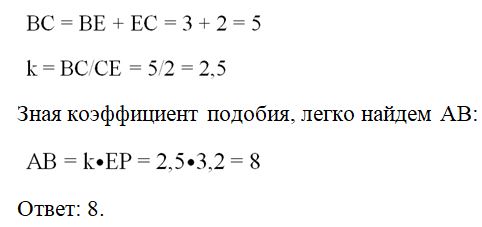
Задание. По данным рисунка найдите длину КЕ:

Решение. На рисунке показано, что ∠ВСА = ∠СКЕ, а∠А = ∠Е = 90°. То есть у ∆AВС и ∆СКЕ есть два одинаковых угла, и, следовательно, они подобны. Сходственными будут являться стороны AВ и ЕС, с их помощью найдем коэффициент подобия:

Задание. Основания трапеции имеют длины 5 и 8 см. Длины ее боковых сторон составляют 3,6 и 3,9 см. Продолжения боковых сторон пересекаются в точке М. Определите расстояние от М до вершин меньшего основания.
Решение. Для начала выполним построение:

Отрезки ВС и АD параллельны, так как они являются основаниями трапеции. Отсюда получаем равенство соответственных углов:
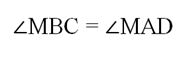
Теперь посмотрим на ∆АМD и ∆ВМС. МЫ только что выяснили, что у них есть одинаковые углы (∠МВС и ∠МАD), а ∠М является общим для них. Тогда получаем, что эти треуг-ки подобны. Стороны ВС и AD будут сходственными, так как лежат против одного и того же ∠М, поэтому по их длине можно найти коэффициент подобия:
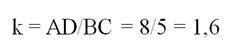
Для нахождения МВ обозначим его длину как х. Тогда отрезок АМ будет иметь длину х + 3,9. Но из подобия треуг-ков следует такое соотношение:
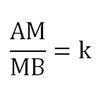
Подставив сюда значение k и выраженные через х длины АМ и МВ, получим уравнение:

МС можно найти таким же путем, обозначив его длину как у. Тогда отрезок МD будет равен у + 3,6, и можно составить уравнение:
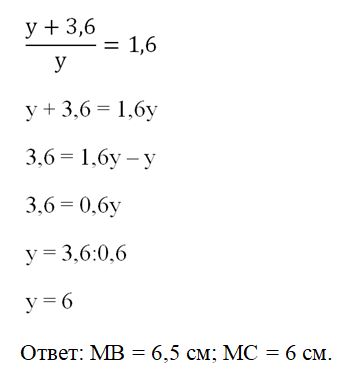
Второй и третий признаки подобия треугольников
Существует ещё два признака подобия треуг-ков, которые в решении задач используются значительно реже. Они выводятся непосредственно из первого признака.

Докажем второй признак подобия. Пусть есть ∆AВС и ∆А1В1С1, для которых выполняются соотношения:
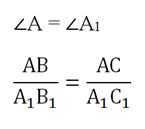
Необходимо доказать, что они подобны. Для этого построим ещё один ∆AВС2, который будет иметь общую сторону с ∆AВС, причем точку С2 мы выберем так, что будут выполняться условия:

∆А1В1С1 и ∆AВС2 будут подобными, ведь у них одинаковы два угла. Значит, будет выполняться соотношение

Но тогда ∆AВС и ∆AВС2 будут равными, ведь у них одинаковы две стороны и угол, образованный этими сторонами:

В итоге у ∆AВС и ∆А1В1С1 оказываются два одинаковых угла, то есть они подобны друг другу
ч. т. д.
Задание. На стороне угла отмечены точки A и В так, что AВ = 5 см и АС = 16 см. На другой стороне этого же угла отмечены точки С и D так, что AD = 8 cм и AF = 10 см. Подобны ли ∆АСD и ∆AFB?
Решение.

У рассматриваемых треуг-ков есть общий угол ∠А. Найдем отношение сторон, прилегающих к этому углу.
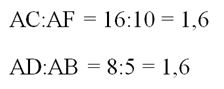
Отношения одинаковы, значит, треуг-ки подобны.
Примечание. В данном случае важно понимать, какие стороны надо делить друг на друга. У ∆АСD известны стороны АС и АD, равные 16 и 8 см. У ∆AFB известны AF и AB, которые составляют 10 и 5 см. Делить надо большую сторону одного треуг-ка на большую сторону другого треуг-ка, то есть 16 на 10. Потом же делим меньшие стороны, то есть 8 на 5.Если получили одно и тоже число, то это значит, что рассмотренные треуг-ки подобны, причем полученное число как раз и является коэффициентом подобия.
Рассмотрим третий признак подобия треуг-ков.

Докажем его. Пусть у ∆AВС и ∆А1В1С1 пропорциональны их стороны:


Можно заметить, что ∆AВС2 и ∆А1В1С1 подобны, ведь у них совпадают два угла. Тогда верны соотношения:

Самая левая дробь в обоих случаях одинакова, а в других отличны лишь числители. Значит, эти числители одинаковы:
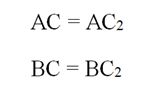
Но тогда у ∆AВС и ∆AВС2 совпадают все стороны, то есть эти треуг-ки равные. Следовательно. Так как ∆AВС2 подобен ∆А1В1С1, то и равный ему ∆AВС также подобен ∆А1В1С1
ч. т. д.
Задание. Подобны ли ∆AВС и ∆DEF, если их стороны имеют длины:

Решение.
Для проверки достаточно просто поделить длины сторон друг на друга. При этом большую сторону одного треуг-ка будем делить на большую сторону другого, а меньшую – на меньшую. Если в результате отношение всех трех сторон будет одинаково, то можно утверждать, что треуг-ки подобны:
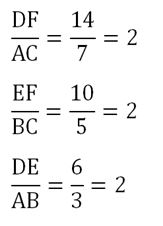
Все три раза мы получали число 2, именно оно и является коэффициентом подобия треуг-ков.
Отношение площадей подобных треугольников
Если треуг-ки подобны, то их стороны отличаются в k раз, где k– коэффициент подобия. А как соотносятся друг с другом длины их высот, медиан и других характерных отрезков. Несложно догадаться, что они также отличаются в k раз.
Докажем это на примере высот. Пусть есть подобные ∆AВС и ∆А1В1С1, причем их коэффициент подобия равен k:
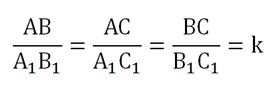
Проведем в них высоты СН и С1Н1:

Теперь сравним ∆АСН и ∆А1С1Н1. Из подобия ∆AВС и ∆А1В1С1 следует, что

Аналогично можно доказать, что в k раз будут отличаться длины медиан и биссектрис.

А каким будет отношение площадей подобных треугольников?Оказывается, что они отличаются уже в k2 раз. Докажем это.
Пусть ∆AВС и ∆А1В1С1 подобны с коэффициентом подобия k. Снова проведем в них высоты СН и СН1:

Запишем очевидные равенства:

В итоге получили, что площади подобных треугольников отличаются в k2 раз.

Задание. Известно, у ∆AВС площадь составляет 10, а отрезок AВ имеет длину 5. ∆DEF подобен ∆AВС, причем сторона DE, сходственная AВ, равна 15. Вычислите площадь ∆DEF.
Решение. По условию задачи легко найти коэффициент подобия ∆AВС и ∆DEF, надо лишь поделить одну сходственную сторону на другую:

Задание. Площади двух подобных треуг-ков составляют 75 м2 и 300 м2. Одна из сторон второго треуг-ка равна 9 м. Вычислите сходственную ей сторону первого треуг-ка.
Решение. Зная площади треуг-ков, легко найдем коэффициент их подобия:
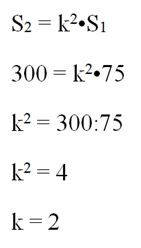
Если коэффициент равен 2, то стороны первого многоугольника вдвое меньше сторон второго, поэтому интересующая нас сторона равна
9:2 = 4,5 м
Ответ: 4,5 м.
Источник
Что такое равные треугольники, понятно более или менее всем: их можно правильно наложить – и они совпадут.
А вот что такое «подобные треугольники»?
Вроде как «похожие», но как это понимать?
Читай эту статью и все поймешь!
Что такое подобные треугольники?
Вот, например, такой и такой:
![]()
Похожи эти треугольники? Ты скажешь, конечно же нет!
А такой и такой?
![]()
Похожи!
А вот такой и такой?
![]()
Посмотри внимательно, тоже похожи.
А теперь строго математически!
Треугольники называются подобными, если у них все углы равны и все стороны пропорциональны.
То есть все углы равны и все стороны одного треугольника в ( displaystyle 5), или, в ( displaystyle 7), или в ( displaystyle 8,21) (или и т.д.) больше сторон другого треугольника.
Записываются слова «треугольник ( displaystyle ABC) подобен треугольнику ( displaystyle {{A}_{1}}{{B}_{1}}{{C}_{1}})» с помощью такого значка:
( displaystyle {} Delta ABCsim{ }Delta {{A}_{1}}{{B}_{1}}{{C}_{1}} )
То число раз, в которое отличаются стороны подобных треугольников, называются коэффициентом подобия, обозначается обычно с помощью буквы ( displaystyle k).
То есть, если
( displaystyle Delta ABCsim{ }Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}) с коэффициентом подобия ( displaystyle k), то это означает что
![]()
(angle A = angle {A_1},angle B = angle {B_1},angle C = angle {C_1})
и ( displaystyle frac{{AB}}{{{A_1}{B_1}}} = k,frac{{AC}}{{{A_1}{C_1}}} = k,frac{{BC}}{{{B_1}{C_1}}} = k)
Можно было бы все так и оставить, но, как и в случае с равенством треугольников, ленивым математикам стало слишком неохота проверять равенство ВСЕХ трех углов, и пропорциональность ВСЕХ трех сторон. И они придумали признаки подобия треугольников.
Признак подобия треугольников «по двум углам»
Если два угла одного треугольника равны двум углам другого треугольника, то такие треугольники подобны.
![]()
( displaystyle left| begin{array}{l}angle A=angle {{A}_{1}}\angle C=angle {{C}_{1}}end{array} right.Rightarrow Delta ABCsim{ }{{A}_{1}}{{B}_{1}}{{C}_{1}})
Помнишь еще, что «( displaystyle sim{ })» обозначает слова «подобен»?
Осознай удобство! Вместо того, чтобы проверять 6 утверждений – 3 равных угла и 3 пропорциональных стороны – ДОСТАТОЧНО РАВЕНСТВА ВСЕГО ДВУХ УГЛОВ! И это вообще-то самых удобный и часто используемый признак.
Но есть и еще два. Смотри.
Признак подобия треугольников «две пропорциональные стороны и угол между ними»
Если треугольники имеют одинаковый угол, и стороны, заключающие этот угол, пропорциональны, то такие треугольники подобны.
![]()
( displaystyle left| begin{array}{l}angle A=angle {{A}_{1}}\frac{AB}{{{A}_{1}}{{B}_{1}}}=frac{AC}{{{A}_{1}}{{C}_{1}}}end{array} right.Rightarrow Delta ABCsim{ }{{A}_{1}}{{B}_{1}}{{C}_{1}})
Признак подобия треугольников «три пропорциональные стороны»
Если три стороны одного треугольника пропорциональны сторонам другого треугольника, то такие треугольники подобны.
![]()
( displaystyle frac{AB}{{{A}_{1}}{{B}_{1}}}=frac{AC}{{{A}_{1}}{{C}_{1}}}=frac{BC}{{{B}_{1}}{{C}_{1}}}Rightarrow Delta ABCsim{ }{{A}_{1}}{{B}_{1}}{{C}_{1}})
Самый главный секрет
Это закрытый контент
Зарегистрируйтесь на YouClever и 100gia и вы получите доступ к нему, а также сможете бесплатно:
- получить доступ к 15 статьям учебника YouClever без ограничений;
- подтянуть слабые места с помощью видеоуроков и записанных вебинаров;
- набить руку, решая задачи и получая проверку и решения;
- проверить свою готовность к ЕГЭ по всем типам задач ЕГЭ (пройдя тест);
- получить персональные скидки на программу “Подготовка к ОГЭ и ЕГЭ на 90+ баллов”
Признаки нам рассказали о том, как обнаружить подобные треугольники, а теперь, как же воспользоваться найденным?
Скажем, ты установил, что ( displaystyle Delta ABCsim{ }Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}) с коэффициентом подобия ( displaystyle 2). Так, кстати, часто бывает, когда проводят среднюю линию…
![]()
Ну вот, что же хорошего? А то, что тогда ВСЕ элементы одного треугольника ровно в ( displaystyle 2) (или сколько у тебя выйдет раз) больше, чем элементы другого треугольника.
НЕ ТОЛЬКО стороны, но и высоты, биссектрисы, медианы, радиусы вписанной и описанной окружности и т.д. Есть одно ВАЖНОЕ исключение: ПЛОЩАДЬ. Запомни:
Отношение площадей подобных треугольников равно КВАДРАТУ коэффициента подобия.
![]()
( displaystyle frac{S}{{{S}_{1}}}={{k}^{2}})
Почему так? А вспомни самую простую формулу площади:
( displaystyle S=frac{1}{2}ah)
Ведь ( displaystyle {{S}_{1}}=frac{1}{2}{{a}_{1}}{{h}_{1}}), и при этом
![]()
( displaystyle frac{a}{{{a}_{1}}}=k), то есть ( displaystyle a={{a}_{1}}cdot k)
( displaystyle frac{h}{{{h}_{1}}}=k), то есть ( displaystyle h={{h}_{1}}cdot k)
Значит, ( displaystyle S=frac{1}{2}k{{a}_{1}}cdot k{{h}_{1}}=frac{1}{2}{{k}^{2}}cdot {{a}_{1}}{{h}_{1}}).
То есть ( displaystyle S={{k}^{2}}cdot {{S}_{1}}) или ( displaystyle frac{S}{{{S}_{1}}}={{k}^{2}}).
КОРОТКО О ГЛАВНОМ
Подобные треугольники – это треугольники, у которых все углы равны и все стороны строго пропорциональны.
Коэффициент пропорциональности называется коэффициентом подобия ( displaystyle k).
Если ( displaystyle Delta ABCsim{ }Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}) с коэффициентом подобия ( displaystyle k), то:
( angle A = angle {A_1},angle B = angle {B_1},angle C = angle {C_1})
( displaystyle frac{{AB}}{{{A_1}{B_1}}} = k,frac{{AC}}{{{A_1}{C_1}}} = k,frac{{BC}}{{{B_1}{C_1}}} = k )
![]()
Отношение периметров подобных треугольников равно коэффициенту подобия: ( displaystyle frac{{{P}_{ABC}}}{{{P}_{{{A}_{1}}{{B}_{1}}{{C}_{1}}}}}=k).
Отношение площадей подобных треугольников равно квадрату коэффициента подобия: ( displaystyle frac{{{S}_{ABC}}}{{{S}_{{{A}_{1}}{{B}_{1}}{{C}_{1}}}}}={{k}^{2}}).
Признаки подобия треугольников:
I признак (по двум углам):
( displaystyle angle A=angle {{A}_{1}}), ( displaystyle angle C=angle {{C}_{1}}) ( displaystyle Rightarrow )( displaystyle Delta ABCsim{ }Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}).
II признак (по одному углу и отношению заключающих его сторон):
( displaystyle angle A=angle {{A}_{1}}), ( displaystyle frac{AB}{{{A}_{1}}{{B}_{1}}}=frac{AC}{{{A}_{1}}{{C}_{1}}}) ( displaystyle Rightarrow )( displaystyle Delta ABCsim{ }Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}).
III признак (по отношению трех сторон):
( displaystyle frac{AB}{{{A}_{1}}{{B}_{1}}}=frac{AC}{{{A}_{1}}{{C}_{1}}}=frac{BC}{{{B}_{1}}{{C}_{1}}}) ( displaystyle Rightarrow )( displaystyle Delta ABCsim{ }Delta {{A}_{1}}{{B}_{1}}{{C}_{1}}).
P.S. Последний бесценный совет ????
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
- проверить свою готовность к каждому типу задач на ЕГЭ (пройдя тест);
- подтянуть слабые места с помощью видеоуроков, вебинаров;
- понять тему с помощью статей учебника YouClever;
- набить руку, решая задачи и получая проверку и решения;
- сдать пробный ЕГЭ и получить сразу оценку и разбор ошибок.
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “
