Какие тела обладают волновыми свойствами
1923 год ознаменовался событием, значимо ускорившим развитие квантовой физики. Французским физиком Л. де Бройлем была предложена гипотеза, предполагающая универсальность корпускулярно-волнового дуализма. В своей концепции Де Бройль сформулировал утверждение о том, что, помимо фотонов и электроны, а также прочие частицы материи имеют как корпускулярные, так и волновые свойства.
Описание гипотезы де Бройля
Идеи де Бройля содержали мысль о том, что любой микрообъект имеет, с одной стороны, корпускулярные характеристики – энергия E и импульс p, а с другой стороны, волновые характеристики – частота v и длина волны λ. При этом количественное соотношение корпускулярных и волновых характеристик аналогично тому же для фотона:
E=hv, p=hvc=hλ.
Как уже было сказано выше, в гипотезе французского физика шла речь о всех видах микрочастиц, соответственно и указанное выше соотношение применимо для любых из них, в том числе, и для обладающих массой m. Любая частица, обладающая импульсом, была сопоставлена с волновым процессом с длиной волны λ=hp.
Для частиц, имеющих массу: λ=hp=h1-v2/c2mv.
В нерелятивистском приближении (υ<<c)
λ=hmv.
Основой идей де Бройля стали размышления о симметрии свойств материи, и в то время, увы, гипотеза не получила опытного подтверждения. Однако, она стала мощнейшим катализатором развития новых идей о природе материальных объектов. На протяжении последующих нескольких лет выдающиеся умы XX века (физики В. Гейзенберг, Э. Шредингер, П. Дирак, Н. Бор и др.) создавали теоретические основы новой науки, названной квантовой механикой.
Дифракция электронов
Впервые гипотеза де Бройля была экспериментально подтверждена в 1927 году, когда американские физики К. Девиссон и Л. Джермер выяснили, что пучок электронов, рассеивающийся на кристалле никеля, дает ясную дифракционную картину, похожую на возникающую тогда, когда на кристалле рассеивается коротковолновое рентгеновское излучение. В исследованиях физиков кристалл служил естественной дифракционной решеткой. По тому, какое положение имели дифракционные максимумы, выяснилась длина волны электронного пучка, и она полностью соответствовала той, что вычислялась по формуле де Бройля.
В 1928 году физик из Англии Г. Томсон (являющийся сыном Дж. Томсона, который открыл за 30 лет до этого электрон) вновь подтвердил гипотезу де Бройля. Эксперименты Томсона позволили наблюдать дифракционную картину, которая возникала, когда пучок электронов проходил через тонкую поликристаллическую фольгу из золота.
Рисунок 5.4.1. Упрощенная схема опытов Г. Томсона по дифракции электронов. K – накаливаемый катод, A– анод, Ф – фольга из золота.
За фольгой установлена фотопластинка, на которой наблюдались явные концентрические светлые и темные кольца. Радиусы этих колец варьировались в зависимости от скорости электронов (т. е. длины волны) согласно де Бройлю (рис. 5.4.2).
Рисунок 5.4.2. Картина дифракции электронов на поликристаллическом образце при длительной экспозиции (a) и при короткой экспозиции (b).
В случае (b) видны точки попадания отдельных электронов на фотопластинку.
В последующие годы эксперимент Г. Томсона многократно повторяли и результат был неизменен даже в тех случаях, когда поток электронов был столь слабым, что через прибор единовременно проходила только одна частица (например, опыт В. А. Фабриканта в 1948 г.). Так была доказана идея, что волновые свойства характерны как для большой совокупности электронов, так и для каждого электрона в отдельности.
В последующем явления дифракции обнаружились и для нейтронов, протонов, атомных и молекулярных пучков. Доказанное экспериментально наличие волновых свойств различных видов микрочастиц позволило сделать вывод об универсальности этого явления в природе, являющегося общим свойством материи. Если продолжать данное рассуждение, волновыми свойствами должны обладать и макроскопические тела. Но из-за больших показателей массы, присущих макроскопическим телам, их волновые свойства затруднительно доказать при помощи экспериментов.
Пример 1
К примеру, пылинка массой 10–9 г, которая движется со скоростью 0,5 м/с, обладает волной де Бройля с длиной примерно 10–21 м, т. е. меньше размера атома на 11 порядков. Подобная длина волны находится за границами области, которая доступна для наблюдения.
Приведенный пример демонстрирует, что для макроскопических тел доступно лишь проявление корпускулярных свойств.
Приведем еще пример.
Пример 2
U = 100 В, длину волны де Бройля для него мы можем определить по формуле: λ=h2meU
Приведенный пример – нерелятивистский случай, поскольку разница между кинетической энергией электрона eU=100 эВ и энергией покоя mc2≈0,5 МэВ достаточно значима (кинетическая энергия значимо меньше энергии покоя).
В результате расчета получим: λ≈0,1 нм, т. е. полученная длина волны примерно соответствует размерам атомов. Для таких электронов кристалл служит отличной решеткой для дифракции. Как раз подобные малоэнергичные электроны показывают четкую дифракционную картину при проведении экспериментов по дифракции электронов. Вместе с этим электрон с такими характеристиками, испытавший дифракционное рассеяние на кристалле как волна, осуществляет взаимодействие с атомами фотопластинки в качестве частицы и вызывает почернение фотоэмульсии в некоторой точке (рис. 5.4.2).
Резюмируя, еще раз отметим, что гипотеза де Бройля о корпускулярно-волновом дуализме, доказанная экспериментально, глобально поменяла представления о том, какими свойствами обладают микрообъекты.
Определение 1
Все микрообъекты обладают и волновыми, и корпускулярными свойствами, но при этом не являются ни волной, ни частицей в стандартном представлении.
Одновременного проявления различных свойств микрообъектов не происходит: они являются дополнением друг друга, и лишь их совокупность характеризует микрообъект в целом.
Эти заключения были сформулированы датским физиком Н.Бором и получили название принципа дополнительности. Упрощенно возможно говорить о том, что микрообъекты распространяются как волны, а обмениваются энергией как частицы.
Если смотреть на вопрос с позиции волновой теории: существует соответствие максимумов в дифракционной картине электронов и максимальной интенсивности волн де Бройля. Наибольшее количество электронов находится в областях максимумов, зарегистрированных на фотопластинке. Однако схема попадания электронов в различные места на фотопластинке не индивидуальна. В принципе нет возможности заранее предположить, куда попадет очередной электрон после рассеяния; допустима только некоторая вероятность попадания электрона в то или иное место. Следовательно, описать состояние микрообъекта и его поведение возможно только, опираясь на понятие вероятности.
Факт, что необходимо использовать вероятностный подход, описывая микрообъекты, является важной отличительной чертой квантовой теории. Квантовая механика для характеристики состояний микрообъектов включает в себя понятие волновой функции Ψ (пси-функции).
Определение 2
Квадрат модуля волновой функции |Ψ|2 пропорционален вероятности нахождения микрочастицы в единичном объеме пространства.
Определенный вид волновой функции задается внешними условиями, в которых находится микрочастица. Математический инструментарий квантовой механики дает возможность определять волновую функцию частицы, которая находится в заданных силовых полях. Безграничная монохроматическая волна де Бройля является волновой функцией свободной частицы, на которую не действуют никакие силовые поля.
Максимально четко явление дифракции наблюдается тогда, когда размерность препятствия, на котором происходит дифракция волн, соизмерима с длиной волны. Подобное поведение характерно для волн любой физической природы и, в частности, электронных волн. Для волн де Бройля естественная дифракционная решетка – это упорядоченная структура кристалла с пространственным периодом порядка размеров атома (приблизительно 0,1 нм). Нет возможности создать искусственным образом препятствие указанного размера (к примеру, отверстие в непрозрачном экране), однако, чтобы уяснить природу волн де Бройля, возможно проводить, так сказать, мысленные эксперименты.
Для примера разберем дифракцию электронов на одиночной щели шириной D (рис. 5.4.3)
Рисунок 5.4.3. Дифракция электронов на щели. График справа – распределение электронов на фотопластинке.
Из общей массы электронов, проходящих через щель, свыше 85% окажутся в центральном дифракционном максимуме. Угловая полуширина θ1 этого максимума определится из условия
Dsinθ=λ
Указанная формула – часть волновой теории. Если рассуждать, опираясь на корпускулярные свойства, возможно сказать, что, когда электрон проходит через щель, он получает дополнительный импульс в перпендикулярном направлении. Можем пренебречь оставшимися 15% электронов, попадающих на фотопластинку за пределами центрального максимума, и тогда будем считать, что максимальное значение py поперечного импульса равно:
pу=p·sin θ1=hλ·sin θ1
В этой формуле p является модулем полного импульса электрона, равным (по гипотезе де Бройля) hλ. Величина p, когда электрон проходит через щель, неизменна, поскольку неизменной является длина волны λ. Указанные выражения дают возможность записать следующее соотношение:
pу=hD
Для задач квантовой механики это несложное с виду соотношение, служащее следствием волновых свойств микрочастицы, имеет глубочайший смысл. Электроны проходят через щель, что есть эксперимент, где y – координата электрона – определяется с точностью Δy = D.
Определение 3
Величина Δy носит название неопределенности измерения координаты.
Вместе с тем, точность определения y – составляющей импульса электрона в момент прохождения через щель – равна py или даже больше, учитывая побочные максимумы дифракционной картины.
Определение 4
Эта величина носит название неопределенности проекции импульса и обозначается как Δpy.
Определение 5
Показатели Δy и Δpy связаны соотношением:
∆у·∆p≥h
и оно названо соотношением неопределенностей Гейзенбурга.
Величины Δy и Δpy следует уяснить в том смысле, что микрочастицы не обладают одновременно точным значением координаты и соответствующей проекцией импульса. Соотношение неопределенностей не имеет отношения к несовершенству используемых приборов, чтобы одновременно измерить координаты и импульс микрочастицы. Соотношение Гейзенбурга есть проявление той самой дуальной корпускулярно-волновой природы материи микрообъектов. Соотношение дает возможность дать оценку тому, насколько применимы к микрочастицам постулаты классической механики. Оно также демонстрирует, что к микрообъектам невозможно применить понятие траектории в классическом понимании, поскольку характеристикой движения по траектории в любой момент времени являются определенные значения координат и скорости. В принципе нет возможности указать траекторию, по которой в некотором мысленном эксперименте двигался некий определенный электрон после прохождения щели до фотопластинки.
И все же определенные условия создают ситуацию, когда соотношение неопределенностей не является противоречием классическому описанию движения тел, в частности, микрочастиц.
Пример 3
К примеру, электронный пучок в кинескопе телевизора при вылете из электронной пушки имеет диаметр D около 10–3 см. В телевизоре ускоряющее напряжение U≈15 кВ.
Нетрудно рассчитать импульс электрона: p=2meU≈6,6·10-23 кг·м/с
Данный импульс имеет направление вдоль оси трубки. Из соотношения неопределенностей вытекает, что электронам при формировании пучка сообщается неконтролируемый импульс Δp, являющийся перпендикуляром к оси пучка: Δp≈hD≈6,6·10–29 кг·м/с.
Допустим, до экрана кинескопа электроны проходят расстояние L≈0,5 м. В таком случае размытие Δlпятна на экране, заданное волновыми свойствами электрона, составит:
∆l≈∆ppL≈5·10-5 см
Так как Δl<<D, возможно рассмотреть движение электронов в кинескопе телевизора при помощи основ классической механики.
Так, используя соотношение неопределенностей, есть возможность выяснять, насколько справедливы законы классической физики в отдельных случаях.
Проведем еще мысленный эксперимент: это будет дифракция электронного пучка на двух щелях
(рис. 5.4.4).
Структура эксперимента аналогична структуре оптического интерференционного опыта Юнга.
Рисунок 5.4.4. Дифракция электронов на двух щелях.
Проанализировав данный эксперимент, мы можем отметить некоторые трудности логических умозаключений в квантовой теории. Собственно, то же затруднение имеет место быть при попытке объяснить оптический опыт Юнга на основе концепции фотонов.
Если в ходе нашего эксперимента закрыть одну из щелей, мы будем наблюдать исчезновение интерференционных полос, а на фотопластинке будет зарегистрировано распределение электронов, продифрагировавших на одной щели (рис. 5.4.3), т.е. долетая до фотопластинки, электроны проходят через одну щель. Открыв обе щели, мы вновь наблюдаем интерференционные полосы, и становится закономерным вопрос: так сквозь какую из щелей проходит каждый электрон?
Конечно, довольно затруднительно представить с точки зрения присущей нашему мышлению логике, что единственным ответом на указанный выше вопрос является факт, что электрон проходит через обе щели. Нашему мышлению свойственно представлять поток микрообъектов в виде направленного движения, например, маленьких шариков и соответственно описывать это движение, опираясь на законы классической физики. Однако для всех микрочастиц характерны как корпускулярные, так и волновые свойства. Нам легко представится, как электромагнитная световая волна пройдёт сквозь две щели в оптическом эксперименте Юнга, поскольку волна не имеет локализации в пространстве. Но при рассмотрении концепции фотонов приходится принять, что и каждый фотон не имеет локализации. Мы не имеем возможности указать, через какую щель прошел фотон, как и не имеем возможности отследить точную траекторию полета фотона до фотопластинки с указанием точной точки его попадания. Опыты демонстрируют такую картину, что, даже когда фотоны проходят сквозь интерферометр поштучно, интерференционная картина после прохождения многих независимых фотонов все равно имеет место быть. Таким образом, квантовая физика формулирует вывод: фотон интерферирует сам с собой.
Сказанное выше имеет отношение и к эксперименту по дифракции электронов на двух щелях. Все известные экспериментальные факты в своей совокупности могут быть объяснены, если признать, что волна по де Бройлю каждого конкретного электрона проходит одномоментно сквозь обе щели, и, как результат, имеет место явление интерференции.
Определение 6
Поштучный поток электронов также дает интерференцию при длительной экспозиции, т. е. электрон, как и фотон, интерферирует сам с собой.
В заключение приведем иллюстрации:
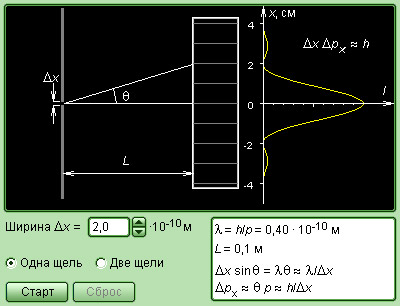
Рисунок 5.4.5. Модель волновых свойств частиц.
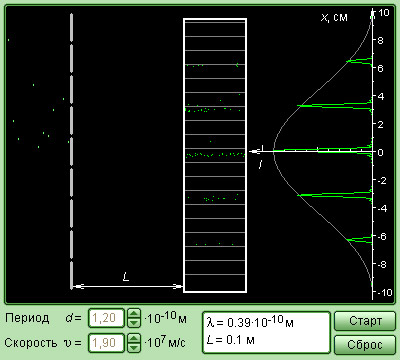
Рисунок 5.4.6. Модель дифракции электронов.
Источник
Главная
Онлайн учебники
База репетиторов России
Тренажеры по физике
Подготовка к ЕГЭ 2017 онлайн
Глава 5. Квантовая физика
Модель 5.3.
Волновые свойства частиц
‘);
magWnd.document.write(‘
Свет обладает как волновыми, так и корпускулярными свойствами. Волновые свойства проявляются при распространении света (интерференция, дифракция). Корпускулярные свойства проявляются при взаимодействии света с веществом (фотоэффект, излучение и поглощение света атомами).
Свойства фотона как частицы (энергия E и импульс p) связаны с его волновыми свойствами (частотой ν и длиной волны λ) соотношениями
E = hν; p = hν / c = h / λ,
где h = 6,63·10–34 Дж·с – постоянная Планка.
Французский физик де Бройль в 1924 г. высказал предположение, что сочетание волновых и корпускулярных свойств присуще не только свету, но и любому материальному телу. Согласно де Бройлю, каждому телу массой m, движущемуся со скоростью υ, соответствует волновой процесс с длиной волны
(нерелятивистское приближение υ << c).
Наиболее отчетливо волновые свойства проявляются у элементарных частиц. Это происходит потому, что из-за малой массы частиц длина волны оказывается сравнимой с расстоянием между атомами в кристаллических решетках. В этом случае при взаимодействии пучка частиц с кристаллической решеткой возникает дифракция.
Для иллюстрации волновых свойств частиц часто используют мысленный эксперимент – прохождение пучка электронов (или других частиц) через щель шириной Δx. С точки зрения волновой теории при дифракции на щели пучок будет уширяться с угловой расходимостью θ ≥ λ / Δx. С корпускулярной точки зрения уширение пучка после прохождения щели объясняется появлением у частиц некоторого поперечного импульса. Разброс значений этого поперечного импульса («неопределенность») есть
Δpx ≈ pθ ≥ (λ / Δx)p = h / Δx.
Соотношение
носит название соотношения неопределенностей. Это соотношение на корпускулярном языке выражает наличие волновых свойств у частиц.
Эксперимент по прохождению пучка электронов через две близко расположенные щели может служить еще более яркой иллюстрацией волновых свойств частиц. Этот эксперимент является аналогом оптического интерференционного опыта Юнга.
Компьютерная модель воссоздает на экране дисплея мысленные эксперименты по дифракции электронов на одной и двух щелях.
Подлетая к экрану со щелями, частицы взаимодействуют с ним как волны де Бройля. Поведение частиц в пространстве между экраном со щелями и фотопластинкой описывается в квантовой физике с помощью Ψ-функций. Квадрат модуля пси-функции определяет вероятность обнаружения частицы в том или ином месте. Таким образом, попадание частиц в различные точки фотопластинки есть вероятностный процесс. Компьютерная модель позволяет продемонстрировать этот процесс.
В случае одиночной щели модель иллюстрирует соотношение неопределенностей, которое является следствием двойственной природы частиц. Можно изменять в некоторых пределах ширину щели и наблюдать дифракционное размытие электронного пучка на фотопластинке.
Предполагается, что электроны имеют энергию порядка 100 эВ.
Обратите внимание, что в случае двух щелей наблюдаемое на фотопластинке распределение не является простым наложением двух независимых распределений от каждой из щелей в отдельности. Появление интерференционных полос на фотопластинке однозначно свидетельствует о том, что каждая достигшая фотопластинки частица одновременно прошла через обе щели экрана.
Источник
Свет обладает как волновыми, так и корпускулярными свойствами. Волновые свойства проявляются при распространении света (интерференция, дифракция). Корпускулярные свойства проявляются при взаимодействии света с веществом (фотоэффект, излучение и поглощение света атомами).
Свойства фотона как частицы (энергия Е и импульс p) связаны с его волновыми свойствами (частотой ν и длиной волны λ) соотношениями
; , (19)
где h=6,63×10-34 Дж – постоянная Планка.
Пытаясь преодолеть трудности боровской модели атома, французский физик Луи де Бройль в 1924 г. выдвинул гипотезу, что сочетание волновых и корпускулярных свойств присуще не только свету, но и любому материальному телу. То есть частицы вещества (например, электроны) обладают волновыми свойствами. высказал предположение, Согласно де Бройлю каждому телу массой m, движущемуся со скоростью υ, соответствует волновой процесс с длиной волны
(20)
. Наиболее ярко волновые свойства проявляются у микрообъектов (элементарных частиц). Вследствие малой массы длина волны де Бройля оказывается сравнимой с межатомным расстоянием в кристаллах. В этих условиях при взаимодействии пучка частиц с кристаллической решеткой возникают дифракционные явления. Электронам с энергией 150 эВ соответствует длина волны λ»10-10 м. Такого же порядка межатомные расстояния в кристаллах. Если пучок таких электронов направить на кристалл, то они будут рассеиваться по законам дифракции. Зафиксированная на фотопленке дифракционная картина (электронограмма) содержит информацию о строении трехмерной кристаллической решетки.
Рисунок 6 Иллюстрация волновых свойств вещества
Для иллюстрации волновых свойств частиц часто используют мысленный эксперимент – прохождение пучка электронов (или других частиц) через щель шириной Δх. С точки зрения волновой теории после дифракции на щели пучок будет уширяться с угловой расходимостью θ»λ/Δх. С корпускулярной точки зрения уширение пучка после прохождения щели объясняется появлением у частиц некоторого поперечного импульса. Разброс значений этого поперечного импульса (“неопределенность”) есть
(21)
Соотношение (22)
носит название соотношения неопределенностей. Это соотношение на корпускулярном языке отражает наличие волновых свойств у частиц.
Эксперимент по прохождению пучка электронов через две близко расположенные щели может служить еще более яркой иллюстрацией волновых свойств частиц. Этот эксперимент является аналогом оптического интерференционного опыта Юнга.
4. 10 Квантовая модель атомаЭкспериментальные факты (дифракция электронов, эффект Комптона, фотоэффект и многие другие) и теоретические модели, вроде боровской модели атома, с определенностью свидетельствуют, что законы классической физики становятся неприменимыми для описания поведения атомов и молекул и их взаимодействия со светом. В течение десятилетия между 1920-м и 1930-м гг. ряд выдающихся физиков ХХ в. (де Бройль, Гейзенберг, Борн, Шредингер, Бор, Паули и др.) занимался построением теории, которая могла бы адекватно описать явления микромира. В результате родилась квантовая механика, ставшая основой всех современных теорий строения вещества, можно сказать, основой (вместе с теорией относительности) физики ХХ в.
Законы квантовой механики применимы в микромире, в то же время мы с вами являемся макроскопическими объектами и живем в макромире, управляющимся совершенно иными, классическими законами. Поэтому неудивительно, что многие положения квантовой механики не могут быть проверены нами непосредственно и воспринимаются как странные, невозможные, непривычные. Тем не менее, квантовая механика является, наверное, самой подтвержденной на опыте теорией, так как следствия расчетов, выполненных по законам этой теории, используются практически во всем, что нас окружает, и стали частью человеческой цивилизации (достаточно упомянуть о тех полупроводниковых элементах, работа которых в данный момент позволяют читателю видеть текст на экране монитора, покрытие которого, кстати, также рассчитано с помощью квантовой механики).
К сожалению, используемый квантовой механикой математический аппарат довольно сложен и идеи квантовой механики могут быть изложены лишь словесно и поэтому недостаточно убедительно. С учетом этого замечания попытаемся дать хоть какое-то представление об этих идеях.
Основным понятием квантовой механики является понятие квантового состояния какого-то микрообъекта, или микросистемы (это может быть отдельная частица, атом, молекула, совокупность атомов и т.п.).
Квантовая модель атома отличается от планетарной в первую очередь тем, что в ней электрон не имеет точно определенной координаты и скорости, поэтому бессмысленно говорить о траектории его движения. Можно определить (и нарисовать) только границы области его преимущественного движения (орбитали).
Состояние какого-то микрообъекта, или микросистемы (это может быть отдельная частица, атом, молекула, совокупность атомов и т.п.) может быть охарактеризовано заданием квантовых чисел: значений энергии, импульса, момента импульса, проекции этого момента импульса на какую-то ось, заряда и т.п.
УРАВНЕНИЕ ШРЕДИНГЕРА для движения электрона в кулоновском поле ядра атома водорода используется для анализа квантовой модели атома. В результате решения этого уравнения получается волновая функция, которая зависит не только от координаты и времени t, но и от 4-х параметров, имеющих дискретный набор значений и называемых квантовыми числами. Они имеют названия: главное, азимутальное, магнитное и магнитное спиновое.
Главное квантовое число n может принимать целочисленные значения 1, 2, … . Оно определяет величину энергии электрона в атоме
(23)
, где Еi – энергия ионизации атома водорода (13,6 эВ).
АЗИМУТАЛЬНОЕ (ОРБИТАЛЬНОЕ) квантовое число l определяет модуль момента импульса электрона при его орбитальном движении (24)
. Оно принимает целочисленные значения l = 0, 1, 2, … n-1 .
МАГНИТНОЕ квантовое число ml определяет проекцию вектора момента импульса орбитального движения электрона LZ на направление внешнего магнитного поля . Оно принимает положительные и отрицательные целочисленные значения, по модулю меньшие или равные l . , (25)
где ml = 0, ±1, ±2, … , ±l .
МАГНИТНОЕ спиновое квантовое число mS определяет проекцию вектора собственного момента импульса электрона (СПИНА ) на направление внешнего магнитного поля :
SZ = mS и принимает только 2 значения: mS = +1/2, -1/2. Для модуля спина , (26)
где s – спиновое квантовое число, которое у каждой частицы имеет только одно значение. Например, для электрона s = (аналогично, для протона и нейтрона). Для фотона s = 1.
Вырожденными называются состояния электрона с одинаковой энергией.
КРАТНОСТЬ ВЫРОЖДЕНИЯравна количеству состояний с одной и той же энергией.
КРАТКАЯ запись состояния электрона в атоме: ЦИФРА, равная главному квантовому числу, и буква, определяющая азимутальное квантовое число:
Таблица 1 Краткая запись состояния электрона в атоме
| Буква | s | p | d | e | f |
| Значение l |
Таблица 2 Краткая запись состояния электрона в атоме
| Серия | Лаймана | Бальмера | Пашена | Брэкета |
| Переходы | np®1s | ns®2p, nd®2p | nf®3d, np®3d | ng®4f, nd®4f |
ПРАВИЛО ОТБОРА азимутального квантового числа Dl = ±1. Электрон в атоме может переходить только между состояниями, удовлетворяющему указанному правилу.
5 Порядок выполнения работы
Источник
