Какие свойство имеют фигуры
В статье описываются геометрические фигуры: определение, основные свойства и формулы.
Плоские геометрические фигуры:
Четырехугольник (общее для всех четырехугольников)
Квадрат
Прямоугольник
Параллелограмм
Ромб
Трапеция
Треугольник
Окружность
Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.
Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.
Четырёхугольник
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.
Основные свойства:
- Сумма углов четырёхугольника равна 360°
- Не существует четырёхугольников, у которых все углы острые или все углы тупые.
- Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
- Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.
В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
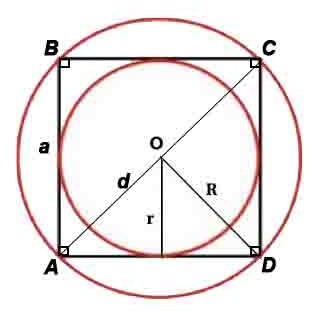
Квадрат
Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Основные формулы:
Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a2или S=d2/2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2
где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.
Свойства:
- Все стороны равны, все углы равны и составляют 90°;
- Диагонали квадрата равны и перпендикулярны;
- У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
- Квадрат является одновременно частным случаем ромба и прямоугольника.
Прямоугольник
Прямоугольник — четырехугольник, у которого все углы прямые.
Основные формулы:
Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a2+b2)/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a2+b2)/2 (теорема Пифагора)
где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a2+b2) – корень квадратный из (a2+b2).
Свойства:
- Диагонали прямоугольника равны и делятся точкой пересечения пополам.
- Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.
Параллелограмм
Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Определения:
Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.
Основные формулы:
Стороны и диагональ связаны соотношением: (d1)2+(d2)2=(a2+b2)*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними: S=(d1*d2)/2*sin γ
где a, b — длины сторон, d1, d2 –диагонали, P-периметр, S-площадь,
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).
Свойства:
- У параллелограмма противоположные стороны равны и противоположные углы равны.
- Сумма любых двух соседних углов параллелограмма равна 180°.
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
- Каждая диагональ делит параллелограмм на два равных треугольника.
- Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
- Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Основные формулы:
Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d1*d2)/2
Радиус окружности, вписанной в ромб: r=h/2 или r =(d1*d2)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a2 · sin α
где a — длина стороны, d1, d2 –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба
Свойства:
- Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
- В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d1*d2/4a.
Трапеция
Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.
Определения:
- Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
- Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
- Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
- Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
- Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
- Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.
Основные формулы:
Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2
где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d1, d2 –диагонали,
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне
Свойства:
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.
Треугольник
Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
Определения:
- Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
- Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
- Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
- Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
- Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
- Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
- Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
- Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
Основные формулы:
Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ
по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c2=a2+b2 (Теорема Пифагора)
где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
d1, d2 –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности
Свойства:
- В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
- Сумма углов треугольника равна 180°:
- Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| <c<a+b
- Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
- Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
- Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
- В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
- Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2=a2+b2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.
Окружность
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.
Определения:
- Радиус — отрезок, который соединяет центр окружности с любой её точкой.
- Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
- Диаметр — хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
- Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
- Секущая — прямая, которая пересекает окружность в двух различных точках.
Основные формулы:
Длина окружности: L = 2πR
Площадь круга: S = π*r2 или S = π*d2/4
где π = 3,14 (3,1415926535) – величина постоянная,
где r-радиус, d –диаметр, L – длина окружности, S-площадь.
Источник
Основные понятия
Основные геометрические фигуры на плоскости состоят из точек, линий, лучей, отрезков и вершин. У каждого предмета есть свои особенности, свойства и предназначение.
Самый минимальный объект в геометрии — точка. Ее особенность в том, что она не имеет измерительных мер: у нее нет высоты, длины, радиуса. У точки можно определить только ее расположение, которое принято обозначать одной заглавной буквой латинского алфавита.
Из множества точек может получится линия, а из нескольких соединенных между собой линий — геометрические фигуры.
Каждая математическая фигура имеет собственную величину, которую можно измерить при помощи формул и внимательности.
Площадь — это одна из характеристик замкнутой геометрической фигуры, которая дает нам информацию о ее размере. S (square) — знак площади.
Периметром принято называть длину всех сторон многоугольника. Периметр обозначается заглавной латинской P.
Если параметры переданы в разных единицах длины, мы не сможем узнать какая площадь фигуры получится. Чтобы правильно решить задачу, нужно перевести все данные к одной единице измерения.
Популярные единицы измерения
- квадратный миллиметр (мм2);
- квадратный сантиметр (см2);
- квадратный дециметр (дм2);
- квадратный метр (м2);
- квадратный километр (км2);
- гектар (га).
Геометрические тела — часть пространства, которая ограничена замкнутой поверхностью своей наружной границы.
Если все точки фигуры принадлежат одной плоскости, значит она является плоской.
Объемная фигура — геометрическая фигура, у которой все точки не находятся на одной плоскости.
Объемные геометрические фигуры:
- шар;
- конус;
- параллелепипед;
- цилиндр;
- пирамида;
- сфера.
В начальной школе дети узнают названия геометрических фигур и учатся различать плоские от объемных. Сейчас мы рассмотрим подробнее некоторые фигуры, разберем их определения и свойства.
На уроках математики в Skysmart дети решают увлекательные задачки в интерактивном формате, рисуют пальцами на онлайн-доске и помогают героям красочных комиксов. Приходите вместе с ребенком на бесплатный вводный урок: познакомимся, покажем, как все устроено на платформе и наметим вдохновляющую программу обучения.
Прямоугольник
Прямоугольник — четырехугольник, у которого все стороны пересекаются под прямым углом.
Свойства прямоугольника:
- Диагонали прямоугольника равны и делятся в точке пересечения пополам.
- Около прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.
Узнать площадь прямоугольника помогут следующие формулы:
- S = a * b, где a, b — ширина и высота прямоугольника.
- S = a * √(d2 – а2), где а — известная сторона, d — диагональ.
Диагональ — это отрезок, который соединяет противоположные стороны фигуры. Он есть во всех фигурах, число вершин которых больше трех.
- S = 0,5 ∗ d2 ∗ ????????????(????), где d — диагональ.
Периметр прямоугольника — сумма длины и ширины, умноженная на два.
P = 2 * (a + b), где a — ширина, b — высота.
Квадрат
Квадрат — это тот же прямоугольник, у которого все стороны равны.
Свойства квадрата:
- Все стороны и углы равны и составляют 90 градусов.
- Диагонали квадрата равны и перпендикулярны.
- У квадрата центры вписанной и описанной окружности совпадают и находятся в точке пересечения его диагоналей.
Найти площадь квадрата легко:
- S = а2, где a — сторона квадрата.
- S = d2 : 2, где d — диагональ.
Периметр квадрата — это произведение длины стороны на четыре.
P = 4 * a, где a — длина стороны.
Трапеция
Трапеция — это четырёхугольник, у которого две стороны параллельны, а две не параллельны.
Основное свойство: в трапецию можно вписать окружность, если сумма ее основ равна сумме боковых сторон.
Как найти площадь трапеции:
S = (a + b) : 2 * h, где a, b — два разных основания, h — высота трапеции.
Построить высоту трапеции можно, начертив отрезок так, чтобы он соединил параллельные стороны и пересек их под прямым углом.
Формула периметра для равнобедренной трапеции отличается от прямоугольника тем, что у первого есть две равные стороны.
P = a + b + 2 * c, где a, b — параллельные стороны, c — две длины одинаковых сторон.
Параллелограмм и ромб
Параллелограмм — четырехугольник, противоположные стороны которого попарно параллельны. Определение ромба звучит точно также, поэтому мы их объединили.
Свойства фигур:
- Противоположные стороны и углы равны.
- Сумма любых двух соседних углов равна 180 градусов.
- Диагонали пересекаются и точкой пересечения делятся пополам.
- Каждая диагональ делит фигуру на два равных треугольника.
Общие формулы расчета площади фигур:
- S = a * h, где a — сторона, h — высота.
- S = a * b * sinα, где a и b — две стороны, sinα — синус угла между ними.
- S = 0,5 * (d1 * d2), где d1,d2 — две диагонали.
Периметр ромба — это произведение длины стороны на четыре.
P = 4 * a, где a — длина стороны.
Периметр параллелограмма — сумма длины и ширины, умноженная на два.
P = 2 * (a + b), где a — ширина, b — высота.
Треугольник
Треугольник — это когда три отрезка соединяют три точки, не лежащие на одной прямой. Эти три точки принято называть вершинами, а отрезки — сторонами.
Виды треугольника:
- Прямой. Один угол прямой, два других менее 90 градусов.
- Острый. Градус угла больше 0, но меньше 90 градусов.
- Тупой. Один угол тупой, два других острые.
Свойства треугольника:
- В треугольнике против большего угла лежит большая сторона — и наоборот.
- Сумма углов треугольника равна 180 градусов.
- Все углы равностороннего треугольника равны 60 градусам.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов.
Рассчитать площадь треугольника можно несколькими способами по исходным данным, давайте их рассмотрим.
- Если известна сторона и высота.
S = 0,5 * a * h, где a — длина основания, h — высота, проведенная к основанию.
Основание может быть расположено иначе, например так:
При тупом угле высоту можно отразить на продолжение основания:
При прямом угле основанием и высотой будут его катеты:
- Если известны две стороны и синус угла.
S = 0,5 * a * b * sinα, где a и b — две стороны, sinα — синус угла между ними.
- Если есть радиус описанной окружности.
S = (a * b * с) : 4 * R, где a, b и с — стороны треугольника, а R — радиус описанной окружности.
- Если есть радиус вписанной окружности.
S = p * r, где р — полупериметр треугольника, r — радиус вписанной окружности.
Периметр треугольника — это сумма длин трех его сторон.
P = a + b + c, где a, b, c — длина стороны.
Формула измерения периметра для равностороннего треугольника — это произведение длины стороны на три.
P = 3 * a, где a — длина стороны.
Подружиться с геометрией помогут внимательные учителя-профессионалы Skysmart. Они найдут подход к любому ребенку: объяснят сложную тему, ответят на неловкие вопросы и вдохновят на учебу. А если что-то пойдет не так — учителя можно поменять.
Записывайтесь на бесплатный урок математики и начните заниматься в удовольствие и в комфортном темпе.
Круг
Круг — это когда множество точек на плоскости удалены от центра на равном радиусу расстоянии.
Окружность — это граница круга.
Радиус круга — это расстояние от центра окружности до любой ее точки.
Диаметр круга — это отрезок, который соединяет две точки окружности и проходит через её центр. Диаметр круга равен двум его радиусам.
Формулы площади круга:
- S = π * r2, где r — это радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
- S = d2 : 4 * π, где d — это диаметр.
- S = L2 : 4 * π, где L — это длина окружности.
Периметр круга или длина окружности — это произведение радиуса на два Пи или произведение диаметра на Пи.
L = d * π = 2 * r * π, где d — диаметр, r — радиус, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна 3,14.
Источник
Александр А.
18 мая 2019 · 8,0 K
Копирайтер, увлекаюсь психологией и философией. Люблю искусство и моду
Фигуры на плоскости изучают раздел геометрии- планиметрия. Геометрическая фигура-это любое множество точек.
Если все точки геометрической фигуры принадлежат одной плоскости, она называется плоской. Например, отрезок, прямоугольник – это плоские фигуры. Существуют фигуры, не являющиеся плоскими. Это, например, куб, шар, пирамида.
Основные свойства простых фигур выражаются в аксиомах:
- Какова бы ни была прямая, существуют точки, принадлежащие этой прямой и не принадлежащие ей.
Через любые две точки можно провести прямую, и только одну.
Эта аксиома выражает основное свойство принадлежности точек и прямых на плоскости.
- Из трех точек на прямой одна и только одна лежит между двумя другими.
Этой аксиомой выражается основное свойство расположения точек на прямой.
- Каждый отрезок имеет определенную длину, большую нуля. Длина отрезка равна сумме длин частей, на которые он разбивается любой его точкой.
Очевидно, что аксиома 3 выражает основное свойство измерения отрезков.
- Прямая разбивает плоскость на две полуплоскости.
Этим предложением выражается основное свойство расположения точек относительно прямой на плоскости.
Какой фигурой является спираль: плоской или объёмной?
Спираль – вообще обычно в математике это именно кривые в плоскости.
В обиходе их часто путают с винтовыми линиями – пространственными кривыми (вроде резьбы на винте).
Но в то же время сами математики иногда называют винтовые линии трехмерными спиралями. Так что термин не очень строгий
Как различаются типы кристаллической решетки? Какие способы определения?
Человек науки, полиглот, энтузиаст. Химия, компьютерные технологии, нейропсихоло…
Существует 4 типа кристаллических решеток: ионные, молекулярные, атомные и металлические.
В узлах ионных кристаллических решеток находятся ионы, как можно понять из названия. Такой тип решетки характерен для солей, оксидов и некоторых гидроксидов. Например, самый яркий представитель – NaCl. Вещества подобного строения характеризуются высокой твердостью, тугоплавкостью и нелетучестью.
В молекулярных кристаллических решетках в узлах находятся молекулы. Такие решетки могут быть полярные и неполярные. Например, I2 или N2 – неполярные, а HCl или H2O – полярные. Характерны для жидких и газообразных веществ (при н.у.). Так как молекулярные взаимодействия слабые, то и кристаллические решетки эти будут нетвердые, летучие и с низкой температурой плавления. К таким решеткам относят твердую органику (сахар, глюкоза, нафталин).
В атомных кристаллических решетках в узлах находятся атомы, связанные друг с другом прочными ковалентными связями. Такая решетка характерна простым веществам неметаллам, которые при нормальных условиях находятся в твердом состоянии, например алмаз. Температура плавления у подобных веществ очень высокая, они прочные, твердые и нерастворимы в воде.
Металлические решетки характеризуются тем, что в узлах находятся атомы или ионы одного или нескольких металлов (у сплавов). Для металлических решеток характерно наличие так называемого общего электронного облака. Так как непрерывно происходит процесс перехода валентных электронов одного атома к другому с образованием иона, то можно говорить о том, что электроны свободно двигаются в объеме всего металла. Этим свойством объясняется электро- и теплопроводность металлов. Вещества такого строения ковки и пластичны.
Вообще в материаловедении для изучения кристаллических структур существует множество методов, основанных на свойствах рентгеновского излучения (дифракция, интерференция), электронографический анализ и другие. Но если вы хотите просто определить тип решетки вещества известного состава, нужно понять к какому классу веществ оно относится и какие физико-химические свойства имеет.
Прочитать ещё 1 ответ
смысл симметрии?
Пользователь данного сайта
Смысл это либо цель, либо значение.
Цель симметрии – вопрос неконкретный, нужно понимать, кто создал и создвал ли кто-то специально симметрию, чтоб было понятно, есть ли цель. Значение симметрии – это зеркальное повторение частей предмета или вращательное повторение частей предмета. Например, цветок с 5 одинаковыми лепестками может иметь симметрию вращения.
Помимо цели и значения, у наблюдателя явления симметрии есть восприятие. Оно накладывает свои оценки – красиво или некрасиво, ожидаемо или неожиданно.
Прочитать ещё 1 ответ
Источник
