Какие свойства выполняются для длин отрезков
Лекция 10. Длина отрезка и её измерение.
Понятие длины отрезка и ее измерения используется во многих областях деятельности человека и научных исследованиях. Поэтому рассмотрим эту величину более детально.
Определение. Длиной отрезка называется положительная величина, определенная для каждого отрезка, так, что: 1) равные отрезки имеют равные длины; 2) если отрезок состоит из конечного числа отрезков, то его длина равна сумме длин этих отрезков.
Процесс измерения длины отрезков выглядит так. Из множества отрезков выбирают какой-нибудь отрезок е и принимают его за единицу длины. На отрезке а, длину которого измеряют, от одного из его концов откладывают последовательно отрезки, равные е, до тек пор, пока это возможно. Если отрезки, равные е, отложились n раз и конец последнего отрезка совпал с концом отрезка а, то говорят, что значение длины отрезка а есть натуральное число n и пишут а = n е. Если же отрезки, равные е, отложились n раз, и еще остался остаток, меньший е, то на нем откладывают отрезки, равные е1 = 110 е. Если они отложились ровно n1раз, то тогда а = n, n1 е, и значение длины отрезка есть конечная десятичная дробь. Если же отрезок е1 отложился n1 раз и остался еще остаток, меньший е1, то на нем откладывают отрезки, равные е2= 1100е1. Если представить этот процесс бесконечно продолженным, то получим, что значение длины отрезка а есть бесконечная десятичная дробь. Таким образом, при выбранной единице длины длина любого отрезка выражается положительным действующим числом. Вполне очевидно, что верно и обратное: если дано положительное действительное число, то всегда можно построить отрезок, численное значение которого выражается этим действительным числом.
Нетрудно доказать следующие свойства длин отрезков.
1. При выбранной единице длины длина любого отрезка выражается положительным действительным числом и для каждого положительного действительного числа есть отрезок, длина которого выражается этим числом.
2. Если два отрезка равны, то и численные значения их длин также равны, и обратно: если численные значения длин отрезков равны, то и равны сами отрезки, т.е. а = в mе (а) = mе (в).
3. Если данный отрезок равен сумме нескольких отрезков, то численное значение его длины равно сумме численных значений длин отрезков слагаемых и, обратно, если численное значение длины отрезка равно сумме численных значений отрезков слагаемых, то и сам отрезок равен сумме этих отрезков, т.е. с = а + в mе (с) = mе (а) + mе (в).
4. Если длины отрезков а и в таковы, что в = х ∙ а, где х – положительное действительное число и длина отрезка а измерена при помощи единицы измерения е, то, чтобы найти численное значение отрезка в при единице измерения е, достаточно число х умножить на численное значение длины отрезка а при единице измерения е, т.е. в = х а mе (в) = х mе (а).
5. При замене единицы измерения длины численное значение длины отрезка увеличивается (уменьшается) во столько раз, во сколько новая единица измерения длины отрезка меньше (больше) старой. Из других свойств длины отрезков отметим следующие.
6.а > в mе (а) >mе (в);
7.с = а – в mе (с) = mе (а) – mе (в);
8.х = а : в х = mе (а) : mе (в).
Все эти свойства позволяют сравнение длин отрезков и действия над ними сводить к сравнению и действием над соответствующими числовыми значениями длин этих отрезков. На практике, сравнивая длины отрезков и выполняя действия над длинами отрезков, теоретические положения, сформулированные выше, используются неявно.
Примеры.
1. 12 м < 12,3 м, так как 12 < 12,3.
2. 8,8 см + 3,4 см = (8,8 + 3,4) см = 12,2 см.
3. 18 ∙ 3 дм = (18 ∙ 3) дм = 54 дм.
Приводим несколько типичных задач.
Задача 1. Постройте отрезок, длина которого 3,2Е. Каким будет численное значение длины этого отрезка, если единицу длины Е увеличить в 3 раза?
Решение. Построим произвольный отрезок и будем считать его единичным. Затем построим прямую, отметим на ней точку А и отложим от нее 3 отрезка, длины которых равны Е. Получим отрезок АВ, длина которого 3Е. Чтобы получить отрезок длиной 3,2Е, надо ввести новую единицу длины. Для этого единичный отрезок надо разбить либо на 20 равных частей, либо на 5, поскольку 0,2 = 15. Если от точки В отложить отрезок, равный 15 единичного, то длина отрезка АС будет равна 3,2Е.
Чтобы выполнить второе требование задачи, воспользуемся свойством 3, согласно которому при увеличении единицы длины в 3 раза численное значение длины данного отрезка уменьшается в 3 раза. Разделим 3,2 на 3, получим: 3,2 : 3 = 3 15 : 3 = 1615 = 1115.
Таким образом, при единице длины 3Е численное значение длины построенного отрезка АС будет равно 1115.
Задача 2. Начертите два отрезка: длина первого – 8 см, а другой – в 2 раза длиннее. Чему равна длина второго отрезка?
Решение. 1 способ. Строят отрезок 6 см, а затем на луче ОА последовательно откладывают 2 равных отрезка длиной 6 см. Полученный отрезок ОА является искомым, его длина: 2 ∙ 6 (см) = 12 (см). 2 способ. Находят длину второго отрезка: 2 ∙ 6 (см) = 12 (см), а затем строят два отрезка: один – длиной 6 см, а другой – длиной 12 (см).
Задача 3. Отрезок длиной 18 см разделите на две равные части. Решение. Поскольку не выделена операция деления длины отрезка на натуральное число, то мы воспользуется тем, что деление на натуральное число равносильно умножению ее на дробь 1n. В связи с этим получаем: 18 (см) : 2 = 18 см ∙ 12 = 8 ∙12 см = 9 см. Ответ: 9 см.
В заключение приводим таблицу мер длины. 1 сантиметр (см) = 10 миллиметрам (мм); 1 дециметр (дм) = 10 сантиметрам (см); 1 метр (м) = 10 дециметрам (дм) = 100 сантиметрам (см); 1 километр (км) = 1000 метрам (м).
Источник
Математика
6 класс
Урок № 75
Длина отрезка
Перечень рассматриваемых вопросов:
- длина отрезка;
- единицы измерения длины;
- способы измерения длины отрезка;
- решение задач на вычисление длины отрезка.
Тезаурус
Отрезок – это часть прямой, ограниченная двумя точками.
Длина отрезка – это расстояние между его концами.
Измерение длины отрезка – это сравнение длины отрезка с выбранной единицей измерения.
Длиной отрезка называется положительная величина, определённая для каждого отрезка.
Любой отрезок имеет определённую длину, большую нуля.
Обязательная литература:
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. – М.: Просвещение, 2017, стр. 258.
Дополнительная литература:
- Чулков П. В. Математика: тематические тесты.5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина – М.: Просвещение, 2009, стр. 142.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин – М.: Просвещение, 2014, стр. 95.
Теоретический материал для самостоятельного изучения
Что такое отрезок?
Отрезок – это часть прямой, ограниченная двумя точками.

Как отрезки обозначаются на чертежах?
Отрезок можно обозначить двумя заглавными буквами – отрезок АВ. Или можно обозначить отрезок одной строчной буквой – отрезок с.
Любой отрезок имеет определённую длину, большую нуля.

Длина может быть выражена натуральным или дробным числом.

Измерить отрезок – значит найти его длину.
Длина отрезка – это расстояние между его концами.
Свойства длин отрезков:
– равные отрезки имеют равные длины;
– если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.

Эти свойства длины отрезка используются при её измерении. Чтобы измерить длину отрезка, нужно выбрать единицу длины.
Такой единицей может быть длина произвольного отрезка. В мультфильме «38 попугаев» герои измеряли длину удава в попугаях.

Для определения длины отрезка надо узнать, сколько раз в данном отрезке помещается выбранная единица измерения.
Можно сравнивать длины отрезков, не имея под рукой линейки. Например, прикладывать к отрезкам один и тот же карандаш, ластик или использовать циркуль. Для этого нужно установить иглу в начало отрезка, провести дугу, пересекающую отрезок, затем, не меняя расстояния между иглой и карандашом циркуля, переставить иглу в точку пересечения и повторить действия.
В десятичной системе мер единицами измерения длины являются 1 мм, 1 см, 1 дм, 1 м и т. д.
Рассмотрим несколько примеров измерения длины отрезка. Измерения небольших отрезков удобно производить с помощью линейки.

Прикладываем линейку так, чтобы один конец отрезка совместился с нулём. Единичный отрезок 1 см отложился 7 раз, значит, длина отрезка АВ = 7 см.

Если единичный отрезок 1 см отложился n раз, и осталась часть меньшая 1 см, то откладываем отрезки равные 1/10 см. Длина отрезка СD = 8,7 см.
При необходимости можно продолжить откладывать по 1/100 части единичного отрезка и т. д.
Алгоритм измерения длины отрезков:
– выбрать какой-либо отрезок и принять его за единицу длины;
– от одного из концов отрезка отложить последовательно отрезки, равные единичному;
– если единичные отрезки отложились n раз и конец последнего совпал с концом измеряемого отрезка, то значение его длины равно n единиц длины;
– если отрезок или его часть меньше единичного отрезка, то нужно отложить отрезки, равные 1/10 части единичного отрезка;
– если десятые части единичного отрезка отложились ровно n раз, то длина измеряемого отрезка есть конечная десятичная дробь, в которой целая часть равна количеству целых единичных отрезков, а после запятой в разряде десятых стоит количество десятых частей единичного отрезка;
– при необходимости можно откладывать 1/100 часть единичного отрезка и т. д.
Таким образом, для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
И для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
На практике используют приближённое значение длин отрезков, например, с точностью 1/10 или 1/100 части единичного отрезка, но точность приближения зависит от поставленной задачи.
Рассмотрим фигуры, составленные из отрезков.
Возьмем на плоскости несколько точек и соединим их отрезками. Если никакие два из этих отрезков, имеющих общие точки, не лежат на одной прямой, то линию называют ломаной.
Отрезки, из которых состоит ломаная, называются звеньями, а концы этих отрезков – вершинами ломаной.
Длина ломаной – это сумма длин всех её звеньев.

Если концы ломаной совпадают, то такая ломаная называется замкнутой.
Замкнутая ломаная линия, у которой звенья не пересекаются между собой, называется многоугольником.

Периметр многоугольника равен сумме длин всех его сторон.
Разбор заданий тренировочного модуля
Тип 1. Ввод с клавиатуры пропущенных элементов в тексте.
Впишите верный ответ.
Точка P лежит на отрезке AB. Известно, что отрезок AP больше отрезка PB на 3,6 см, а отрезок AB = 10,4 см. Найдите длину отрезка PB.

Решение:
Пусть PB = x, тогда AP = x + 3,6 см.
По условию AB = 10,4 см.
Если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.
PB + AP = AB.
Составим и решим уравнение:
x + x + 3,6 = 10,4,
2x + 3,6 = 10,4,
2x = 10,4 – 3,6,
2x = 6,8,
x = 3,4.
Значит, длина отрезка PB = 3,4 см.
Ответ: 3,4 см.
Тип 2. Множественный выбор
Выберите верные ответы.
Задача 2
Известно, что отрезок AС = 3,6 см, а отрезок BС = 7,5 см. Найдите длину отрезка АB, если все три точки лежат на одной прямой.
Варианты ответов: 3,9; 11,2; 4,8; 13,2; 16,5; 2,9.
Первый вариант решения

В этом случае АВ = АС + ВС = 3,6 + 7,5 = 11,2 (см).
Второй вариант

BC = AB + AC,
АВ = ВС – АС = 7,5 – 3,6 = 3,9 (см).
Значит, длина отрезка АВ может быть равна 11,2 см или 3,9 см. Выбираем эти варианты.
Ответ: 11,2; 3,9.
Источник
- Главная
- Справочники
- Справочник по геометрии 7-9 класс
- Начальные геометрические сведения
- Длина отрезка
Отрезок – это геометрическая фигура, которая имеет начало и конец, значит отрезки можно измерять.
Измерить отрезок – значит найти его длину(расстояние между его концами).
Для того, чтобы найти длину отрезка, его сравнивают с отрезком принятым за единицу измерения, который носит название единичный отрезок.
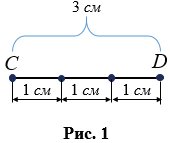
Если за единицу измерения принять сантиметр, то, чтобы определить длину отрезка, нужно узнать сколько раз в этом отрезке укладывается сантиметр. На рис.1 в отрезке СD сантиметр укладывается ровно три раза, значит, длина отрезка СD равна 3 см, можно записать СD = 3 см. В данном случае, для измерения удобно использовать сантиметровую линейку.
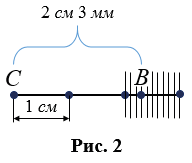
Бывает, что единичный отрезок не укладывается целое число раз в измеряемый отрезок, тогда единичный отрезок делят на 10 равных частей и определяют сколько раз одна десятая часть укладывается в остатке измеряемого отрезка. На рис.2 в отрезке СВ сантиметр укладывается 2 раза и в остатке 3 раза укладывается одна десятая часть сантиметра, значит, длина отрезка СВ равна 3,3 см или, учитывая что для сантиметра десятая часть равна миллиметру, 3 см 3 мм, т.е. можно записать СВ = 3,3 см (СВ = 3 см 3 мм).

Может получится так, что и в миллиметрах остаток не укладывается целое число раз, тогда:
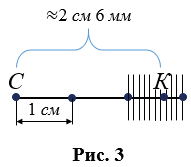
- Если нужны более точные измерения, то процесс деления продолжается, т.е. миллиметр также можно разделить на 10 равных частей и т.д. Такая точность в повседневной жизни не нужна, поэтому пользуются приближенными значениями, но имеет важную роль при проведении каких-либо исследований для совершения научных открытий.
За единицу измерения можно принимать не только сантиметр, но и другие отрезки, например, дециметр, метр и т.д.
Длина отрезка – это всегда какое-то положительное число.
Свойства длин отрезков:
- Равные отрезки имеют равные длины.
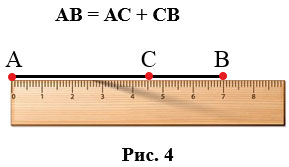
- Если точка делит отрезок на два отрезка, то длина всего отрезка равна сумме длин этих двух отрезков. Так на Рис.4 точка С делит отрезок АВ на два отрезка АС и СВ. Приложим линейку и видим, что АС = 4,5 см, СВ = 2,5 см, АВ = 7 см, т.е. АС + СВ = АВ.
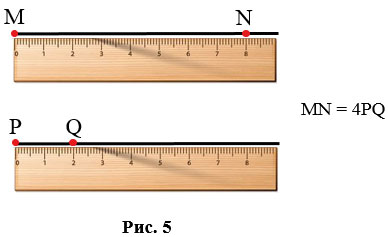
- Если длина одного отрезка MN в n раз больше длины другого отрезка PQ, то записывают MN = nPQ. На Рис.5 даны два отрезка MN и PQ, приложим к ним линейку и видим, что MN = 8 см, PQ = 2 см, т.е. MN больше PQ в 4 раза, тогда можно записать, что MN = 4PQ.
Поделись с друзьями в социальных сетях:
Советуем посмотреть:
Точки, прямые, отрезки
Провешивание прямой на местности
Луч
Угол
Равенство геометрических фигур
Сравнение отрезков
Сравнение углов
Единицы измерения длины, расстояний
Градусная мера угла
Измерение углов на местности
Смежные углы
Вертикальные углы
Перпендикулярные прямые
Построение прямых углов на местности
Начальные геометрические сведения
Правило встречается в следующих упражнениях:
7 класс
Задание 24,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 30,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 34,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 36,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 38,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 12,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 78,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 98,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 1,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Задание 7,
Атанасян, Бутузов, Кадомцев, Позняк, Юдина, Учебник
Источник
В геометрии длина – это величина, характеризующая протяженность отрезка.
Определение. Длиной отрезка называется неотрицательная величина, обладающая следующими свойствами:
1) равные отрезки имеют равные длины;
2) если отрезок состоит из двух отрезков, то его длина равна сумме длин его частей.
Эти свойства длины отрезка используются при ее измерении. Чтобы измерить длину отрезка, нужно иметь единицу длины, такой единицей является длина произвольного отрезка. Результатом измерения длины отрезка х является неотрицательное действительное число, обозначим его т(х). Это число называют численным значением длины отрезка х при выбранной единице длины или просто длиной.
Такое число всегда существует и единственно. Для каждого положительного действительного числа существует отрезок, длина которого выражается этим числом.
Из определения длины отрезка следуют известные свойства численных значений длин. Сформулируем некоторые из них, считая, что единица длины выбрана.
1. Если два отрезка равны, то численные значения их длин также равны, и обратно: если численные значения длин двух отрезков равны, то равны и сами отрезки.
х = y <=> т(х) = т(у)
2. Если отрезок х состоит из отрезков х, и х2, то численное значение его длины равно сумме численных значений длин отрезков х, и х2. Справедливо и обратное утверждение.
х = х1 х2 <=> т(х) = т(х1) + т(х2)
3. При замене единицы длины численное значение длины увеличивается (уменьшается) во столько раз, во сколько новая единица меньше (больше) старой.
4. Численное значение длины единичного отрезка равно единицы.
Рассмотрим процесс измерение длин отрезков. Из множество отрезков выбирают какой – нибудь отрезок е и принимают его за единицу длины. На отрезке а от одного из его концов откладывают последовательно отрезки, равные е, до тех пор, пока это возможно. Если отрезки, равные е отложились п раз и конец последнего совпал с концом отрезка а, то говорят, что значение длины отрезка а есть натуральное число п, и пишут а = пе. Если же отрезки, равные е, отложились п раз и остался еще остаток, меньшее, то на нем откладывают отрезки равные е1= 1/10 ∙е. Если они отложились точно п1 раз, то тогда а = п1е и значение длины отрезка а есть конечная десятичная дробь. Если же отрезок е1отложился п1 раз и остался еще остаток, меньшей е1, то на нем откладывают отрезки равные е2 = 1/100 ∙ е. Если представить этот процесс бесконечно продолжительным, то получим, что значение длины отрезка а есть бесконечная десятичная дробь.
Итак, при выбранной единицы длина любого отрезка выражается положительными числами.
На практике для измерения длин отрезков используются различные инструменты, в частности линейка с нанесенными на ней единицами длины.
При решении практических задач используются стандартные единицы длины: миллиметр (мм), сантиметр (см), метр (м), километр (км) и др.
Соотношение между ними:
1 километр (км) = 1000 метрам (м)
1 метр (м) = 10 дециметрам (дм) = 100 сантиметрам (см)
1 дециметр (дм) = 10 сантиметрам (см)
1 сантиметр (см) = 10 миллиметрам (мм)
Дата добавления: 2015-04-18; просмотров: 385; Нарушение авторских прав
Источник
Математика
5 класс
Урок №22
Измерение отрезков
Перечень рассматриваемых вопросов:
– понятие длины отрезка;
– равные отрезки на чертежах;
– определение длины отрезков.
Тезаурус
Длина отрезка – число, которое показывает, сколько раз в отрезке содержится единичный отрезок.
Единичный отрезок – это отрезок, длина которого принята за единицу измерения.
Обязательная литература
Никольский С. М. Математика. 5 класс. Учебник для общеобразовательных учреждений. // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др.– М.: Просвещение, 2017. – 272 с.
Дополнительная литература
1. Чулков П. В. Математика: тематические тесты. 5 класс.// П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина. –М.: Просвещение, 2009. – 142с.
2. Шарыгин И. Ф. Задачи на смекалку: 5-6 классы. // И. Ф. Шарыгин, А. В. Шевкин. – М.: Просвещение, 2014. – 95с.
Теоретический материал для самостоятельного изучения
Каждому человеку неоднократно приходилось что-то измерять: свой рост, длину прыжка, высоту потолка и многое другое. Все эти действия означают вычисление величины какого-нибудь отрезка. Каким же образом можно измерить длину отрезка? На этот вопрос ответим в ходе урока.
За свою историю человечество придумало много разных единиц длины. Позже появились меры, заимствованные из природы:
– пядь – расстояние между растянутыми большим и указательным пальцами;
– вершок – длина основной фаланги указательного пальца;
– локоть – расстояние от локтевого сустава до конца вытянутого среднего пальца руки.
Некоторые названия сохранились до сих пор: ярд, фут, пядь, дюйм.
Ну, а герои одного известного мультфильма измеряли длину удава в попугаях. В зависимости от того, в ком измеряли удава, он становился то длиннее, то короче.
Два слонёнка, пять мартышек или тридцать восемь попугаев.
«А в попугаях я гораздо длиннее!» – воскликнул удав.
На самом деле мы с вами понимаем, что его размеры не менялись. Тогда возникает вопрос: в чём измерять? Что брать за единицу длины? Слонёнка, попугая или мартышку.
Измерить длину какого-нибудь отрезка в заданных единицах измерения – значит найти число, показывающее, сколько единичных отрезков поместится в данном отрезке.
Длиной отрезка называют число, которое показывает, сколько раз в отрезке содержится единица измерения.
Отрезок, длина которого принята за единицу измерения, называется единичным отрезком.
Чем же можно измерить длину отрезка?
Наиболее древними геометрическими инструментами являются линейка и циркуль, последний был изобретён в первом веке в Древней Греции.
Для более точных измерений используют миллиметровую линейку и штангенциркуль.
Если при измерении линейкой определённого отрезка какая-то точка не совпадает с делением шкалы, то можно говорить о приближенном значении длины этого отрезка. Приближенное значение длины может быть с избытком, с недостатком и с округлением. Например, на рисунке отрезок АВ может быть измерен с точностью до сантиметров. Его длину можно найти приближенно с избытком или с недостатком. В таких случаях говорят, что с недостатком его длина равна 5 см, а с избытком – 6 см. Это записывают так: АВ 5 см (с недостатком); АВ 6 см (с избытком).
Далее построим отрезок ВК заданной длины –например, 8см. Для этого отметим точку В и приложим к ней линейку, совместив точку В с нулём. Затем отмеряем с помощью линейки 8 см, отмечаем точку К и соединяем обе точки линией.

Такой отрезок можно построить и с помощью циркуля. Для этого отметим точку В. Приложим к линейке циркуль, выставив его ножки на восемь сантиметров. Перенесём циркуль к точке В, поместив на неё одну ножку, а другой ножкой поставим точку К. Соединив обе точки линией, получим отрезок с длиной 8 см.
Отрезки можно сравнить с помощью измерителя –например, циркуля. Для этого попеременно подставляем ножки циркуля ко всем предложенным для сравнения отрезкам. При этом они должны быть выставлены по одному из отрезков. Если длины отрезков одинаковы, то отрезки считают равными и пишут CD = КМ.
Если один из отрезков является частью другого, следовательно, он короче. Например, ЕН короче EF, так как отрезок EH является частью EF.

Рассмотрим ещё одно свойство длин.
Если на отрезке АВ отметить точку С, то длина отрезка АВ равна сумме длин отрезков АС и СВ. Пишут: АВ = АС + СВ.
Наши органы чувств – это один из способов получения информации об окружающем нас мире, но информация полученная таким образом, бывает искажена.
Посмотрите на рисунки и ответьте на вопрос, равны ли отрезки?
На первый взгляд покажется, что правый отрезок больше, чем левый, но при сравнении с помощью линейки окажется, что отрезки равны.

Такая же ситуация, складывается и со следующей картинкой. Кажется, что нижний отрезок больше, чем верхний, но при наложении линейки окажется, что отрезки равны.

В другом же случае на тот же вопрос о равенстве отрезков ответ очевиден.
АВ
СК
Таким образом, можно сделать вывод, что глазомерные оценки геометрических реальных величин неточны.
Разбор решения заданий тренировочного модуля
№1. Тип задания: выбор элемента из выпадающего списка.
Сравните длины горизонтального и вертикального отрезков?

- Отрезки равны
- Вертикальный отрезок больше
- Горизонтальный отрезок больше
Правильный ответ: при выполнении данного задания нужно использовать линейку, нужно измерить длину каждого отрезка и сравнить их. В результате измерений мы увидим, что отрезки равны.
№2. Тип задания: выделение цветом.
Точка К расположена на прямой между точками А и В. Длина отрезка АК = 8 см, длина отрезка КВ на 2 см больше длины отрезка АК. Какова длина отрезка АВ?
Выберите правильный ответ: 6 см; 10 см; 12 см; 18 см.
Решение: изобразим условие задачи на рисунке.

АВ = АК + КВ. Найдём КВ по условию задачи.
КВ = 8 см + 2 см = 10 см.
Следовательно, АВ = 8 см + 10 см = 18 см.
Источник
