Какие свойства у треугольника и четырехугольника

Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Математический справочник / / Математика для самых маленьких. Шпаргалки. Детский сад, Школа. / / Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. Свойства параллелограмма. Свойства ромба. Свойства прямоугольника. Свойства квадрата. Свойства трапеции. Примерно 7-9 класс (13-15 лет)
Свойства четырехугольников. Виды четырехугольников. Свойства произвольных четырехугольников. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Виды четырехугольников: | |||
| |||
| |||
| |||
| |||
|  | ||
Свойства произвольных четырехугольников: | |||
| 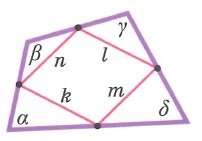 | ||
Свойства параллелограмма: | |||
| 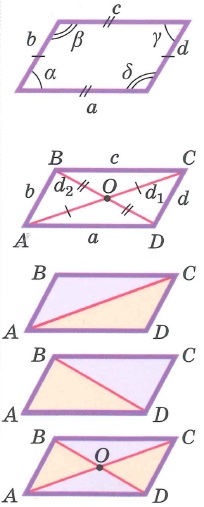 | ||
Свойства ромба: | |||
| 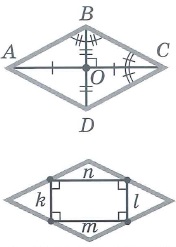 | ||
Свойства прямоугольника: | |||
| 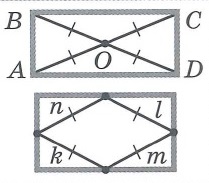 | ||
Свойства квадрата: | |||
| |||
Свойства трапеции: | |||
|  | ||
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Поиск в инженерном справочнике DPVA. Введите свой запрос:
Если Вы не обнаружили себя в списке поставщиков, заметили ошибку, или у Вас есть дополнительные численные данные для коллег по теме, сообщите , пожалуйста.
Вложите в письмо ссылку на страницу с ошибкой, пожалуйста.
Коды баннеров проекта DPVA.ru
Начинка: KJR Publisiers
Консультации и техническая
поддержка сайта: Zavarka Team
Free xml sitemap generator
Источник
В статье описываются геометрические фигуры: определение, основные свойства и формулы.
Плоские геометрические фигуры:
Четырехугольник (общее для всех четырехугольников)
Квадрат
Прямоугольник
Параллелограмм
Ромб
Трапеция
Треугольник
Окружность
Геометрические фигуры — это любое сочетание точек, линий и поверхностей. Геометрические фигуры разделяются на плоские и объемные.
Плоские геометрические фигуры — это фигуры, все точки которых лежат на одной плоскости. Объемные геометрические фигуры — это фигуры, не все точки которых лежат на одной плоскости.
Четырёхугольник
Четырёхугольник — это геометрическая фигура (многоугольник), состоящая из четырёх точек (вершин) и четырёх отрезков (сторон), которые последовательно соединяют вершины. При этом никакие три точки не лежат на одной прямой.
Основные свойства:
- Сумма углов четырёхугольника равна 360°
- Не существует четырёхугольников, у которых все углы острые или все углы тупые.
- Каждый угол четырёхугольника всегда меньше суммы трёх остальных углов.
- Каждая сторона четырёхугольника всегда меньше суммы трёх остальных сторон.
В четырёхугольник можно вписать окружность, если суммы его противолежащих сторон равны. Центр вписанной в четырёхугольник окружности является точкой пересечения биссектрис всех четырёх углов этого четырёхугольника.
Четырёхугольник можно описать окружностью, если сумма его противолежащих углов равна 180°.Центр описанной около четырёхугольника окружности является точкой пересечения всех четырёх серединных перпендикуляров сторон этого четырёхугольника.
Квадрат
Квадрат — правильный четырёхугольник, то есть четырёхугольник, у которого все углы равны и все стороны равны.
Основные формулы:
Периметр: P=4a, где P-периметр, a-сторона
Площадь: S=a2или S=d2/2
Сторона и диагональ связаны соотношениями: a=d/√2, d=a√2
Радиус описанной окружности: R=d или R=a/√(2)
Радиус вписанной окружности: r=a/2
где a-сторона, d-диагональ, P-периметр, S-площадь
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(2) – корень квадратный из 2.
Свойства:
- Все стороны равны, все углы равны и составляют 90°;
- Диагонали квадрата равны и перпендикулярны;
- У квадрата центры вписанной и описанной окружностей совпадают и находятся в точке пересечения его диагоналей;
- Квадрат является одновременно частным случаем ромба и прямоугольника.
Прямоугольник
Прямоугольник — четырехугольник, у которого все углы прямые.
Основные формулы:
Периметр: P=(a+b)*2
Площадь по сторонам: S = a*b
Площадь по диагонали и углу между ними: S = d²* sin γ. / 2
Стороны и диагональ связаны соотношением: d=√(a2+b2)/2 (теорема Пифагора)
Радиус описанной окружности: R= √(a2+b2)/2 (теорема Пифагора)
где a, b — длины сторон прямоугольника, d-диагональ, P-периметр, S-площадь
γ – угол между диагоналями
*Корень квадратный вычисляется из всего, что стоит в скобках после знака √, например, √(a2+b2) – корень квадратный из (a2+b2).
Свойства:
- Диагонали прямоугольника равны и делятся точкой пересечения пополам.
- Около любого прямоугольника можно описать окружность с центром в точке пересечения его диагоналей и радиусом, который равен половине диагонали.
Параллелограмм
Параллелограмм — четырёхугольник, у которого противоположные стороны попарно параллельны, то есть лежат на параллельных прямых.
Определения:
Высота параллелограмма — это перпендикуляр, проведённый из вершины параллелограмма к противоположной стороне.
Основные формулы:
Стороны и диагональ связаны соотношением: (d1)2+(d2)2=(a2+b2)*2
Периметр: P=(a+b)*2
Площадь по стороне и высоте: S = a*h
S (Площадь) по двум сторонам и углу между ними: S=a*b*sin α
S (Площадь) по двум диагоналям и углу между ними: S=(d1*d2)/2*sin γ
где a, b — длины сторон, d1, d2 –диагонали, P-периметр, S-площадь,
h-высота, проведенная к противоположной стороне
α — угол между сторонами параллелограмма,
γ — угол между диагоналями параллелограмма (острый).
Свойства:
- У параллелограмма противоположные стороны равны и противоположные углы равны.
- Сумма любых двух соседних углов параллелограмма равна 180°.
- Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.
- Каждая диагональ делит параллелограмм на два равных треугольника.
- Две диагонали параллелограмма делят его на четыре равновеликих треугольника (равны площади всех 4-х треугольников)
- Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.
- Частными случаями параллелограмма являются прямоугольник, квадрат и ромб.
Ромб
Ромб — это параллелограмм, у которого все стороны равны.
Основные формулы:
Периметр: P=4*a
Площадь по стороне и высоте: S=a*h
Площадь по диагоналям: S = (d1*d2)/2
Радиус окружности, вписанной в ромб: r=h/2 или r =(d1*d2)/4a
Площадь по стороне и радиусу вписанной окружности: S=2*a*r
Площадь по стороне и углу: S = a2 · sin α
где a — длина стороны, d1, d2 –диагонали, P-периметр, S-площадь,
h -высота, проведенная к противоположной стороне
α — угол между сторонами ромба
Свойства:
- Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.
- В любой ромб можно вписать окружность с центром в точке пересечения его диагоналей. Радиус окружности: r=h/2 или r = d1*d2/4a.
Трапеция
Трапеция — четырёхугольник, у которого только две противолежащие стороны параллельны.
Определения:
- Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.
- Высота трапеции – перпендикуляр, проведённый из произвольной точки одного основания трапеции к прямой, содержащей другое основание трапеции.
- Средняя линия (первая средняя линия) трапеции — отрезок, который соединяет середины боковых сторон данной трапеции.Средняя линия трапеции параллельна её основаниям и равна их полусумме.
- Средняя линия (вторая средняя линия) — отрезок, соединяющий середины оснований, проходит через точку пересечения диагоналей.
- Равнобокая трапеция – трапеция,у которой боковые стороны равны (c=d). У равнобокой трапеции:диагонали равны, углы при основании равны, сумма противолежащих углов равна 180°.Около трапеции можно описать окружность тогда и только тогда, когда она равнобокая.
- Прямоугольная трапеция — трапеция, у которой одна из её боковых сторон перпендикулярна основаниям.
Основные формулы:
Периметр: P=a+b+c+d
Площадь определить: S=h*(a+b)/2
Стороны и диагональ равнобокой трапеции: d² = ab+c²
Радиус вписанной окружности: r = h/2
где a,b — основания, c,d — боковые стороны (с – боковые стороны в случае, если трапеция равнобокая), d1, d2 –диагонали,
P-периметр, S-площадь, h -высота, проведенная к противоположной стороне
Свойства:
В трапецию можно вписать окружность, если сумма её основ равна сумме боковых сторон (a+b=c+d). Центром вписанной в трапецию окружности является точка пересечения биссектрис внутренних углов трапеции.
Треугольник
Треугольник – это геометрическая фигура, которая состоит из трёх точек, не лежащих на одной прямой (вершин треугольника) и трёх отрезков с концами в этих точках (сторон треугольника).
Определения:
- Углами (внутренними углами) треугольника называются три угла, каждый из которых образован лучами, выходящими из вершин треугольника и проходящими через две другие вершины.
- Высота треугольника — перпендикуляр, опущенный из любой вершины треугольника на противолежащую сторону или на продолжение стороны
- Медиана треугольника — отрезок, который соединяет вершину треугольника с серединой противолежащей стороны.
- Биссектрисой треугольника, проведённой из данной вершины, называется отрезок биссектрисы угла треугольника, соединяющий эту вершину с точкой на противолежащей стороне
- Равные треугольники – треугольники, у которых соответствующие стороны равны и соответствующие углы равны
- Равнобедренный треугольник— треугольник, у которого две стороны равны. Равные стороны называют боковыми сторонами, а третью – основанием равнобедренного треугольника.
- Равносторонний или правильный треугольник – треугольник, у которого все стороны равны.
- Прямоугольный треугольник — треугольник, у которого есть прямой угол. Стороны, прилежащие к прямому углу, называются катетами, противолежащая прямому углу – гипотенузой.
Основные формулы:
Периметр: P=a+b+c
Площадь по стороне и высоте: S=(a*h)/2
Площадь: по сторонам и углу между ними: S=(a*b)/2* sin γ
по трем сторонам и радиусу описанной окружности: S=(a*b*c)/4R
по трем сторонам и радиусу вписанной окружности: S=(a+b+c)/2*r
Площадь прямоугольного треугольника: S=(a*b)/2
Стороны прямоугольного треугольника: c2=a2+b2 (Теорема Пифагора)
где a,b, c — стороны (a,b –катеты , с – гипотенуза в случае прямоугольного треугольника)
d1, d2 –диагонали, h -высота, проведенная к противоположной стороне,
P-периметр, S-площадь, γ — угол между сторонами a и b
r — радиус вписанной окружности, R — радиус описанной окружности
Свойства:
- В треугольнике против большего угла лежит большая сторона, против большей стороны лежит больший угол.
- Сумма углов треугольника равна 180°:
- Длина каждой стороны треугольника больше разности и меньше суммы длин двух других сторон: |a-b| <c<a+b
- Высоты треугольника пересекаются в одной точке, которая называется ортоцентром треугольника.
- Медиана делит треугольник на два равновеликих (с равными площадями) треугольника. Три медианы треугольника делят его на шесть равновеликих треугольников
- Биссектрисы внутренних углов треугольника пересекаются в одной точке, находящейся внутри треугольника, равноудалённой от трёх его сторон, которая является центром окружности, вписанной в данный треугольник
- В равнобедренном треугольнике углы при основании равны. В равнобедренном треугольнике медиана, проведённая к основанию, является и биссектрисой и высотой.
- Все углы равностороннего треугольника равны 60°. Каждая медиана равностороннего треугольника совпадает с биссектрисой и высотой.
- В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: c2=a2+b2 (Теорема Пифагора).В прямоугольном треугольнике гипотенуза всегда больше любого из катетов.
Окружность
Окружность — замкнутая плоская кривая, все точки которой одинаково удалены от данной точки (центра окружности), которая лежит в той же плоскости, что и кривая.
Определения:
- Радиус — отрезок, который соединяет центр окружности с любой её точкой.
- Хорда — отрезок, который соединяет какие-либо две точки окружности (AB).
- Диаметр — хорда, проходящая через центр окружности(d). Диаметр – наибольшая хорда окружности. Наименьшей хорды окружности не существует.
- Касательная — прямая, которая лежит в одной плоскости с окружностью и имеет с ней только одну общую точку (E)
- Секущая — прямая, которая пересекает окружность в двух различных точках.
Основные формулы:
Длина окружности: L = 2πR
Площадь круга: S = π*r2 или S = π*d2/4
где π = 3,14 (3,1415926535) – величина постоянная,
где r-радиус, d –диаметр, L – длина окружности, S-площадь.
Источник
Участник конкурса «Методическая шкатулка 2010»
Огарцева Наталья Владимировна,учитель начальных классов
высшей категории МОУ « СОШ №27 с углубленным изучением отдельных предметов» г. Балаково
Саратовской области.
Содержание
«Свойства четырехугольников и треугольников»
3 класс
Краткое описание занятия.
На конкурс «Методическая шкатулка 2010» в номинации «Урок с использованием цифровых образовательных ресурсов» я представляю конспект урока по математике по теме «Свойства четырехугольников и треугольников. Обобщение» и презентацию к уроку для учащихся 3 класса. Цель занятия – обобщить знания о свойствах четырехугольников: квадрате, прямоугольнике, ромбе, трапеции, научить узнавать эти фигуры в окружающих нас предметах. Учить учащихся различать треугольники по их свойствам и признакам, находить площадь прямоугольника и других фигур. Внеклассное мероприятие проводится интегрировано с уроком трудового обучения. Учащиеся делают аппликации города Четырехугольников и Треугольников, где жители, дома и окружающие предметы состоят из треугольников или четырехугольников. В качестве закрепления я провожу игру «Брейн – ринг».
Слайды, которые я использую, позволяют наглядно и занимательно научить учащихся узнавать и отличать каждый вид четырехугольника, быстро переключаться с одного задания на другое и находить правильное решение. Применение ИКТ также способствует развитию навыков контроля и самоконтроля. Проверка работы по эталону осуществляется легко и быстро, если это предусмотрено в презентационном сопровождении. Наглядность материала повышает его усвоение, т.к. задействованы все каналы восприятия учащихся – зрительный, механический, слуховой и эмоциональный.
Фрагменты этого урока учителя начальных классов могут использовать на уроках математики при изучении темы «Квадрат», «Прямоугольник», «Виды треугольников» в 3 классе. Логические задачи и упражнения можно использовать в математических олимпиадах и КВН в начальной школе.
Цель:
- Обобщить знания о свойствах четырехугольников и треугольников, решать задачи на нахождение площади прямоугольника и других фигур. Решать задачи на построение.
- Развивать логику, мышление , интерес к предмету.
- Воспитывать взаимовыручку, чувство коллективизма.
=== Оборудование: === компьютер,мультимедийный проектор, презентация урока, геометрические фигуры, аппаратура для игры «Брейн-ринг», плакаты, цветная бумага, ножницы.
=== Используемые ресурсы Единой коллекции цифровых образовательных ресурсов=== (https://school-collection.edu.ru):
Меры площади (N 167244),
Вычисление площади прямоугольника (N 167245),
Что знаем по геометрии (N 192268)
Ход урока.
- 1.Организация класса.
- 2.Сообщение цели и темы урока.
Мы с вами изучаем на математическом кружке раздел геометрии, но что мы знаем о возникновении этой науки?
- Слайд № 1. Эвклид.
Информация о возникновении геометрии.
Сегодня на уроке мы повторим свойства четырехугольников и треугольников.
- Слайд № 2. Четырехугольники и треугольники.
Как обычно мы начинаем занятие с игры «Запомни». Вы увидите фигуру, за 5секунд вы должны ее запомнить и нарисовать у себя в тетради.
- Слайд № 3.Запомни.
- Слайд № 4. Проверь.
Какие фигуры лежат в основе этих рисунков?
Сегодня у нас состоится съезд геометрических фигур.
- Слайд № 5. Съезд геометрических фигур.
А вот какие геометрические фигуры к нам прибудут – мы сейчас увидим: *Квадрат:
Он давно знаком со мной
Каждый угол в нем – прямой,
Все четыре стороны
Одинаковой длины
Вам его представить рад
А зовут его (квадрат)
- Прямоугольник:
Четыре сторонки, четыре угла
Четыре вершинки – вот и я!
У меня все углы прямые,
А противоположные стороны равны.
- Ромб:
У ромба стороны равны, а углы разные, два противоположных – острые, а два др.- тупые.
- Трапеция:
Трапеция больше на крышу похожа,
Юбку рисуют трапецией тоже
Взять треугольник и верх удалить,
Трапецию можно и так получить.
-А какое свойство трапеции вы знаете? (Две противоположные стороны параллельны)
- Параллелограмм:
Все вы слыхали шум и гам,
В чем дело, что случилось?
Прямоугольник раздавили там!
Он зваться стал параллелограмм!
-Что вы можете сказать о его сторонах? (У пар-ма противоположные стороны параллельны).
-Перед нами четырехугольники, а какие признаки сходства четырехугольников вы знаете?
- Слайд № 6. Признаки сходства четырехугольников.
А можно ли назвать квадрат прямоугольником? Почему?
- Слайд № 7. Признаки сходства квадрата и прямоугольника.
А в чем отличие?
- Слайд №8.Выпиши номера фигур, которые являются:1)четырехугольниками,2)прямоугольниками.
Задача №1
- Слайд № 8. Задача.
Найдите площадь прямоугольника со сторонами 2см и 5 мм
Задача № 2.
- Слайд № 9. Найдите площадь заштрихованной фигуры.
- Слайд №10. Посчитай сколько квадратов на чертеже? А прямоугольников?
-Какая-то ссора произошла между фигурами.
- Сценка «Квадрат и Треугольник».
Треугольник с Квадратом.
Старший квадратный,
Добродушный, приятный
Младший – треугольный,
Вечно недовольный.
Стал расспрашивать квадрат:
-Почему ты злишься, брат?
Тот кричит ему:- Смотри,
Ты полней меня и шире,
У меня углов лишь три,
У тебя же их четыре.
Но квадрат ответил:
-Брат!
Я же старше, я – квадрат.
И скажу тебе нежней:
Неизвестно, кто важней.
Но настала ночь, и к брату,
Натыкаясь на столы,
Младший лезет воровато
Срезать старшему углы.
Уходя, сказал:
-Приятных я тебе желаю снов.
Спать ложился ты квадратным,
А проснешься без углов.
Но на утро младший брат
Страшной мести был не рад.
Поглядел он – нет квадрата.
Онемел. Стоял без слов…
Вот так месть – теперь у брата
Восемь новеньких углов.
-Скажите, какая в геометрии самая важная фигура? Для чего мы изучаем
геометрию?
- Слайд № 10. Геометрия вокруг нас.
-А вот еще команда прибыла на съезд.
Треугольник:
Ты на меня, ты на него,
На всех нас посмотри,
У нас всего, у нас всего,
У нас всего по три!
Три стороны и три угла
И столько же вершин
И трижды трудные дела,
Мы трижды совершим.
Все в нашем городе друзья,
Дружнее не сыскать,
Мы треугольников семья,
Нас каждый должен знать!
Узнает очень просто меня любой дошкольник,
Я тупо-прямо-острый угольный треугольник.
- Слайд № 11. Виды треугольников.
-Назовите среди этих треугольников: остроугольный, прямоугольный и тупоугольный. Название треугольника зависит от угла начальника.
Задача на построение: постройте с помощью транспортира первый треугольник с углом градусной меры 50градусов.
второй с градусной мерой 120.
- Вывод:
прямой угол у прямоугольного треугольника равен 90 градусам.
острый угол – меньше 90,
тупой угол – больше 90.
.-А теперь мы устроим соревнование между нашими гостями – фигурами, и учениками.
- Игра «Брейн- ринг».
- Замкнутая ломаная из трех звеньев.
- Текст, в котором есть условие и вопрос.
- Какой прибор применяют для того, чтобы начертить окружность?
- Сумма длин сторон многоугольника – это…
- Четыре угла прямых, четыре равные стороны – это…
- Треугольник с отрезанной вершиной.
- Как называется отрезок, соединяющий противоположные вершины прямоугольника?
- Каким прибором измеряют градусную меру угла?
- Чему равен прямой угол?
- Чем отличается отрезок от луча?
- Сколько в одном кв. дециметре кв. миллиметров?
- Чем отличается квадрат от прямоугольника?
- Сколько радиусов содержится в диаметре?
Изготовление аппликаций городов Треугольников и Четырехугольников.
(Повторение правил по технике безопасности работы с ножницами).
Одна команда делает аппликацию города Треугольников, где дома,
деревья, жители состоят из треугольников, другая команда – аппликацию города Четырехугольников.
Итог урока
- Назовите фигуры, которые вы изобразили на своих полотнах?
- Что вам понравилось больше всего?
Используемая литература:
- Жильцова Т.В., Обухова Л.А. Поурочные разработки по наглядной геометрии. М.; ВАКО, 2004.
- Удодова Н.И. Занимательная математика. Волгоград: Учитель, 2008.
- Подгорная С. Н., Перекатьева О.В. Тематические недели в начальной школе. М.;ИКЦ «МарТ», Ростов н/Д,2004.
- Яровая Л.Н., Жиренко О.Е.Внеклассные мероприятия, 4-й класс. М.; ВАКО, 2005.
Источник
