Какие свойства у степени n
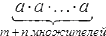
Ранее мы уже говорили о том, что такое степень числа. Она имеет определенные свойства, полезные в решении задач: именно их и все возможные показатели степени мы разберем в этой статье. Также мы наглядно покажем на примерах, как их можно доказать и правильно применить на практике.
Свойства степени с натуральным показателем
Вспомним уже сформулированное нами ранее понятие степени с натуральным показателем: это произведение n-ного количества множителей, каждый из которых равен а. Также нам понадобится вспомнить, как правильно умножать действительные числа. Все это поможет нам сформулировать для степени с натуральным показателем следующие свойства:
Определение 1
1. Главное свойство степени: am·an=am+n
Можно обобщить до: an1·an2·…·ank=an1+n2+…+nk.
2. Свойство частного для степеней, имеющих одинаковые основания: am:an=am−n
3. Свойство степени произведения: (a·b)n=an·bn
Равенство можно расширить до: (a1·a2·…·ak)n=a1n·a2n·…·akn
4. Свойство частного в натуральной степени: (a:b)n=an:bn
5. Возводим степень в степень: (am)n=am·n,
Можно обобщить до:(((an1)n2)…)nk=an1·n2·…·nk
6. Сравниваем степень с нулем:
- если a>0, то при любом натуральном n, an будет больше нуля;
- при a, равном 0, an также будет равна нулю;
- при a<0 и таком показателе степени, который будет четным числом 2·m, a2·m будет больше нуля;
- при a <0 и таком показателе степени, который будет нечетным числом 2·m−1, a2·m−1 будет меньше нуля.
7. Равенство an<bn будет справедливо для любого натурального n при условии, что a и b больше нуля и не равны друг другу.
8. Неравенство am>an будет верным при условии, что m и n – натуральные числа, m больше n и а больше нуля и не меньше единицы.
В итоге мы получили несколько равенств; если соблюсти все условия, указанные выше, то они будут тождественными. Для каждого из равенств, например, для основного свойства, можно поменять местами правую и левую часть: am·an=am+n – то же самое, что и am+n=am·an. В таком виде оно часто используется при упрощении выражений.
Далее мы разберем каждое свойство подробно и попробуем привести доказательства.
1. Начнем с основного свойства степени: равенство am·an=am+n будет верным при любых натуральных m и n и действительном a. Как доказать это утверждение?
Основное определение степеней с натуральными показателями позволит нам преобразовать равенство в произведение множителей. Мы получим запись такого вида:
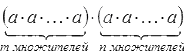
Это можно сократить до 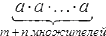 (вспомним основные свойства умножения). В итоге мы получили степень числа a с натуральным показателем m+n. Таким образом, am+n, значит, основное свойство степени доказано.
(вспомним основные свойства умножения). В итоге мы получили степень числа a с натуральным показателем m+n. Таким образом, am+n, значит, основное свойство степени доказано.
Разберем конкретный пример, подтверждающий это.
Пример 1
Итак, у нас есть две степени с основанием 2. Их натуральные показатели – 2 и 3 соответственно. У нас получилось равенство: 22·23=22+3=25 Вычислим значения, чтобы проверить верность этого равенства.
Выполним необходимые математические действия: 22·23=(2·2)·(2·2·2)=4·8=32 и 25=2·2·2·2·2=32
В итоге у нас вышло: 22·23=25. Свойство доказано.
В силу свойств умножения мы можем выполнить обобщение свойства, сформулировав его в виде трех и большего числа степеней, у которых показатели являются натуральными числами, а основания одинаковы. Если обозначить количество натуральных чисел n1, n2 и др. буквой k, мы получим верное равенство:
an1·an2·…·ank=an1+n2+…+nk.
Пример 2
Пример с конкретными числами (легко посчитать самостоятельно): (2,1)3·(2,1)3·(2,1)4·(2,1)7=(2,1)3+3+4+7=(2,1)17.
2. Далее нам необходимо доказать следующее свойство, которое называется свойством частного и присуще степеням с одинаковыми основаниями: это равенство am:an=am−n, которое справедливо при любых натуральным m и n (причем m больше n) ) и любом отличном от нуля действительном a.
Для начала поясним, каков именно смысл условий, которые упомянуты в формулировке. Если мы возьмем a, равное нулю, то в итоге у нас получится деление на нуль, чего делать нельзя (ведь 0n=0). Условие, чтобы число m обязательно было больше n, нужно для того, чтобы мы могли удержаться в рамках натуральных показателей степени: вычтя n из m, мы получим натуральное число. Если условие не будет соблюдено, у нас получится отрицательное число или ноль, и опять же мы выйдем за пределы изучения степеней с натуральными показателями.
Теперь мы можем перейти к доказательству. Из ранее изученного вспомним основные свойства дробей и сформулируем равенство так:
am−n·an=a(m−n)+n=am
Из него можно вывести: am−n·an=am
Вспомним про связь деления и умножения. Из него следует, что am−n– частное степеней am и an. Это и есть доказательство второго свойства степени.
Пример 3
Подставим конкретные числа для наглядности в показатели, а основание степени обозначим π: π5:π2=π5−3=π3
3. Следующим мы разберем свойство степени произведения: (a·b)n=an·bn при любых действительных a и b и натуральном n.
Согласно базовому определению степени с натуральным показателем мы можем переформулировать равенство так:
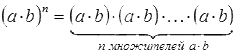
Вспомнив свойства умножения, запишем: 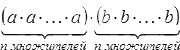 . Это значит то же самое, что и an·bn.
. Это значит то же самое, что и an·bn.
Пример 4
23·-4254=234·-4254
Если множителей у нас три и больше, то это свойство также распространяется и на этот случай. Введем для числа множителей обозначение k и запишем:
(a1·a2·…·ak)n=a1n·a2n·…·akn
Пример 5
С конкретными числами получим следующее верное равенство: (2·(-2,3)·a)7=27·(-2,3)7·a
4. После этого мы попробуем доказать свойство частного: (a:b)n=an:bn при любых действительных a и b, если b не равно 0, а n – натуральное число.
Для доказательства можно использовать предыдущее свойство степени. Если (a:b)n·bn=((a:b)·b)n=an , а (a:b)n·bn=an, то из этого выходит, что (a:b)n есть частное от деления an на bn.
Пример 6
Подсчитаем пример: 312:-0.53=3123:(-0,5)3
5. Далее мы поговорим о свойстве возведения степени в степень: (am)n=am·n для любого действительного a и любых натуральных n и m.
Пример 7
Начнем сразу с примера: (52)3=52·3=56
А теперь сформулируем цепочку равенств, которая докажет нам верность равенства: 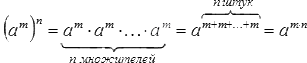
Если у нас в примере есть степени степеней, то это свойство справедливо для них также. Если у нас есть любые натуральные числа p, q, r, s, то верно будет:
apqys=ap·q·y·s
Пример 8
Добавим конкретики: (((5,2)3)2)5=(5,2)3·2·5=(5,2)30
6. Еще одно свойство степеней с натуральным показателем, которое нам нужно доказать, – свойство сравнения.
Для начала сравним степень с нулем. Почему an>0 при условии, что а больше 0?
Если умножить одно положительное число на другое, то мы получим также положительное число. Зная этот факт, мы можем сказать, что от числа множителей это не зависит – результат умножения любого числа положительных чисел есть число положительное. А что же такое степень, как не результат умножения чисел? Тогда для любой степени an с положительным основанием и натуральным показателем это будет верно.
Пример 9
35>0, (0,00201)2>0 и 3491351>0
Также очевидно, что степень с основанием, равным нулю, сама есть ноль. В какую бы степень мы не возводили ноль, он останется им.
Пример 10
03=0 и 0762=0
Если основание степени – отрицательное число, тот тут доказательство немного сложнее, поскольку важным становится понятие четности/нечетности показателя. Возьмем для начала случай, когда показатель степени четный, и обозначим его 2·m, где m – натуральное число.
Тогда:
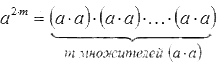
Вспомним, как правильно умножать отрицательные числа: произведение a·a равно произведению модулей, а, следовательно, оно будет положительным числом. Тогда 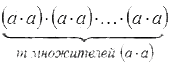 и степень a2·m также положительны.
и степень a2·m также положительны.
Пример 11
Например, (−6)4>0, (−2,2)12>0 и -296>0
А если показатель степени с отрицательным основанием – нечетное число? Обозначим его 2·m−1.
Тогда 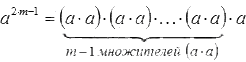
Все произведения a·a, согласно свойствам умножения, положительны, их произведение тоже. Но если мы его умножим на единственное оставшееся число a, то конечный результат будет отрицателен.
Тогда получим: (−5)3<0, (−0,003)17<0 и -111029<0
7. Далее разберем следующее свойство, формулировка которого такова: из двух степеней, имеющих одинаковый натуральный показатель, больше та, основание которой больше (и наоборот).
Как это доказать?
an<bn– неравенство, представляющее собой произведение левых и правых частей nверных неравенств a<b. Вспомним основные свойства неравенств справедливо и an<bn.
Пример 12
Например, верны неравенства: 37<(2,2)7 и 3511124>(0,75)124
8. Нам осталось доказать последнее свойство: если у нас есть две степени, основания которых одинаковы и положительны, а показатели являются натуральными числами, то та из них больше, показатель которой меньше; а из двух степеней с натуральными показателями и одинаковыми основаниями, большими единицы, больше та степень, показатель которой больше.
Докажем эти утверждения.
Для начала нам нужно убедиться, что am<an при условии, что m больше, чем n, и а больше 0, но меньше 1.Теперь сравним с нулем разность am−an
Вынесем an за скобки, после чего наша разность примет вид an·(am−n−1). Ее результат будет отрицателен (поскольку отрицателен результат умножения положительного числа на отрицательное). Ведь согласно начальным условиям, m−n>0, тогда am−n−1–отрицательно, а первый множитель положителен, как и любая натуральная степень с положительным основанием.
У нас вышло, что am−an<0 и am<an. Свойство доказано.
Осталось привести доказательство второй части утверждения, сформулированного выше: am>a справедливо при m>n и a>1. Укажем разность и вынесем an за скобки: (am−n−1).Степень an при а, большем единицы, даст положительный результат; а сама разность также окажется положительна в силу изначальных условий, и при a>1 степень am−n больше единицы. Выходит, am−an>0 и am>an, что нам и требовалось доказать.
Пример 13
Пример с конкретными числами: 37>32
Основные свойства степеней с целыми показателями
Для степеней с целыми положительными показателями свойства будут аналогичны, потому что целые положительные числа являются натуральными, а значит, все равенства, доказанные выше, справедливы и для них. Также они подходят и для случаев, когда показатели отрицательны или равны нулю (при условии, что само основание степени ненулевое).
Таким образом, свойства степеней такие же для любых оснований a и b (при условии, что эти числа действительны и не равны 0) и любых показателей m и n (при условии, что они являются целыми числами). Запишем их кратко в виде формул:
Определение 2
1. am·an=am+n
2. am:an=am−n
3. (a·b)n=an·bn
4. (a:b)n=an:bn
5. (am)n=am·n
6. an<bn и a−n>b−n при условии целого положительного n, положительных a и b, a<b
7. am<an, при условии целых m и n, m>n и 0<a<1, при a>1 am>an.
Если основание степени равно нулю, то записи am и an имеют смысл только лишь в случае натуральных и положительных m и n. В итоге получим, что формулировки выше подходят и для случаев со степенью с нулевым основанием, если соблюдаются все остальные условия.
Доказательства этих свойств в данном случае несложные. Нам потребуется вспомнить, что такое степень с натуральным и целым показателем, а также свойства действий с действительными числами.
Разберем свойство степени в степени и докажем, что оно верно и для целых положительных, и для целых неположительных чисел. Начнем с доказательства равенств (ap)q=ap·q, (a−p)q=a(−p)·q, (ap)−q=ap·(−q) и (a−p)−q=a(−p)·(−q)
Условия: p=0 или натуральное число; q– аналогично.
Если значения p и q больше 0, то у нас получится (ap)q=ap·q. Схожее равенство мы уже доказывали раньше. Если p=0, то:
(a0)q=1q=1 a0·q=a0=1
Следовательно, (a0)q=a0·q
Для q=0 все точно так же:
(ap)0=1 ap·0=a0=1
Итог: (ap)0=ap·0.
Если же оба показателя нулевые, то (a0)0=10=1 и a0·0=a0=1, значит, (a0)0=a0·0.
Далее разберем равенство (a−p)q=a(−p)·q. Согласно определению степени с целым отрицательным показателем имеем a-p=1ap, значит, (a-p)q=1apq.
Вспомним доказанное выше свойство частного в степени и запишем:
1apq=1qapq
Если 1p=1·1·…·1=1 иapq=ap·q, то 1qapq=1ap·q
Эту запись мы можем преобразовать в силу основных правил умножения в a(−p)·q.
Так же: ap-q=1(ap)q=1ap·q=a-(p·q)=ap·(-q).
И (a-p)-q=1ap-q=(ap)q=ap·q=a(-p)·(-q)
Остальные свойства степени можно доказать аналогичным образом, преобразовав имеющиеся неравенства. Подробно останавливаться мы на этом не будем, укажем только сложные моменты.
Доказательство предпоследнего свойства: вспомним, a−n>b−n верно для любых целых отрицательных значений nи любых положительных a и b при условии, что a меньше b.
Тогда неравенство можно преобразовать следующим образом:
1an>1bn
Запишем правую и левую части в виде разности и выполним необходимые преобразования:
1an-1bn=bn-anan·bn
Вспомним, что в условии a меньше b, тогда, согласно определению степени с натуральным показателем: – an<bn, в итоге: bn−an>0.
an·bn в итоге дает положительное число, поскольку его множители положительны. В итоге мы имеем дробь bn-anan·bn, которая в итоге также дает положительный результат. Отсюда 1an>1bn откуда a−n>b−n, что нам и нужно было доказать.
Последнее свойство степеней с целыми показателями доказывается аналогично свойству степеней с показателями натуральными.
Основные свойства степеней с рациональными показателями
В предыдущих статьях мы разбирали, что такое степень с рациональным (дробным) показателем. Их свойства такие же, что и у степеней с целыми показателями. Запишем:
Определение 3
1. am1n1·am2n2=am1n1+m2n2 при a>0, а если m1n1>0 и m2n2>0, то при a≥0 ( свойство произведения степеней с одинаковыми основаниями).
2.am1n1:bm2n2=am1n1-m2n2 , если a>0 (свойство частного).
3. a·bmn=amn·bmn при a>0 и b>0, а если m1n1>0 и m2n2>0, то при a≥0 и (или) b≥0 (свойство произведения в дробной степени).
4. a:bmn=amn:bmn при a>0 и b>0, а если mn>0, то при a≥0 и b>0 (свойство частного в дробной степени).
5. am1n1m2n2=am1n1·m2n2 при a>0, а если m1n1>0 и m2n2>0, то при a≥0 (свойство степени в степени).
6. ap<bp при условии любых положительных a и b, a<b и рациональном p при p>0; если p<0 – ap>bp (свойство сравнения степеней с равными рациональными показателями).
7. ap<aq при условии рациональных чисел p и q, p>q при 0<a<1; если a>0 – ap>aq
Для доказательства указанных положений нам понадобится вспомнить, что такое степень с дробным показателем, каковы свойства арифметического корня n-ной степени и каковы свойства степени с целыми показателем. Разберем каждое свойство.
Согласно тому, что из себя представляет степень с дробным показателем, получим:
am1n1=am1n1 и am2n2=am2n2, следовательно, am1n1·am2n2=am1n1·am2n2
Свойства корня позволят нам вывести равенства:
am1·m2n1·n2·am2·m1n2·n1=am1·n2·am2·n1n1·n2
Из этого получаем: am1·n2·am2·n1n1·n2=am1·n2+m2·n1n1·n2
Преобразуем:
am1·n2·am2·n1n1·n2=am1·n2+m2·n1n1·n2
Показатель степени можно записать в виде:
m1·n2+m2·n1n1·n2=m1·n2n1·n2+m2·n1n1·n2=m1n1+m2n2
Это и есть доказательство. Второе свойство доказывается абсолютно так же. Запишем цепочку равенств:
am1n1: am2n2=am1n1: am2n2=am1·n2:am2·n1n1·n2==am1·n2-m2·n1n1·n2=am1·n2-m2·n1n1·n2=am1·n2n1·n2-m2·n1n1·n2=am1n1-m2n2
Доказательства остальных равенств:
a·bmn=(a·b)mn=am·bmn=amn·bmn=amn·bmn;(a:b)mn=(a:b)mn=am:bmn==amn:bmn=amn:bmn;am1n1m2n2=am1n1m2n2=am1n1m2n2==am1m2n1n2=am1·m2n1n2==am1·m2n2·n1=am1·m2n2·n1=am1n1·m2n2
Следующее свойство: докажем, что для любых значений a и b больше 0, если а меньше b, будет выполняться ap<bp, а для p больше 0 – ap>bp
Представим рациональное число p как mn. При этом m–целое число, n–натуральное. Тогда условия p<0 и p>0 будут распространяться на m<0 и m>0. При m>0 и a<b имеем (согласно свойству степени с целым положительным показателем), что должно выполняться неравенство am<bm.
Используем свойство корней и выведем: amn<bmn
Учитывая положительность значений a и b, перепишем неравенство как amn<bmn. Оно эквивалентно ap<bp.
Таким же образом при m<0 имеем a am>bm, получаем amn>bmn значит, amn>bmn и ap>bp.
Нам осталось привести доказательство последнего свойства. Докажем, что для рациональных чисел p и q, p>q при 0<a<1 ap<aq, а при a>0 будет верно ap>aq.
Рациональные числа p и q можно привести к общему знаменателю и получить дроби m1n и m2n
Здесь m1 и m2 – целые числа, а n – натуральное. Если p>q, то m1>m2 (учитывая правило сравнения дробей). Тогда при 0<a<1 будет верно am1<am2, а при a>1 – неравенство a1m>a2m.
Их можно переписать в следующем виде:
am1n<am2nam1n>am2n
Тогда можно сделать преобразования и получить в итоге:
am1n<am2nam1n>am2n
Подводим итог: при p>q и 0<a<1 верно ap<aq, а при a>0– ap>aq.
Основные свойства степеней с иррациональными показателями
На такую степень можно распространить все описанные выше свойства, которыми обладает степень с рациональными показателями. Это следует из самого ее определения, которое мы давали в одной из предыдущих статей. Сформулируем кратко эти свойства (условия: a>0, b>0, показатели p и q– иррациональные числа):
Определение 4
1. ap·aq=ap+q
2. ap:aq=ap−q
3. (a·b)p=ap·bp
4. (a:b)p=ap:bp
5. (ap)q=ap·q
6. ap<bp верно при любых положительных a и b, если a<b и p – иррациональное число больше 0; если p меньше 0, то ap>bp
7. ap<aq верно, если p и q– иррациональные числа, p<q, 0<a<1; если a>0, то ap>aq.
Таким образом, все степени, показатели которых p и q являются действительными числами, при условии a>0 обладают теми же свойствами.
Источник
Что значит возвести число a в степень n? Это значит, что нужно перемножить это число само на себя n-ное количество раз. Например, число 2, возведенное в степень три, будет выглядеть, как 2*2*2 и равняться 8-ми. И у этих степеней есть свои свойства.
источник: Яндекс
Свойства степеней с натуральным показателем
- Основное свойство степени, или свойство произведения степеней применяется при умножении 2х степеней m и n,которые имеют одинаковое основание a. Данное свойство может быть применимо и к произведению трех и более степеней. То есть, если мы захотим, например, возвести число 5 в степень 2 и умножить это на число 5 в степени 6, то нам нужно будет просто сложить степени, и мы получим 5 в степени 8.
a^m⋅a^n=a^(m+n)
Пример: 5^2⋅5^6=5^8
- Свойство частного степеней применяется при делении степеней m и n с одинаковым основанием а. В результате основание остается таким же, а из показателя степени в числителе вычитается степень в знаменателе. Возьмем, к примеру, число 15 в девятой степени и поделим его на 15 в третей степени. Чтобы не делать долгих вычислений, воспользуемся свойством частного и вычтем из степени 9 степень 3, и мы получим 15 в шестой степени.
a^m:a^n=a^(m−n)
Пример: 15^9:15^3=15^6
- Свойство возведения степени в степень предполагает перемножение степеней, при этом основание остается прежним. Здесь все просто и логично: у нас есть некое число а возведенное в степень 4, и все это нам нужно возвести еще и в третью степень. Пользуясь свойством, мы получаем а в двенадцатой степени.
(a^m)^n=a^(m⋅n)
Пример: (a^4)^3=a^12
Реклама
Не каждый студент может себе позволить за семестр в ВУЗе отдать 100 000 ₽. Но круто, что есть гранты на учебу. Грант-на-вуз.рф – это возможность учиться на желанной специальности. По ссылке каждый получит бонус от 300 ₽ до 100 000 ₽ – грант-на-вуз.рф
- При применении свойства степени произведения, каждый множитель возводится в степень, а полученные результаты перемножаются между собой. Также это свойство можно применять и справа налево.
(a · b)^n = a^n · b^n
Пример: (3 · 4)^5=3^5 · 4^5
- Применяя свойство частного в натуральной степени, и делимое и делитель возводят в степень, а полученный числитель делят на знаменатель.
(a : b)^n = a^n : b^n
Пример: (2 : 7)^6=2^6 : 7^6
- Свойства сравнения степени с нулем:
- если a>0, то при любом натуральном n, a^n>0. Возьмем а равное 6 и n равную натуральному числу 2, следовательно, 6 в степени 2 будет больше нуля;
- при a=0, a^n=0;
- если a<0, и показатель степени будет четным числом 2·m, то a^(2⋅m)>0. Например, а= 3, m=1, делаем из степени четное число (умножаем 2 на 1). Следуя этому свойству, получаем, что 3 в степени 2 больше нуля;
- если a <0, и показатель степени будет нечетным числом 2⋅m−1, то a^(2⋅m−1)>0.
Степень с отрицательным показателем
Если нам нужно возвести число а в отрицательную степень n, то мы делим 1 на число в той же степени, только положительной. Если знаменатель дроби находится в отрицательной степени, то это выражение будет равно произведению числителя на знаменатель в положительной степени. Другими словами, при отрицательной степени выражение переворачивается.
источник: Яндекс
Свойства степеней с целыми показателями
Тут все просто: для степеней с положительными целыми показателями свойства будут такими же ка вышеперечисленные, так как эти показатели будут являться натуральными. Эти же свойства применяются и для отрицательных и равных нулю показателей степеней. Одно важное замечание: основание не должно ровняться 0.
Реклама
Напоминаем про сервис грант-на-вуз.рф. Не упусти свой шанс изучать то, что тебе нравится. Ну или просто сэкономить на учебе. Ты точно получишь от 300 ₽ до 100 000 ₽, перейдя по ссылке грант-на-вуз.рф!
Свойства степеней с рациональными и иррациональными показателями
Они будут такими же, как и свойства для степеней с целыми показателями. Но здесь должно соблюдаться одно правило: основания таких степеней должно быть больше нуля.
Спасибо, что прочитали статью. Не забывайте про подписку на канал, а также рекомендую почитать канал наших друзей:
https://zen.yandex.ru/fgbnuac — последние научные достижения и лучшие образовательные практики.
Хорошего дня и не болейте.
Источник
