Какие свойства у равностороннего треугольника

Равносторонний треугольник, свойства, признаки и формулы.
Равносторонний треугольник – это треугольник, у которого все стороны равны между собой по длине, все углы также равны и составляют 60°.
Равносторонний треугольник (понятие, определение)
Свойства равностороннего треугольника
Признаки равностороннего треугольника
Формулы равностороннего треугольника
Остроугольный треугольник, прямоугольный треугольник, равнобедренный треугольник, равносторонний треугольник, тупоугольный треугольник
Равносторонний треугольник (понятие, определение):
Равносторонний треугольник – это треугольник, у которого все стороны равны между собой по длине, все углы также равны и составляют 60°.
Равносторонний треугольник называется также правильным или равноугольным треугольником.
По определению, каждый правильный (равносторонний) треугольник также является равнобедренным, но не каждый равнобедренный треугольник – правильным (равносторонним). Иными словами, правильный (равносторонний) треугольник является частным случаем равнобедренного треугольника.

Рис. 1. Равносторонний треугольник
АВ = ВС = АС – стороны треугольника, ∠ АВС = ∠ BАC = ∠ BСA = 60° – углы треугольника
Свойства равностороннего треугольника:
1. В равностороннем треугольнике все стороны равны между собой.
2. В равностороннем треугольнике углы равны и составляют 60°.
3. В равностороннем треугольнике каждая медиана, проведенная к каждой стороне, является биссектрисой и высотой, и они равны между собой.
В равностороннем треугольнике биссектриса, проведенная к каждой стороне, является медианой и высотой, и они равны между собой.
В равностороннем треугольнике высота, проведенная к каждой стороне, является биссектрисой и медианой, и они равны между собой.

Рис. 2. Равносторонний треугольник
АK = BF = CD
4. В равностороннем треугольнике высоты, биссектрисы, медианы и серединные перпендикуляры пересекаются в одной точке, которая называется центром равностороннего треугольника. Она же является центром вписанной и описанной окружностей.

Рис. 3. Равносторонний треугольник
R – радиус описанной окружности, r – радиус вписанной окружности
5. В равностороннем треугольнике радиус описанной окружности в два раза больше радиуса вписанной.
6. Точка пересечения высот, биссектрис и медиан правильного треугольника делит каждую из них в отношении 2:1, если считать от вершин.

Рис. 4. Равносторонний треугольник
AO : OK = BO : OА = CO : OD = 2 : 1
Признаки равностороннего треугольника:
– если в треугольнике три угла равны, то он равносторонний;
– если в треугольнике три стороны равны, то он равносторонний.
Формулы равностороннего треугольника:
Пусть a – длина стороны равностороннего треугольника, h – высота (l – биссектриса, m – медиана) равностороннего треугольника, проведенная к каждой стороне, α – угол равностороннего треугольника, α = 60°, R – радиус описанной окружности, r – радиус вписанной окружности (см. Рис. 6).

Рис. 6. Равносторонний треугольник
Формула радиуса вписанной окружности (r):
.
Формула радиуса описанной окружности (R):
,
.
Формулы периметра (Р) равностороннего треугольника:
.
Формулы площади (S) равностороннего треугольника:
.
Формулы высоты (h), медианы (m) и биссектрисы (l) треугольника:
.
Прямоугольный треугольник
Равнобедренный треугольник
Равносторонний треугольник
Примечание: © Фото https://www.pexels.com, https://pixabay.com
карта сайта
Коэффициент востребованности
9 157
Источник
И вот мы снова изучаем треугольники. Это всё больше похоже на заговор…
Не волнуйся: после прочтения этой статьи тайн не останется, ведь ты будешь знать всё о равностороннем треугольнике!
А еще сможешь решить любую задачу на ЕГЭ!
Поехали!
Определение равностороннего треугольника
Равносторонний треугольник — треугольник, у которого все стороны равны.
Какие же особенные свойства присущи равностороннему треугольнику?
Свойства равностороннего треугольника
Свойство 1. В равностороннем треугольнике все углы равны между собой и равны ({{60}^{o }})
Естественно, не правда ли? Три одинаковых угла, в сумме ({{180}^{o }}), значит, каждый по ({{60}^{o }})
Свойство 2. В равностороннем треугольнике точки пересечения высот, биссектрис, медиан и серединных перпендикуляров совпадают – оказываются одной и той же точкой. И эта точка называется центром треугольника (равностороннего!).
Почему так? А посмотрим-ка на равносторонний треугольник:
Он является равнобедренным, какую бы его сторону ни принять за основание – так сказать, со всех сторон равнобедренный.
Значит, любая высота в равностороннем треугольнике является также и биссектрисой, и медианой, и серединным перпендикуляром! В равностороннем треугольнике оказалось не (12) особенных линий, как во всяком обычном треугольнике, а всего три!
Итак, ещё раз:
Центр равностороннего треугольника является центром вписанной и описанной окружности, а также точкой пересечения высот и медиан.
Свойство 3. В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной.
Уже должно быть очевидно, отчего так.
Посмотри на рисунок: точка(O) – центр треугольника. Значит, (OB) – радиус описанной окружности (обозначили его (R)), а (OK) – радиус вписанной окружности (обозначим (r)).
Но ведь точка (O) – ещё и точка пересечения медиан! Вспоминаем, что медианы точкой пересечения делятся в отношении (2:1), считая от вершины.
Поэтому (OB=2cdot OK), то есть (R=2cdot r).
Свойство 4. В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны.
Давай удостоверимся в этом.
Высота равностороннего треугольника
Этот контент доступен после регистрации
Вы также получите доступ к 15 статьям YouClever без ограничений, видеоурокам и другим бесплатным материалам по тарифу “Репетитор”.
(h=frac{asqrt{3}}{2})
Почему?
Рассмотрим (Delta ABK) – он прямоугольный.
(angle A={{60}^{o}}Rightarrow h=acdot sin {{60}^{o}}=frac{asqrt{3}}{2})
Радиус описанной окружности равностороннего треугольника
(R=frac{asqrt{3}}{3})
А это почему?
Мы уже выяснили, что точка (O) – не только центр описанной окружности, но и точка пересечения медиан. Значит, (R=BO=2OK=frac{2}{2}BK=frac{2}{3}h)
Величину (h) мы уже находили. Теперь подставляем:
(R=frac{2}{3}h=frac{2}{3}cdot frac{asqrt{3}}{2}=frac{asqrt{3}}{3})
Радиус вписанной окружности равностороннего треугольника
Чтобы получить полный доступ к этой и другим статьям учебника YouClever, Вам необходимо оплатить курс.
На курсе Вы научитесь решать любые задачи так, чтобы получить
90+ баллов на ЕГЭ
(r=frac{asqrt{3}}{6})
Это уже теперь должно быть совсем ясно:
(R=2cdot rRightarrow r=frac{1}{3}h=frac{1}{3}cdot frac{asqrt{3}}{2}=frac{asqrt{3}}{6})
Ну вот, все основные сведения обсудили. Конечно, можно задавать сотни вопросов про всякие длины всяких отрезков в равностороннем треугольнике.
Но главное, что следует иметь в виду, решая задачки о равностороннем треугольнике, – это то, что все его углы известны – равны ({{60}^{o }}) и все высоты являются и биссектрисами, и медианами, и серединными перпендикулярами.
КОРОТКО О ГЛАВНОМ
Равносторонний треугольник — треугольник, у которого все стороны равны.
(AB=BC=AC=a)
- В равностороннем треугольнике все углы равны между собой и равны ({{60}^{o }}).
- В равностороннем треугольнике каждая медиана совпадает с биссектрисой и высотой, которые проведены из той же вершины;
- Точки пересечения высот, биссектрис, медиан и серединных перпендикуляров равностороннего треугольника совпадают.
- Центры вписанной и описанной окружностей равностороннего треугольника совпадают: точка (O);
- В равностороннем треугольнике радиус описанной окружности в два раза больше, чем радиус вписанной: (R=2cdot r).
В равностороннем треугольнике длины всех элементов «хорошо» выражаются через длину стороны (a):
- Высота=медиана=биссектриса: (h=frac{asqrt{3}}{2});
- Радиус описанной окружности: (R=frac{asqrt{3}}{3});
- Радиус вписанной окружности: (r=frac{asqrt{3}}{6});
- Площадь: (S=frac{{{a}^{2}}sqrt{3}}{4});
- Периметр: (P=3a);
P.S. Последний бесценный совет ????
Ну вот, тема закончена. Если ты читаешь эти строки, значит, ты очень крут.
Почему?
Потому что только 5% людей способны освоить что-то самостоятельно. И если ты дочитал до конца, ты попал в эти 5%!
Теперь самое главное.
Ты разобрался с теорией по этой теме. И, повторюсь, это… это просто супер! Ты уже лучше, чем абсолютное большинство твоих сверстников.
Проблема в том, что этого может не хватить…
Для чего?
Для успешной сдачи ОГЭ или ЕГЭ, для поступления в 10 класс или в институт на бюджет и, самое главное, для жизни.
Я не буду тебя ни в чем убеждать, просто скажу одну вещь…
Люди, получившие хорошее образование, зарабатывают намного больше, чем те, кто его не получил. Это статистика.
Но и это не главное.
Главное то, что они более счастливы (есть такие исследования). Возможно, потому, что перед ними открывается гораздо больше возможностей и жизнь становится ярче? Не знаю…
Но думай сам…
Что нужно, чтобы быть наверняка лучше других на ОГЭ или ЕГЭ и быть в конечном итоге… более счастливым?
Набить руку, решая задачи.
На экзамене у тебя не будут спрашивать теорию.
Тебе нужно будет решать задачи на время. И, если ты не решал их (много!), ты обязательно где-нибудь глупо ошибешься или просто не успеешь. Это как в спорте: нужно много раз повторить, чтобы выиграть наверняка.
Найди где хочешь сборник, обязательно с решениями, подробным разбором и решай, решай, решай!
Можешь воспользоваться нашим сборником задач с подробным разбором, и мы их всячески рекомендуем, потому что они разбиты по темам, по типам и даже собраны в целую программу подготовки.
Если решишь набить руку с помощью наших задач, зайди на сайт 100gia и приобрети одну из программ.
А еще можешь зарегистрироваться и получить доступ к огромному количеству бесплатных материалов, видеоуроков, тестов.
После регистрации ты сможешь:
- проверить свою готовность к каждому типу задач на ЕГЭ (пройдя тест);
- подтянуть слабые места с помощью видеоуроков, вебинаров;
- понять тему с помощью статей учебника YouClever;
- набить руку, решая задачи и получая проверку и решения;
- сдать пробный ЕГЭ и получить сразу оценку и разбор ошибок.
Бонус: информатика и физика.
И в заключение…
Если наши задачи тебе не нравятся, найди другие. Только не останавливайся на теории.
“Понял” и “Умею решать” – это совершенно разные навыки. Тебе нужны оба.
Найди задачи и решай!
Поговорим о тебе?
Равносторонний треугольник, как ты заметил, находится в очень удобной позиции!
С одной стороны, для него выполняются все свойства равнобедренного треугольника. С другой стороны, он очень интересен как правильная фигура (а интересна она связью с окружностями!).
Но сейчас не об этом… Расскажи нам, как тебе статья? Понравилась?
Напиши в комментариях!
А еще пиши, если есть вопросы. Мы обязательно тебе ответим.
Удачи!
Источник
В этой статье описаны все свойства, правила и определения равностороннего треугольника.
Математика — любимый предмет многих школьников, особенно тех, у которых получается решать задачи. Геометрия — это также интересная наука, но не все дети могут понять новый материал на уроке. Поэтому им приходится дорабатывать и доучивать дома. Давайте повторим правила равностороннего треугольника. Читайте ниже.
Все правила равностороннего треугольника: свойства
В самом слове «равносторонний» скрывается определение этой фигуры.
Определение равностороннего треугольника: Это треугольник, у которого все стороны равны друг другу.
Из-за того, что равносторонний треугольник – это в некотором роде равнобедренный треугольник, у него появляются признаки последнего. Например, в этих треугольниках биссектриса угла является еще медианой и высотой.
Вспомним: Биссектриса — луч, делящий угол пополам, медиана – луч, выпущенный из вершины, делящий противолежащую сторону пополам, а высота — это перпендикуляр, исходящий из вершины.
Вторым признаком равностороннего треугольника является то, что все его углы равны между собой и каждый из них имеет градусную меру в 60 градусов. Вывод об этом можно сделать из общего правила о сумме углов треугольника, равной 180 градусам. Следовательно, 180:3=60.
Следующее свойство: центром равностороннего треугольника, а также вписанной в него и описанной около него окружностей является точка пересечения всех его медиан (биссектрис).
Четвертое свойство: радиус описанной около равностороннего треугольника окружности превышает в два раза радиус вписанной окружности в эту фигуру. Убедиться в этом можно, посмотрев на чертеж. ОС является радиусом описанной около треугольника окружности, а ОВ1 — радиусом вписанной. Точка О — место пересечения медиан, значит, разделяет ее как 2:1. Из этого делаем вывод, что ОС = 2ОВ1.
Пятым свойством является то, что в этой геометрической фигуре легко посчитать составляющие элементы, если в условии указана длина одной стороны. При этом чаще всего используется теорема Пифагора.
Шестое свойство: площадь такого треугольника вычисляется по формуле S=(а^2*3) /4.
Седьмое свойство: радиусы окружности, описанной около треугольника, и окружности, вписанной в треугольник, соответственно равны
R = (a3) /3 и r = (a3) /6.
Рассмотрим примеры задач:
Пример 1:
Задача: Радиус окружности, вписанной в равносторонний треугольник равен 7 см. Найдите высоту треугольника.
Решение:
- Радиус вписанной окружности связан с последней формулой, следовательно, OM = (BC3) /6.
- BC = (6 * OM) /3 = (6*7) /3 = 143.
- AM = (BC3) /2; AM = (143*3) /2 = 21.
- Ответ: 21 см.
Эту задачу можно решить по-другому:
- Исходя из четвертого свойства, можно сделать вывод, что ОМ = 1/2 АМ.
- Следовательно, если ОМ равно 7, то АО равно 14, а АМ равно 21.
Пример 2:
Задача: Радиус описанной около треугольника окружности равен 8. Найдите высоту треугольника.
Решение:
- Пусть АВС – равносторонний треугольник.
- Как и в предыдущем примере, можно идти двумя путями: более простым – АО = 8 => ОМ =4. Тогда АМ = 12.
- И более длинным – чтобы найти АМ через формулу. АМ = (АС3) /2 = (83*3) /2 = 12.
- Ответ: 12.
Как видите, зная свойства и определение равностороннего треугольника, вы сможете решить любую задачу по геометрии по этой теме.
Видео: Геометрия Равносторонний треугольник
Источник
Общие сведения
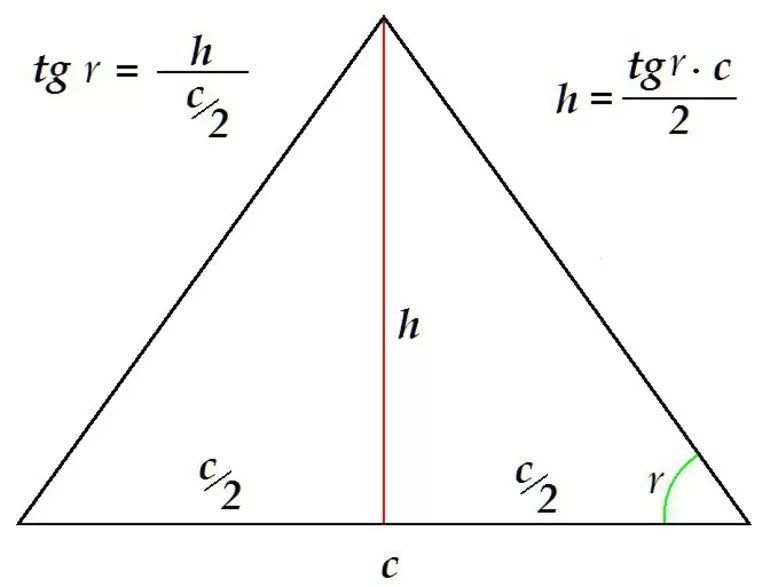
Любое пространство можно описать размерностью. В трёхмерном измерении плоская геометрическая фигура, состоящая из трёх отрезков и такого же количества точек, в которых они соединяются, называется треугольником. Отрезки называют сторонами или боковыми гранями, площадь, ограниченная ими — внутренней, а точки — вершинами. Фигура имеет 3 угла и является невырожденной.
Строгого требования к обозначениям элементов многоугольника нет. Но традиционно вершины подписывают заглавными буквами латинского алфавита A, B, C, а противолежащие им стороны — аналогичными строчными знаками. В качестве обозначений для углов используют греческие символы: α, β, γ. Например, если имеется треугольник ABC, у него будут углы A, B, C и стороны a, b, c. Боковые грани могут подписываться и как отрезки, тогда в их имени учитываются ограничивающие точки. Например, AB, BC, CA.
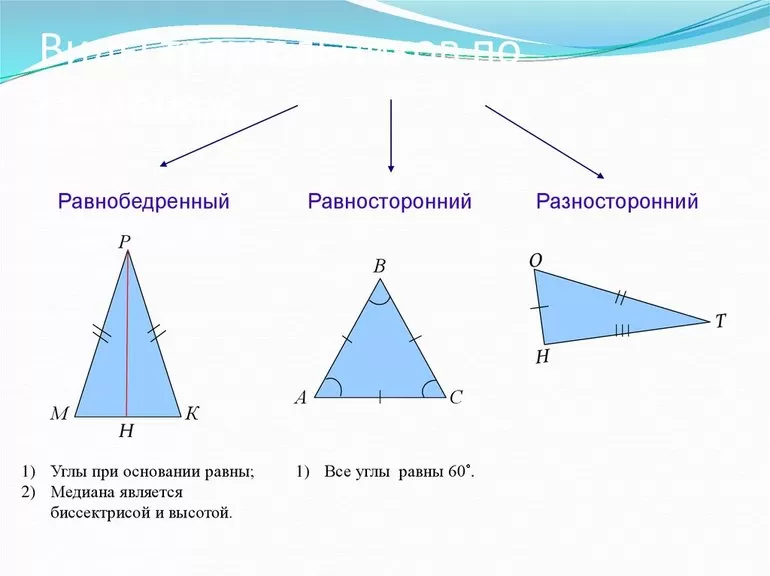
В зависимости от соотношения размеров сторон, все треугольники разделяют на 3 вида. Они бывают:
- Равнобедренными — многоугольники, у которых одна сторона не равна двум другим. Эта грань называется основанием. Углы при этой стороне равны.
- Разносторонние (неправильные) — длины всех граней разные.
- Равносторонние — треугольники, имеющие одинаковые стороны. Часто эти фигуры называют правильными. По сути, они являются частным случаем равнобедренного многоугольника.
Существуют правила, позволяющие утверждать о равенстве или подобии двух и более треугольников. Они считаются идентичными, то есть их параметры полностью совпадают, если 2 стороны и угол равны или все грани имеют одинаковую длину. А также фигуры будут одинаковыми, когда у них совпадают 2 стороны и угол, располагающийся напротив большего отрезка.
Признаки подобия помогают определить вид треугольника при сравнении с известным. Если 2 любых угла равны в обеих фигурах, они считаются похожими. Когда же 2 стороны многоугольника пропорциональны двум отрезкам другого, причём углы, заключённые между этими гранями, равны, такие фигуры подобны.
Особые линии и точки
Медиана, высота и биссектриса — 3 замечательные линии любого треугольника. Представляют они собой внутренние отрезки, построенные из углов на противоположные стороны. Линия, соединяющая вершину с серединой противоположной грани, называется медианой. Луч, разделяющий угол на 2 равные части — это биссектриса, а перпендикуляр, построенный к стороне — высота.
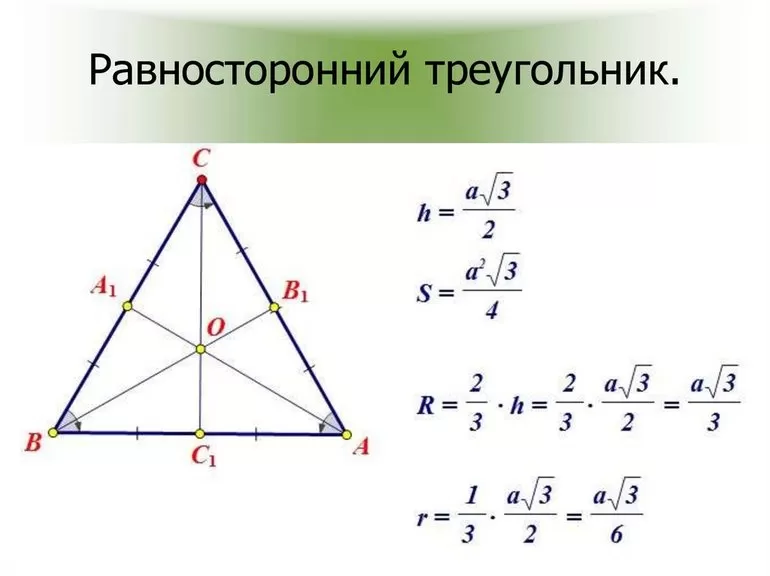
В любом правильном треугольнике можно начертить 3 отрезка. Если отложить медиану, а потом биссектрису и высоту, можно заметить, что эти линии совпадут. Эта особенность и есть замечательным свойством равностороннего многоугольника, то есть если в любой другой трёхугольной фигуре можно построить 12 особых линий, то в рассматриваемом только 3.
Доказать это утверждение можно следующим образом: пусть имеется треугольник АВС, в котором проведена высота ВH. Далее, рассуждения нужно построить так:

- Отрезок BH перпендикулярен прямой AC по построению.
- Точка H разделяет отрезок AC на AD и CD. Если это утверждение будет верным, это означает, что построенная высота BH будет медианой треугольника.
- Отрезок BH создаёт в многоугольнике 2 угла — ∠ABH и ∠CBH. При верности этого утверждения можно утверждать, что отрезок BH является биссектрисой.
Если создать зеркальное отражение треугольнику и совместить его с оригинальным, все углы попарно совместятся. Совпадут и стороны. Так как ВH — высота, она перпендикуляр. Значит, в точке H отрезок образует прямой угол с боковой гранью AC. Отсюда следует, что образованные треугольники AHB и CBH прямоугольные.
Они являются равными по общей гипотенузе и острому углу. Это следует из того, что правильный многоугольник — частный случай равнобедренного. Так как треугольники совпадают, у них одинаковые углы ABH и CBH. Причём они смежные, поэтому BH — биссектриса. В то же время точка H делит AC на 2 равных отрезка, значит, BH — медиана.
Точка, в которой пересекаются отрезки, будет центром тяжести фигуры. Её особенность в том, что она разделяет эту линию на 2 части в отношении 2 к 1, если считать от угла. Кроме этого, из-за равенства медианы и биссектрисы эта точка будет и ортоцентром.
Основные формулы
Для каждого треугольника существует набор формул, с помощью которых можно определить его элементы. Чаще всего приходится выяснять длины сторон, площадь, высоты и периметр. При этом если известны боковые грани, можно найти практически любые остальные параметры.
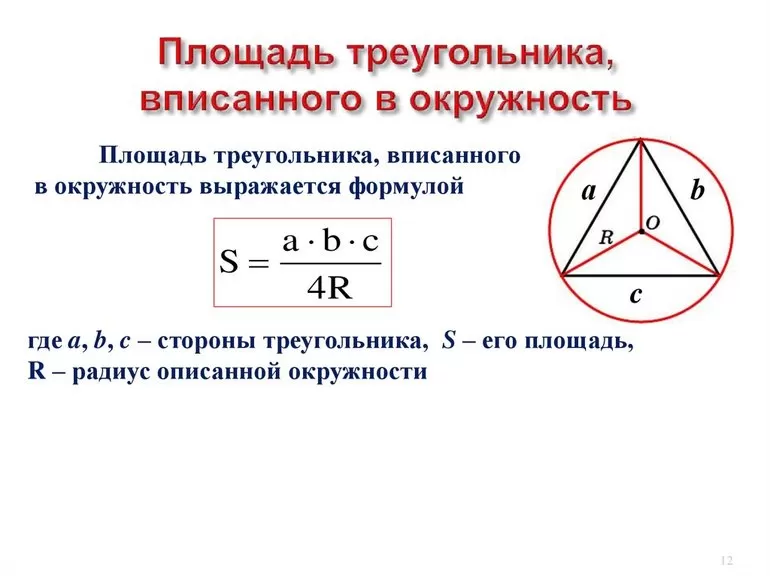
Вокруг правильной фигуры можно описать круг, причём окружность можно и вписать в середину. Что интересно, их центры совпадут между собой и с местом пересечения высот. В этом случае радиус внешнего круга равняется R = (a * √3) / 3 = a / 2 * sin (a), а внутреннего: r = (a * √3) / 6 = R / 2. Чтобы найти высоту, зная радиус, используют выражение: h = (3 *R) / 2. Кроме этой формулы, довольно часто применяют равенство, связывающее сторону и перпендикуляр: h = (a * √3) / 2.
Доказательство верности формулы для нахождения радиуса вписанной окружности можно построить исходя из выражения, справедливого к равнобедренной фигуре: r = b / 2 √((2 a — b) / (2 a + b)). Так как стороны равны, то a = b. Получается, что r = a / 2 √(2a — a) / (2a + a) = (a / 2) * √(1 / 3) = a / (2 * √3) = (a √3) / 6.
Чтобы определить длину стороны, нужно знать высоту и теорему Пифагора. Согласно ей, квадрат гипотенузы находится как сумма квадратов высоты и длины разделённого основания. Применяя теорему к правильной фигуре, можно записать: AB2 = h2 + (AB / 2)2. Это равенство решают следующим образом: AB2 = h2 + AB2 / 22. Выражение можно преобразовать в вид: (3a2 / 4) = h 2 → a 2 = (4 * h2) / 3 → a 2 = √((4 * h2) / 3) → a = (2 * h) / √3.
Из других существующих формул можно перечислить те, что чаще всего применяют при решении примеров:
- Площадь. Находят из выражения: S = (a 2 * √3) / 4. Вывести эту формулу довольно просто. Если взять за основу, что равенство для площади верно, то исходя из свойств фигуры можно записать: S = ½ * a2 * sin 60 = ½ * a2 * √3 / 2 = (√3 / 4) * a2. Что и следовало доказать.
- Периметр. Чтобы его определить, нужно сложить длины всех сторон, но так как в правильной фигуре они равны, можно воспользоваться формулой: P = 3 * a.
Существуют ещё 2 значимые теоремы: косинусов и синусов. Согласно первой, квадрат стороны фигуры будет ранятся удвоенному произведению двух оставшихся отрезков и косинусу угла между ними, отнятому из суммы квадратов: a2 = b2 + c2 — 2 * b * c * cos (a). Согласно же второй, длины отрезков пропорциональны синусам углов, лежащих напротив: a / sin (a) = b / sin (b) = c / sinс.
Решение задач
Чтобы уметь решать различные задания, связанные с треугольником, нужно помнить всего несколько формул. Но понадобится знать, что углы в фигуре равны друг другу и составляют 60 градусов. Часто придётся применять и теорему Пифагора. Вот некоторые из типовых заданий, используемые при обучении школьников в седьмом классе:
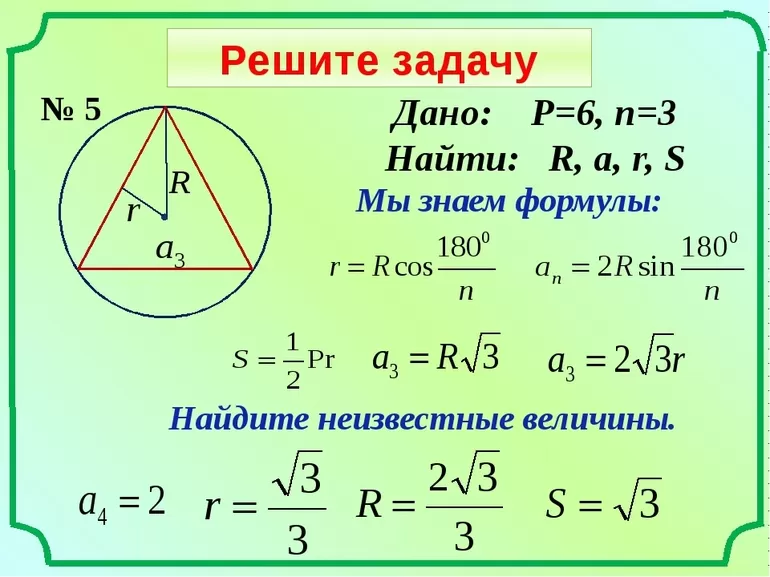
- Какой будет радиус вписанной в правильный треугольник окружности, если его высота равняется 9 см. Зная свойство фигуры, решить задачу можно за пару секунд. Так как радиус равен 1/3 высоты, ответом на задачу будет: r = h / 3 = 9 / 3 = 3 см.
- Сторона равностороннего треугольника равняется корню из трёх. Определить диаметр описанной окружности. Известно, что отношение синуса к противолежащему углу составляет 2R. Следовательно: R = a / 2 * sin (a) = √3 * 2 / 2 * √3 = 1.
- Вокруг треугольной фигуры со стороной 8 √3 описан круг. Узнать его радиус. Эта задача в 2 действия. Используя формулу для нахождения вписанного радиуса и определение r = R / 2 можно записать: R = 2 * a * √3 / 6 = 2 * 8 * √3 * √3 / 6 = 2 * 4 = 8.
- Пусть имеется квадрат, вокруг которого описана окружность. В ней так же располагается правильный треугольник. Периметр треугольной фигуры равен 9 √ 6. Нужно вычислить сумму всех сторон квадрата. На первом шаге необходимо определить длину боковой грани треугольника. Найти её можно по формуле: a = 3 √6. Теперь возможно рассчитать радиус описанной окружности: a = R * √3. Выполнив подстановку, найти ответ несложно: R = 3 √6 / √3 = 3 * √2. На третьем шаге можно выяснить, чему равняется сторона четырёхугольника. В этом поможет равенство: 3 √2 = (n √2) / 2. Отсюда n = 6. Значит, периметр квадрата равняется: P = 4 * 6 = 24.
Проверить правильность решения, возможно, используя онлайн-калькуляторы. Это сервисы, которые предлагают бесплатно вычислить элементы правильной фигуры. При этом от пользователя требуется лишь внести в специальную форму исходные данные и нажать кнопку «Рассчитать».
Следует отметить, что выучить наизусть все формулы сложно, поэтому обычно используют логическое мышление и теоремы синусов-косинусов. Учитывая, что любой угол в равностороннем треугольнике равен 60 градусов практически любую формулу вывести можно самостоятельно.
Источник
