Какие свойства у равнобедренной трапеции
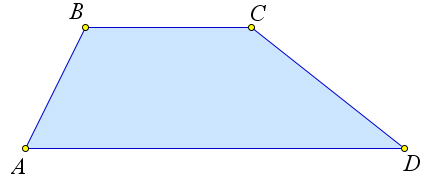
Определение.
Равнобедренная трапеция — это трапеция у котрой боковые стороны равны.
На этой странице представленны формулы характерные равнобедренной трапеции. Не забывайте, что для равнобедренной трапеции выполняются все формулы и свойства трапеции.
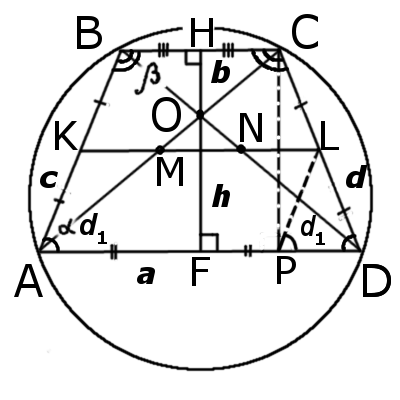 |
| Рис.1 |
Признаки равнобедренной трапеции
Трапеция будет равнобедренной если выполняется одно из этих условий:
1. Углы при основе равны:
∠ABC = ∠BCD и ∠BAD = ∠ADC
2. Диагонали равны:
AC = BD
3. Одинаковые углы между диагоналями и основаниями:
∠ABD = ∠ACD, ∠DBC = ∠ACB, ∠CAD = ∠ADB, ∠BAC = ∠BDC
4. Сумма противоположных углов равна 180°:
∠ABC + ∠ADC = 180° и ∠BAD + ∠BCD = 180°
5. Вокруг трапеции можно описати окружность
Основные свойства равнобедренной трапеции
1. Сумма углов прилегающих к боковой стороне равнобедренной трапеции равна 180°:
∠ABC + ∠BAD = 180° и ∠ADC + ∠BCD = 180°
2. Если в равнобедренную трапецию можно вписать окружность, то боковая сторона равна средней лини трапеции:
AB = CD = m
3. Вокруг равнобедренной трапеции можно описать окружность
4. Если диагонали взаимно перпендикулярны, то высота равна полусумме оснований (средней лини):
h = m
5. Если диагонали взаимно перпендикулярны, то площадь трапеции равна квадрату высоты:
SABCD = h2
6. Если в равнобедренную трапецию можно вписать окружность, то квадрат высоты равен произведению основ трапеции:
h2 = BC · AD
7. Сумма квадратов диагоналей равна сумме квадратов боковых сторон плюс удвоенному произведению основ трапеции:
AC2 + BD2 = AB2 + CD2 + 2BC · AD
8. Прямая, проходящая через середины оснований, перпендикулярна основаниям и является осью симметрии трапеции:
HF ┴ BC, HF ┴ AD
9. Высота (CP), опущенная из вершины (C) на большее основание (AD), делит его на большой отрезок (AP), который равен полусумме оснований и меньший (PD) – равен полуразности оснований:
Стороны равнобедренной трапеции
Формулы длин сторон равнобедренной трапеции:
1. Формулы длины сторон через другие стороны, высоту и угол:
a = b + 2h ctg α = b + 2c cos α
b = a – 2h ctg α = a – 2c cos α
| c = | h | = | a – b |
| sin α | 2 cos α |
2. Формула длины сторон трапеции через диагонали и другие стороны:
| a = | d12 – c2 | b = | d12 – c2 | c = √d12 – ab |
| b | a |
3. Формулы длины основ через площадь, высоту и другую основу:
| a = | 2S | – b b = | 2S | – a |
| h | h |
4. Формулы длины боковой стороны через площадь, среднюю линию и угол при основе:
5. Формулы длины боковой стороны через площадь, основания и угол при основе:
Средняя линия равнобедренной трапеции
Формулы длины средней линии равнобедренной трапеции:
1. Формула определения длины средней линии через основания, высоту и угол при основании:
m = a – h ctg α = b + h ctg α = a – √c2 – h2 = b + √c2 – h2
2. Формула средней линии трапеции через площадь и сторону:
Высота равнобедренной трапеции
Формулы определения длины высоты равнобедренной трапеции:
1. Формула высоты через стороны:
2. Формула высоты через стороны и угол прилегающий к основе:
| h = | a – b | tg β | = c sin β |
| 2 |
Диагонали равнобедренной трапеции
Диагонали равнобедренной трапеции равны:
d1 = d2
Формулы длины диагоналей равнобедренной трапеции:
1. Формула длины диагонали через стороны:
d1 = √с2 + ab
2. Формулы длины диагонали по теореме косинусов:
d1 = √a2 + c2 – 2ac cos α
d1 = √b2 + c2 – 2bc cos β
3. Формула длины диагонали через высоту и среднюю линию:
d1 = √h2 + m2
4. Формула длины диагонали через высоту и основания:
Площадь равнобедренной трапеции
Формулы площади равнобедренной трапеции:
1. Формула площади через стороны:
| S = | a + b | √4c2 – (a – b)2 |
| 4 |
2. Формула площади через стороны и угол:
S = (b + c cos α) c sin α = (a – c cos α) c sin α
3. Формула площади через радиус вписанной окружности и угол между основой и боковой стороной:
| S = | 4 r 2 | = | 4 r 2 |
| sin α | sin β |
4. Формула площади через основания и угол между основой и боковой стороной:
5. Формула площади ранобедренной трапеции в которую можно вписать окружность:
S = (a + b) · r = √ab·c = √ab·m
6. Формула площади через диагонали и угол между ними:
| S = | d12 | · sin γ | = | d12 | · sin δ |
| 2 | 2 |
7. Формула площади через среднюю линию, боковую сторону и угол при основании:
S = mc sin α = mc sin β
8. Формула площади через основания и высоту:
Окружность описанная вокруг трапеции
Окружность можно описать только вокруг равнобедренной трапеции!!!
Формула определения радиуса описанной вокруг трапеции окружности:
1. Формула радиуса через стороны и диагональ:
| R = | a·c·d1 |
| 4√p(p – a)(p – c)(p – d1) |
где
a – большее основание
Источник
Равнобедренная трапеция, её ещё называют равнобокой, имеет равные боковые стороны. Кроме этого, у нее в арсенале есть еще множество интересных и полезных свойств, которые можно с легкостью применять на практике или при решении математических задач.
Определение, признаки и элементы трапеции
Трапецией в геометрии принято называть любой четырехугольник, у которого есть две параллельные друг другу стороны, при том что продолжения других двух сторон пересекаются.
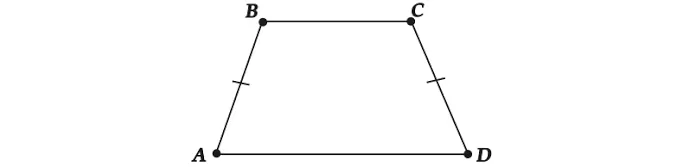
Определение же равнобедренной трапеции идет от того, что у нее боковые стороны эквиваленты по длине.
Свойства равнобедренной трапеции
Существует всего несколько основных свойств, присущих именно данной фигуре. Сейчас мы рассмотрим каждое из них:
- Прямая, которая проходит через середину оснований такой трапеции, является ее осью симметрии, а также она перпендикулярна ее основаниям.
- Углы при основаниях трапеции равны.
- У равнобедренной трапеции также равны и длины диагоналей. Если диагонали перпендикулярны, тогда высота трапеции будет равна сумме основания, деленной на 2.
- Диагональ разбивает фигуру на 2 треугольника.
- Биссектрисы углов, принадлежащих одной и той же боковой стороне, всегда перпендикулярны друг другу.
- Если мы опустим высоту на большее из оснований трапеции, то получим в итоге 2 отрезка АЕ и ЕВ:
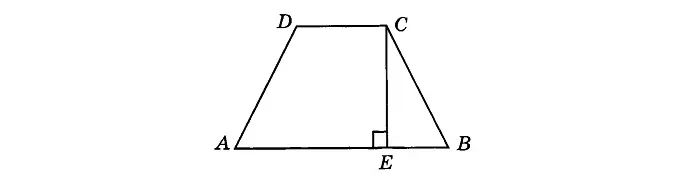
Первый отрезок АЕ будет равен сумме оснований, деленной на 2, а второй отрезок ЕВ – разности, разделенной на 2:
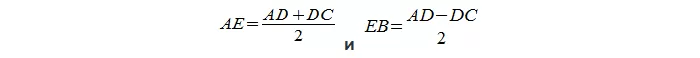
Периметр равнобедренной трапеции
Эту величину найти очень просто. Простейшей формулой будет сложение всех ее сторон. Однако иногда составители задач не дают нам информацию обо всех из сторон.
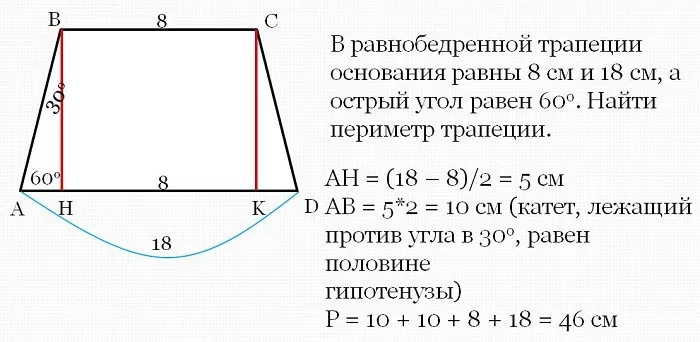
В таком случае нам следует в первую очередь найти все стороны фигуры, а затем уже приступать к их сложению.
Как найти стороны трапеции?
Существует множество различных способов решения данной задачи, однако мы предложим только некоторые из них.
В первую очередь можно найти стороны с помощью средней линии:
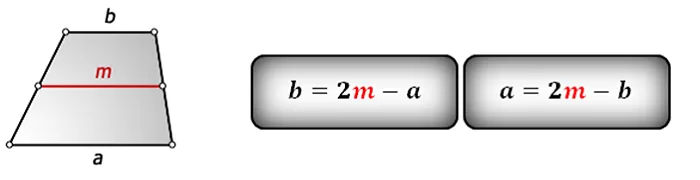
Есть альтернатива, если вам известны высота и угол при большем основании:
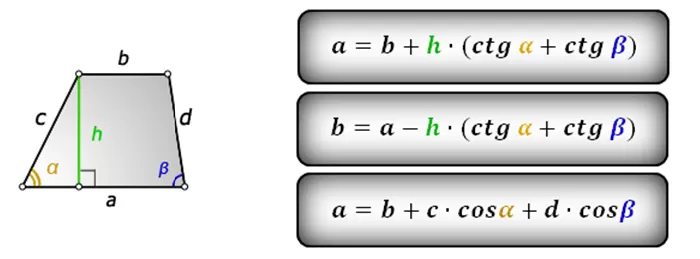
Средняя линия
Средней линией в трапеции называется параллельный основаниям отрезок, который делит боковые стороны фигуры на равные части.
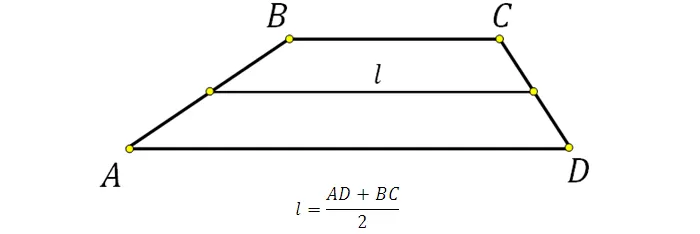
У нее есть множество интересных свойств и теорем с нетрудным доказательством, таких как, например, решение задач на подобие, однако мы на них останавливаться не будем.
Высота трапеции
Высотой трапеции называется самый короткий по длине отрезок, который продолжается ровно от одного основания до другого. Он выполняет своеобразную вспомогательную роль в задачах вплоть до 10 класса с неизвестными сторонами и в тех задачах, где нужно дополнить фигуру до прямоугольника, например.
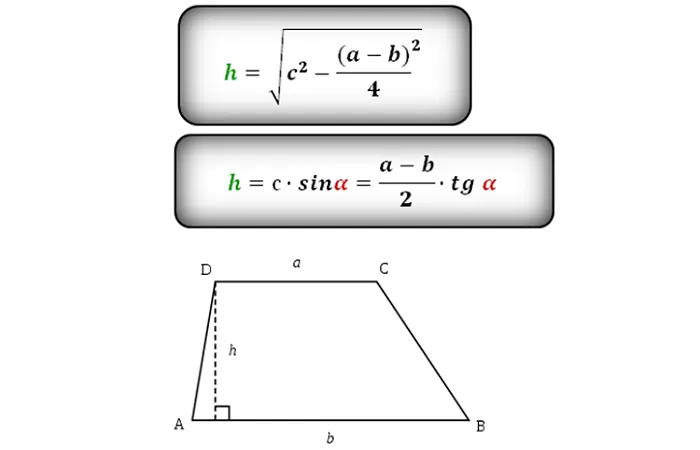
Для нахождения длины этого отрезка нам необходимо знать оба основания (a и b), а также боковую сторону c. Также полезно было бы знать угол при большем основании α. Формулы здесь довольно простые и не нуждаются в доказательстве.
Диагональ трапеции
Эта линия просто идет от одного угла трапеции к другому, причем эти углы противоположны. В равнобедренной трапеции довольно приятным фактом является то, что диагонали в ней равны друг другу.
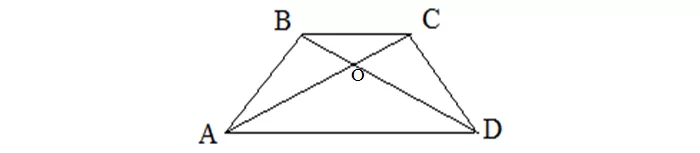
А каким образом можно найти длину диагонали? Есть один очень простой способ. Мы можем сделать это, зная все три величины: боковую сторону и каждое из оснований:
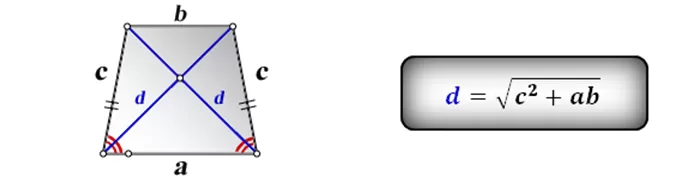
Площадь равнобедренной трапеции
Самой простой формулой является полусумма оснований, умноженная на высоту. Она подходит к любым трапециям.

Для второй формулы нужно знать все стороны трапеции. Это по сути усложненная версия первой, но подойдет она в том случае, если вы не знаете высоту.
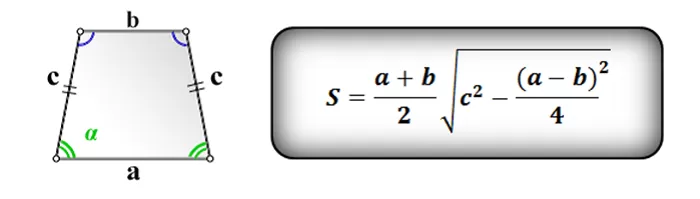
Это самые базовые формулы, поэтому очень часто используются в различных задачах.
Вписанная и описанные окружности
Интересно, что вписать в трапецию окружность можно только при определенном условии. И это условие выполняется, если мы попарно сложим противоположные стороны нашего четырехугольника, и эти суммы окажутся равны.
Найти радиус этой окружности не составит труда. Нужно просто разделить высоту пополам.
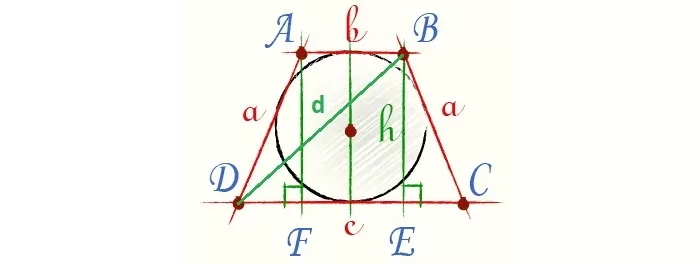
А вот с описанной окружностью все не так гладко. Есть различные полезные формулы. Например, если диагональ составляет с основанием прямой угол, то диаметр описанной окружности будет равен противоположному основанию трапеции.
Теперь разберемся с формулой нахождения радиуса. К слову, она здесь не очень простая. Сначала найдем p — полупериметр ∆DBC, а затем просто применим его в следующей формуле:
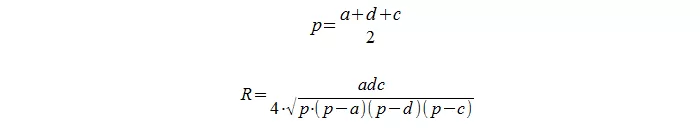
Математика бесспорно является матерью всех современных наук. Она по праву занимает свой престол и управляет абсолютно всеми мировыми законами.
Одной из наиболее интересных подразделений математики принято считать именно геометрию. Ее фигуры также подчиняются математическим правилам и формулам, поэтому она необходима при различных сложных расчетах.
Источник
[{Large{text{Произвольная трапеция}}}]
Определения
Трапеция – это выпуклый четырехугольник, у которого две стороны параллельны, а две другие стороны не параллельны.
Параллельные стороны трапеции называются её основаниями, а две другие стороны – боковыми сторонами.
Высота трапеции – это перпендикуляр, опущенный из любой точки одного основания к другому основанию.
Теоремы: свойства трапеции
1) Сумма углов при боковой стороне равна (180^circ).
2) Диагонали делят трапецию на четыре треугольника, два из которых подобны, а два другие – равновелики.
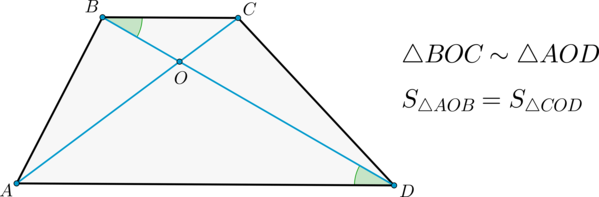
Доказательство
1) Т.к. (ADparallel BC), то углы (angle BAD) и (angle ABC) – односторонние при этих прямых и секущей (AB), следовательно, (angle
BAD
+angle ABC=180^circ).
2) Т.к. (ADparallel BC) и (BD) – секущая, то (angle DBC=angle
BDA) как накрест лежащие.
Также (angle BOC=angle AOD) как вертикальные.
Следовательно, по двум углам (triangle BOC sim triangle AOD).
Докажем, что (S_{triangle AOB}=S_{triangle COD}). Пусть (h) – высота трапеции. Тогда (S_{triangle ABD}=frac12cdot hcdot
AD=S_{triangle ACD}). Тогда: [S_{triangle AOB}=S_{triangle ABD}-S_{triangle AOD}=S_{triangle ACD}-S_{triangle AOD}=S_{triangle
COD}]
Определение
Средняя линия трапеции – отрезок, соединяющий середины боковых сторон.
Теорема
Средняя линия трапеции параллельна основаниям и равна их полусумме.
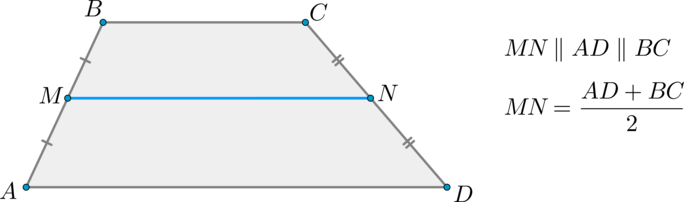
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем параллельность.
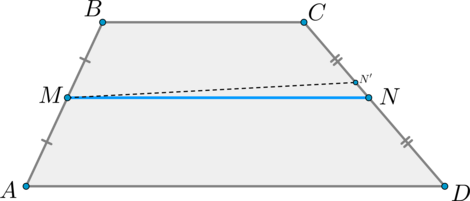
Проведем через точку (M) прямую (MN’parallel AD) ((N’in CD)). Тогда по теореме Фалеса (т.к. (MN’parallel ADparallel BC, AM=MB)) точка (N’) — середина отрезка (CD). Значит, точки (N) и (N’) совпадут.
2) Докажем формулу.
Проведем (BB’perp AD, CC’perp AD). Пусть (BB’cap MN=M’, CC’cap
MN=N’).
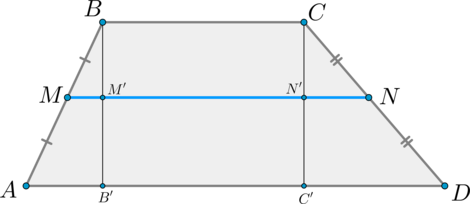
Тогда по теореме Фалеса (M’) и (N’) — середины отрезков (BB’) и (CC’) соответственно. Значит, (MM’) – средняя линия (triangle
ABB’), (NN’) — средняя линия (triangle DCC’). Поэтому: [MM’=dfrac12 AB’, quad NN’=dfrac12 DC’]
Т.к. (MNparallel ADparallel BC) и (BB’, CC’perp AD), то (B’M’N’C’) и (BM’N’C) – прямоугольники. По теореме Фалеса из (MNparallel AD) и (AM=MB) следует, что (B’M’=M’B). Значит, (B’M’N’C’) и (BM’N’C) – равные прямоугольники, следовательно, (M’N’=B’C’=BC).
Таким образом:
[MN=MM’+M’N’+N’N=dfrac12 AB’+B’C’+dfrac12 C’D=] [=dfrac12 left(AB’+B’C’+BC+C’Dright)=dfrac12left(AD+BCright)]
Теорема: свойство произвольной трапеции
Середины оснований, точка пересечения диагоналей трапеции и точка пересечения продолжений боковых сторон лежат на одной прямой.
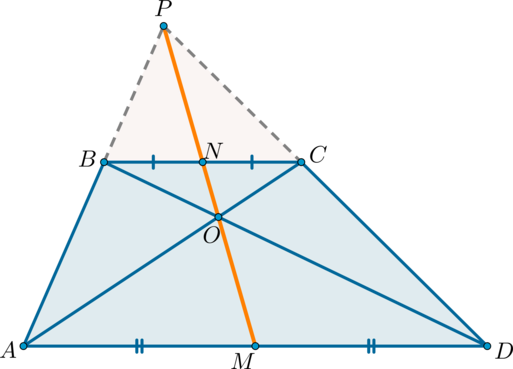
Доказательство*
С доказательством рекомендуется ознакомиться после изучения темы “Подобие треугольников”.
1) Докажем, что точки (P), (N) и (M) лежат на одной прямой.
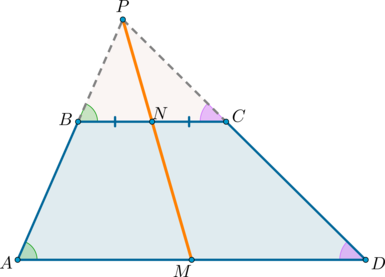
Проведем прямую (PN) ((P) – точка пересечения продолжений боковых сторон, (N) – середина (BC)). Пусть она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
Рассмотрим (triangle BPN) и (triangle APM). Они подобны по двум углам ((angle APM) – общий, (angle PAM=angle PBN) как соответственные при (ADparallel BC) и (AB) секущей). Значит: [dfrac{BN}{AM}=dfrac{PN}{PM}]
Рассмотрим (triangle CPN) и (triangle DPM). Они подобны по двум углам ((angle DPM) – общий, (angle PDM=angle PCN) как соответственные при (ADparallel BC) и (CD) секущей). Значит: [dfrac{CN}{DM}=dfrac{PN}{PM}]
Отсюда (dfrac{BN}{AM}=dfrac{CN}{DM}). Но (BN=NC), следовательно, (AM=DM).
2) Докажем, что точки (N, O, M) лежат на одной прямой.
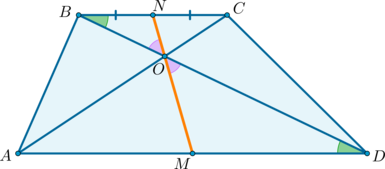
Пусть (N) – середина (BC), (O) – точка пересечения диагоналей. Проведем прямую (NO), она пересечет сторону (AD) в точке (M). Докажем, что (M) – середина (AD).
(triangle BNOsim triangle DMO) по двум углам ((angle OBN=angle
ODM) как накрест лежащие при (BCparallel AD) и (BD) секущей; (angle BON=angle DOM) как вертикальные). Значит: [dfrac{BN}{MD}=dfrac{ON}{OM}]
Аналогично (triangle CONsim triangle AOM). Значит: [dfrac{CN}{MA}=dfrac{ON}{OM}]
Отсюда (dfrac{BN}{MD}=dfrac{CN}{MA}). Но (BN=CN), следовательно, (AM=MD).
[{Large{text{Равнобедренная трапеция}}}]
Определения
Трапеция называется прямоугольной, если один из ее углов – прямой.
Трапеция называется равнобедренной, если ее боковые стороны равны.
Теоремы: свойства равнобедренной трапеции
1) У равнобедренной трапеции углы при основании равны.
2) Диагонали равнобедренной трапеции равны.
3) Два треугольника, образованные диагоналями и основанием, являются равнобедренными.
Доказательство
1) Рассмотрим равнобедренную трапецию (ABCD).
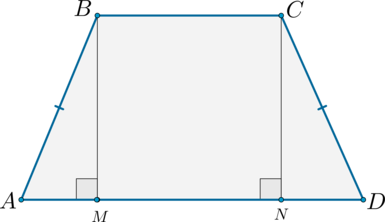
Из вершин (B) и (C) опустим на сторону (AD) перпендикуляры (BM) и (CN) соответственно. Так как (BMperp AD) и (CNperp AD), то (BMparallel CN); (ADparallel BC), тогда (MBCN) – параллелограмм, следовательно, (BM = CN).
Рассмотрим прямоугольные треугольники (ABM) и (CDN). Так как у них равны гипотенузы и катет (BM) равен катету (CN), то эти треугольники равны, следовательно, (angle DAB = angle CDA).
2) 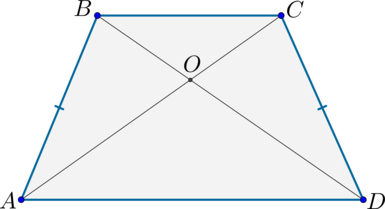
Т.к. (AB=CD, angle A=angle D, AD) – общая, то по первому признаку (triangle ABD=triangle ACD). Следовательно, (AC=BD).
3) Т.к. (triangle ABD=triangle ACD), то (angle BDA=angle CAD). Следовательно, треугольник (triangle AOD) – равнобедренный. Аналогично доказывается, что и (triangle BOC) – равнобедренный.
Теоремы: признаки равнобедренной трапеции
1) Если у трапеции углы при основании равны, то она равнобедренная.
2) Если у трапеции диагонали равны, то она равнобедренная.
Доказательство
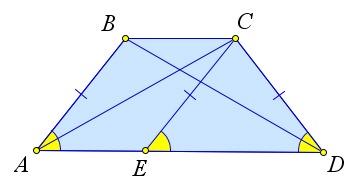
Рассмотрим трапецию (ABCD), такую что (angle A = angle D).
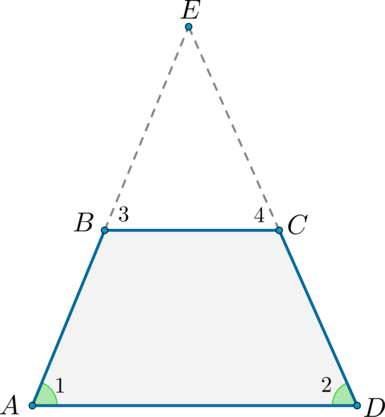
Достроим трапецию до треугольника (AED) как показано на рисунке. Так как (angle 1 = angle 2), то треугольник (AED) равнобедренный и (AE
= ED). Углы (1) и (3) равны как соответственные при параллельных прямых (AD) и (BC) и секущей (AB). Аналогично равны углы (2) и (4), но (angle 1 = angle 2), тогда (angle 3 = angle 1 = angle 2 =
angle 4), следовательно, треугольник (BEC) тоже равнобедренный и (BE = EC).
В итоге (AB = AE – BE = DE – CE = CD), то есть (AB = CD), что и требовалось доказать.
2) Пусть (AC=BD). Т.к. (triangle AODsim triangle BOC), то обозначим их коэффициент подобия за (k). Тогда если (BO=x), то (OD=kx). Аналогично (CO=y Rightarrow AO=ky).
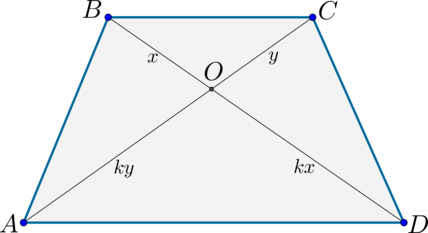
Т.к. (AC=BD), то (x+kx=y+ky Rightarrow x=y). Значит (triangle AOD) – равнобедренный и (angle OAD=angle ODA).
Таким образом, по первому признаку (triangle ABD=triangle ACD) ((AC=BD, angle OAD=angle ODA, AD) – общая). Значит, (AB=CD), чтд.
Источник
Определение
Трапецией называется четырехугольник, у которого две стороны
параллельны, а две другие не параллельны.

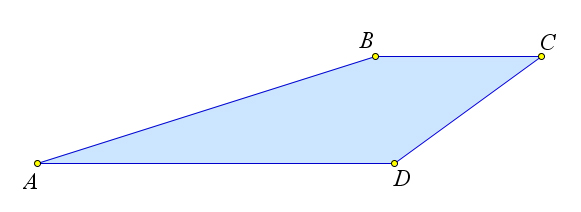
Замечание
Сумма углов при боковой стороне трапеции равна $180^circ$.
Доказательство
Действительно, так как основания трапеции параллельны, а боковая
сторона является секущей, то углы при боковой стороне являются
внутренними односторонними углами при параллельных прямых, и,
следовательно, их сумма равна $180^circ$.
Определение
Трапеция называется равнобедренной, если ее боковые стороны равны.
Трапеция называется прямоугольной, если один из ее углов равен $90^circ$.
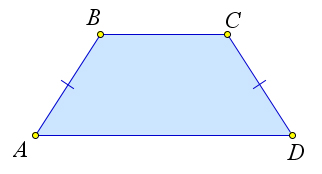
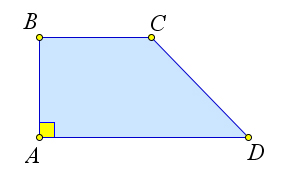
Свойства равнобедренной трапеции
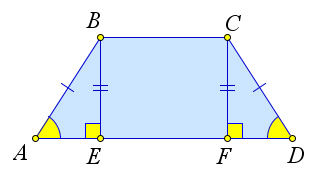
Углы при основании равнобедренной трапеции равны.
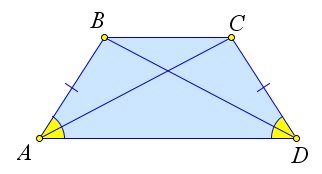
Диагонали равнобедренной трапеции равны.
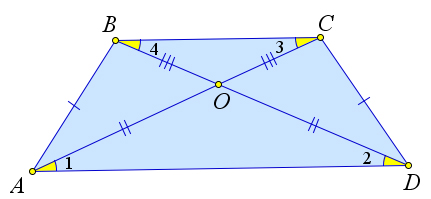
Диагонали равнобедренной трапеции, пересекаясь, образуют два равных и два равнобедренных треугольника.
Проекция боковой стороны равнобедренной трапеции на основание равна полуразности оснований, а проекция диагонали – полусумме оснований.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим равнобедренную трапецию $ABCD$, $AB=CD$.
Докажем, что $angle A=angle D$.
Проведем из точек $B$ и $C$ высоты $BE$ и $CF$.
Треугольники $triangle ABE$ и $triangle CFD$ равны по катету и гипотенузе ($AB=CD,
BE=CF$).
Следовательно, $angle A=angle D$.
Докажем второй пункт теоремы.
В равнобедренной трапеции $ABCD$ рассмотрим треугольники $triangle ABD$ и $triangle ACD$.
Они равны по первому признаку ($AB=CD$, $AD$ – общая, $angle A=angle D$ по
первому пункту).
Следовательно, $AC=BD$.
Докажем третий пункт теоремы.
Пусть диагонали равнобедренной трапеции $ABCD$ пересекаются в точке $O$. Докажем, что треугольники $triangle AOD$ и $triangle BOC$ – равнобедренные, а треугольники $triangle AOB$ и $triangle COD$ равны.
Действительно, во втором пункте уже было доказано, что $triangle ABD=triangle ACD$.
Следовательно, $angle 1=angle 2$, а так как они накрест лежащие с углами $angle 3$ и $angle 4$ соответственно, то $angle 3=angle 4$, что
и означает, что треугольники $triangle AOD$ и $triangle BOC$ – равнобедренные.
Тогда $AO=OD$ и $BO=OC$, и как следствие, $triangle AOB=triangle COD$ по
третьему признаку равенства треугольников.
Докажем четвертый пункт теоремы.
Так как $triangle AEB=triangle CFD$ (по катету и
гипотенузе), то $AE=FD$.
Кроме того, $EF=BC$, следовательно, $AE=dfrac{AD-BC}{2}$ и
$AF=dfrac{AD-BC}{2}+BC=dfrac{AD+BC}{2}$.
Признаки равнобедренной трапеции
Если углы при основании трапеции равны, то она равнобедренная.
Если диагонали трапеции равны, то она равнобедренная.
Доказательство
Докажем первый пункт теоремы.
Рассмотрим трапецию $ABCD$, в которой $angle A=angle D$.
Докажем, что тогда $AB=CD$, то есть трапеция равнобедренная.
Проведем из вершины $C$ отрезок $CE$ параллельный стороне $AB$.
Тогда $angle A=angle CED$, как соответственные углы.
Следовательно, $angle CED=angle D$, а тогда $triangle CED$ – равнобедренный.
А поскольку $AB=CE$ ($ABCE$ – параллелограмм), то $AB=CD$.
Докажем второй пункт теоремы.
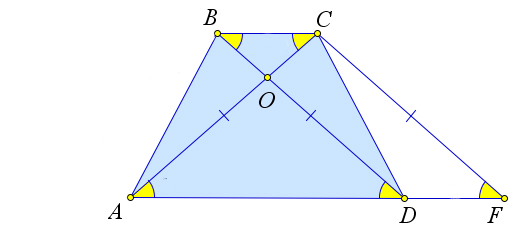
Рассмотрим трапецию $ABCD$, у которой $AC=BD$.
Докажем, что тогда $AB=CD$.
Построим из точки $C$ прямую, параллельный диагонали $BD$. Пусть она пересекает прямую $AD$ в точке $F$.
Тогда $BD=CF$, так как $BCFD$ – параллелограмм по определению.
Тогда $triangle ACF$ – равнобедренный, так как $AC=CF$.
Следовательно $angle OAD=angle ODA$, и $triangle AOD$ – равнобедренный.
Тогда $AO=OD$ и $BO=OC$.
Следовательно, $triangle BOA=triangle COD$ по первому признаку ($angle BOA=angle COD$ – как вертикальные).
Следовательно, $AB=CD$.
Теорема (о равнобедренной трапеции с перпендикулярными диагоналями)
В равнобедренной трапеции со взаимно перпендикулярными диагоналями
высота равна средней линии.
Доказательство
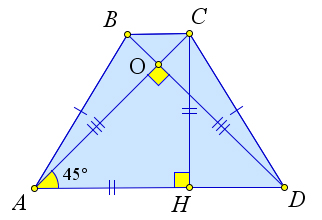
Рассмотрим равнобедренную трапецию $ABCD$, в которой $ACperp BD$.
Докажем, что в такой трапеции высота $CH$ равна средней линии то есть полусумме оснований.
Действительно, $triangle AOD$ – равнобедренный и прямоугольный, следовательно, $angle OAD = 45^circ$. Тогда $triangle AHC$ – равнобедренный, то есть $AH=CH$.
Но отрезок $AH$ равен полусумме оснований.
Источник
