Какие свойства у радиуса

Здравствуйте, уважаемые читатели блога KtoNaNovenkogo.ru.
Сегодня мы продолжим знакомить вас с различными математическими терминами. И расскажем, что такое РАДИУС.
На самом деле эту тему проходят еще в начальных классах обычной школы. И все, кто хорошо учился, сразу смогут сказать, о чем идет речь. Ну, или хотя бы точно понять, что РАДИУС как-то связан с окружностью.
Что такое радиус
И действительно:
Радиус – это отрезок, который начинается в центре окружности и заканчивается в любой точке ее поверхности. В то же время так называется и длина этого отрезка.
Вот так это выглядит графически.
Само слово РАДИУС имеет латинские корни. Оно произошло от «radius», что можно перевести как «луч» или «спица колеса». Впервые этот математический термин ввел французский ученый П.Ромус. Было это в 1569 году.
Но потребовалось чуть более ста лет, чтобы слово РАДИУС прижилось и стало общепринятым.
Кстати, есть еще несколько значений слова РАДИУС:
- Размер охвата чего-нибудь или сфера распространения. Например, говорят «Огонь уничтожил все в радиусе 10 километров» или «ОН показал на карте радиус действия артиллерии»;
- В анатомии этим словом обозначают Лучевую кость предплечья.
Но, конечно, нас интересует РАДИУС как математический термин. А потому и продолжим говорить именно о нем.
Радиус и диаметр
Радиус в математике всегда обозначается латинской буквой «R» или «r». Принципиальной разницы, большую букву писать или маленькую, нет.
А два соединенных вместе радиуса, которые к тому же находятся на одной прямой, называются диаметром. Или по-другому:
Диаметр – это отрезок, который проходит через центр окружности и соединяет две противоположные точки на ее поверхности. По аналогии с радиусом под диаметром подразумевают и длину этого отрезка.
Обозначается диаметр также первой буквой своего слова – D или d.
Исходя из определения диаметра, можно сделать простой вывод, который одновременно является одной из базовых основ геометрии.
А именно:
Длина диаметра равна удвоенной длине радиуса.
Свойства радиуса
В отношении радиуса действуют несколько важных правил:
- Радиус составляет половину диаметра. Это мы продемонстрировали только что.
- У окружности может быть сколько угодно радиусов. Но все они будут равны по длине между собой.
- Если в точке пересечения радиуса с поверхностью окружности провести касательную, то эти две линии будут пересекаться под прямым углом. Доказательство этой теоремы наглядно приводится на следующем рисунке.
Радиус, который перпендикулярен хорде, делит ее на две равные части.
Напомним, хордой называется любой отрезок, который проходит через две точки на поверхности окружности, но не через центр. Этим она принципиально отличается от диаметра.
Длина и площадь окружности через радиус
Об этих математических величинах мы решили рассказать не случайно. Дело в том, что при их вычислении просто необходимо знать значение радиуса. И наоборот, зная длину окружности или ее площадь, можно найти радиус.
Длина окружности
Длина окружности – это кривая, которая состоит из точек, равноудаленных от центра окружности. Проще говоря, это длина поверхности окружности.
Длина окружности одновременно является и ее периметром, а потому в геометрии она обозначается латинской буквой «Р» (иногда встречаются и «L», и «C»). А формула для ее вычисления выглядит следующим образом:
Иногда ее пишут и как P=πD, так как 2R – это удвоенный радиус, что, как мы уже сказали выше, является диаметром. Но классическая формула во всех учебниках дается все-таки через радиус.
Гораздо интереснее здесь рассмотреть величину, обозначаемую буквой π. Это как многим известно, математическая постоянная. Она произносится как «Пи» и равна 3,14.
Хотя на самом деле количество знаков после запятой у «пи» не ограничено. Но для простоты вычислений решено брать именно так.
Площадь окружности
Площадь окружности – это пространство, которое находится внутри ее периметра. Она обозначается латинской буквой «S». А формула для ее вычисления выглядит так:
Опять же, здесь R- это радиус, а π – математическая постоянная, равная 3,14.
Вместо заключения
Чтобы еще больше понять, насколько важно понятие РАДИУС, вспомните инструмент, с помощью которого можно начертить окружность. Это циркуль и выглядит он вот так.
Пользоваться им просто. Ножка с острым концом ставится в центр будущей окружности. А ножка с грифелем прочерчивает линию. А расстояние, на котором они будут друг от друга, и есть РАДИУС.
Удачи вам! До скорых встреч на страницах блога KtoNaNovenkogo.ru
Использую для заработка
- ВоркЗилла – удаленная работа для всех
- Анкетка – платят за прохождение тестов
- Etxt – платят за написание текстов
- Кьюкоммент – биржа комментариев
- Поиск лучшего курса обмена
- 60сек – выгодный обмен криптовалют
- Бинанс – надёжная биржа криптовалют
- ВкТаргет – заработок в соцсетях (ВК, ОК, FB и др.)
Источник
Радиус окружности обозначен красным цветом
Ра́диус (лат. radius — спица колеса, луч) — отрезок, соединяющий центр окружности (или сферы) с любой точкой, лежащей на окружности (или поверхности сферы), а также длина этого отрезка. Радиус составляет половину диаметра.
Энциклопедичный YouTube
1/3
Просмотров:
40 983
7 479
1 936
✪ Как Найти Радиус Сегмента на Потолке. Радиус Окружности По Хорде И Высоте Сегмента
✪ Радиус наблюдаемой Вселенной
✪ Тойргийн радиус, диаметр, хүрээний урт
Здравствуйте.
Меня зовут Роман
я снимал видео, как сделать радиусный багет
из гипса
и мне задали интересный вопрос
как найти радиус на потолке
и перенести его на рабочий стол
Первое, что необходимо сделать
надо отрисовать радиус который на потолке
на каком нибудь листе бумаги
лучше всего подходят самые дешевые обои
но у меня нет
поэтому взял упаковку от плитки
когда приложили, можно поджать, останется след
или отрисовать
получится нарисованный сектор круга
после того как вы перенесли на бумагу
изображение
у вас должна получится вот такая дуга
нарисую на стене
я знаю два способа
как найти радиус окружности по дуге
и сейчас я вам о них расскажу
способ первый
рисую дугу
вот у вас есть длина дуги
или сегмент круга
который у вас нарисован на бумаге
необходимо провести секущую
эта часть называется хордой
делим хорду пополам
на середине под прямым углом провожу линию
эта линия попадёт в центр круга
и понятно если будет ещё пару таких хорд
и сделать такие пересечения они все попадут в центр окружности
рисую ещё две хорды
хорды должны получится одинаковые
измеряю длинну
делим пополам
проводим под прямым углом линии
если точно всё нарисовать
данные линии пересекутся в центре круга
Что получилось у меня
так получилось потому что не точно чертил
измеряю радиус
80см
проверяю радиус
82см
2см это большая разница
но она получилась только потому
что не точно измерил расстояния и не точно начертил прямые углы
но смысл вам будет понятен
как видите в первом случае погрешность
есть и она всегда на практике будет
всё зависит от того на сколько точно вы
сделаете чертёж
но есть и второй способ
погрешность которого составляет 0,12
обозначаем
длину дуги сегмента
хорду
радиус
высоту сегмента
зная эти размеры мы можем найти радиус
радиус равен
в данном случае нам будет гораздо легче всё измерить
нам необходимо знать только две длинны
длинна хорды
109см
и высота сегмента
20.5см
считайте
ладно. давайте вместе
радиус 82.6см
во втором случае вариант
более точный
здесь я не много не точно измерил
и здесь радиус составляет
82.4мм
второй вариант более предпочтительный
и им гораздо легче пользоваться
Если понравилось видео
поставте лайк
оставляйте комментарии
в следующем видео я вам расскажу
как сделать переднюю панель ванны
всем спасибо за просмотр
всем удачи и добра
до новых видео .
Содержание
- 1 Свойства
- 2 Связанные определения
- 3 Этимология
- 4 Обобщения
- 5 См. также
Свойства
- Радиус, проведённый в точку окружности, перпендикулярен касательной к окружности в этой точке.
- Радиус, перпендикулярный хорде, делит её на две равные части
Связанные определения
- Центральный угол в окружности — это угол, образованный двумя радиусами.
- Радиус кривизны кривой — это радиус окружности, имеющей с этой кривой касание второго порядка.
Этимология
Слово «радиус» впервые встречается в 1569 г. у французского учёного П. Ромуса, несколько позже у Ф. Виета. Становится общепринятым лишь в конце XVII века. Происходит от лат. radius, означающего «луч, спица колеса».
Обобщения
Радиусом множества , лежащего в метрическом пространстве с метрикой , называется величина . Например, радиус n-размерного гиперкуба со стороной s равен
См. также
- Атомный радиус
- Боровский радиус
- Гравитационный радиус
- Дебаевский радиус экранирования
- Ионный радиус
- Кристаллохимический радиус
- Радиус инерции
- Радиус-вектор
- Радиус поражения
- Радиус действия
- Радиус поворота
- Радиус ротации
- Сферический радиус
Источник
- Математическая энциклопедия
О к р у ж н о с т и — отрезок, соединяющий точку окружности (или сферы) с центром. Р. наз. также длину этого отрезка. БСЭ-3.
Источник:
Математическая энциклопедия
на Gufo.me
Значения в других словарях
- радиус —
РАДИУС, а, м. 1. В математике: отрезок прямой, соединяющий центр шара или круга с любой точкой сферы или окружности, а также длина этого отрезка. 2. перен. Охват, область распространения чего-н. Р. действия авиации. | прил. радиусный, ая, ое (спец.).
Толковый словарь Ожегова - РАДИУС —
РАДИУС, в геометрии — расстояние или прямая от центра окружности или сферы к любой точке ОКРУЖНОСТИ или поверхности сферы.
Научно-технический словарь - радиус —
-а, м. 1. мат. Отрезок прямой, соединяющий какую-л. точку окружности или поверхности шара с центром, а также длина этого отрезка. 2. перен. Величина охвата, сфера действия, распространения чего-л. (по отношению к какому-л. центру).
Малый академический словарь - радиус —
Радиуса, м. [латин. radius – луч, спица]. 1. Прямая, соединяющая точку центра с любой точкой окружности или поверхности шара (мат.). 2. перен. Величина охвата чего-н., сфера распространения чего-н. (по отношению к какому-н. центру; книжн.). Радиус действия. 3. Лучевая кость предплечья (анат.).
Большой словарь иностранных слов - радиус —
РАДИУС м. лат. полупоперечник круга, полуось шара, луч, нога, которою круг очерчен; черта или мера от остья (средоточия, центра) до обода. Радиус вектор, полупоперечник долгокруга (эллипса). || Радиус, лучевая кость; она лежит рядом с локтевою и с нею образует локтевую часть руки (локотник).
Толковый словарь Даля - радиус —
Заимств. в Петровскую эпоху из лат. яз., где radius «радиус» < «луч».
Этимологический словарь Шанского - радиус —
сущ., кол-во синонимов: 2 критрадиус 1 отрезок 12
Словарь синонимов русского языка - Радиус —
Окружности (или сферы) (лат. radius, буквально— спица колеса, луч), отрезок, соединяющий точку окружности (или сферы) с центром. Р. называют также длину этого отрезка.
Большая советская энциклопедия - радиус —
РАДИУС -а; м. [лат. radius] 1. Матем. Отрезок прямой, соединяющий какую-л. точку окружности или поверхности шара с центром; длина этого отрезка. 2. Величина охвата, сфера действия, распространения чего-л. (по отношению к какому-л. центру). Р. действия авиации. ◁ Радиусный, -ая, -ое.
Толковый словарь Кузнецова - радиус —
РАДИУС – Р. виража беговой дорожки. Величина радиуса кривизны виража по внутреннему контуру беговой дорожки стадиона, манежа. – Р. виража санно-бобслейной трассы. Величина радиуса кривизны трассы по ее внутреннему контуру.
Словарь спортивных терминов - радиус —
ра́диус уже в 1720 г., Уст. морск. (Смирнов 251). Через голл. radius из лат. radius “радиус; луч” (Преобр. II, 172).
Этимологический словарь Макса Фасмера - РАДИУС —
РАДИУС (лат. radius, букв. — спица колеса, луч) — отрезок, соединяющий какую-либо точку окружности или сферы с центром, а также длина этого отрезка.
Большой энциклопедический словарь - радиус —
орф. радиус, -а
Орфографический словарь Лопатина - радиус —
радиус м. 1. Отрезок прямой, соединяющий центр окружности или шара с какой-либо точкой окружности или поверхности шара. 2. перен. Область распространения, величина охвата чего-либо.
Толковый словарь Ефремовой - радиус —
Ра́диус/.
Морфемно-орфографический словарь - радиус —
Радиус, радиусы, радиуса, радиусов, радиусу, радиусам, радиус, радиусы, радиусом, радиусами, радиусе, радиусах
Грамматический словарь Зализняка - радиус —
Р’АДИУС, радиуса, ·муж. (·лат. radius — луч, спица). 1. Прямая, соединяющая точку центра с любой точкой окружности или поверхности шара (мат.). 2. перен.
Толковый словарь Ушакова

Источник
Определение. Окружность — это совокупность всех точек на плоскости, которые находятся на одинаковом расстоянии от заданной точки О, которая называется центром окружности.
Определение. Единичная окружность – окружность, радиус которой равна единице.
Определение. Круг – часть плоскости, ограничена окружностью.
Определение. Радиус окружности R – расстояние от центра окружности О до любой точки окружности.
Определение. Диаметр окружности D – отрезок, который соединяет две точки окружности и проходит через ее центр.
Основные свойства окружности
1. Диаметр окружности равен двум радиусам.
D = 2r
2. Кратчайшее расстояние от центра окружности к секущей (хорде) всегда меньше радиуса.
3. Через три точки, которые не лежат на одной прямым, можно провести только одну окружность.
4. Среди всех замкнутых кривых с одинаковой длиной, окружность имеет наибольшую площадь.
5. Если две окружности соприкасаются в одной точке, то эта точка лежит на прямой, что проходит через центры этих окружностей.
Формулы длины окружности и площади круга
Формулы длины окружности
1. Формула длины окружности через диаметр:
L = πD
2. Формула длины окружности через радиус:
L = 2πr
Формулы площади круга
1. Формула площади круга через радиус:
S = πr2
2. Формула площади круга через диаметр:
S = πD24
Уравнение окружности
1. Уравнение окружности с радиусом r и центром в начале декартовой системы координат:
r2 = x2 + y2
2. Уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
r2 = (x – a)2 + (y – b)2
3. Параметрическое уравнение окружности с радиусом r и центром в точке с координатами (a, b) в декартовой системе координат:
| { | x = a + r cos t |
| y = b + r sin t |
Касательная окружности и ее свойства
Определение. Касательная окружности – прямая, которая касается окружности только в одной точке.
Основные свойства касательных к окружности
1. Касательная всегда перпендикулярна к радиусу окружности, проведенного в точке соприкосновения.
2. Кратчайшее расстояние от центра окружности к касательной равна радиусу окружности.
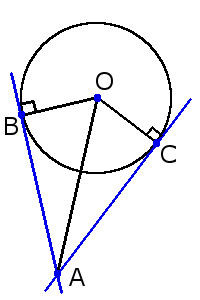
3. Если две касательные, с точками соприкосновения B и C, на одной окружности не параллельны, то они пересекаются в точке A, а отрезок между точкой соприкосновения и точкой пересечения одной касательной равен таком же отрезке на другой касательной:
AB = AC
Также, если провести прямую через центр окружности О и точку пересечения A этих касательных, то углы образованный между этой прямой и касательными будут равны:
∠ОAС = ∠OAB
Секущая окружности и ее свойства
Определение. Секущая окружности – прямая, которая проходит через две точки окружности.
Основные свойства секущих

1. Если с точки вне окружности (Q) выходят две секущие, которые пересекают окружность в двух точках A и B для одной секущей и C и D для другой секущей, то произведения отрезков двух секущих равны между собою:
AQ ∙ BQ = CQ ∙ DQ

2. Если из точки Q вне окружности выходит секущая прямая, что пересекает окружность в двух точках A и B, и касательная с точкой соприкосновения C, то произведение отрезков секущей равна квадрату длины отрезка касательной:
AQ ∙ BQ = CQ2
Хорда окружности ее длина и свойства
Определение. Хорда окружности – отрезок, который соединяет две точки окружности.
Длина хорды

1. Длина хорды через центральный угол и радиус:
AB = 2r sin α2

2. Длина хорды через вписанный угол и радиус:
AB = 2r sin α
Основные свойства хорд

1. Две одинаковые хорды стягивают две одинаковые дуги:
если хорды AB = CD, то
дуги ◡ AB = ◡ CD
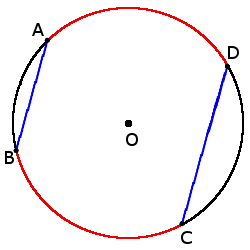
2. Если хорды параллельные, то дуги между ними будут одинаковые:
если хорды AB ∣∣ CD, то
◡ AD = ◡ BC
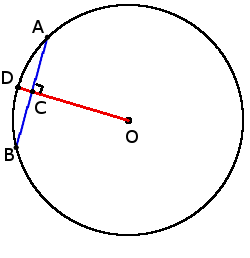
3. Если радиус окружности перпендикулярен к хорде, то он разделяет хорду пополам в точке их пересечения:
если OD ┴ AB, то
AC = BC
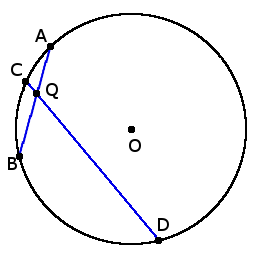
4. Если две хорды AB и CD пересекаются в точке Q, то произведение отрезков, что образовались при пересечении, одной хорды равны произведению отрезков другой хорды:
AQ ∙ BQ = DQ ∙ QC
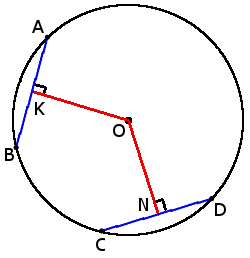
5. Хорды с одинаковой длиной находятся на одинаковом расстоянии от центра окружности.
если хорды AB = CD, то
ON = OK
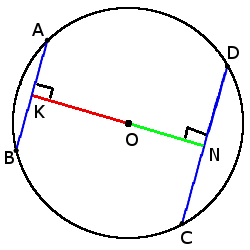
6. Чем больше хорда тем ближе она к центру.
если CD > AB, то
ON < OK
Центральный угол, вписанный угол и их свойства
Определение. Центральный угол окружности – угол, вершиной которого есть центр окружности.
Определение. Угол вписанный в окружность – угол, вершина которого лежит на окружности, а стороны угла пересекают окружность.
Основные свойства углов
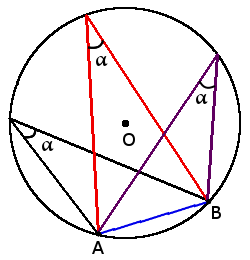
1. Все вписанные углы, которые опираются на одну дугу – равны.
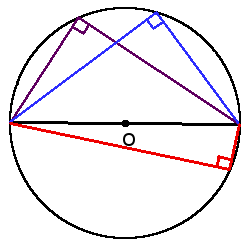
2. Вписанний угол, который опирается на диаметр будет прямым (90°).

3. Вписанный угол равен половине центрального угла, что опирается на ту же дугу
β = α2

4. Если два вписанных угла опираются на одну хорду и находятся по различные стороны от нее, то сумма этих углов равна 180°.
α + β = 180°
Определение. Дуга окружности (◡) – часть окружности, которая соединяет две точки на окружности.
Определение. Градусная мера дуги – угол между двумя радиусами, которые ограничивают эту дугу. Градусная мера дуги всегда равна градусной мере центрального угла, который ограничивает эту дугу своими сторонами.
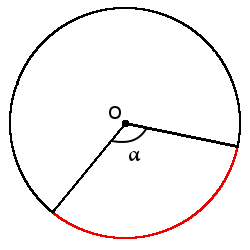
Формула длины дуги через центральный угол (в градусах):
l = πr180°∙ α
Определение. Полуокружность – дуга в которой концы соединены диаметром окружности.
Определение. Полукруг (◓) – часть круга, которая ограничена полуокружностью и диаметром.
Определение. Сектор (◔) – часть круга, которая ограничена двумя радиусами и дугой между этими радиусами.

Формула. Формула площади сектор через центральный угол (в градусах)
S = πr2360°∙ α
Определение. Сегмент – часть круга, которая ограничена дугой и хордой, что соединяет ее концы.
Определение. Концентрические окружности – окружности с различными радиусами, которые имеют общий центр.
Определение. Кольцо – часть плоскости ограниченная двумя концентрическими окружностями.
Источник
