Какие свойства у пределов
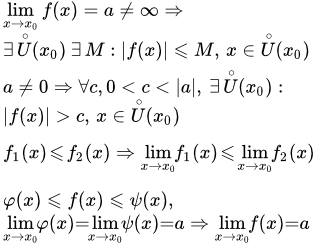
Формулировки свойств
Далее мы считаем, что рассматриваемые функции определены в соответствующей окрестности точки x0. Точка x0 может являться конечным числом или одним из символов бесконечности: . Окрестность может быть как двусторонней для двусторонних пределов, так и односторонней для односторонних.
Влияние значений функции в конечном числе точек на величину предела
Если значения функции f(x) изменить (или сделать неопределенными) в конечном числе точек x1, x2, x3, … xn, то это изменение никак не повлияет на существование и величину предела функции в произвольной точке x0.
Доказательство ⇓
Теорема об ограниченности функции, имеющей конечный предел
Если существует конечный предел , то существует такая проколотая окрестность точки x0, в которой функция f(x) ограничена:
.
Доказательство ⇓
Теорема об ограниченности снизу функции, имеющей ненулевой предел
Пусть функция f(x) имеет в точке x0 конечный предел, отличный от нуля:
.
Тогда, для любого числа c из интервала , существует такая проколотая окрестность точки x0, что для всех x, принадлежащих этой окрестности: ,
, если ;
, если .
Доказательство ⇓
Свойство о пределе постоянной функции
Если в некоторой проколотой окрестности точки , – постоянная, то .
Доказательство ⇓
Свойство о равенстве односторонних пределов
Функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке равные односторонние пределы.
Доказательство ⇓
Свойство пределов функций, связанных неравенством
Если существуют конечные пределы и и в некоторой проколотой окрестности точки x0
,
то .
Доказательство ⇓
Заметим, что если функции удовлетворяют строгому неравенству , то их пределы все равно связаны нестрогим неравенством .
Свойство неравенств бесконечно больших функций
Если , и в некоторой проколотой окрестности точки
,
то .
Доказательство
В частности, если в некоторой проколотой окрестности точки
,
то если , то и ;
если , то и .
Теорема о промежуточной функции
Если в некоторой проколотой окрестности конечной, или бесконечно удаленной точки x0, выполняются неравенства:
,
и существуют конечные (или бесконечные определенного знака) равные пределы:
, то существует предел функции :
.
Доказательство
Теорема о функциях, пределы которых связаны неравенством
Пусть существуют конечные пределы функций и :
и ,
где – конечное число или бесконечно удаленная точка. Если эти пределы связаны неравенством , то существует такая проколотая окрестность точки , в которой
.
Доказательство ⇓
Доказательство свойств
Влияние значений функции в конечном числе точек на величину предела
Все свойства ⇑ Если значения функции f(x) изменить (или сделать неопределенными) в конечном числе точек x1, x2, x3, … xn, то это изменение никак не повлияет на существование и величину предела функции в произвольной точке x0.
Доказательство
Это следует из того, что в определение предела функции входят только значения независимой переменной из произвольной проколотой окрестности точки x0. Значение функции в самой точке x0 полностью исключается из рассмотрения. Функция может быть определена в этой точке, или не определена – на существование и величину предела в точке x0 это никакого влияния оказать не может.
Таким образом, если одна из точек, в которых производятся изменения значений функции, совпадает с x0, то это не может оказать влияния на величину или существование предела. Но, поскольку проколотая окрестность точки x0 выбирается произвольно, то мы всегда можем сузить ее границы, чтобы в нее не попали остальные точки, поскольку их число конечно. Поэтому, при вычислении предела, значения функции в конечном числе точек, не оказывают влияния на величину или существование предела в произвольной точке.
Теорема об ограниченности функции, имеющей конечный предел
Все свойства ⇑ Если существует конечный предел , то существует такая проколотая окрестность точки x0, в которой функция f(x) ограничена:
.
Доказательство
Пусть существует конечный предел
.
Воспользуемся определением предела функции по Коши.
Согласно этому определению, для любой окрестности точки a, существует такая проколотая окрестность точки , что для всех x, принадлежащих этой проколотой окрестности: , значения функции принадлежат окрестности точки a:
.
Поскольку число a конечно, то в качестве окрестности точки a возьмем ее ε – окрестность с : .
Тогда существует проколотая окрестность точки , так что для всех x, принадлежащих этой окрестности,
при .
Выполняем преобразования:
;
;
;
.
Итак, мы показали, что существует окрестность , для которой
при ,
где .
Теорема доказана.
Теорема об ограниченности снизу функции, имеющей ненулевой предел
Все свойства ⇑ Пусть функция f(x) имеет в точке x0 конечный предел, отличный от нуля:
.
Тогда, для любого числа c из интервала , существует такая проколотая окрестность точки x0, что для всех x, принадлежащих этой окрестности: ,
, если ;
, если .
Доказательство
Пусть существует конечный предел, отличный от нуля
.
Воспользуемся определением предела функции по Коши.
Согласно этому определению, для любой окрестности точки a, существует такая проколотая окрестность точки , что для всех x, принадлежащих этой проколотой окрестности: , значения функции принадлежат окрестности точки a:
.
В качестве окрестности точки a возьмем ее ε – окрестность:
.
Поскольку ε есть произвольное положительное число, то положим . Тогда существует проколотая окрестность точки , так что для всех x, принадлежащих этой окрестности,
при .
Раскрываем знак модуля и выполняем преобразования:
;
.
При , . Тогда
.
При , . Тогда
.
Теорема доказана.
Свойство о пределе постоянной функции
Все свойства ⇑ Если в некоторой проколотой окрестности точки , – постоянная, то .
Доказательство
Пусть, на некоторой проколотой окрестности точки , функция является постоянной:
при .
Тогда в этой окрестности, для любого положительного ,
.
То есть для любого , существует такая проколотая окрестность точки , совпадающая с , для всех точек которой
при .
Согласно определению Коши это означает, что
.
Свойство доказано.
Свойство о равенстве односторонних пределов
Все свойства ⇑ Функция имеет предел в точке тогда и только тогда, когда она имеет в этой точке равные односторонние пределы.
Доказательство
Пусть существует конечный или бесконечный предел функции f в конечной или бесконечно удаленной точке :
.
Покажем, что существуют односторонние пределы, равные a.
Воспользуемся определением предела функции по Коши с использованием произвольных окрестностей. Согласно этому определению, для любой окрестности точки a, существует такая проколотая окрестность точки , на которой определена и
для всех .
Но двустороннюю проколотую окрестность можно представить как объединение левой и правой проколотых окрестностей. Тогда
для всех ;
для всех .
Это означает, что существуют односторонние равные пределы:
.
Для бесконечно удаленной точки , под символами и мы понимаем и , соответственно.
Пусть теперь существуют равные односторонние пределы. Поскольку существует предел слева, то для любой окрестности точки a, существует такая проколотая левая окрестность точки , на которой определена и
для всех .
Поскольку существует предел справа, то для той же окрестности точки a, существует такая проколотая правая окрестность точки , на которой определена и
для всех .
Объединив окрестности и , получим проколотую двустороннюю, или просто проколотую окрестность точки :
.
Тогда, для выбранной нами произвольной окрестности ,
для всех .
Это означает, что
.
Свойство доказано.
Свойство пределов функций, связанных неравенством
Все свойства ⇑ Если существуют конечные пределы и и в некоторой проколотой окрестности точки x0
,
то .
Доказательство
Пусть есть произвольная последовательность, сходящаяся к : . И пусть ее элементы принадлежат проколотой окрестности точки , на которой выполняется неравенство
.
Рассмотрим последовательности и . Поскольку и , то согласно определению предела функции по Гейне, эти последовательности имеют пределы:
, .
Поскольку , то их элементы связаны неравенствами:
.
Тогда, согласно свойству неравенств,
.
Отсюда
.
Свойство доказано.
Теорема о функциях, пределы которых связаны неравенством
Все свойства ⇑ Пусть существуют конечные пределы функций и :
и ,
где – конечное число или бесконечно удаленная точка. Если эти пределы связаны неравенством , то существует такая проколотая окрестность точки , в которой
.
Доказательство
Для доказательства будем использовать универсальное определение предела функции по Коши.
Поскольку существует конечный предел , то для любого положительного , существует такая проколотая окрестность точки , в которой значения функции принадлежат ε – окрестности точки :
.
Поскольку существует конечный предел , то для любого положительного , существует такая проколотая окрестность точки , в которой значения функции принадлежат ε – окрестности точки :
.
Возьмем .
И пусть – пересечение окрестностей и :
, где .
Тогда для всех выполняются неравенства:
;
.
Раскроем знаки модуля:
;
.
К первому неравенству прибавим и оставим только правую часть. Ко второму неравенству прибавим и оставим только левую часть. В результате получаем:
;
.
Отсюда следует:
.
Или
при ,
где , .
Теорема доказана.
Использованная литература:
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: 26-05-2018 Изменено: 27-09-2020
Источник
Определение предела функции
Первое определение предела функции по Гейне
Предел функции (по Гейне) при ее аргументе x, стремящемся к x0 – это такое конечное число или бесконечно удаленная точка a, для которой выполняются следующие условия:
1) существует такая проколотая окрестность точки x0, на которой функция f(x) определена;
2) для любой последовательности , сходящейся к :
,
элементы которой принадлежат окрестности , последовательность сходится к a:
.
Предел функции обозначают так:
.
Или при .
Здесь a и x0 могут быть как конечными числами, так и бесконечно удаленными точками: .
Для бесконечно удаленных точек приняты следующие обозначения:
.
Проколотая окрестность конечной точки может быть как двусторонней, так и односторонней. В последнем случае, для левой окрестности пишут:
.
Для правой окрестности:
.
С помощью логических символов существования и всеобщности это определение можно записать следующим образом:
.
См. «Универсальное определение предела функции по Гейне и по Коши».
Второе определение по Коши
Предел функции (по Коши) при ее аргументе x, стремящемся к x0 – это такое конечное число или бесконечно удаленная точка a, для которой выполняются следующие условия:
1) существует такая проколотая окрестность точки x0, на которой функция f(x) определена;
2) для любой окрестности точки a, принадлежащей , существует такая проколотая окрестность точки x0, на которой значения функции принадлежат выбранной окрестности точки a:
при .
Здесь a и x0 также могут быть как конечными числами, так и бесконечно удаленными точками. С помощью логических символов существования и всеобщности это определение можно записать следующим образом:
.
Если в качестве множества взять левую или правую окрестность конечной точки, то получим определение предела по Коши слева или справа.
Теорема
Определения предела функции по Коши и по Гейне эквивалентны.
Доказательство
Применяемые окрестности точек
В приведенном выше определении применяются произвольные окрестности точек. Например, проколотой окрестностью конечной точки является множество , где – два положительных числа, которые определяют размер окрестности. Более подробно, см. «Окрестность точки».
Тогда, фактически, определение по Коши означает следующее.
Для любых положительных чисел , существуют числа , так что для всех x, принадлежащих проколотой окрестности точки : , значения функции принадлежат окрестности точки a: ,
где , .
С таким определением не совсем удобно работать, поскольку окрестности определяются с помощью четырех чисел . Но его можно упростить, если ввести окрестности с равноудаленными концами. То есть можно положить , . Тогда мы получим определение, которое проще использовать при доказательстве теорем. При этом оно является эквивалентным определению, в котором используются произвольные окрестности. Доказательство этого факта приводится в разделе «Эквивалентность определений предела функции по Коши».
Тогда можно дать единое определение предела функции в конечных и бесконечно удаленных точках:
.
Здесь для конечных точек
; ;
.
Любые окрестности бесконечно удаленных точек являются проколотыми:
; ; .
См. «Окрестность точки»
Далее мы приводим формулировки определений предела функции по Коши для разных случаев, используя определения окрестностей с равноудаленными концами.
Конечные пределы функции в конечных точках
Число a называется пределом функции f(x) в точке x0, если
1) функция определена на некоторой проколотой окрестности конечной точки ;
2) для любого существует такое , зависящее от , что для всех x, для которых , выполняется неравенство
.
С помощью логических символов существования и всеобщности определение предела функции можно записать следующим образом:
.
Односторонние пределы.
Левый предел в точке (левосторонний предел):
.
Правый предел в точке (правосторонний предел):
.
Пределы слева и справа часто обозначают так:
; .
См. «Определение предела функции в конечной точке»
Конечные пределы функции в бесконечно удаленных точках
Аналогичным образом определяются пределы в бесконечно удаленных точках.
.
.
.
См. «Определение предела функции на бесконечности»
Бесконечные пределы функции
.
Также можно ввести определения бесконечных пределов определенных знаков, равных и :
.
.
Свойства и теоремы предела функции
Далее мы считаем, что рассматриваемые функции определены в соответствующей проколотой окрестности точки , которая является конечным числом или одним из символов: . Также может быть точкой одностороннего предела, то есть иметь вид или . Окрестность является двусторонней для двустороннего предела и односторонней для одностороннего.
Основные свойства
Если значения функции f(x) изменить (или сделать неопределенными) в конечном числе точек x1, x2, x3, … xn, то это изменение никак не повлияет на существование и величину предела функции в произвольной точке x0.
Если существует конечный предел , то существует такая проколотая окрестность точки x0, на которой функция f(x) ограничена:
.
Пусть функция имеет в точке x0 конечный предел, отличный от нуля:
.
Тогда, для любого числа c из интервала , существует такая проколотая окрестность точки x0, что для ,
, если ;
, если .
Если, на некоторой проколотой окрестности точки , – постоянная, то .
Если существуют конечные пределы и и на некоторой проколотой окрестности точки x0
,
то .
Если , и на некоторой окрестности точки
,
то .
В частности, если на некоторой окрестности точки
,
то если , то и ;
если , то и .
Если на некоторой проколотой окрестности точки x0:
,
и существуют конечные (или бесконечные определенного знака) равные пределы:
, то
.
Доказательства основных свойств приведены на странице
«Основные свойства предела функции».
Арифметические свойства предела функции
Пусть функции и определены в некоторой проколотой окрестности точки . И пусть существуют конечные пределы:
и .
И пусть C – постоянная, то есть заданное число. Тогда
;
;
;
, если .
Если , то .
Доказательства арифметических свойств приведены на странице
«Арифметические свойства предела функции».
Критерий Коши существования предела функции
Теорема
Для того, чтобы функция , определенная на некоторой проколотой окрестности конечной или бесконечно удаленной точки x0, имела в этой точке конечный предел, необходимо и достаточно, чтобы для любого ε > 0 существовала такая проколотая окрестность точки x0, что для любых точек и из этой окрестности, выполнялось неравенство:
.
«Доказательство критерия Коши».
Предел сложной функции
Теорема о пределе сложной функции
Пусть функции и имеют пределы:
;
.
И пусть существует такая проколотая окрестность точки , на которой
.
Тогда существует предел сложной функции , и он равен :
.
Здесь – конечные или бесконечно удаленные точки: . Окрестности и соответствующие им пределы могут быть как двусторонние, так и односторонние.
Доказательство
Теорема о пределе сложной функции применяется в том случае, когда функция не определена в точке или имеет значение, отличное от предельного . Для применения этой теоремы, должна существовать проколотая окрестность точки , на которой множество значений функции не содержит точку :
.
Если функция непрерывна в точке , то знак предела можно применять к аргументу непрерывной функции:
.
Далее приводится теорема, соответствующая этому случаю.
Теорема о пределе непрерывной функции от функции
Пусть существует предел функции t = g(x) при x → x0, и он равен t0:
.
Здесь точка x0 может быть конечной или бесконечно удаленной: .
И пусть функция f(t) непрерывна в точке t0.
Тогда существует предел сложной функции f(g(x)), и он равен f(t0):
.
Доказательство теоремы приводится на странице
«Предел и непрерывность сложной функции».
Бесконечно малые и бесконечно большие функции
Бесконечно малые функции
Определение
Функция называется бесконечно малой при , если
.
Сумма, разность и произведение конечного числа бесконечно малых функций при является бесконечно малой функцией при .
Произведение функции, ограниченной на некоторой проколотой окрестности точки , на бесконечно малую при является бесконечно малой функцией при .
Для того, чтобы функция имела конечный предел , необходимо и достаточно, чтобы
,
где – бесконечно малая функция при .
Доказательства свойств изложены в разделе
«Свойства бесконечно малых функций».
Бесконечно большие функции
Определение
Функция называется бесконечно большой при , если
.
Свойства бесконечно больших функций
Сумма или разность ограниченной функции, на некоторой проколотой окрестности точки , и бесконечно большой функции при является бесконечно большой функцией при .
Если функция является бесконечно большой при , а функция – ограничена, на некоторой проколотой окрестности точки , то
.
Если функция , на некоторой проколотой окрестности точки , удовлетворяет неравенству:
,
а функция является бесконечно малой при :
, и (на некоторой проколотой окрестности точки ), то
.
Cм. также: Свойства неравенств с бесконечно большими функциями ⇑.
Доказательства свойств изложены в разделе
«Свойства бесконечно больших функций».
Связь между бесконечно большими и бесконечно малыми функциями
Из двух предыдущих свойств вытекает связь между бесконечно большими и бесконечно малыми функциями.
Если функция являются бесконечно большой при , то функция является бесконечно малой при .
Если функция являются бесконечно малой при , и , то функция является бесконечно большой при .
Связь между бесконечно малой и бесконечно большой функцией можно выразить символическим образом:
, .
Если бесконечно малая функция имеет определенный знак при , то есть положительна (или отрицательна) на некоторой проколотой окрестности точки , то этот факт можно выразить так:
.
Точно также если бесконечно большая функция имеет определенный знак при , то пишут:
.
Тогда символическую связь между бесконечно малыми и бесконечно большими функциями можно дополнить следующими соотношениями:
, ,
, .
Дополнительные формулы, связывающие символы бесконечности, можно найти на странице
«Бесконечно удаленные точки и их свойства».
Пределы монотонных функций
Определение
Функция , определенная на некотором множестве действительных чисел X называется строго возрастающей, если для всех таких что выполняется неравенство:
.
Соответственно, для строго убывающей функции выполняется неравенство:
.
Для неубывающей:
.
Для невозрастающей:
.
Отсюда следует, что строго возрастающая функция также является неубывающей. Строго убывающая функция также является невозрастающей.
Функция называется монотонной, если она неубывающая или невозрастающая.
Теорема
Пусть функция не убывает на интервале , где .
Если она ограничена сверху числом M: , то существует конечный предел . Если не ограничена сверху, то .
Если ограничена снизу числом m: , то существует конечный предел . Если не ограничена снизу, то .
Если точки a и b являются бесконечно удаленными, то в выражениях под знаками пределов подразумевается, что .
Эту теорему можно сформулировать более компактно.
Пусть функция не убывает на интервале , где . Тогда существуют односторонние пределы в точках a и b:
;
.
Аналогичная теорема для невозрастающей функции.
Пусть функция не возрастает на интервале , где . Тогда существуют односторонние пределы:
;
.
Доказательство теоремы изложено на странице
«Пределы монотонных функций».
Определение функции
Функцией y = f(x) называется закон (правило), согласно которому, каждому элементу x множества X ставится в соответствие один и только один элемент y множества Y.
Элемент x ∈ X называют аргументом функции или независимой переменной.
Элемент y ∈ Y называют значением функции или зависимой переменной.
Множество X называется областью определения функции.
Множество элементов y ∈ Y, которые имеют прообразы в множестве X, называется областью или множеством значений функции.
Более подробно, см. страницы: «Определение функции»; «Способы задания функций».
Далее, если это особо не оговорено, мы рассматриваем функции, области определения и множества значений которых принадлежат множеству действительных чисел.
Действительная функция называется ограниченной сверху (снизу), если существует такое число M, что для всех выполняется неравенство:
.
Числовая функция называется ограниченной, если существует такое число M, что для всех :
.
Верхней гранью или точной верхней границей действительной функции называют наименьшее из чисел, ограничивающее область ее значений сверху. То есть это такое число s, для которого для всех и для любого , найдется такой аргумент , значение функции от которого превосходит s′: .
Верхняя грань функции может обозначаться так:
.
Соответственно нижней гранью или точной нижней границей действительной функции называют наибольшее из чисел, ограничивающее область ее значений снизу. То есть это такое число i, для которого для всех и для любого , найдется такой аргумент , значение функции от которого меньше чем i′: .
Нижняя грань функции может обозначаться так:
.
Использованная литература:
Л.Д. Кудрявцев. Курс математического анализа. Том 1. Москва, 2003.
С.М. Никольский. Курс математического анализа. Том 1. Москва, 1983.
Автор: Олег Одинцов. Опубликовано: 04-04-2018 Изменено: 09-06-2020
Источник
