Какие свойства у поверхностного слоя жидкости
Вещество, находящееся в жидком состоянии, характеризуется крайне плотным расположением молекул друг относительно друга. Отличаясь от твердых кристаллических тел, чьи молекулы формируют упорядоченные структуры по всему объему кристалла и ограничены в своих тепловых колебаниях фиксированными центрами, молекулы жидкости обладают значительной степенью свободы. Любая конкретная молекула жидкого вещества, как это происходит и в твердых телах, «зажата» соседними молекулами и может совершать тепловые колебания поблизости с некоторым положением равновесия. Несмотря на это, в какой-то момент, любая молекула может переместиться на соседнее вакантное место. Подобные перемещения в жидкостях происходят довольно часто, благодаря чему молекулы не привязаны к конкретным центрам, как в кристаллах, а имеют возможность перемещаться по всему объему жидкости. Именно на этом факте основывается текучесть жидкостей.
Определение 1
По причине сильного взаимодействия между близко расположенными молекулами они могут образовывать локальные, то есть неустойчивые, упорядоченные группы, включающие в себя несколько молекул. Данное явление носит название ближнего порядка (рис. 3.5.1).
Рисунок 3.5.1. Пример ближнего порядка молекул жидкости и дальнего порядка молекул кристаллического вещества: 1 – вода; 2 – лед.
Свойства жидкостей
На рисунке 3.5.2, на примере воды, проиллюстрировано различие между газообразным веществом и жидкостью. Молекула воды H2O включает в свой состав один атом кислорода и два атома водорода, которые расположены под углом 104°. В среднем, расстояние между молекулами пара в десятки раз больше, чем между молекулами воды. На рисунке 3.5.2, в отличие от рисунка 3.5.1, на котором молекулы воды представляют из себя шарики, дается представление о структуре молекулы воды.
Рисунок 3.5.2.Водяной пар (1) и вода (2). Молекулы воды увеличены примерно в 5·107 раз.
Сжимаемость жидкостей, то есть изменение объема вещества при изменении давления, по причине плотности расположения молекул в десятки и сотни тысяч раз меньше, чем сжимаемость газов. К примеру, чтобы изменить объем воды всего на 1 % необходимо повысить значение давления примерно в 200 раз. Подобное увеличение давления по сравнению с атмосферным достигается на глубине близкой к 2 км.
Подобно твердым телам, жидкости имеют свойство менять свой объем при изменении температуры. В случае не самых больших интервалов температур относительное изменение объема ΔVV0 пропорционально изменению температуры ΔT, что может быть записано в виде следующего соотношения:
ΔVV0=β∆T.
В котором коэффициент β представляет собой температурный коэффициент объемного расширения. Данный коэффициент у жидкостей в десятки раз превышает значение такого же у твердых тел.
Пример 1
К примеру, у воды в случае, если температура равна 20 °С βв≈2·10–4 К–1, у стали βст≈3,6·10–5 К–1, у кварцевого стекла βкв≈9·10–6 К–1.
Тепловое расширение воды обладает важным для жизни на Земле эффектом. В условиях температуры ниже 4 °С вода начинает расширяется при снижении температуры β<0. Максимальную плотность ρв=103 кг/м3 вода приобретает при температуре 4 °С.
Замерзая, вода расширяется, из-за чего лед продолжает плавать на поверхности замерзающего водоема. Температура замерзающей воды подо льдом эквивалентна величине в 0 °С. У дна водоема, то есть слоях воды, обладающих большей плотностью, температура держится около 4 °С.
Поверхностное натяжение
Наличие свободной поверхности в жидкостях является одной из самых интересных ее особенностей. В отличие от газов, жидкость не заполняет весь объем сосуда, в котором она находится. Между жидкостью и газом, возможно паром, возникает граница раздела, находящаяся в особых условиях по сравнению с остальной массой жидкости. В отличие от молекул в глубине жидкости, молекулы, располагающиеся в пограничном ее слое, окружены другими молекулами этой же жидкости не со всех сторон. В среднем воздействующие на одну из молекул внутри жидкости со стороны соседних молекул силы межмолекулярного взаимодействия взаимно скомпенсированы. Каждая отдельно взятая молекула в пограничном слое притягивается находящимися внутри жидкости молекулами. При этом, силами, которые оказывают воздействие на такую молекулу жидкости со стороны молекул газа можно пренебречь. Вследствие этого возникает некая направленная вглубь жидкости равнодействующая сила. Поверхностные молекулы втягиваются внутрь жидкости, с помощью действия сил межмолекулярного притяжения. Однако все молекулы, в том числе и принадлежащие пограничному слою, должны находиться в состоянии равновесия. Оно достигается за счет сокращения расстояния между молекулами в пограничном слое и ближайшими их соседями в жидкости. Как проиллюстрировано на рисунке 3.1.2, в процессе уменьшения расстояния расстояния между молекулами появляются силы отталкивания. В случае, когда средняя величина расстояния между молекулами в жидкости равна r0, молекулы поверхностного слоя расположены плотнее, и по этой причине по сравнению с внутренними молекулами они имеют дополнительным запас потенциальной энергии, что можно увидеть на рисунке 3.1.2.
Замечание 1
Стоит обратить внимание на то, что более плотного поверхностного слоя не приводит к сколь-нибудь заметному изменению объема жидкости по причине чрезвычайно низкой сжимаемости.
Силы межмолекулярного взаимодействия совершают положительную работу, в случае, когда молекула перемещается с поверхности внутрь жидкости. И наоборот, чтобы достать некоторое количество молекул на поверхность из глубины жидкости, то есть повысить площадь поверхности жидкости, внешним силам необходимо произвести пропорциональную изменению ΔS площади поверхности положительную работу ΔAвнеш:
ΔAвнеш=σ∆S,
где коэффициент σ носит название коэффициента поверхностного натяжения (σ>0).
Определение 2
Из всего вышесказанного следует, что коэффициент поверхностного натяжения – это величина равная работе, необходимой для увеличения площади поверхности жидкости при постоянной температуре на единицу.
В СИ коэффициент поверхностного натяжения измеряется в джоулях на метр квадратный (Дж/м2) или же в ньютонах на метр (1 Н/м=1 Дж/м2).
Таким образом, по сравнению с молекулами внутри жидкости молекулы поверхностного слоя жидкости обладают избыточной потенциальной энергией. Потенциальная энергия Eр поверхности жидкости пропорциональна ее площади и выражается в виде следующей формулы:
Eр=Aвнеш=σS.
Из раздела механики известно, что равновесным состояниям системы соответствует минимальное значение ее потенциальной энергии. Следовательно, свободная поверхность жидкости стремится уменьшить свою площадь. По данной причине свободная капля жидкости принимает шарообразную форму.
Определение 3
Жидкость ведет себя таким образом, будто по касательной к ее поверхности действуют сокращающие данную поверхность силы. Такие силы называются силами поверхностного натяжения.
Силы поверхностного натяжения влияют на поверхность жидкости таким образом, что она становится похожей на упругую растянутую пленку, с той лишь разницей, что упругие силы в пленке зависят от площади ее поверхности, то есть от степени деформированности пленки, а силы поверхностного натяжения, зависимости от площади поверхности жидкости не имеют.
Пример 2
Некоторые жидкости, например, мыльная вода, имеют способность формировать тонкие пленки. Хорошо известные каждому человеку мыльные пузыри обладают правильной сферической формой, в чем также проявляется воздействие сил поверхностного натяжения. В случае, когда в мыльный раствор опускают проволочную рамку с одной подвижной стороной, вся она затягивается пленкой жидкости, как это показано на рисунке 3.5.3.
Рисунок 3.5.3. Подвижная сторона проволочной рамки в равновесии под действием внешней силы Fвн→ и результирующей сил поверхностного натяжения Fн→.
Силы поверхностного натяжения действуют на уменьшение поверхности пленки. Ради равновесия подвижной стороны рамки к ней необходимо приложить внешнюю силу
Fвн→=-Fн→. Если воздействие силы Fвн→ спровоцирует перемещение перекладины на некоторое Δx, то будет произведена работа ΔAвн=FвнΔx=ΔEp=σΔS, где ΔS=2LΔx является увеличением площади поверхности обеих сторон мыльной пленки. По той причине, что модули сил Fвн→ и Fн→ эквивалентны, справедливой будет запись:
Fн∆x=σ2L∆x или σ=Fн2L.
Определение 4
Исходя из этого, можно заявить, что коэффициент поверхностного натяжения σ может быть определен как модуль силы поверхностного натяжения, действующей на единицу длины линии, ограничивающей поверхность.
По причине воздействия сил поверхностного натяжения на капли жидкости и их действия внутри мыльных пузырей появляется некоторое избыточное давление Δp. При мысленном разрезании сферической капли с радиусом R на две равные части каждая из половин должна находиться в равновесии под действием приложенных к границе разреза длиной 2πR и сил избыточного давления, действующих на площадь πR2 сечения (рис. 3.5.4) сил поверхностного натяжения. Условие равновесия может быть записано в следующем виде:
σ2πR=∆pπR2.
Исходя из этого, можно заявить, что избыточное давление внутри капли эквивалентно:
∆p=2σR(капля жидкости).
Рисунок 3.5.4.Сечение сферической капли жидкости.
Из-за того, что пленка обладает двумя поверхностями, величина избыточного давления внутри мыльного пузыря в два раза выше, чем в капле:
∆p=4σR(мыльный пузырь).
Пренебрегая взаимодействием с молекулами газа, можно сказать, что поблизости с границей между твердым телом, жидкостью и газом форма свободной поверхности жидкости зависима от сил взаимодействия молекул жидкости с молекулами твердого тела.
Определение 5
В случае, когда данные силы превышают силы взаимодействия между молекулами жидкости, жидкость смачивает поверхность твердого тела. В таком случае жидкость подходит к поверхности твердого тела под некоторым характерным для данной пары жидкость – твердое тело острым углом θ. Такой угол носит название краевого угла.
Краевой угол θ является тупым (рисунок 3.5.5), в случае, если силы взаимодействия между молекулами жидкости превосходят силы их взаимодействия с молекулами твердого тела. В подобном случае можно сказать, что поверхность твердого тела не смачивается жидкостью. В условиях полного смачивания θ=0, полного несмачивания θ=180°.
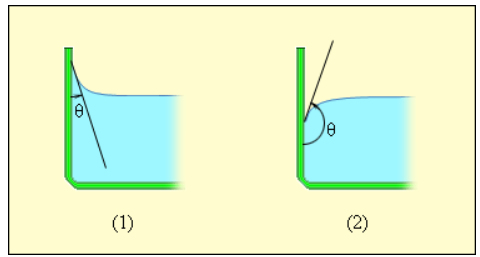
Рисунок 3.5.5. Краевые углы смачивающей (1) и несмачивающей (2) жидкостей.
Капиллярные явления
Определение 6
Капиллярными явлениями называют процесс подъема или опускания жидкости в трубках малого диаметра, другими словами, в капиллярах.
Смачивающие жидкости поднимаются по капиллярам, несмачивающие – опускаются. На рисунке 3.5.6 проиллюстрирована опущенная нижним концом в смачивающую жидкость плотности ρ капиллярная трубка, обладающая некоторым радиусом r. При этом верхний конец капилляра является открытым. Подъем жидкости в капилляре будет происходить до тех пор, пока сила тяжести Fт→, оказывающая воздействие на столб жидкости в капилляре, не станет эквивалентна по модулю результирующей Fндействующих вдоль границы соприкосновения жидкости с поверхностью капилляра сил поверхностного натяжения: Fт=Fн, где Fт=mg=ρhπr2g, Fн=σ2πr cos θ.
Из этого следует:
h=2σ cos θρgr.
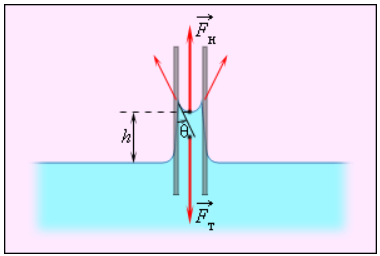
Рисунок 3.5.6. Подъем смачивающей жидкости в капилляре.
При полном смачивании θ=0, cos θ=1. В таком случае:
h=2σρgr.
При полном несмачивании θ=180°, cos θ=–1 и, соответственно, h<0. Уровень несмачивающей жидкости в капилляре опускается ниже уровня жидкости в сосуде, в которую опущен капилляр.
Вода почти полностью смачивает чистую поверхность стекла. Ртуть же, строго наоборот, полностью не смачивает стеклянную поверхность. По этой причине уровень ртути в стеклянном капилляре опускается ниже, чем уровень в сосуде.
Источник
Лекция 11.Характеристика жидкого состояния вещества. Поверхностный слой жидкости. Энергия поверхностного слоя. Явления на границе жидкости с твердым телом. Капиллярные явления.
ХАРАКТЕРИСТИКА ЖИДКОГО СОСТОЯНИЯ ВЕЩЕСТВА
Жидкость — это агрегатное состояние вещества, промежуточное между газообразным и твердым.
Вещество в жидком состоянии сохраняет свой объем, но принимает форму сосуда, в котором оно находится Сохранение объема у жидкости доказывает, что между ее молекулами действуют силы притяжения.
Если вокруг молекулы жидкости описать сферу молекулярного действия, то внутри этой сферы окажутся центры многих других молекул, которые будут взаимодействовать с нашей молекулой. Эти силы взаимодействия удерживают молекулу жидкости около ее временного положения равновесия примерно в течение 10-12-10-10 с, после чего она перескакивает в новое временное положение равновесия приблизительно на расстояние своего диаметра. Молекулы жидкости между перескоками совершают колебательное движение около временного положения равновесия.
Время между двумя перескоками молекулы из одного положения в другое называется временем оседлой жизни.
Это время зависит от вида жидкости и от температуры. При нагревании жидкости среднее время оседлой жизни молекул уменьшается.
Итак, в небольшом объеме жидкости наблюдается упорядоченное расположение ее молекул, а в большом объеме оно оказывается хаотическим. В этом смысле говорят, что в жидкости существует ближний порядок в расположении молекул и отсутствует дальний порядок. Такое строение жидкости называют квазикристаллическим (кристаллоподобным).
СВОЙСТВА ЖИДКОСТИ
1.Если время действия силы на жидкость мало, то жидкость проявляет упругие свойства. Например, при резком ударе палкой о поверхность воды палка может вылететь из руки или сломаться; камень можно бросить так, что он при ударе о поверхность воды отскакивает от нее, и лишь совершив несколько скачков, тонет в воде.
2. Если же время воздействия на жидкость велико, то вместо упругости проявляется текучесть жидкости. Например, рука легко проникает внутрь воды.
3. При кратковременном действии силы на струю жидкости последняя обнаруживает хрупкость. Прочность жидкости нд разрыв хотя и меньше, чем у твердых веществ, но мало уступает им по величине. Для воды она составляет 2,5-107 Н/м2.
4.Сжимаемость жидкости тоже очень мала, хотя она и больше, чем у этих же веществ в твердом состоянии. Например, при увеличении давления на 1 атм объем воды уменьшается на 50 миллионных долей.
Разрывы внутри жидкости, в которой нет посторонних веществ, например воздуха, могут получаться только при интенсивном воздействии на жидкость, например при вращении гребных винтов в воде, при распространении в жидкости ультразвуковых волн . Такого рода пустоты внутри жидкости долго существовать не могут и резко захлопываются, т. е. исчезают. Это явление называют кавитацией (от греческого «кавитас» – полость). Оно служит причиной быстрого износа гребных винтов.
ПОВЕРХНОСТНЫЙ СЛОЙ ЖИДКОСТИ
Среднее значение равнодействующей молекулярных сил притяжения, приложенных к молекуле, которая находится внутри жидкости (рис. 2), близко к нулю. Случайные флуктуации этой равнодействующей заставляют молекулу совершать лишь хаотическое движение внутри жидкости. Несколько иначе обстоит дело с молекулами, находящимися в поверхностном слое жидкости.
Опишем вокруг молекул сферы молекулярного действия радиусом R(порядка 10-8 м). Тогда для верхней молекулы в нижней полусфере окажется много молекул, а в верхней – значительно меньше, так как снизу находится жидкость, а сверху – пар и воздух. Поэтому для верхней молекулы равнодействующая молекулярных сил притяжения в нижней полусфере много больше равнодействующей молекулярных сил в верхней полусфере.
Таким образом, все молекулы жидкости, находящиеся в поверхностном слое толщиной, равной радиусу молекулярного действия, втягиваются внутрь жидкости. Но пространство внутри жидкости занято другими молекулами, поэтому поверхностный слой создает давление на жидкость, которое называют молекулярным давлением.
Силы, действующие в горизонтальной плоскости, стягивают поверхность жидкости. Они называются силами поверхностного натяжения
Поверхностное натяжение — физическая величина, равная отношению силы F поверхностного натяжения, приложенной к границе поверхностного слоя жидкости и направленной по касательной к поверхности, к длине l этой границы:
Единица поверхностного натяжения – ньютон на метр (Н/м).
Поверхностное натяжение различно для разных жидкостей и зависит от температуры.
Обычно поверхностное натяжение уменьшается с возрастанием температуры и при критической температуре, когда плотность жидкости и пара одинаковы, поверхностное натяжение жидкости равно нулю.
Вещества, которые уменьшают поверхностное натяжение, называют поврхностно – активными (спирт, мыло, стиральный порошок)
Чтобы увеличить площадь поверхности жидкости требуется выполнить работу против поверхностного натяжения.
Имеется другое определение коэффициента поверхностного натяжения — энергетическое. Оно исходит из того, что если площадь поверхности жидкости увеличивается, то некоторое количество молекул из ее объема поднимается на слой поверхности. С этой целью внешние силы совершают работу против молекулярных сил сцепления молекул. Величина данной работы будет пропорциональна изменению площади поверхности жидкости:
Коэффициент пропорциональности σ и называется поверхностным натяжением жидкости.
Выведем единицу поверхностного, натяжения а в СИ: о=1 Дж/1 м2= 1 Дж/м2.
Источник
Монета, лежащая на поверхности воды благодаря силе поверхностного натяжения
Пове́рхностное натяже́ние — термодинамическая характеристика поверхности раздела двух находящихся в равновесии фаз, определяемая работой обратимого изотермокинетического образования единицы площади этой поверхности раздела при условии, что температура, объём системы и химические потенциалы всех компонентов в обеих фазах остаются постоянными.
Поверхностное натяжение имеет двойной физический смысл — энергетический (термодинамический) и силовой (механический). Энергетическое (термодинамическое) определение: поверхностное натяжение — это удельная работа увеличения поверхности при её растяжении при условии постоянства температуры. Силовое (механическое) определение: поверхностное натяжение — это сила, действующая на единицу длины линии, которая ограничивает поверхность жидкости[1].
Сила поверхностного натяжения направлена по касательной к поверхности жидкости, перпендикулярно к участку контура, на который она действует и пропорциональна длине этого участка. Коэффициент пропорциональности
— сила, приходящаяся на единицу длины контура — называется коэффициентом поверхностного натяжения. В СИ он измеряется в ньютонах на метр.
Но более правильно дать определение поверхностному натяжению, как энергии в джоулях на разрыв единицы поверхности (м²). В этом случае появляется ясный физический смысл понятия поверхностного натяжения.
В 1983 году было доказано теоретически и подтверждено данными из справочников[2], что понятие поверхностного натяжения жидкости однозначно является частью понятия внутренней энергии (хотя и специфической: для симметричных молекул близких по форме к шарообразным). Приведенные в этой журнальной статье формулы позволяют для некоторых веществ теоретически рассчитывать значения поверхностного натяжения жидкости по другим физико-химическим свойствам, например, по теплоте парообразования или по внутренней энергии[3][4]).
В 1985 году аналогичный взгляд на физическую природу поверхностного натяжения как части внутренней энергии при решении другой физической задачи был опубликован В. Вайскопфом (Victor Frederick Weisskopf) в США[5].
Поверхностное натяжение возникает на границе газообразных, жидких и твёрдых тел. Обычно под термином «поверхностное натяжение» имеется в виду поверхностное натяжение жидких тел на границе жидкость — газ. В случае жидкой поверхности раздела поверхностное натяжение правомерно также рассматривать как силу, действующую на единицу длины контура поверхности и стремящуюся сократить поверхность до минимума при заданных объёмах фаз.
Прибор для измерения поверхностного натяжения называется тензиометр.
Проявления[править | править код]
Водомерка на поверхности воды.
Так как увеличение площади поверхности раздела жидкость — газ требует совершения работы, жидкость «стремится» уменьшить площадь своей поверхности:
- в невесомости порция жидкости принимает сферическую форму (сфера имеет наименьшую площадь поверхности среди всех тел одинакового объёма). То же самое происходит с каплей жидкости, помещаемой внутрь другой, несмешивающейся жидкости с первой жидкостью той же плотности (опыт Плато).
- ламинарная струя воды образует цилиндр, который затем разбивается на шаровидные капли из-за неустойчивости Рэлея — Плато.
- небольшие предметы со средней плотностью большей плотности жидкости способны «плавать» на поверхности жидкости, так как их вес оказывается уравновешенным силой поверхностного натяжения.
- некоторые насекомые (например, водомерки) способны передвигаться по воде, удерживаясь на её поверхности за счёт сил поверхностного натяжения.
- На многих поверхностях, именуемых несмачиваемыми (гидрофобными), вода (или другая жидкость) собирается в капли.
Теория[править | править код]
Пояснение возникновения силы поверхностного натяжения. Молекулы на границе раздела испытывают силы, стремящиеся втянуть их в жидкость, так как со стороны газа на них не действуют силы притяжения.
Площадь поверхности[править | править код]
Поверхность жидкости обладает свободной энергией:
где — коэффициент поверхностного натяжения,
— полная площадь поверхности жидкости[6].
Так как свободная энергия изолированной системы стремится к минимуму, то жидкость (в отсутствие внешних полей) стремится принять форму, имеющую минимальную площадь поверхности. Таким образом задача о форме жидкости сводится к изопериметрической задаче при заданных дополнительных условиях (начальное распределение, объём и т. п.). Свободная капля стремится принять форму шара, однако при более сложных начальных условиях задача о форме поверхности жидкости становится математически исключительно сложной.
Формула Лапласа[править | править код]
Рассмотрим тонкую жидкую плёнку, толщиной которой можно пренебречь. Стремясь минимизировать свою свободную энергию, плёнка создаёт разность давления с разных сторон. Этим объясняется образование мыльных пузырей: плёнка сжимается до тех пор, пока давление внутри пузыря не будет превышать атмосферное на величину добавочного давления поверхностного натяжения плёнки. Добавочное давление в точке поверхности зависит от средней кривизны в этой точке и задаётся формулой Лапласа:
Здесь — радиусы главных кривизн в точке. Они имеют одинаковый знак, если соответствующие центры кривизны лежат по одну сторону от касательной плоскости в точке, и разный знак — если по разную сторону. Например, для сферы центры кривизны в любой точке поверхности совпадают с центром сферы, поэтому:
Для случая поверхности кругового цилиндра радиуса имеем:
Так как должна быть непрерывной функцией на поверхности плёнки, поэтому выбор «положительной» стороны плёнки в одной точке локально однозначно задаёт положительную сторону поверхности в достаточно близких её точках.
Из формулы Лапласа следует, что свободная мыльная плёнка, натянутая на рамку произвольной формы и не образующая пузырей, будет иметь среднюю кривизну, равную 0.
Зависимость от температуры[править | править код]
С увеличением температуры величина поверхностного натяжения уменьшается и равна нулю при критической температуре. Наиболее известная эмпирическая зависимость поверхностного натяжения от температуры была предложена Лорандом Этвёшом, так называемое правило Этвёша. В настоящее время получен вывод теоретической зависимости поверхностного натяжения от температуры в области до критических температур, подтверждающей правило Этвёша[7].
Способы определения[править | править код]
Способы определения поверхностного натяжения делятся на статические и динамические. В статических методах поверхностное натяжение определяется у сформировавшейся поверхности, находящейся в равновесии. Динамические методы связаны с разрушением поверхностного слоя. В случае измерения поверхностного натяжения растворов (особенно полимеров или ПАВ) следует пользоваться статическими методами. В ряде случаев равновесие на поверхности может наступать в течение нескольких часов (например, в случае концентрированных растворов полимеров с высокой вязкостью). Динамические методы могут быть применены для определения равновесного поверхностного натяжения и динамического поверхностного натяжения.
Например, для раствора мыла после перемешивания поверхностное натяжение 58 мДж/м², а после отстаивания — 35 мДж/м². То есть поверхностное натяжение меняется.
До установления равновесного оно будет динамическое.
Статические методы:
- Метод измерения высоты поднятия мениска в капилляре.
- Метод Вильгельми.
- Метод лежачей капли.
- Метод определения по форме висячей капли.
- Метод вращающейся капли.
Динамические методы:
- Метод дю Нуи (метод отрыва кольца).
- Сталагмометрический, или метод счета капель.
- Метод максимального давления пузырька.
- Метод осциллирующей струи.
- Метод стоячих волн.
- Метод бегущих волн.
Методы[править | править код]
Полностью стандартизованные методы измерений описываются в соответствующих ASTM, ГОСТ и т. д.
Метод вращающейся капли[править | править код]
Сущностью метода является измерение диаметра капли жидкости, вращающейся в более тяжелой жидкости[8]. Этот способ измерения годится для измерения низких или сверхнизких значений межфазного натяжения. Он широко применяется для микроэмульсий, измерения эффективности поверхностно-активных веществ (ПАВ) в нефтедобыче, а также для определения адсорбционных свойств.
Метод Дю Нуи (метод отрыва кольца)[править | править код]
Метод является классическим. Сущность метода вытекает из названия. Кольцо из платиновой проволоки плоскость которого параллельна поверхности жидкости медленно поднимают из жидкости, смачивающей его, усилие в момент отрыва кольца от поверхности и есть сила поверхностного натяжения и может быть пересчитано в поверхностную энергию. Метод подходит для измерения поверхностного натяжения ПАВ, трансформаторных масел и т. д.
Метод капиллярных волн[править | править код]
При возмущении жидкости колеблющейся пластиной, лежащей на её поверхности, по поверхности жидкости распространяются капиллярные волны. Если осветить кювету с жидкостью импульсным источником света (стробоскопом) с частотой вспышек равной частоте колебания пластины возмущения, то будет наблюдаться зрительно неподвижная волновая картина. По измеренной длине волны можно рассчитать величину поверхностного натяжения по формуле:
где — поверхностное натяжение;
— плотность жидкости;
— длина волны;
— частота колебания пластины;
— ускорение свободного падения.
Поверхностное натяжение некоторых жидкостей на границе с воздухом[править | править код]
| Вещество | Температура °C | Поверхностное натяжение(10−3 Н/м) |
|---|---|---|
| Хлорид натрия 6 M водный раствор | 20 | 82,55 |
| Хлорид натрия | 801 | 115 |
| Глицерин | 30 | 64,7 |
| Олово | 400 | 518 |
| Азотная кислота 70 % | 20 | 59,4 |
| Анилин | 20 | 42,9 |
| Ацетон | 20 | 23,7 |
| Бензол | 20 | 29,0 |
| Вода | 20 | 72,86 |
| Глицерин | 20 | 59,4 |
| Нефть | 20 | 26 |
| Ртуть | 20 | 486,5 |
| Серная кислота 85 % | 20 | 57,4 |
| Спирт этиловый | 20 | 22,8 |
| Уксусная кислота | 20 | 27,8 |
| Эфир этиловый | 20 | 16,9 |
| Раствор мыла | 20 | 43 |
Проявления[править | править код]
Мыльный пузырь
Маргаритка
На фотографии виден эффект, получивший название «слёзы вина»
Капля воды на листе
Вода набегает на сухую поверхность асфальта
См. также[править | править код]
- Тензиометр
- Формула Жюрена
Ссылки[править | править код]
- [www.xumuk.ru/colloidchem/19.html Методы определения поверхностного натяжения]
- Видео о физической природе поверхностного натяжения жидкости как части внутренней энергии (рус.)
Примечания[править | править код]
- ↑ Сумм Б. Д. Основы коллоидной химии
- ↑ (Cтатья: Журнал физической химии. 1983, № 10, с. 2528—2530)
- ↑ Хайдаров Г. Г., Хайдаров А. Г., Машек А. Ч. Физическая природа поверхностного натяжения жидкости // Вестник Санкт-Петербургского университета. Серия 4 (Физика, химия) 2011. Выпуск 1. с.3-8. (недоступная ссылка). Дата обращения 16 февраля 2014. Архивировано 22 февраля 2014 года.
- ↑ Хайдаров Г. Г., Хайдаров А. Г., Машек А. Ч., Майоров Е. Е. Влияние температуры на поверхностное натяжения // Вестник Санкт-Петербургского университета. Серия 4 (Физика, химия). 2012. Выпуск 1. с.24-28. (недоступная ссылка). Дата обращения 16 февраля 2014. Архивировано 22 февраля 2014 года.
- ↑ Weisskopf V. F. American Journal of Physics 53 (1985) 19-20.; V. F. Weisskopf, American Journal of Physics 53 (1985) 618—619.
- ↑ Обратите внимание, что плёнка, вроде стенки мыльного пузыря, имеет две стороны, так что площадь поверхности жидкости в два раза больше площади плёнки.
- ↑ Журнал «Вестник Санкт-Петербургского университета», 2012, вып. 1, с. 24—28
- ↑ Тензиометр SITE100
Некоторые внешние ссылки в этой статье ведут на сайты, занесённые в спам-лист. Эти сайты могут нарушать авторские права, быть признаны неавторитетными источниками или по другим причинам быть запрещены в Википедии. Редакторам следует заменить такие ссылки ссылками на соответствующие правилам сайты или библиографическими ссылками на печатные источники либо удалить их (возможно, вместе с подтверждаемым ими содержимым). Список проблемных доменов |
Источник
